Полином Лежандра — это… Что такое Полином Лежандра?
- Полином Лежандра
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде
Они также могут быть вычислены по рекуррентной формуле
Присоединённые многочлены Лежандра определяются по формуле
которую также можно представить в виде
При m = 0 функция совпадает с Pn.
Примеры
Первые четыре многочлена Лежандра равны:
- P
- P1(x) = x
Свойства
- При каждом m > 0 система присоединённых функций Лежандра полна в L2( − 1,1).
- В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
- и ,
где — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
- P
Wikimedia Foundation. 2010.
- Полином Лагранжа
- Полином Чебышева
Смотреть что такое «Полином Лежандра» в других словарях:
полином Лежандра — Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. Legendre polynomial vok. Legendresches Polynom, n rus. многочлен Лежандра, m; полином Лежандра, m pranc. polynôme de Legendre, m … Fizikos terminų žodynas
присоединённый полином Лежандра — prijungtinis Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. associated Legendre polynomial vok. Legendresches zugeordnetes Polynom, n; zugeordnetes Legendresches Polynom, n rus. присоединённый многочлен Лежандра, m;… … Fizikos terminų žodynas
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
многочлен Лежандра — Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. Legendre polynomial vok. Legendresches Polynom, n rus. многочлен Лежандра, m; полином Лежандра, m pranc. polynôme de Legendre, m … Fizikos terminų žodynas
присоединённый многочлен Лежандра — prijungtinis Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. associated Legendre polynomial vok. Legendresches zugeordnetes Polynom, n; zugeordnetes Legendresches Polynom, n rus. присоединённый многочлен Лежандра, m;… … Fizikos terminų žodynas
РАССЕЯНИЕ МИКРОЧАСТИЦ — процесс столкновения ч ц, в результате к рого меняются импульсы ч ц (у п р у г о е р а с с е я н и е) или наряду с изменением импульсов меняются также внутр. состояния ч ц (к в а з и у п р у г и е п р о ц е с с ы) либо образуются др. ч цы (н е у… … Физическая энциклопедия
СФЕРИЧЕСКИЕ ФУНКЦИИ — (сферические гармоники) спец. функции, возникающие, напр., при отыскании ограниченных решений ур ния Лапласа Du = 0 в сферич. координатах (r, q, j) методом разделения переменных. Введены в кон. 18 в. А. Лежандром и П. Лапласом. Полагая и = и(r,q … Физическая энциклопедия
Юпитер — У этого термина существуют и другие значения, см. Юпитер (значения). Юпитер … Википедия
Гипергеометрическая функция — (функция Гаусса) определяется внутри круга как сумма гипергеометрического ряда а при как её аналитическое продолжение. Она является решением линейного обыкновенного дифференциального уравнения (ОДУ) второго порядка называемого… … Википедия
Legendre polynomial
dic.academic.ru
Многочлены Лежандра — это… Что такое Многочлены Лежандра?
Многочлен Лежа́ндра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Определение
Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода
Рассмотрим дифференциальное уравнение вида
| (УравнПолЛеж) |
где — комплексная переменная. Решения этого уравнения при целых имеют вид многочленов, называемых многочленами Лежандра
. Полином Лежандра степени можно представить через формулу Родрига в виде[1]Часто вместо записывают косинус полярного угла:
Уравнение (УравнПолЛеж) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра
| (УравнЛеж) |
где , — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при (в частности, при действительных ) или когда действительная часть числа больше единицы. Его решения называют присоединёнными функциями Лежандра или шаровыми функциями. Подстановка вида в (УравнЛеж) даёт уравнение Гаусса, решение которого в области принимает вид
где F — гипергеометрическая функция. Подстановка в (УравнЛеж) приводит к решению вида
определённым на . Функции и называют функциями Лежандра первого
Справедливы соотношения[3]
и
Формулы с
- Многочлены Лежандра также определяются по следующим формулам:
- , если ;
- , если .
Рекуррентная формула
Формулы с разложениями
- Многочлены Лежандра также определяются следующими разложениями:
для ± :
и для ± :
Следовательно,
Присоединённые многочлены Лежандра
- Присоединённые многочлены Лежандра определяются по формуле:
которую также можно представить в виде:
При функция совпадает с .
Матрица функции многочлена Лежандра
Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны , где .
Примеры
 Первые 6 многочленов Лежандра. Первые многочлены Лежандра равны:
Первые 6 многочленов Лежандра. Первые многочлены Лежандра равны:Поскольку , то
Свойства
- Что также можно записать как:
где — символ Кронекера.
- Для , норма равна:
- Нормированная функция многочленов Лежандра связана с нормой следующим соотношением:
- — четная функция;
- — нечетная функция.
Ряды многочленов Лежандра
Разложение липшицевой функции в ряд многочленов Лежандра
Липшицевая функция является функцией со свойством:
- , где .
Эта функция разлагается в ряд многочленов Лежандра.
Пусть — пространство непрерывных отображений на отрезке , и .
Пусть
тогда удовлетворяет следующему условию:
Пусть и удовлетворяет следующим условиям:
- , где
Липшецевую функцию можно записать следующим образом:
Разложение голоморфной функции
Всякая функция f, голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:
Теорема сложения
Для величин, удовлетворяющих условиям , , , — действительное число, можно записать теорему сложения для полиномов Лежандра первого рода:[4]
или, в альтернативной форме через гамма-функцию:
Для полиномов Лежандра второго рода теорема сложения выглядит как[5]
при условиях , , ,
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра ) естественно возникают в теории потенциала.
Шаровые функции — это функции (в сферических координатах ) вида (с точностью до константы)
- и
где — присоединённые многочлены Лежандра;
а точнее вида , где — сферические функции.
Шаровые функции удовлетворяют уравнению Лапласа всюду в .
Примечания
- ↑ Градштейн, Рыжик, 1963, с. 1039
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 126—127
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 140
- ↑ Градштейн, Рыжик, 1963, с. 1027
- ↑ Градштейн, Рыжик, 1963, с. 1028
Литература
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
- Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
- Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
- Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
- Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
dic.academic.ru
Присоединённые многочлены Лежандра — это… Что такое Присоединённые многочлены Лежандра?
- Присоединённые многочлены Лежандра
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде
Они также могут быть вычислены по рекуррентной формуле
Присоединённые многочлены Лежандра определяются по формуле
которую также можно представить в виде
При m = 0 функция совпадает с Pn.
Примеры
Первые четыре многочлена Лежандра равны:
- P0(x) = 1
- P1(x) = x
Свойства
- При каждом m > 0 система присоединённых функций Лежандра полна в L2( − 1,1).
- В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
- и ,
где — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation. 2010.
- Присоединённое представление лиевой алгебры
- Присосконоги
Смотреть что такое «Присоединённые многочлены Лежандра» в других словарях:
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлен Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полином Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полиномы Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Функция Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
C++ Technical Report 1 — (TR1) является общим названием для стандарта ISO / IEC TR 19768, библиотеки расширений C++ это документ с предложением дополнений в стандарт библиотеки С++. Дополнения включают регулярные выражения, умные указатели, хэш таблицы, и… … Википедия
Сферические функции — представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями … Википедия
dic.academic.ru
Реферат Многочлены Лежандра
скачатьРеферат на тему:
План:
- Введение
- 1 Определение
- 1.1 Формула Родрига
- 1.2 Формулы с Σ
- 1.3 Рекуррентная формула
- 1.4 Формулы с разложениями
- 1.5 Присоединённые многочлены Лежандра
- 2 Матрица функции многочлена Лежандра
- 3 Примеры
- 4 Свойства
- 5 Ряды многочленов Лежандра
- 5.1 Разложение липшицевой функции в ряд многочленов Лежандра
- 5.2 Разложение голоморфной функции
- 6 Функции Лежандра Литература
Введение
Многочлены Лежандра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
1. Определение
1.1. Формула Родрига
- Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде:
1.2. Формулы с Σ
- Многочлены Лежандра также определяются по следующим формулам:
- , если ;
- , если .
1.3. Рекуррентная формула
- Они также могут быть вычислены по рекуррентной формуле:
1.4. Формулы с разложениями
- Многочлены Лежандра также определяются следующими разложениями:
для ± :
и для ± :
Следовательно,
1.5. Присоединённые многочлены Лежандра
- Присоединённые многочлены Лежандра определяются по формуле:
которую также можно представить в виде:
При m = 0 функция совпадает с Pn.
2. Матрица функции многочлена Лежандра
Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны k(k + 1), где .
3. Примеры
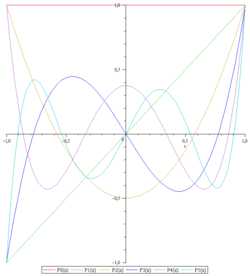
Первые 6 многочленов Лежандра.
Первые многочлены Лежандра равны:
Поскольку Pn(1) = 1,
4. Свойства
- Присоединённые многочлены Лежандра являются решениями дифференциального уравнения
- Что также можно записать как:
- Производящая функция для многочленов Лежандра равна:
- Условие ортогональности этих полиномов на отрезке :
где δkl — символ Кронекера.
- Для , норма Pn равна:
- Нормированная функция многочленов Лежандра связана с нормой Pn следующим соотношением:
- При каждом m > 0 система присоединённых функций Лежандра полна в .
- В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
- — четная функция;
- — нечетная функция.
5. Ряды многочленов Лежандра
5.1. Разложение липшицевой функции в ряд многочленов Лежандра
Липшицевая функция f является функцией со свойством:
- , где L > 0.
Эта функция разлагается в ряд многочленов Лежандра.
Пусть — пространство непрерывных отображений на отрезке , и .
Пусть
тогда удовлетворяет следующему условию:
Пусть и удовлетворяет следующим условиям:
- , где
Липшецевую функцию f можно записать следующим образом:
5.2. Разложение голоморфной функции
Всякая функция f, голоморфная внутри эллипса с фокусами -1 и +1, может быть представлена в виде ряда:
6. Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра ) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах ) вида
- и
где — присоединённые многочлены Лежандра.
Сферические функции удовлетворяют уравнению Лапласа всюду в и служат ортогональным базисом для функций.
Литература
- Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
- Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
- Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
wreferat.baza-referat.ru
1.4. Ортогональность полиномов Лежандра и их норма
Докажем что
полиномам Лежандра различных порядков
ортогональны на отрезке
.
Согласно общей теореме присоединенные
функции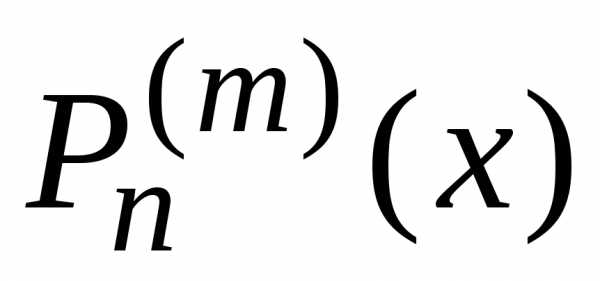 образуют ортогональную систему. Вычислим
норму
образуют ортогональную систему. Вычислим
норму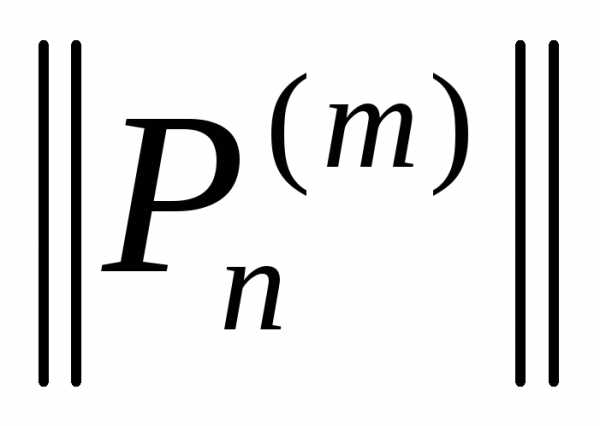 присоединенных функций. Попутно будет
доказана их ортогональность.
присоединенных функций. Попутно будет
доказана их ортогональность.
, (1)
, (2)
где
,.Домножим
(1) на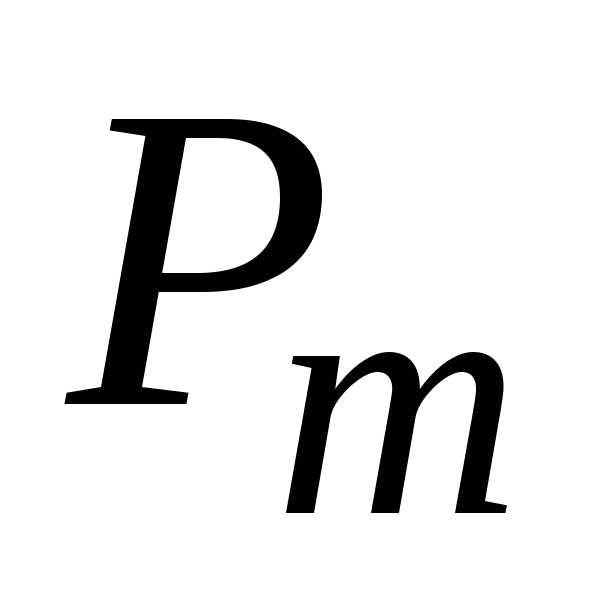 (x),
а (2) на
(x),
а (2) на 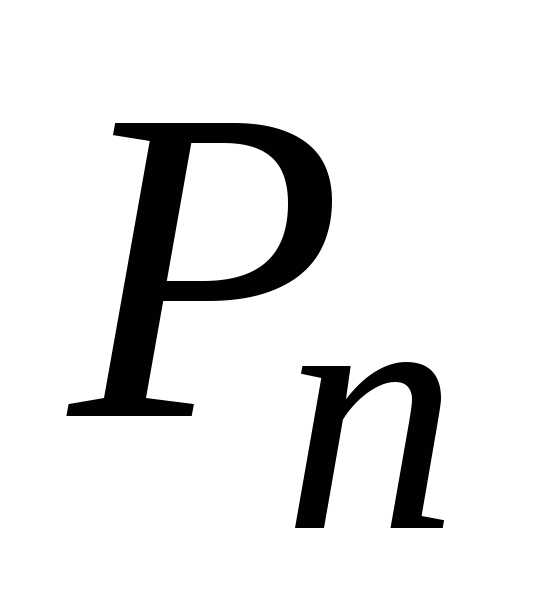 (x),
а затем вычтем (1) из (2):
(x),
а затем вычтем (1) из (2):
,
, (3)
Доказать
ортогональность если 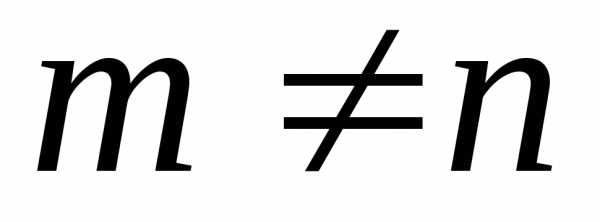 .
Если
.
Если 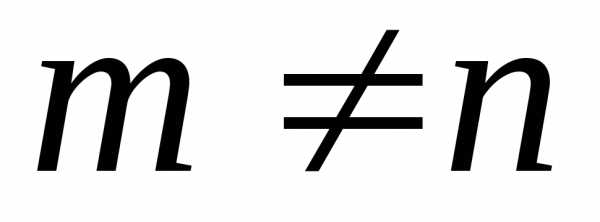 ,
то полиномы
Лежандра разных порядков ортогональны
между собой:
,
то полиномы
Лежандра разных порядков ортогональны
между собой:
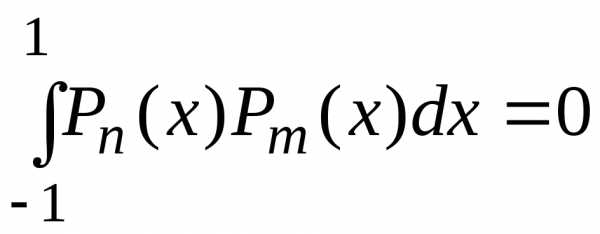
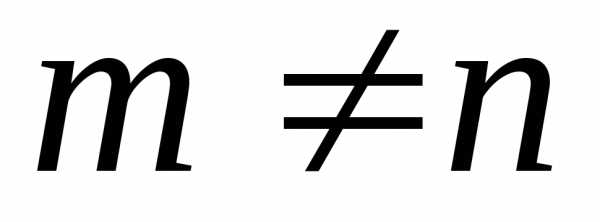 . (4)
. (4)
1.5. Норма полиномов Лежандра
Вычислим норму
полиномов Лежандра 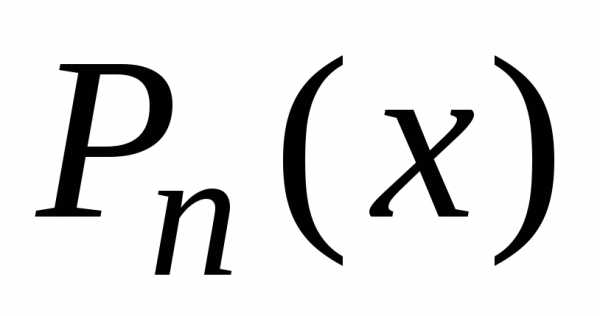
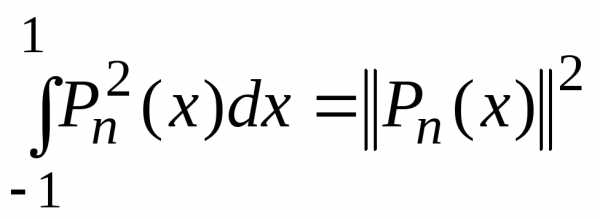
(5)
Применим рекуррентную
формулу (11) (§1.1) дважды: сначала выразим
из нее (предварительно заменив в (11) n+1 на n) 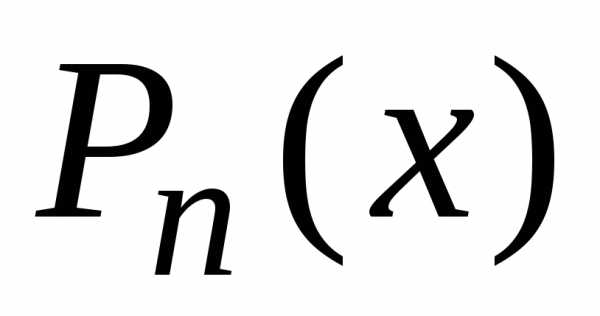 через
через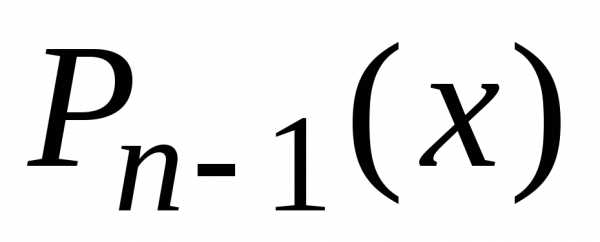 и
и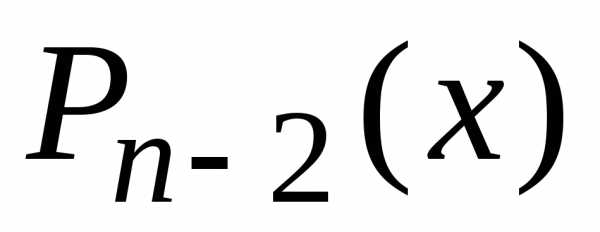 ,
а затем
,
а затем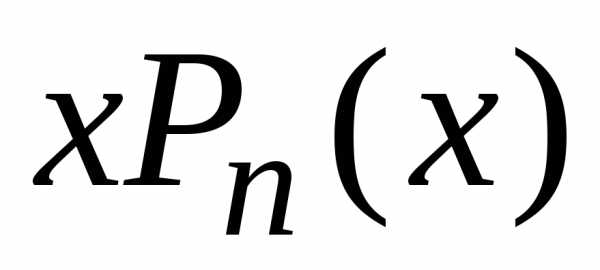 через
через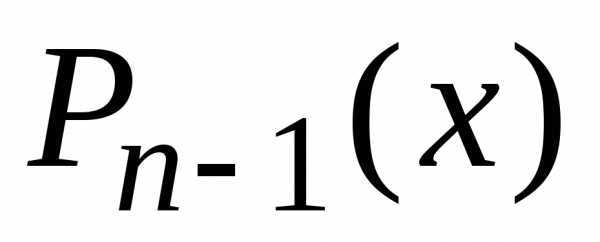 и
и .
Учитывая ортогональность полиномов
.
Учитывая ортогональность полиномов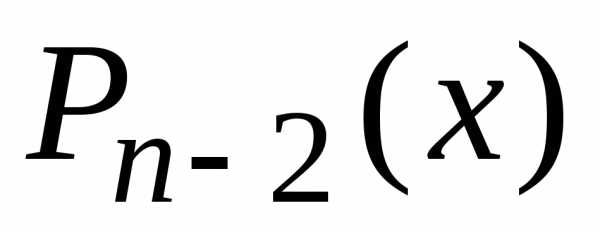 ,
,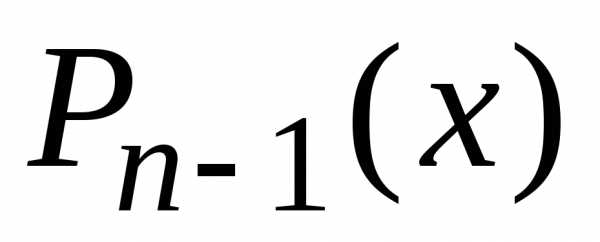 ,
,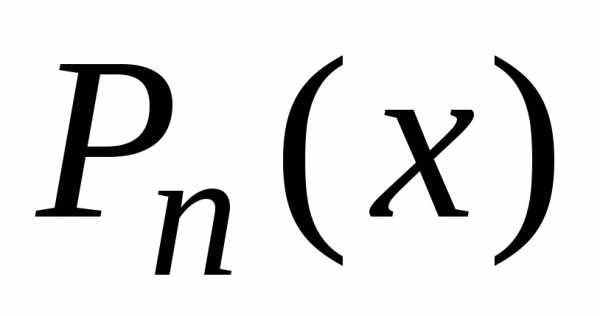 ,
получим:
,
получим:
(6)
Рекуррентная формула для нормы:
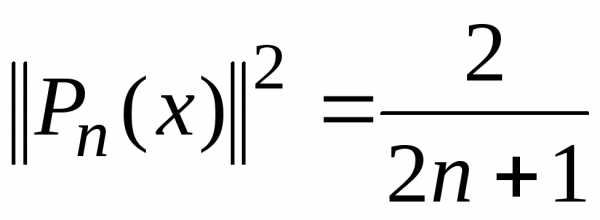
(7)
Полиномы Лежандра образуют замкнутую систему функций. Поэтому произвольная функция может быть разложена в ряд
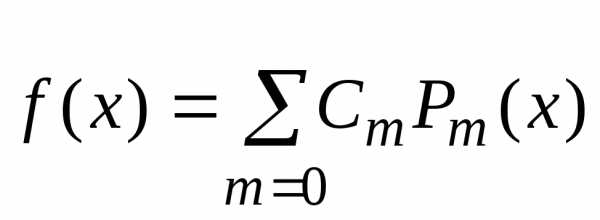 ,
,
который
домножим на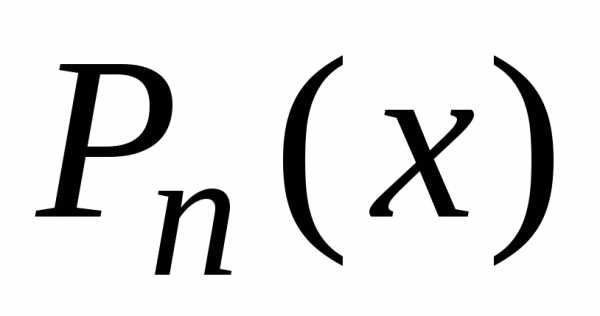 и проинтегрируем:
и проинтегрируем:
.
Система ортогональных функций называют замкнутой если не существует непрерывных функции тождественно равных 0 и ортогональных ко всем функциям системы.
Система ортогональных
функций 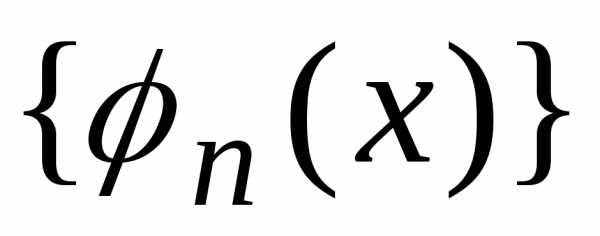 называется полной в (a,b)
если любую непрерывную функцию можно
аппроксимировать с любой степенью
точности при помощи линейной комбинации
называется полной в (a,b)
если любую непрерывную функцию можно
аппроксимировать с любой степенью
точности при помощи линейной комбинации 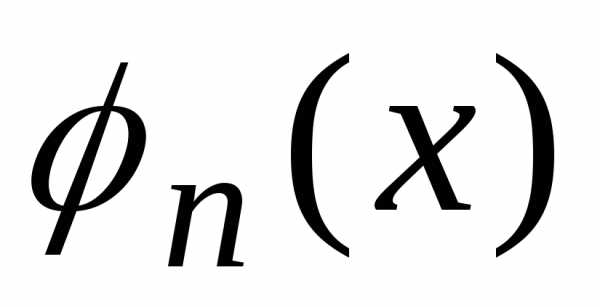 .
.
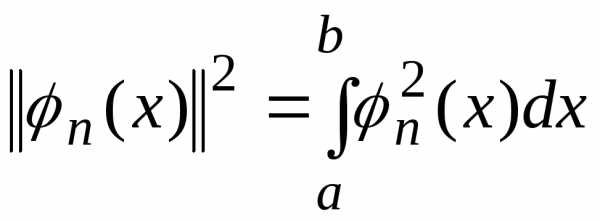
Замкнутость есть условие полноты, а полнота есть следствие замкнутости.
Упражнения
Получить полиномы Лежандра, используя производящую функцию, для n=0,1,2.
Получить полиномы Лежандра, используя формулу Родрига, для n=0,1,2,3,4,5.
Получить полиномы Лежандра, используя рекуррентную формулу для коэффициентов, для n=0,1,2,3,4,5,6.
Ответ:
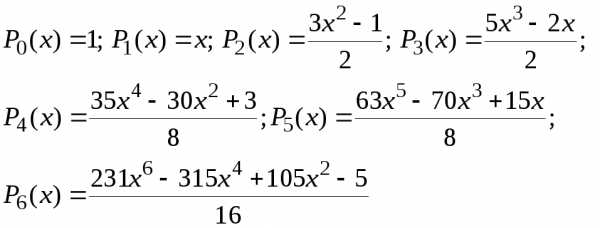
Построить и исследовать (найти точки перегибов, максимумов и минимумов) полиномов Лежандра для n=0,1,2,3,4,5.
Получить присоединенные функции Лежандра для n, m=0,1,2,3,4. Выразить данные функции через тригонометрические функции.
Получить сферические функции для l=0,1,2.
Показать, что сферические функции ортонормированны. Ограничиться l=0,1.
Выполнить визуализацию сферических функций.
Ответ:
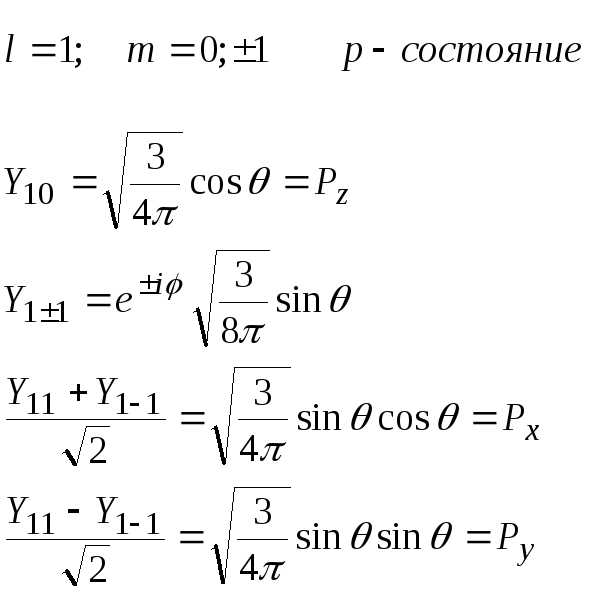

§2 Присоединенные функции Лежандра
2.1. Присоединенные функции
Рассмотрим следующую задачу:
Найдем собственные значения и собственные функции следующего уравнения
(1)
-1<x<1 при условии ограниченности
(2)
Будем искать решение в виде:
(3)
Подставим (3) в (1), найдем
,
,
. (4)
Это же уравнение
получается для производной 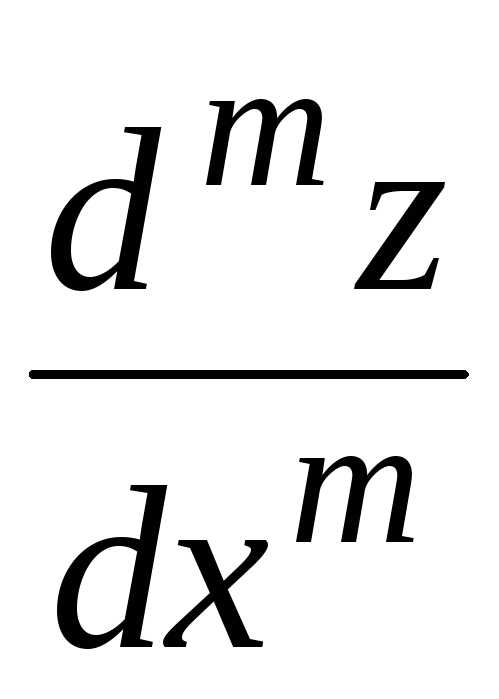 решения
уравнения Лежандра (17) из §1, если
продифференцироватьm раз.
решения
уравнения Лежандра (17) из §1, если
продифференцироватьm раз.
, (4а)
,
Продифференцируем соотношение (4) n раз, тогда получим
,
,(5)
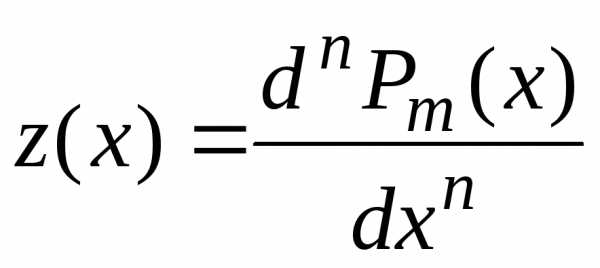 . (6)
. (6)
Нетривиальное и
ограниченное решение 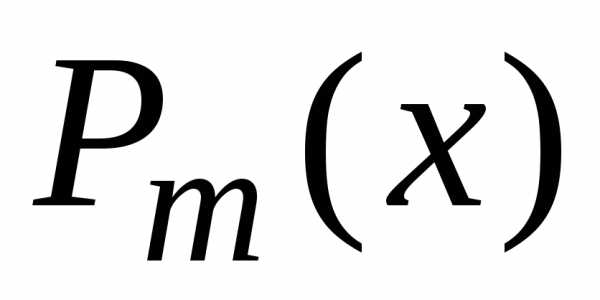 решении
уравнения Лежандра существует при
,
гдеm>0.
Решение
Соотношение
(6) является решением уравнения (3)
решении
уравнения Лежандра существует при
,
гдеm>0.
Решение
Соотношение
(6) является решением уравнения (3)
,
есть собственная
функция исходной задачи (1) для собственных
значений
,где
m-целые
числа (7). 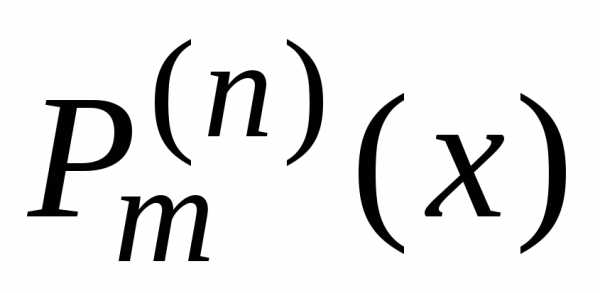 —
присоединенная функция Лежандра
—
присоединенная функция Лежандра
,
Если n=0, то
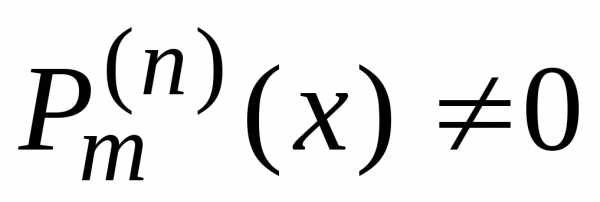 при
при 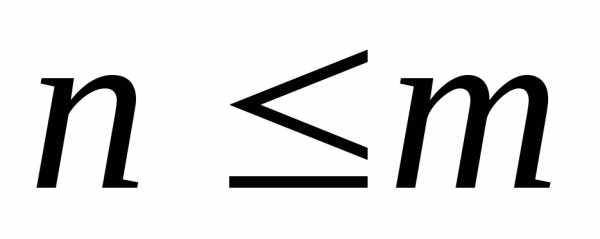 .
.
2.2. Норма присоединенной функции
Согласно общей
теоремы
присоединенные функции образуют
ортогональную систему. Вычислим норму 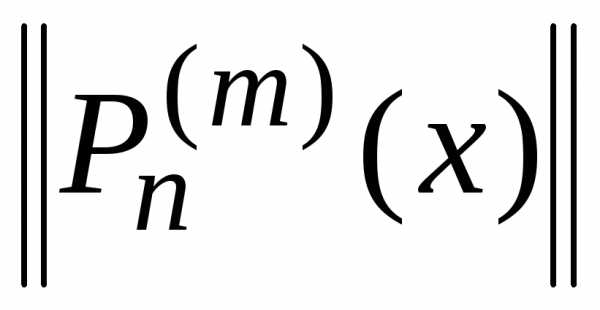 и докажем ортогональность
и докажем ортогональность
(8)
Уменьшим n на 1:
(9)
, (10)
Введем обозначение:
Подстановка обращается в нуль, а интеграл в силу (8) и (7) преобразуется к виду
,
, (11)
, (12)
Нетрудно показать, что
,
.
studfiles.net
Многочлены Лежандра — Википедия
Многочлен Лежа́ндра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов на отрезке в пространстве . Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода[править]
Рассмотрим дифференциальное уравнение вида
| (УравнПолЛеж) |
где — комплексная переменная. Решения этого уравнения при целых имеют вид многочленов, называемых многочленами Лежандра. Полином Лежандра степени можно представить через формулу Родрига в виде[1]
Часто вместо записывают косинус полярного угла:
Уравнение (УравнПолЛеж) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра
| (УравнЛеж) |
где , — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при (в частности, при действительных ) или когда действительная часть числа больше единицы. Его решения называют присоединёнными функциями Лежандра или шаровыми функциями. Подстановка вида в (УравнЛеж) даёт уравнение Гаусса, решение которого в области принимает вид
где F — гипергеометрическая функция. Подстановка в (УравнЛеж) приводит к решению вида
определённым на . Функции и называют функциями Лежандра первого и второго рода.[2]
Справедливы соотношения[3]
и
Выражение через суммы[править]
- Многочлены Лежандра также определяются по следующим формулам:
- , если ;
- , если .
Рекуррентная формула[править]
| (РекуррЛеж) |
- причем первые две функции имеют вид
Производная полинома Лежандра[править]
- Вычисляется по формуле[5]:
| (ПроизвЛеж) |
Корни полинома Лежандра[править]
- Вычисляются итеративно по методу Ньютона[5]:
- ,
- причем, начальное приближение для i-го корня (i = 1, 2, …, n) берется по формуле[5]
Значение полинома можно вычислять используя рекуррентную формулу для конкретного значения x. Производную также можно вычислять для конкретного значения x, используя формулу для производной.
Формулы с разложениями[править]
- Многочлены Лежандра также определяются следующими разложениями:
для ± :
и для ± :
Следовательно,
Присоединённые многочлены Лежандра[править]
Присоединённые многочлены Лежандра определяются по формуле:
которую также можно представить в виде:
При функция совпадает с .
Нормировка по правилу Шмидта[править]
Нормированные по правилу Шмидта полиномы Лежандра выглядят следующим образом[6]:
Сдвинутые многочлены Лежандра[править]
Сдвинутые многочлены Лежандра определяются как , где сдвигающая функция (это аффинное преобразование) — выбрана так чтобы однозначно отображать интервал ортогональности многочленов на интервал в котором уже ортогональны сдвинутые многочлены :
Явное выражение для смещённых многочленов Лежандра задаётся как:
Аналогом формулы Родрига для смещенных многочленов Лежандра является:
Выражения для некоторых первых сдвинутых многочленов Лежандра:
Матрица функции многочлена Лежандра[править]
Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны , где .
Первые многочлены Лежандра равны:
Поскольку , то
- При уравнение принимает вид
где — символ Кронекера.
- Для , норма равна:
- Нормированная функция многочленов Лежандра связана с нормой следующим соотношением:
- — четная функция;
- — нечетная функция.
Ряды многочленов Лежандра[править]
Разложение липшицевой функции в ряд многочленов Лежандра[править]
Липшицевая функция является функцией со свойством:
- , где .
Эта функция разлагается в ряд многочленов Лежандра.
Пусть — пространство непрерывных отображений на отрезке , и .
Пусть
тогда удовлетворяет следующему условию:
Пусть и удовлетворяет следующим условиям:
- , где
Липшецевую функцию можно записать следующим образом:
Разложение голоморфной функции[править]
Всякая функция f, голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:
Теорема сложения[править]
Для величин, удовлетворяющих условиям , , , — действительное число, можно записать теорему сложения для полиномов Лежандра первого рода:[7]
или, в альтернативной форме через гамма-функцию:
Для полиномов Лежандра второго рода теорема сложения выглядит как[8]
при условиях , , ,
Функции Лежандра[править]
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра ) естественно возникают в теории потенциала.
Шаровые функции — это функции (в сферических координатах ) вида (с точностью до константы)
- и
где — присоединённые многочлены Лежандра;
а точнее вида , где — сферические функции.
Шаровые функции удовлетворяют уравнению Лапласа всюду в .
- ↑ Градштейн, Рыжик, 1963, с. 1039
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 126—127
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 140
- ↑ Цимринг, 1988, с. 196
- ↑ 5,05,15,2 Цимринг, 1988, с. 197
- ↑ John W. Eaton, David Bateman, Søren Hauberg, Rik Wehbring. GNU Octave. — 2011. — С. 455-456.
- ↑ Градштейн, Рыжик, 1963, с. 1027
- ↑ Градштейн, Рыжик, 1963, с. 1028
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
- Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
- Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
- Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
- Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
- Цимринг Ш.Е. Специальные функции и определенные интегралы. Алгоритмы. Программы для микрокалькуляторов: Справочник. — М.: Радио и связь, 1988.
wp.wiki-wiki.ru
Реферат Полином Лежандра
скачатьРеферат на тему:
План:
- Введение
- 1 Определение
- 1.1 Формула Родрига
- 1.2 Формулы с Σ
- 1.3 Рекуррентная формула
- 1.4 Формулы с разложениями
- 1.5 Присоединённые многочлены Лежандра
- 2 Матрица функции многочлена Лежандра
- 3 Примеры
- 4 Свойства
- 5 Ряды многочленов Лежандра
- 5.1 Разложение липшицевой функции в ряд многочленов Лежандра
- 5.2 Разложение голоморфной функции
- 6 Функции Лежандра Литература
Введение
Многочлены Лежандра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
1. Определение
1.1. Формула Родрига
- Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде:
1.2. Формулы с Σ
- Многочлены Лежандра также определяются по следующим формулам:
- , если ;
- , если .
1.3. Рекуррентная формула
- Они также могут быть вычислены по рекуррентной формуле:
1.4. Формулы с разложениями
- Многочлены Лежандра также определяются следующими разложениями:
для ± :
и для ± :
Следовательно,
1.5. Присоединённые многочлены Лежандра
- Присоединённые многочлены Лежандра определяются по формуле:
которую также можно представить в виде:
При m = 0 функция совпадает с Pn.
2. Матрица функции многочлена Лежандра
Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны k(k + 1), где .
3. Примеры

Первые 6 многочленов Лежандра.
Первые многочлены Лежандра равны:
Поскольку Pn(1) = 1,
4. Свойства
- Присоединённые многочлены Лежандра являются решениями дифференциального уравнения
- Что также можно записать как:
- Производящая функция для многочленов Лежандра равна:
- Условие ортогональности этих полиномов на отрезке :
где δkl — символ Кронекера.
- Для , норма Pn равна:
- Нормированная функция многочленов Лежандра связана с нормой Pn следующим соотношением:
- При каждом m > 0 система присоединённых функций Лежандра полна в .
- В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
- — четная функция;
- — нечетная функция.
5. Ряды многочленов Лежандра
5.1. Разложение липшицевой функции в ряд многочленов Лежандра
Липшицевая функция f является функцией со свойством:
- , где L > 0.
Эта функция разлагается в ряд многочленов Лежандра.
Пусть — пространство непрерывных отображений на отрезке , и .
Пусть
тогда удовлетворяет следующему условию:
Пусть и удовлетворяет следующим условиям:
- , где
Липшецевую функцию f можно записать следующим образом:
5.2. Разложение голоморфной функции
Всякая функция f, голоморфная внутри эллипса с фокусами -1 и +1, может быть представлена в виде ряда:
6. Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра ) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах ) вида
- и
где — присоединённые многочлены Лежандра.
Сферические функции удовлетворяют уравнению Лапласа всюду в и служат ортогональным базисом для функций.
Литература
- Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
- Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
- Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
wreferat.baza-referat.ru


