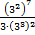Свойства степени с натуральным показателем
Свойства степени с натуральным показателем 7 класс
Свойство 1, формулаЕсли степени умножать ( при одинаковый основания), то показатели
степени сложить, основание остается неизменным.
am • an = am + n
Пример 33 • 3 4 = 37 = 2 187;42 • 43 = 45 = 1 024;
y3 • y5 = y8.
Свойство 2, формула Пример
(- 2)10 : (- 2)7 = (- 2)3 = 8;
Пример
(- 2)10 : (- 2)7 = (- 2)3 = 8;(0,1)101 : (0,1)
57 : 59 = 152 = 1 25.
Свойство 3, формулаЕсли основание не равно нулю, то любое основание в степени нуль,
равно единице.
a0 = 1
Пример 30 = 0;(? 5)0 = 1;
(- 2,5)0 = 1.
Свойство 4, формулаЕсли степень возвести в степень, то показатели — перемножить.
(am)n = amn
Пример (32)3 = 36 = 729.
Свойство 5, формулаЕсли произведение требуется возвести в степень, то каждый
множитель возводят в степень, и полученные результаты перемножают.
(ab)n = anbn
ПримерПример (0,9 • 2)2 = 0,92 • 22 = 0,81 • 4 = 1,62;
(3z)3 = 33z3=27z3.
Свойство 6, формулаЕсли требуется возвести в степень дробь, то возводят в степень
числитель и знаменатель.

При возведении отрицательного числа в степень, все зависит от
четности степени. Если степень четная, то и число получится четное,
если степень нечетная, то число останется со знаком «минус».

(- x)2 = x2;
(- z)3 = -z3;
(- 2ab)2 = (2ab)2 = 22a2b2 = 4a2b2.
Конспект «Алгебра 7 класс. Все формулы и определения»
Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.
«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: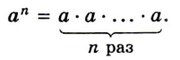 Степенью числа а с показателем 1 называют само число а: а1 = а.
Степенью числа а с показателем 1 называют само число а: а1 = а.
Степень числа а ≠ 0 с показателем 0 равна 1: а0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
аm • аn = аm+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
аm : аn = аm-n, где а ≠ 0, m ≥ n
(аm)n = аmn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab)n = аnbn
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
☑ 3. Одночленами
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а2b4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х5 – 4х2 + 1, 7a3b – ab2 + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х3у + 3х2у5 + ху равна степени одночлена 3х2у5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с2) + (ab – с2) = 3ab + 5с2 + ab – с2 = 4аb + 4с2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x2 – у) – (2x2 – 8у) = 6х2 – у – 2х2 + 8у = 4х2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а2 (3аb – b3 + 1) = 3а3b – а2b3 + а2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x2 – Зx + 10x – 2 = 15x2 + 7x – 2
☑ 6. Формулы сокращённого умножения
(а + b)2 = а2 + 2аb + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b)2 = а2 – 2аb + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b)3 = а3 + 3а2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b)3 = а3 – 3а2b + Заb2 – b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а2 – b2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а3 + b3 = (а + b)(a2 – аb + b2)
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а3 – b3 = (а – b)(a2 + ab + b2)
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х3 – х2у можно разложить на множители, вынеся за скобки х2 : 5х3 – х2у = х2 (5х – у). Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а4 – 25x2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а4 – 25x2 = (а2)2 – (5x)2 = (а2 – 5x)(а2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Уравнения
☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.
Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.
Например, уравнение 7х = 2 имеет корень 2/7.
Если а = 0 и b ≠ 0, то уравнение ах = b
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Функции
☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.
☑ 18. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
| 1. |
Умножение степеней
Сложность: лёгкое |
1 |
| 2. |
Степень в степени
Сложность: лёгкое |
1 |
| 3. |
Возведение степени в степень (буквы)
Сложность: лёгкое |
2 |
| 4. |
Степень в степени (основание)
Сложность: лёгкое |
2 |
| 5. |
Степень в степени (показатель степени)
Сложность: лёгкое |
2 |
| 6. |
Произведение трёх степеней
Сложность: лёгкое |
2 |
| 7. |
Произведение степеней (основание — бином)
Сложность: лёгкое |
1 |
| 8. |
Частное трёх степеней
Сложность: лёгкое |
2 |
| 9. |
Произведение степеней с одинаковыми основаниями (буквы)
Сложность: лёгкое |
3 |
| 10. |
Произведение двух степеней (числа)
Сложность: лёгкое |
2 |
| 11. |
Частное двух степеней (отрицательное основание)
Сложность: лёгкое |
2 |
| 12. |
Возведение степени в степень (числа)
Сложность: лёгкое |
2 |
| 13. |
Частное двух степеней (дробь)
Сложность: лёгкое |
3 |
| 14. |
Частное двух степеней (отрицательные смешанные числа)
Сложность: лёгкое |
1 |
| 15. |
Произведение степеней с одним основанием (числа)
Сложность: среднее |
3 |
| 16. |
Произведение отрицательных и противоположных степеней
Сложность: среднее |
5 |
| 17. |
Уравнение (частное степеней, целые числа)
Сложность: среднее |
3 |
| 18. |
Дробь (буквы)
Сложность: среднее |
2 |
| 19. |
Произведение степени и степени в степени
Сложность: среднее |
2 |
| 20. |
Деление и умножение степеней
Сложность: среднее |
3 |
| 21. |
Произведение двух дробей
Сложность: среднее |
2 |
| 22. |
Произведение степеней в степени
Сложность: среднее |
3 |
| 23. |
Частное степени в степени и степени
Сложность: среднее |
2 |
| 24. |
Умножение и деление степеней
Сложность: среднее |
1 |
| 25. |
Вычисление выражения со степенями
Сложность: среднее |
1 |
Свойства степеней | Алгебра
Основные свойства степеней задаются формулами:
(При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают).
(При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя).
(При возведении степени в степень основание оставляют прежним, а показатели перемножают).
(При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают).
(При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят).
Кроме того,
(где a≠0)
Если n — натуральное число, то
в частности,
в частности,
Для a>0
В частности,
В школьном курсе алгебры свойства степеней изучаются на протяжении нескольких лет: сначала для степени с натуральным показателем, затем — для степени с целым показателем, далее — для степени с рациональным и иррациональным показателем.
Свойства степеней с натуральным и целым показателем верны и для степеней с рациональными и иррациональными показателем, но накладывается дополнительное условие: основания степеней в этом случае должны быть положительными.
По определению, для любого α
Степень с натуральным показателем и её свойства. Видеоурок. Алгебра 7 Класс
Вспомним основные определения:
 – степень с натуральным показателем, здесь а – основание степени, n – показатель степени.
– степень с натуральным показателем, здесь а – основание степени, n – показатель степени.
Кроме того, напомним, что:
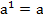 и
и 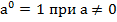 ;
;
Символ 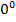 , как и символ
, как и символ 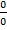 не имеет смысла.
не имеет смысла.
Все одночлены, многочлены и основные операции с ними основаны на степенях и действиях со степенями, которые мы сейчас вспомним:
Основные теоремы о действиях со степенями:
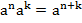 ;
;
Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым.
 ;
;
Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить тем же самым;
Пример 1: 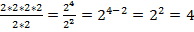
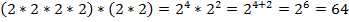
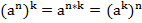 ;
;
Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.
Мы вспомнили основные правила работы со степенями с одинаковым основанием. В качестве примеров выведем еще несколько правил:
Пример 2: 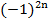 – возвести минус единицу в четную степень;
– возвести минус единицу в четную степень; 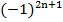 – возвести минус единицу в нечетную степень;
– возвести минус единицу в нечетную степень;
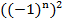 – при возведении в квадрат любое число станет положительным, единица в любой степени равна единице, таким образом, независимо от значения
– при возведении в квадрат любое число станет положительным, единица в любой степени равна единице, таким образом, независимо от значения  выражение
выражение 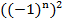 равно единице.
равно единице.
Конспект «Степени. Свойства степеней» — УчительPRO
Степени. Свойства степеней.
Ключевые слова конспекта: степень с натуральным показателем, основание степени, показатель степени, возведение в степень, дисперсия, умножение и деление степеней, свойства степеней.
Произведение 7 • 7 • 7 • 7 • 7 записывают короче: 75. Выражение вида 75 называют пятой степенью числа 7 (читают: «семь в пятой степени»). В записи 75 число 7, которое означает повторяющийся множитель, называют основанием степени, а число 5, показывающее, сколько раз этот множитель повторяется, называют показателем степени.
Умножим 75 на 73:
75 • 73 = (7 • 7 • 7 • 7 • 7) • (7 • 7 • 7) = 7 • 7 • 7 • 7 • 7 • 7 • 7 • 7 = 78.
Показатель степени увеличился на 3. Естественно считать, что 7 = 71. Вообще считают, что первой степенью числа является само число. Например, 181 = 18, 1041 = 104.
Степень с натуральным показателем
✅ Определение. Степенью числа а с натуральным показателем n, большим 1, называют выражение аn, равное произведению n множителей, каждый из которых равен а.
Степенью числа а с показателем 1 называют выражение а1, равное а.
По определению

Запись аn читается так: «а в степени n» или «n-я (энная) степень числа а». Для второй и третьей степеней числа используют специальные названия: вторую степень числа называют квадратом, а третью степень — кубом.
Возведение в степень
Нахождение n-й степени числа а называют возведением в n-ю степень.
Пример 1. Возведём число -3 в четвёртую и пятую степени:
(-3)4 = (-3) • (-3) • (-3) • (-3) = 81;
(-3)5 = (-3) • (-3) • (-3) • (-3) • (-3) = -243.
Из свойств умножения следует, что:
- при возведении нуля в любую степень получается нуль;
- при возведении положительного числа в любую степень получается положительное число;
- при возведении отрицательного числа в степень с чётным показателем получается положительное число, а при возведении отрицательного числа в степень с нечётным показателем — отрицательное число.
Пример 2. Возведём число 6,1 в седьмую степень, воспользовавшись калькулятором. Для этого надо выполнить умножение:
6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1.
Калькулятор позволяет выполнять возведение в степень проще, не повторяя основание степени и знак умножения. Для того чтобы возвести число 6,1 в седьмую степень, достаточно ввести число 6,1, нажать клавишу УМНОЖИТЬ и шесть раз нажать клавишу РАВНО . Получим, что 6,17 = 314274,28.
При вычислении значений числовых выражений, не содержащих скобки, принят следующий порядок действий: сначала выполняют возведение в степень, затем умножение и деление, далее сложение и вычитание.
Пример 3. Найдём значение выражения -62 + 64 : (-2)5. Последовательно находим:
1) 62 = 36;
2) (–2)5 = –32;
3) 64 : (–32) = –2;
4) –36 + (–2) = –38.
Пример 4. Найдём множество значений выражения 5 • (–1)n + 1 + 2, где n ∈ N.
Если n — нечётное число, то (-1)n + 1 = 1; тогда 5 • (-1)n + 1 + 2 = 5 • 1 + 2 = 7.
Если n — чётное число, то (-1)n + 1 = -1; тогда 5 • (-1)n + 1 + 2 = 5 • (-1) + 2 = -5 + 2 = -3.
Множество значений данного выражения: {-3; 7}.
В рассмотренном примере было указано, что n ∈ N. Условимся в дальнейшем такое указание опускать и считать, что если показатель степени содержит переменную, то значениями этой переменной являются натуральные числа.
Дисперсия
Степень с натуральным показателем широко используется в естествознании для вычисления различных характеристик. Например, в статистике, для того чтобы узнать, как числа некоторой выборки расположены по отношению к среднему арифметическому этой выборки, используют отклонения, их квадраты и среднее арифметическое квадратов отклонений — дисперсию.
Пример 5. Дана выборка: 4, 6, 7, 8, 10. Среднее арифметическое этой выборки равно 7. Тогда отклонения вариант данной выборки от среднего арифметического равны: 4 – 7 = –3, 6 – 7 = –1, 7 – 7 = 0,8 – 7 = 1, 10 – 7 = 3, т. е. мы получили ещё один набор чисел — отклонения каждой варианты выборки от среднего арифметического. По новой выборке (–3; –1; 0; 1; 3) можно судить о том, насколько близки к среднему арифметическому числа исходного набора. Но поскольку сумма отклонений равна нулю, то и среднее арифметическое этой новой выборки также равно нулю. Поэтому для дальнейших исследований исходного набора находят квадраты отклонений и их среднее арифметическое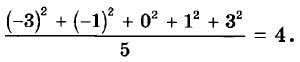
Полученное число и есть дисперсия исходной выборки.
Умножение степеней
Представим произведение степеней а5 и а2 в виде степени:
а5 • а2 = (а • а • а • а • а) • (а • а) = а • а • а • а • а • а • а = а7.
Мы получили степень с тем, же основанием и показателем, равным сумме показателей множителей. Подмеченное свойство выполняется для произведения любых двух степеней с одинаковыми основаниями.
Если а — произвольное число, m и n — любые натуральные числа, то аm • аn = аm+ n
Докажем это. Из определения степени и свойств умножения следует, что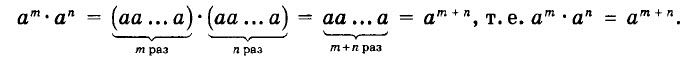
Доказанное свойство называется основным свойством степени. Оно распространяется на произведение трёх и более степеней. Это нетрудно показать с помощью таких же рассуждений.
Из основного свойства степени следует правило:
- чтобы перемножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели степеней сложить.
Деление степеней
Представим теперь в виде степени частное степеней а8 и а3, где а ≠ 0. Так как а3 • а5 = а8, то по определению частного а8 : а3 = а5.
Мы получили степень с тем же основанием и показателем, равным разности показателей делимого и делителя. Такое свойство выполняется для частного любых степеней с одинаковыми основаниями, не равными нулю, у которых показатель делимого больше показателя делителя.
Если а — произвольное число, не равное нулю, m и n — любые натуральные числа, причём m > n, то аm : аn = аm — n, где а ≠ 0, m ≥ n
Докажем это. Умножим аm — n на аn, используя основное свойство степени:
am – n • an = a(m – n) + n = am – n + n = am
Из доказанного свойства следует правило:
- чтобы выполнить деление степеней с одинаковыми основаниями, надо основание оставить тем же, а из показателя делимого вычесть показатель делителя.
Степень с нулевым показателем
Мы рассматривали степени с натуральными показателями. Введём теперь понятие степени с нулевым показателем.
✅ Определение. Степенью числа а, где а ≠ 0, с нулевым показателем называется выражение а0, равное 1.
Например, 50 = 1; (–6,3)0 = 1. Выражение 00 не имеет смысла.
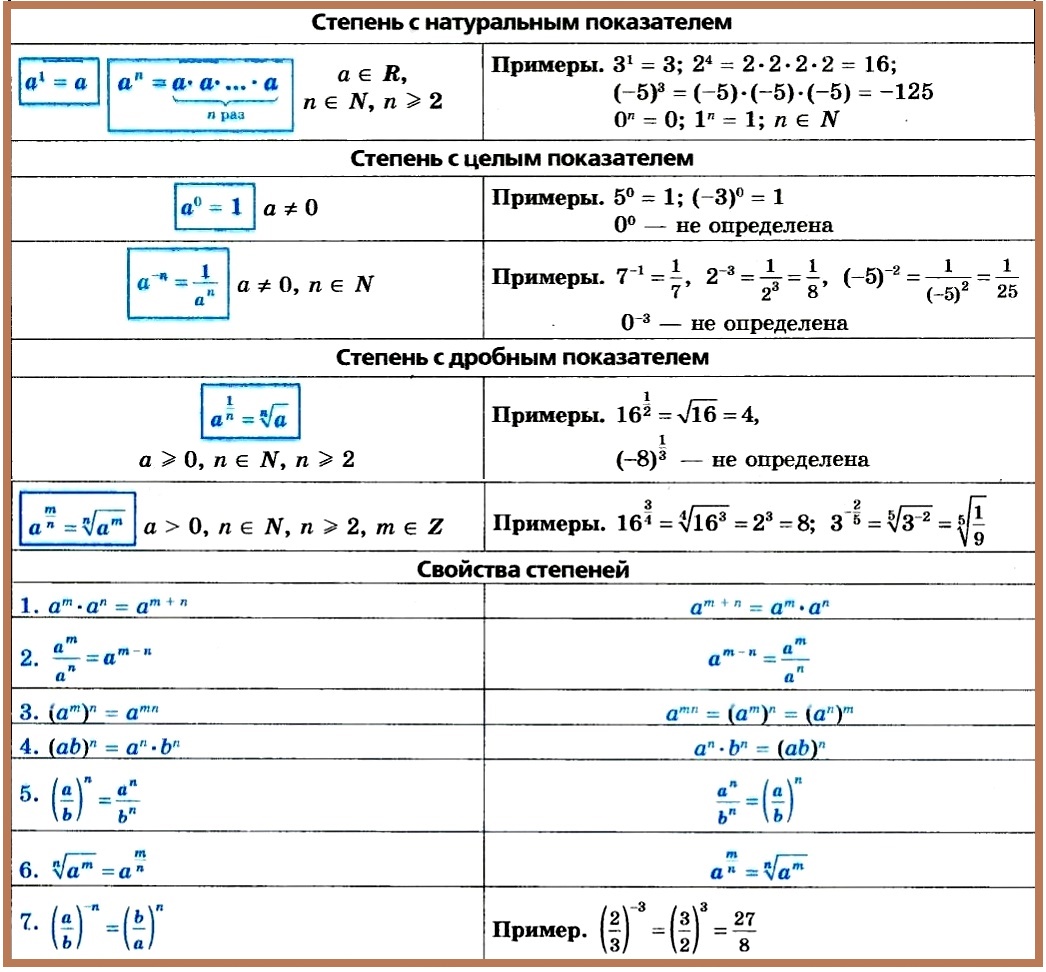
Это конспект по математике на тему «Степени. Свойства степеней». Выберите дальнейшие действия:
Возведение степени в степень (формула (an)k=ank)
На этом уроке мы изучим возведение степени в степень. Вначале вспомним определение степени и теоремы об умножении и делении степеней с одинаковым основанием. Далее будет сформулирована теорема о возведении степени в степень. Затем мы приведем примеры ее использования на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач и будем решать типичные примеры с помощью всех теорем.
Напоминание:
Основные определения:
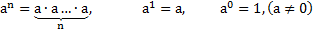
Здесь a – основание степени,
n – показатель степени,
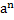 – n-ая степень числа.
– n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
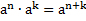
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:

При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
На этом уроке будет рассмотрена следующая теорема.
Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:
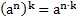
Вывод: частные случаи подтвердили правильность формулы 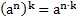 . Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
По определению степени:
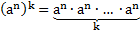
Применим теорему 1:
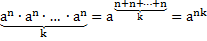
Итак, мы доказали: 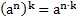 , где а – любое число, n и k – любые натуральные числа.
, где а – любое число, n и k – любые натуральные числа.
Другими словами, чтобы возвести степень в степень показатели нужно перемножить, а основание оставить неизменным.
Пример 1: Упростить.
Для решения следующих примеров воспользуемся свойством 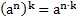 .
.
а) 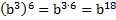
б)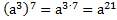
в) 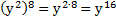
Комментарий к примеру 1.
Мы написали, что 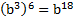 , но в то же время
, но в то же время  , так как
, так как  .
.
Аналогично, 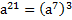
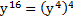 .
.
В качестве основания может быть любое допустимое алгебраическое выражение:
Пример 2:Упростить.
а) 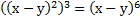
б) 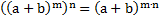
Пример 3: Вычислить.
а) 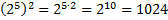
б) 
в) 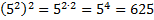
г)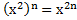 . Комментарий:
. Комментарий: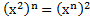
д)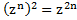 . Комментарий:
. Комментарий: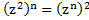
е)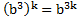 . Комментарий:
. Комментарий: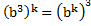
Пример 4: Упростить.
Для решения следующих примеров будем пользоваться теоремами 1, 2, 3.
а) 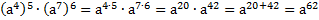
б) 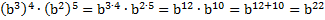
в) 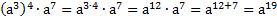
г)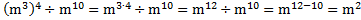
д)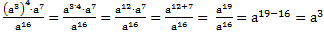 или быстрее
или быстрее 
е)  =
= 
Пример 5: Вычислить:
а)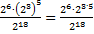 =
=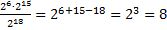
Список литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Mirurokov.ru (Источник).
- Школьный помощник (Источник).
- Интернет-портал Testent.ru (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
Домашнее задание
- Упростить:
а) б)
б)  в)
в) 
- Вычислить:
а) б)
б)  ; в)
; в) 
- Упростить:
а) б)
б) в)
в)  г)
г) 
- Вычислить:
а) б)
б)



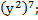 б)
б) 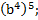 в)
в) 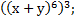
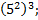 б)
б)  ; в)
; в) 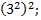
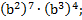 б)
б)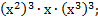 в)
в) 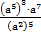 г)
г) 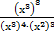
 б)
б)