Острый угол равен – Острый угол | Треугольники

Какой угол называется острым? прямым? тупым?

Острый угол, угол < 90 градусов. Прямой угол = 90 градусов. Тупой угол > 90 градусов.

Остр. — <90° Прямой — 90° Тупой — >90°

Угол, который меньше 90 градусов, называется-острым Угол, равный 90 градусам, называется-прямым Угол, который больше 90 градусов, называется-тупым

Прямым называется угол, который равен 90 градусам, острый угол меньше прямого, а тупой-больше прямого. И на справку: есть ещё развёрнутый угол, который равен 180 градусам.

Возьми свой транспортир, острым называется тот, у которого меньше 90 градусов. Идёт от 0 до 90 градусов. У прямого только 90 градусов, обычный угол, который чаще всего везде встречается. Тупой: более широкий, больше 90 градусов, и до 180.

touch.otvet.mail.ru

Острый угол — это… Что такое Острый угол?

«∠», обозначение угла в математике

Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).

Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.

Иногда, для краткости, углом называют угловую меру.

Угловая мера

Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.

1 оборот = 2π радианам = 360° = 400 градам.

В системе СИ принято использовать радианы.

В морской терминологии углы обозначаются румбами.

Углы на тригонометрической окружности

В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.

В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.

Типы углов

Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.

Центральные и вписанные углы окружности.

В зависимости от величины углы разделяются на:

Невыпуклый угол

Прямой угол

Вариации и обобщения

Величиной ориентированного угла между прямыми AB и CD (обозначение: ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме или, что по нашему соглашению то же самое, ). Ориентированные углы обладает следующими свойствами: а) ; б) ; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда .

Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).

Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.

Wikimedia Foundation. 2010.

dic.academic.ru

Углы в геометрии. Сторона угла. Прямой угол, острый угол, тупой угол, развернутый угол. Измерение углов

Угол

Что такое угол в геометрии?

Угол в геометрии: если провести из данной точки два различных луча, то получим геометрическую фигуру – угол.

Точка, из которой исходят эти лучи, называется вершиной угла, а сами лучи называют сторонами угла.

На картинке изображен угол AOB, O – вершина угла AOB, OA и OB – стороны угла AOB:

Измерения углов

Измеряются углы в градусах.

Один градус – это угол, величиной в 1/180 часть развернутого угла. 1/60 часть градуса – это минута, а 1/60 часть минуты – это секунда. Пример:

45⁰20’12»

это угол в 45 градусов, 20 минут, 12 секунд.

Развернутый угол

Развернутый угол – это угол, обе стороны которого лежат на одной прямой. Величина развернутого угла 180⁰:

Прямой угол

Прямой угол – это угол величиной в 90⁰:

Острый угол

Острый угол – это угол величиной менее 90

0:

Тупой угол

Тупой угол – это угол величиной более 90⁰, но менее 180⁰:

Смежные углы

Смежные углы – это углы, у которых одна сторона общая. а две другие лежат на одной прямой:

На картинке углы AOB и BOC являются смежными.

Сумма смежных углов равна 180⁰, это свойство смежных углов.

Вертикальные углы

Вертикальные углы – это углы, у которых стороны являются продолжениями друг друга:

На картинке имеются две пары вертикальных углов: первая пара – углы AOB и DOC являются вертикальными, вторая пара – углы AOD и BOC являются вертикальными.

Вертикальные углы равны между собой.

В нашем примере вертикальные углы AOB и DOC равны между собой, и вертикальные углы AOD и BOC равны между собой.

www.sbp-program.ru

Внеклассный урок — Углы

Углы

 

Основные понятия.

Угол – это фигура, образованная двумя лучами, выходящими из одной точки.

Вершина угла – это точка, из которой выходят два луча, образующих этот угол.

Биссектриса – это луч, который выходит из вершины угла и делит угол пополам.

Развернутый угол – это угол, стороны которого лежат на одной плоскости; равен 180˚ и является прямой.

Прямой угол – это угол, равный половине развернутого угла; равен 90˚.

Острый угол – это угол, который меньше прямого.

Тупой угол – это угол, который больше прямого, но меньше развернутого.

Угол разбивает плоскость на две части. Каждая из частей называется плоским углом.

Плоские углы с общими сторонами называются дополнительными.

Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.

Если плоский угол содержит полуплоскость, то его градусная мера равна 360^º – α, где α – градусная мера дополнительного плоского угла.

 

Равные углы.

Это углы, которые совпадают при наложении.

 

Смежные углы.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

 На рисунке углы (ad) и (cd) смежные. У них сторона d общая, а стороны a и c – дополнительные полупрямые. 

Теорема:
Сумма смежных углов равна 180^º.

Из теоремы следует:
— если два угла равны, то смежные с ними углы равны.
— если угол не развернутый, то его градусная мера меньше 180^º.
— угол, смежный с прямым углом, есть прямой угол.

 

Вертикальные углы.

Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Они созданы пересечением двух прямых и не являются прилегающими, имеют общую вершину и одинаковую градусную меру.

 На рисунке углы (A₁ B₁) и (A₂ B₂) вертикальные. Стороны A₂ и B₂ второго угла являются дополнительными полупрямыми сторон A₁ и B₁ первого угла.

 

  Центральный угол.

Центральным углом в окружности называется плоский угол с вершиной в ее центре (рис.1).

Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (на рис.1 дуга AB является дугой окружности).

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

 

Угол, вписанный в окружность.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис.2).

Свойства:

1) Вписанный угол равен половине соответствующего центрального угла (на рис.3 вписанный угол ABC равен половине соответствующего ему центрального угла AOC). 2) Вписанный угол, опирающийся на диаметр, равен 90° (рис.4). 3) Вписанный угол, опирающийся на хорду, равную радиусу окружности, равен 30°.

 

 Углы при пересечении двух прямых третьей.

При пересечении прямых a и b секущей c образуется восемь углов, которые на рисунке обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7. 

  
 
 

 

 

 

raal100.narod.ru

Острый угол прямоугольного треугольника равен

Для вас несколько заданий — в условии дан прямоугольный треугольник. В условии говорится о вычислении углов между высотой и биссектрисой, медианой и биссектрисой, высотой и медианой проведёнными из прямого угла.

Это группа заданий входит в состав ЕГЭ по математике. Задачи несложные, требуется знание теоремы о сумме углов треугольника, свойств равнобедренного треугольника и немного логики. Да! Есть один нюанс — задачи, в  которых говорится о медиане проведённой к гипотенузе необходимо знать одно свойство, теорию можно посмотреть здесь. Приступим!

Один острый угол прямоугольного треугольника в 4 раза больше другого.  Найдите больший острый угол. Ответ дайте в градусах.

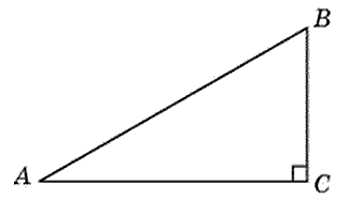
Обозначим меньший острый угол прямоугольного треугольника через x. Тогда больший острый угол данного  треугольника будет равен 4х.

По свойству прямоугольного треугольника сумма его острых углов равна 90^о. Отсюда получаем уравнение  х + 4х = 90^о.

Вычисляем, получим 5х = 90^о,  х = 18^о.

Следовательно больший угол будет равен 18^о ∙ 4 = 72^о

Ответ: 72

Острый угол прямоугольного треугольника равен 32^о. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

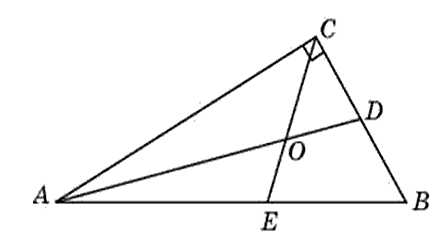
Нам необходимо найти угол COD. По условию известно, что CE и AD  — это  биссектрисы (делят углы пополам). Это означает, что угол CAD равен 32^о, а угол ACO равен 45^о. По теореме о сумме углов треугольника мы можем найти угол AOC, и далее угол COD. Итак, известно, что сумма углов треугольника равна 180^о, следовательно

Углы AOC и COD  смежные, то есть их сумма равна 180^о. Таким образом, искомый угол (острый угол между данными биссектрисами) равен 61 градусу.

Ответ: 61

*Если в подобных задачах вы сразу не видите ход решения, то ищите те элементы, которые можно найти исходя из условия в первую очередь. А далее уже используйте найденные значения.

Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

В условии нам не даны ни какие величины, кроме того, что угол С прямой. Это говорит  о том, что их необходимо ввести, то есть в данном случае мы можем обозначить угол через переменную,  а далее использовать свойства прямоугольного треугольника и теорему о сумме углов.

Обозначим угол CAD как х. Тогда угол CBA будет равен 90^о – х.

Рассмотрим треугольник AOB:

Можем найти угол AOB:

Значит острый угол между биссектрисами будет равен 45^о, так является смежным углу 135^о.

Как видите, не всегда нужны численные величины в условии. Достаточно знать свойства, включить логику и задача будет решена.

Ответ: 45

В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21^о. Найдите меньший угол данного треугольника. Ответ дайте в градусах. 

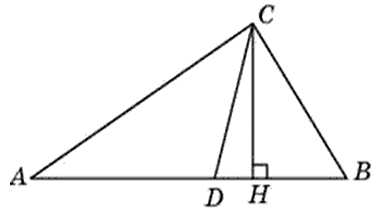
Сразу отметим, что в треугольнике CDH нам известны два угла. Используя теорему о сумме углов треугольника мы можем найти угол CDH. То есть:

Теперь мы можем найти угол В в треугольнике CDВ. Так как CD биссектриса, то угол BCD равен 45^о, угол CDB мы нашли.

Значит угол В равен 180^о–45^о–69^о=66^о. По свойству прямоугольного треугольника: сумма острых углов в нём равна 90 градусов.

Следовательно  другой острый угол будет равен 24^о.

Ответ: 24

Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14^о. Найдите меньший угол этого треугольника. Ответ дайте в градусах. 

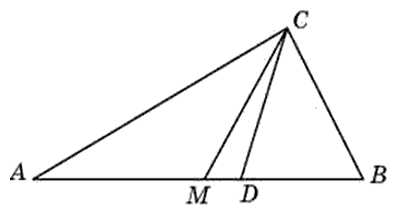
Нам дан угол MCD равный 14^о. Так же нам известен угол DCB, он равен 45^о, так как CD биссектриса. Можем найти угол MCB: 14^о + 45^о = 59^о.

Как уже сказано, медиана в прямоугольном треугольнике проведённая из прямого угла к гипотенузе равна её половине. То есть, она разбивает прямоугольный треугольник на два равнобедренных треугольника, в данном случае AMC и BMC. Известно, что в равнобедренном треугольнике углы при основании равны, то есть угол MBC равен углу BCM. Таким образом,

То есть, меньший угол равен 31^о.

Ответ: 31

Один острый угол прямоугольного треугольника на 32^о  больше другого. Найдите больший острый угол. Ответ дайте в градусах.

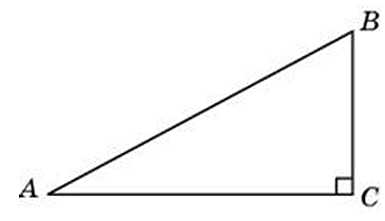
Посмотреть решение

В треугольнике АВС угол С равен 90^о, СН  — высота, угол А равен 34^о. Найдите угол ВСН. Ответ дайте в градусах.

Посмотреть решение

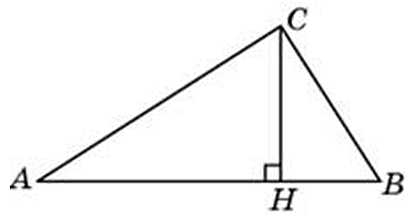
В треугольнике ABC CD  — медиана, угол ACB равен 90^о, угол В равен 58^о. Найдите угол ACD. Ответ дайте в градусах.

Посмотреть решение

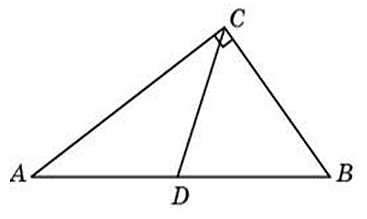
Острые углы прямоугольного треугольника равны 29^о  и 61^о. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

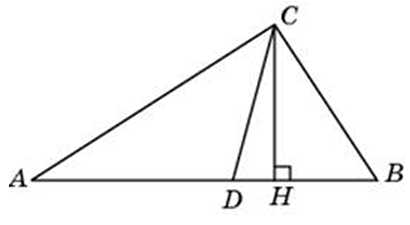
Острые углы прямоугольного треугольника равны 24^о и 66^о. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40^о. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Посмотреть решение

Острые углы прямоугольного треугольника равны 24^о и 66^о. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

Какие общие рекомендации можно дать?

1. Используйте теорему о сумме углов треугольника. Это одна из основных теорем, связанных с треугольниками, её нужно всегда помнить.

2. Нужно чётко помнить, что такое медиана, биссектриса, высота (не перепутать).

3. Запомните свойство медианы  в прямоугольном треугольнике.

4. В задачах, где в условии не даны численные величины углов, обозначайте их переменной(ыми) и далее используйте известные вам свойства.

5. Если не видите каким путём строить решение, и сразу не можете увидеть логическую цепочку рассуждений, то исходя из данных в условии ищите то, что возможно найти. Получив новые величины, также смотрите, что вы можете найти при их использовании.

На этом всё. Успеха Вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Что такое тупой угол?

Если градусная мера угла больше 90 и меньше 180 градусов, то такой угол называют тупым (рисунок 1).
Если обозначить угол , то для тупого угла запишем .

Рисунок 1
Тупой угол является большим от прямого и меньшим от развернутого.

Пример.
На рисунке 2 изображены углы. Назовите, какие из них острые и какие тупые.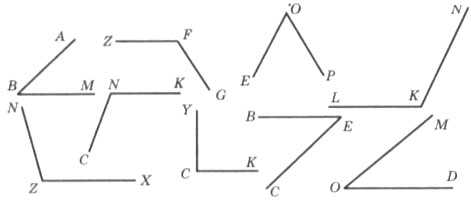

Рисунок 2
Решение.
Назовем тупые углы – ZFG, LKN, NZX, CNK.
Острые углы (градусная мера меньше 90 градусов) – ABM, EOP, BEC, MOD.
Угол YCK – прямой (градусная мера равна 90 градусов, такой угол не является ни острым, ни прямым).

Пример.
Острый угол параллелограмма  равен 53 градуса. Найти тупой угол данного параллелограмма.

Решение.
Так как сумма углов параллелограмма, которые прилегают к одной стороне, равна 180 градусов, то тупой угол, который необходимо найти, будет равен:

   

Ответ:

Пример.
Треугольник имеет два острых и один тупой угол. Острые углы равны 28 и 34 градуса. Найти тупой угол.
Решение. Обозначим искомый тупой угол – х. По теореме о сумме углов треугольника известно, что:

   

Найдем неизвестное:

   

Ответ. Тупой угол треугольника равен .

ru.solverbook.com

Один из острых углов прямоугольного треугольника равен 34градуса.Найти второй острый угол треугольника

Сумма углов треугольника всегда равна 180 градусам. Если треугольник прямоугольный, значит один из его углов равен 90 градусам. Второй угол — по условию задачи — 34 градуса. Соответственно, третий угол равен 180-90-34 =56 градусов

56 градусов, соответствено. Не то нажал сначала:)

Ну ты дашь…. На такой вопрос и отвечать стыдно

так как в треугольнике 180 градусов, а прямой это 90 гр, то получаем: 180-(90+34)=??

Сумма всех углов равна 180. Значит 56

геометрия 5-6 класс

Танюшка задала вопрос-шутку, а все начали считать!

touch.otvet.mail.ru

No related posts.