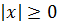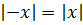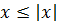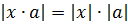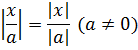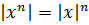Модуль числа примеры: 6.2.4. Модуль числа   математика-повторение – Модуль числа — знак, свойства, действия, как найти, примеры графиков

6.2.4. Модуль числа   математика-повторение

Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.

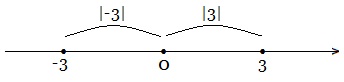
Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам. Противоположные числа имеют равные модули. Модуль нуля равен нулю: |0|=0.

По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а<0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.

Примеры.

1. Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|;

г) |65|-|-45|.

Решение. а) |5|-2=5-2=3;

б) |-12| : 6=12 : 6=2;

в) |-24|+|13|=24+13=37;

г) |65|-|-45|=65-45=20.

2. Решить уравнение: а) |m|+4=10; б) 6-|x|=2.

Решение.

а) |m|+4=10;

|m|=10-4; из суммы вычли известное слагаемое;

|m|=6. Так как |-6|=6  и  |6|=6, то m=-6  или m=6.

Ответ: -6; 6.

б) 6-|x|=2.

|x|=6-2;

|x|=4, отсюда х=-4 или х=4.

Ответ: -4; 4.

3. Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.

Решение. По определению модуля числа 5 искомые числа должны отстоять от начала отсчета как вправо, так и влево на расстояние, меньшее пяти единичных отрезков. В этом промежутке (показан штриховкой на рисунке) бесконечно много чисел, но нам нужно выбрать из них лишь все целые числа. Берем числа: -4, -3, -2, -1, 0, 1, 2, 3, 4.

Числа -5 и 5 не подходят по условию.

Ответ:  множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.

4. Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.

Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т.е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.

 

 

Модуль числа — знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам. Заработай деньги с помощью своих знаний на https://teachs.ru!

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

1. Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
2. Если абсолютные значения содержат выражения противоположных значений, они равны:
3. Значение числа не превышает величину его модуля:
4. Правило раскрытия при произведении:
5. Правило, применимое при делении:
6. При возведении в степень:
7. Сумма величин:
8. Двойной модуль:

Модуль комплексного числа

Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| < a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке  величина будет отрицательной, а на интервале  будет положительной.

Разделим интервал на 2 части:

1. для x + 2 ≥ 0

Общим ответом для этих двух неравенств является интервал [−1; + ∞).

2. для х + 2 < 0

Общим ответом для этих двух неравенств является интервал (−∞; –3].

Окончательное решение – объединение ответов отдельных частей:

x ∈ (–∞; –3] ∪ [–1; + ∞).

Ответ: x ∈ (–∞; –3] ∪ [–1; + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x₁ = 3; x₂ = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что  не лежит в промежутке .

Ответ: x = 0.

Модуль суммы

Модуль разности

Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Известно свойство:

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него;
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение;
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Модуль числа. | tutomath

Модуль числа вводится новое понятие в математике. Разберем подробно, что такое модуль числа и как с ним работать?

Рассмотрим пример:

Мы вышли из дома в магазин. Прошли 300 м, математически это выражение можно записать как +300, смысл числа 300 от знака “+” не поменяется. Расстояние или модуль числа в математике это одно и тоже можно записать так: |300|=300. Знак модуля числа обозначается двумя вертикальными линиями.

А потом в обратном направлении прошли 200м. Математически обратный путь мы можем записать как -200. Но мы не говорим так “мы прошли минус двести метров”, хотя мы вернулись, потому что расстояние как величина остается положительной. Для этого в математике ввели понятие модуля. Записать расстояние или модуль числа -200 можно так: |-200|=200.

Свойства модуля.

Определение:
Модуль числа или абсолютная величина числа – это расстояние от отправной точки до точки назначения.

Модуль целого числа не равного нулю, всегда положительное число.

Записывается модуль так:

1. Модуль положительного числа равно самому числу.
|a|=a

2. Модуль отрицательного числа равно противоположному числу.
|-a|=a

3. Модуль нуля, равен нулю.
|0|=0

4. Модули противоположных чисел равны.
|a|=|-a|=a

Вопросы по теме:
Что такое модуль числа?
Ответ: модуль — это расстояние от отправной точки до точки назначения.

Если перед целым числом поставить знак “+” , что произойдет?
Ответ: число не поменяет свой смысл, например, 4=+4.

Если перед целым числом поставить знак “-” , что произойдет?
Ответ: число изменится на противоположное число, например, 4 и -4.

У каких чисел одинаковый модуль?
Ответ: у положительных чисел и нуля модуль будет тот же. Например, 15=|15|.

У каких чисел модуль – противоположное число?
Ответ: у отрицательных чисел, модуль будет равен противоположному числу. Например, |-6|=6.

Пример №1:
Найдите модуль чисел: а) 0 б) 5 в) -7?

Решение:
а) |0|=0
б) |5|=5
в)|-7|=7

Пример №2:
Существуют ли два различных числа, модули которых равны?

Решение:
|10|=10
|-10|=10

Модули противоположных чисел равны.

Пример №3:
Какие два противоположных числа, имеют модуль 9?

Решение:
|9|=9
|-9|=9

Ответ: 9 и -9.

Пример №4:
Выполните действия: а) |+5|+|-3| б) |-3|+|-8| в)|+4|-|+1|

Решение:
а) |+5|+|-3|=5+3=8
б) |-3|+|-8|=3+8=11
в)|+4|-|+1|=4-1=3

Пример №5:
Найдите: а) модуль числа 2 б) модуль числа 6 в) модуль числа 8 г) модуль числа 1 д) модуль числа 0.
Решение:

а) модуль числа 2 обозначается как |2| или |+2| это одно и тоже.
|2|=2

б) модуль числа 6 обозначается как |6| или |+6| это одно и тоже.
|6|=6

в) модуль числа 8 обозначается как |8| или |+8| это одно и тоже.
|8|=8

г) модуль числа 1 обозначается как |1| или |+1| это одно и тоже.
|1|=1

д) модуль числа 0 обозначается как |0|, |+0| или |-0| это одно и тоже.
|0|=0

Модуль числа

Мóдуль числá a — это расстояние от начала координат до точки А(a).

Чтобы понять это определение, подставим вместо переменной a любое число, например 3, и снова прочитаем его:

Мóдуль числá 3 — это расстояние от начала координат до точки А(3).

То есть модуль это ни что иное как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)

Расстояние от начала координат до точки А(3) составляет 3 (три единицы или три шага).

Модуль числа обозначает двумя вертикальными линиями, например:

Модуль числа 3 обозначается так: |3|

Модуль числа 4 обозначается так: |4|

Модуль числа 5 обозначается так: |5|

Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:

|3| = 3

Читается как «Модуль числа три равен три»

Теперь попробуем найти модуль числа −3. Опять же возвращаемся к определению и подставляем в него число −3. Только вместо точки A используем новую точку B. Точку A мы уже использовали в первом примере.

Модулем числа −3 называют расстояние от начала координат до точки B(−3).

Расстояние от одного пункта до другого не может быть отрицательным. Модуль это тоже расстояние, поэтому тоже не может быть отрицательным.

Модуль числа −3 равен 3. Расстояние от начала координат до точки B(−3) равно трём единицам:

|−3| = 3

Читается как «Модуль числа минус три равен три»

---

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает  с началом координат. То есть расстояние от начала координат до точки O(0) равно нулю:

|0| = 0

«Модуль нуля равен нулю»

Сделаем выводы:

• Модуль числа не может быть отрицательным;
• Для положительного числа и нуля модуль равен самомý числу, а для отрицательного – противоположному числу;
• Противоположные числа имеют равные модули.

---

Противоположные числа

Числа, отличающиеся только знаками называют противоположными.

Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числá −2 знак минуса, а у числá 2 знак плюса, но мы его не видим, поскольку плюс как говорилось ранее, не записывают.

Еще примеры противоположных чисел:

−1 и 1

−3 и 3

−5 и 5

−9 и 9

Противоположные числа имеют равные модули. Например, найдём модули чисел −3 и 3

|−3| и |3|

3 = 3

На рисунке видно, что расстояние от начала координат до точек A(−3) и B(3) одинаково равно трём шагам.

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Модуль числа. Видеоурок. Математика 6 Класс

Положительные числа, натуральные, а затем и дробные мы ввели для указания количества: 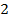 дерева,  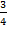литра молока (рис. 1).

Рис. 1. Пример использования положительных чисел

Затем мы ввели отрицательные числа: например, 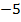. Теперь число, кроме количества, содержит еще и знак, который указывает, что нужно делать с этим количеством – добавить или отнять. То есть после того, как были введены отрицательные числа, мы можем сказать, что любое число состоит из количества (реально существующего) и знака (придуманного нами для упрощения записи арифметических действий).

Но иногда бывает важна только одна характеристика – количество, а знак нас не интересует.

Рассмотрим такой пример. Для таксиста важно, какой длины путь он преодолевает с пассажиром (рис. 2).

Рис. 2. Километраж

Ведь, если в конце поездки пассажира привозят обратно домой, это не означает, что он ничего таксисту не должен, так как он проехал какое-то расстояние с начала поездки (рис. 3).

Рис 3. Путь, проделанный такси

Пусть теперь такси может ездить только вдоль прямой (вправо или влево). У нас уже есть подходящая модель – координатная прямая (рис. 4).

Рис. 4. Аналогия с координатной прямой

Предположим, клиенты проехали 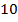 км влево, затем  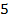км вправо, затем ещё  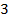км вправо, затем ещё  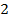км влево. В результате автомобиль отъехал на  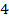км влево от исходной точки:  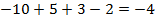(рис. 5).

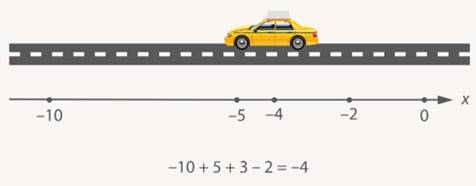
Рис. 5. Сколько проехала машина (считаем с помощью числовой прямой)

Но ведь путь, который проделало такси, значительно больше: 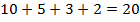 км.

Для подсчёта пути мы складывали только количества, без учёта знака.

Ту часть числа, которая указывает на количество, называют абсолютным значением (или модулем числа). То есть можно сказать и так: любое число состоит из знака и абсолютного значения (модуля). Если знак плюс, то для краткости его обычно не пишут.

Например, у числа 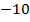 знак минус и модуль 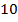, у числа 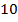, знак плюс и модуль  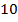(рис. 6).

Рис. 6. Из чего состоят противоположные числа

Пример: машина проехала 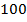 км по дороге. Используем для этой ситуации математическую модель – числовую прямую. Машина из точки  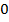могла двигаться вправо или влево. Можно так и говорить: перемещение на  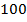км вправо, перемещение на  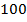км влево. Но у нас есть удобный инструмент, отрицательные числа. Поэтому короче мы можем говорить так: перемещение  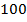или перемещение  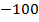(рис. 7).

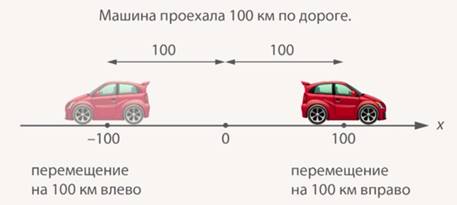
Рис. 7. Возможные движения машины

Перемещение было разное, но удалился автомобиль от начальной точки (от 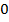) на одно и то же расстояние – на  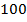км. Но  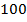– это и есть модуль (как для числа 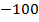, так и для ).

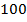То есть про модуль числа можно сказать и так: модуль – это расстояние от числа до нуля (на самом деле это определение более универсальное, но об этом вы узнаете в старших классах).

В физике два этих понятия так и называют:

• перемещение: для него важен результат – где были и где оказались в итоге;
• путь: здесь важно расстояние, которое мы прошли, и не важно, где мы оказались в итоге.

Так, если машина, двигалась из точки 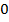 вправо  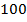км, а потом влево  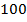км, то она вернется в начальную точку. Перемещение равно 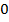, но путь равен  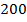км (рис. 8).

Рис. 8. Перемещение и путь

Перемещение от одной точки до другой изображают отрезком со стрелкой. Называют его вектором (рис. 1).

Рис. 9. Вектор

Здесь ситуация как с числами: есть количественная часть (длина) и есть направление (у числа их было всего два (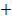 и 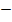), а здесь направлений может быть бесконечно много).

Сам вектор обозначают со стрелкой сверху. Длину вектора называют модулем (помните, как и у числа: модуль – это количественная часть) и обозначают с прямыми скобками или просто как отрезок (рис. 2).

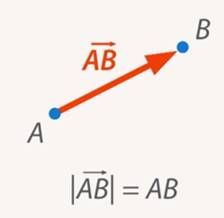
Рис. 10. Обозначение вектора и его длины

Если нам нужно попасть из одной точки в другую, мы не всегда можем пройти по прямой. Например, из точки 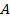 мы движемся в точку 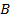, обходя газон, по которому ходить запрещено. То есть мы переместились два раза 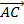и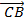. Итоговое перемещение  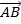(рис. 3).

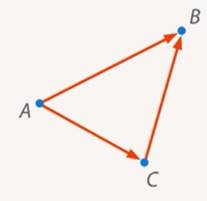
Рис. 11. Перемещение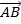

Перемещение 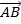 – это сумма двух перемещений 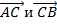: 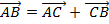. Для путей это не верно. Длина отрезка  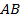меньше суммы длин отрезков  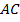и 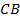: 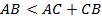. Путь по прямой короче, чем в обход.

Все это можно записать одним неравенством: 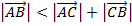. Оно означает вот что: сумма двух перемещений – это итоговое перемещение. Его длина меньше, чем сумма длин каждого перемещения по отдельности: .

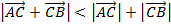Подумайте, может ли здесь быть равенство, если по-другому будут расположены векторы перемещения? А противоположный знак, то есть знак ?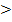

Рассмотрим такой пример. Человек гуляет с собакой, он движется из точки 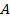 в точку  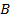по прямой, при этом собака движется еще из стороны в сторону, насколько позволяет поводок (рис. 4).

Рис. 12. Иллюстрация к примеру

Перемещение человека 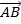 (рис. 5).

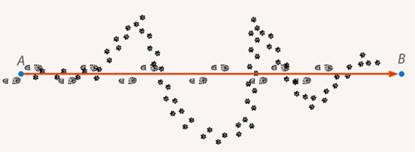
Рис. 13. Перемещение человека

Перемещение собаки складывается из кусочков и тоже в итоге равно &nbs

Как решать уравнения с модулем

Одна из самых сложных тем для учащихся  – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля. Итак,  модулем числа a называется само это число, если a неотрицательно и  -a, если  число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее  координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

                             {±c, если с > 0

 Если |x| = c, то x = {0, если с = 0

                             {нет корней, если с < 0

Примеры:

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

Примеры:

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

x = 2             x = -6

2) |x² – 5| = 11, т.к. 11 > 0, то

x² – 5 = 11 или x² – 5 = -11

x² = 16            x² = -6

x = ± 4             нет корней

3) |x² – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x).

Примеры:

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

              5x ≥ 10  

               x ≥ 2.  

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3x = 9                     7x = 11

x = 3                       x = 11/7

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3  

2) |x – 1| = 1 – x².

1. О.Д.З. 1 – x² ≥ 0. Решим методом интервалов данное неравенство:

             (1 – x)(1 + x) ≥ 0

             -1 ≤ x ≤ 1  

2. Решение:

x – 1 = 1 – x²      или   x – 1 = -(1 – x²)

x² + x – 2 = 0            x² – x = 0

x = -2 или x = 1         x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1. 

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

Пример:

1) |x² – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x² – 5x + 7  = 2x – 5 или x² – 5x +7  = -2x + 5   

x² – 7x + 12  = 0            x² – 3x + 2  = 0

x = 3 или x = 4             x = 2 или x = 1  

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

 x² – 6|x| + 5 = 0. По свойству модуля x² = |x|², поэтому уравнение можно переписать  так:

|x|² – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t² – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1        x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5. 

Рассмотрим еще один пример:

x² + |x| – 2 = 0. По свойству модуля  x² = |x|², поэтому

|x|² + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t² + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2   или |x| = 1

Нет корней     x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

Примеры:

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или  3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5      или     3 + |x + 1| = -5

|x + 1| = 2                       |x + 1| = -8

x + 1 = 2 или x + 1 = -2.   Нет корней.

x = 1            x = -3

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Модуль числа, решение неравенств с модулем, свойства, как раскрыть, чему равен модуль отрицательного числа, как решать уравнения с модулем, примеры графиков

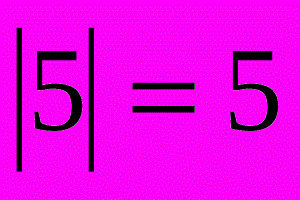
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

1. Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
2. Если абсолютные значения содержат выражения противоположных значений, они равны:
3. Значение числа не превышает величину его модуля:
4. Правило раскрытия при произведении:
5. Правило, применимое при делении:
6. При возведении в степень:
7. Сумма величин:
8. Двойной модуль:

Модуль комплексного числа

Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

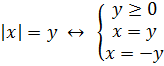
Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке  величина будет отрицательной, а на интервале  будет положительной.

Разделим интервал на 2 части:

1. для x + 2 ≥ 0

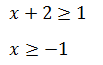
Общим ответом для этих двух неравенств является интервал [−1, + ∞).

2. для х + 2 &lt, 0

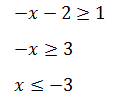
Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

x ∈ (–∞, –3] ∪ [–1, + ∞).

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

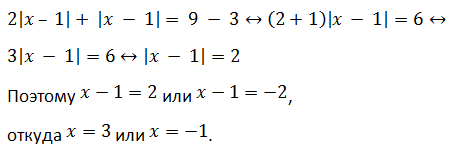
Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

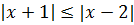
Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

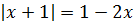
Решение:

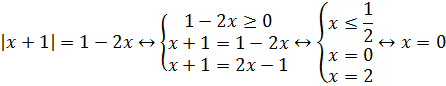
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что  не лежит в промежутке .

Ответ: x = 0.

Модуль суммы

Модуль разности

Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

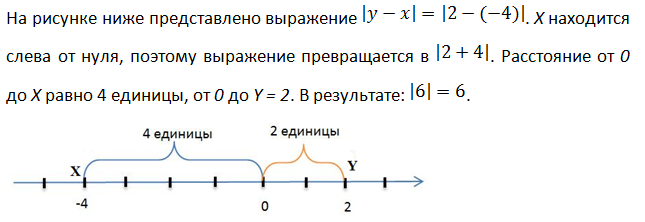
Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

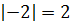
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Известно свойство:

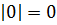
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

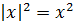
Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

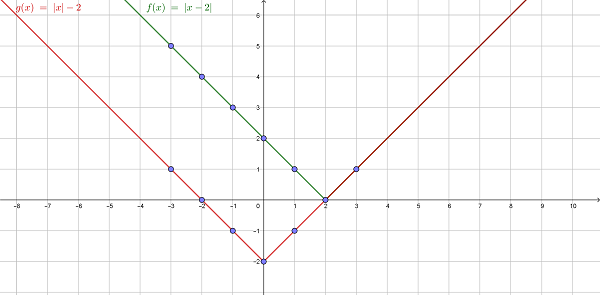
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

Пример 1. Решить методом интервалов.

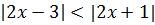
Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

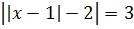
Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

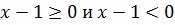
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

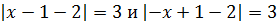
Нужно упростить два уравнения:

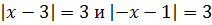
Далее каждое из равенств разделяется еще на два:

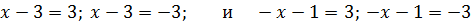
Получено четыре результата:

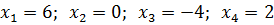
Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него,
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

No related posts.