Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах / Двойной интеграл / 3dstroyproekt.ru
Теорема о замене переменных в двойном интеграле
Пусть на плоскости $\mathbf { \textit { Ouv } } $ задана область $\mathbf { \textit { G } } $, и пусть отображение $\mathbf { \textit { F } } (\mathbf { \textit { M } } )=\mathbf { \textit { M } } $* преобразует эту область в область $\mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Oxy } } . $ Будем считать, что отображение $\mathbf { \textit { F } } $ задаётся функциями
$F:\left[ \begin{array} { l } x=x(u,v) \newline y=y(u,v) \newline \end{array} \right].$
Пусть:
- $\mathbf { \textit { F } } $ взаимно однозначно отображает $\mathbf { \textit { G } } $ на $\mathbf { \textit { D } } $;
- функции $\mathbf { \textit { x } } (\mathbf { \textit { u,v } } )\mathbf { \textit { , y } } (\mathbf { \textit { u,v } } )$ непрерывно дифференцируемы на $\mathbf { \textit { G } } $ { имеют непрерывные частные производные } ;
якобиан $J(u,v)=\frac { \partial (x,y) } { \partial (u,v) } =\left| { \begin{array} { l } \frac { \partial x } { \partial u } \quad \frac { \partial y } { \partial u } \newline \frac { \partial x } { \partial v } \quad \frac { \partial y } { \partial v } \newline \end{array} } \right|$ не обращается в нуль на $\mathbf { \textit { G } } .$
$ { \frac { { \partial \left( { x,y }\right) } } { { \partial \left( { u,v }\right) } } } = { \left| { \begin{array} { * { 20 } { c } } { \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial x } } { { \partial v } } } \\ { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial y } } { { \partial v } } } \end{array} }\right| } = { \left| { \begin{array} { * { 20 } { c } } { \frac { { \partial \left( { u\cos v }\right) } } { { \partial u } } } & { \frac { { \partial \left( { u\cos v }\right) } } { { \partial v } } } \\ { \frac { { \partial \left( { u\sin v }\right) } } { { \partial u } } } & { \frac { { \partial \left( { u\sin v }\right) } } { { \partial v } } } \end{array} }\right| } = { \left| { \begin{array} { * { 20 } { c } } { \cos v } & { — u\sin v } \\ { \sin v } & { u\cos v } \end{array} }\right| } = { \cos v \cdot u\cos v — \left( { — u\sin v }\right) \cdot \sin v } = { u\, { \cos ^2 } v + u\, { \sin ^2 } v } = \\ = { u\left( { { { \cos } ^2 } v + { { \sin } ^2 } v }\right) = u. } $
Докажем, что в этих предположениях $\iint\limits_D { f(x,y)dxdy=\iint\limits_G { f(x(u,v),y(u,v))\cdot \left| { J(u,v) }\right|\cdot dudv } } $.
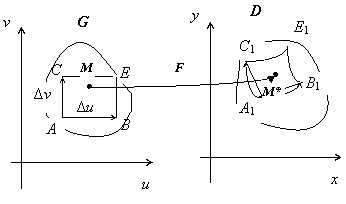
Док-во:
Рассмотрим, как связаны между собой площадь параллелограмма $\mathbf { \textit { АВСЕ } } $ со сторонами $\Delta u,\Delta v $в области $\mathbf { \textit { G } } $ и площадь его образа при преобразовании $\mathbf { \textit { F } } \textbf { — } $криволинейного параллелограмма $\mathbf { \textit { A } } _ { 1 } \mathbf { \textit { B } } _ { 1 } \mathbf { \textit { C } } _ { 1 } \mathbf { \textit { E } } _ { 1 } $ в области $\mathbf { \textit { D } } .$ С точностью до бесконечно малых высших порядков по сравнению с $\Delta u,\Delta v$, площадь криволинейного параллелограмма $\mathbf { \textit { A } } _ { 1 } \mathbf { \textit { B } } _ { 1 } \mathbf { \textit { C } } _ { 1 } \mathbf { \textit { E } } _ { 1 } $ равна площади обычного параллелограмма, построенного на векторах $\overline { A_1 B_1 } $ и $\overline { A_1 C_1 } $. Пусть точка $А$ имеет координаты $\mathbf { \textit { u,v } } $, тогда точка $\mathbf { \textit { А } } _ { 1 } $ будет иметь координаты $\mathbf { \textit { x } } (\mathbf { \textit { u,v } } ),\mathbf { \textit { y } } (\mathbf { \textit { u,v } } ))$, т.е. $A(u,v)\to A_1 (x(u,v),y(u,v))$. Для других точек: $B(u+\Delta u,v)\to B_1 (x(u+\Delta u,v),y(u+\Delta u,v))= \quad B_1 (x(u,v)+\frac { \partial x } { \partial u } (u,v)\Delta u+\alpha _1 (\Delta u)\Delta u,y(u,v)+\frac { \partial y } { \partial u } (u,v)\Delta u+\alpha _2 (\Delta u)\Delta u)$ { по формуле приращения дифференцируемой функции } . Аналогично $C(u,v+\Delta v)\to C_1 (x(u,v+\Delta v),y(u,v+\Delta v))=$
$C_1 (x(u,v)+\frac { \partial x } { \partial v } (u,v)\Delta v+\alpha _3 (\Delta v)\Delta v,y(u,v)+\frac { \partial y } { \partial v } (u,v)\Delta v+\alpha _4 (\Delta v)\Delta v),$ где $\alpha _i \to 0\;(i=1,2,3,4)$ при $\Delta u,\Delta v\to 0$.
Пренебрежём членами порядка малости выше первого по сравнению с $\Delta u,\Delta v$. Тогда $ \overline { AB } [\Delta u,0]\to \overline { A_1 B_1 } \left[ { \frac { \partial x } { \partial u } (u,v),\frac { \partial y } { \partial u } (u,v) \left. { \begin{array} { l } \newline \newline \end{array} }\right] ; } \right.\overline { AC } [0,\Delta v]\to \overline { A_1 C_1 } \left[ { \frac { \partial x } { \partial v } (u,v),\frac { \partial y } { \partial v } (u,v)\left. { \begin{array} { l } \newline \newline \end{array} } \right] } \right. $
Пусть теперь $\textbf { i,j,k } $ — базисные орты пространства, в котором лежит плоскость $\mathbf { \textit { Oxy } } $. Как известно, площадь параллелограмма, построенного на векторах $\overline { A_1 B_1 } $ и $\overline { A_1 C_1 } $, равна модулю векторного произведения этих векторов { проекции на орт $\textbf { k } $равны нулю } : $$ S_ { A_1 B_1 C_1 E_1 } =\left| { \left[ { \overline { A_1 B_1 } \ast \overline { A_1 C_1 } }\right] }\right|=\left| { \left| { \begin{array} { l } { \rm { \bf i } } \quad \;\;\;\;\;\; { \rm { \bf j } } \quad \;\;\;\; { \rm { \bf k } } \newline \frac { \partial x } { \partial u } \Delta u\;\;\frac { \partial y } { \partial u } \Delta u\;\;0 \newline \frac { \partial x } { \partial v } \Delta v\;\;\frac { \partial y } { \partial v } \Delta v\;\;0 \newline \end{array} }\right| }\right|=\left| { \rm { \bf k } }\right|\left| { \left| { \begin{array} { l } \frac { \partial x } { \partial u } \Delta u\;\;\frac { \partial y } { \partial u } \Delta u \newline \frac { \partial x } { \partial v } \Delta v\;\;\frac { \partial y } { \partial v } \Delta v \newline \end{array} }\right| }\right|=\left| { \left| { \begin{array} { l } \frac { \partial x } { \partial u } \;\;\frac { \partial y } { \partial u } \newline \frac { \partial x } { \partial v } \;\;\frac { \partial y } { \partial v } \newline \end{array} }\right| }\right|\left| { \Delta u\Delta v }\right|=\left| { J(u,v) }\right|S_ { ABCE } . $$
Мы доказали замечательную вещь. Если вокруг точки $M\in G$ взять маленькую область, то после преобразования $\mathbf { \textit { F } } $ площадь этой области меняется в $\vert \quad \mathbf { \textit { J } } (\mathbf { \textit { M } } ) \quad \vert $ раз.
- Перейдём к доказательству основной формулы. Разобьём $\mathbf { \textit { G } } $ прямыми, параллельными осям координат, на области $\mathbf { \textit { G } } _ { 1 } $, $\mathbf { \textit { G } } _ { 2 } , { \ldots } , \mathbf { \textit { G } } _ { n } $. Образы этих линий дадут разбиение $\mathbf { \textit { D } } $ на области $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } , { \ldots } , \mathbf { \textit { D } } _ { n } $. Для этого разбиения составим интегральную cумму $\sum\limits_ { i=1 } ^n { f(P_i )S(D_i )= } \sum\limits_ { i=1 } ^n { f(x(u_i ,v_i ),y(u_i ,v_i ))\left| J \right|S(G_i ) } $. Устремим $\mathop { \max } \limits_ { i=1,2,…,n } diam(G_i )\to 0$; тогда и $\mathop { \max } \limits_ { i=1,2,…,n } diam(D_i )\to 0$. И слева, и справа интегральные суммы записаны для непрерывных функций, следовательно,и слева, и справа существуют пределы — двойные интегралы, и они равны: $\iint\limits_D { f(x,y)dxdy=\iint\limits_G { f(u,v)\cdot \left| { J(u,v) }\right|\cdot dudv } } $, что и требовалось доказать.
Двойной интеграл в полярных координатах
Нам придётся применять эту формулу, в основном, для перехода к полярным координатам. Роль переменных $\mathbf { \textit { u } } $ и $\mathbf { \textit { v } } $ будут играть $\mathbf { \textit { r } } $ и $\phi $. Как известно, $x=r\cos \varphi ,y=r\sin \varphi $. Вычислим якобиан: $J=\left| { \left| { \begin{array} { l } \cos \varphi \quad \;\;\;\;\sin \varphi \newline -r\sin \varphi \;\;r\cos \varphi \newline \end{array} }\right| }\right|=\vert r\vert =r$, следовательно, $\iint\limits_ { D(x,y) } { f(x,y)dxdy } =\iint\limits_ { D(r,\phi ) } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } $. Двойной интеграл в координатах $\mathbf { \textit { r } } ,\phi $ вычисляется также как и в координатах $\mathbf { \textit { x } } ,\mathbf { \textit { y } } , $переходом к двухкратному, при этом внешний обычно берут по $\varphi $. Если область $\mathbf { \textit { D } } $ описывается как $D:\left[ { \begin{array} { l } \varphi _0 \leqslant \varphi \leqslant \varphi _k \newline r_1 (\varphi )\leqslant r\leqslant r_2 (\varphi ) \newline \end{array} } \right]$, то $\iint\limits_ { D(r,\varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\int\limits_ { \varphi _0 } ^ { \varphi _k } { d\varphi \int\limits_ { r_1 (\varphi ) } ^ { r_2 (\varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdr } } $. Естественно, если $r_1 (\varphi ),r_2 (\varphi )$ — кусочные функции, то внешний интеграл разбивается на несколько слагаемых. Однозначно дать рецепт, когда имеет смысл переходить к полярным координатам, нельзя, это дело опыта. Можно пробовать перейти к $\mathbf { \textit { r } } ,\phi $, если либо $\mathbf { \textit { f } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } )$, либо кривые, ограничивающие область интегрирования, либо и то, и другое вместе, зависят от комбинации $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $. Если $f(x,y)=f\left( { \frac { x^2 } { a^2 } +\frac { y^2 } { b^2 } }\right)$ и/или область $\mathbf { \textit { D } } $ ограничивается эллипсом $\frac { x^2 } { a^2 } +\frac { y^2 } { b^2 } =1$, полезны обобщённые полярные координаты $x=ar\cos \varphi ,y=br\sin \varphi $. Каков якобиан этого преобразования?
3dstroyproekt.ru
7.5. Двойной интеграл в полярной системе координат
Для
того чтобы двойной интеграл в декартовых
координатах 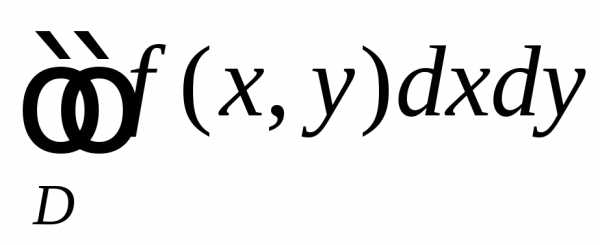 преобразовать в двойной интеграл в
полярных координатах, нужно в
подинтегральной функции заменить,,
а элемент площадизаменить его выражением в полярных
координатах.
преобразовать в двойной интеграл в
полярных координатах, нужно в
подинтегральной функции заменить,,
а элемент площадизаменить его выражением в полярных
координатах.
●Правило расстановки пределов интегрирования (рис. 38)
1. Внутренний интеграл всегда за-висит от переменной ρ, считая φ постоянной величиной.
2. Чтобы расставить пределы внут-реннего интеграла, надо провести лучи,
исходящие
из полюса. Точки входа и точки выхода
лучей в область D,
заданную системой неравенств:  определяют соответствен-но
нижний
и верхнийпределы интегрирования.
определяют соответствен-но
нижний
и верхнийпределы интегрирования.
 и
и ,
считая против хода часовой стрелки (в
положительном направлении).
,
считая против хода часовой стрелки (в
положительном направлении). 4.
Если полюс содержится внутри области D,
то нижний предел внутреннего интеграла
следует положить 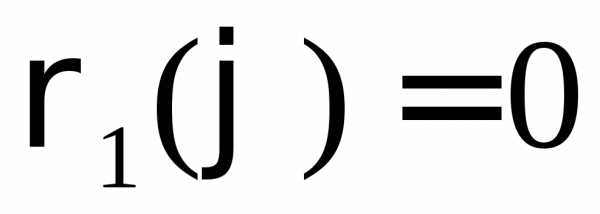 .
Итак,
.
Итак,
.
Замечания.
1. Пределы интегрирования будут постоянными, если область интегрирования представляет собой часть круга.
2. К полярным координатам удобно переходить в том случае, когда область интегрирования ограничена дугами окружностей или линиями, заданными в полярных координатах.
Пример.
Вычислить 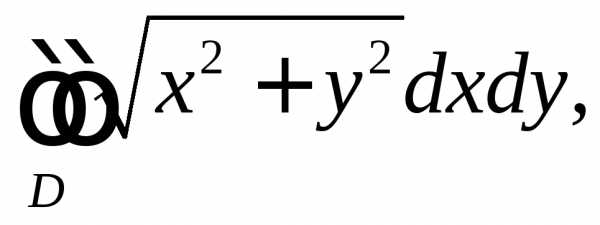 где
где
Решение. Перейдем к полярным координатам:
По
условию задачи
следовательно,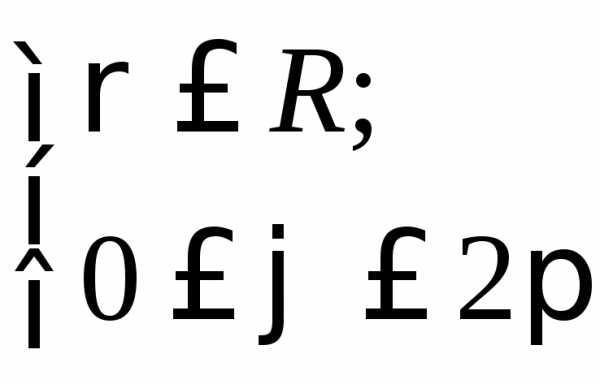 .
Итак,
.
Итак,
7.6. Тройной интеграл
По
аналогии с двойным интегралом вводится
понятие тройного интеграла по ограниченной
замкнутой пространственной области V,
если в ней определена непрерывная
функция
,
который обозначается так:.
Предположим, что областьV является стандартной в направлении оси 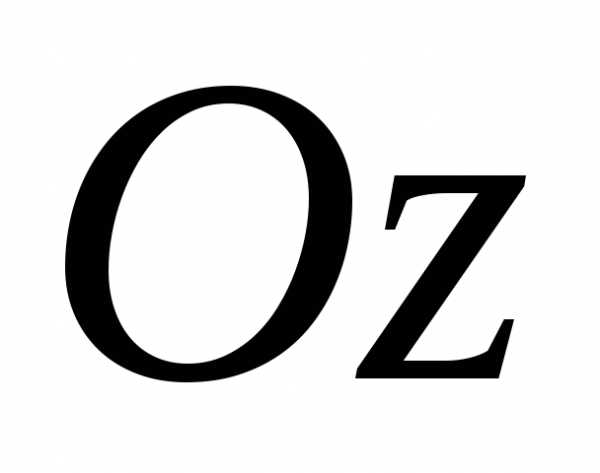 ,
т. е. удовлетворяющей следующим условиям:
,
т. е. удовлетворяющей следующим условиям:
1)
всякая прямая, параллельная оси 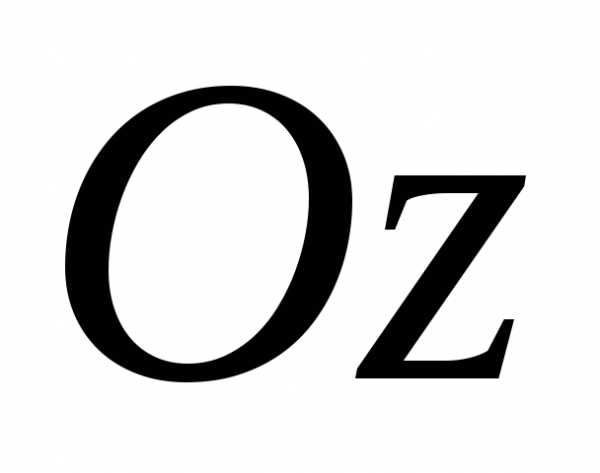 и имеющая с областьюV общие точки, пересекает границу области
только в двух точках;
и имеющая с областьюV общие точки, пересекает границу области
только в двух точках;
2
Рис. 39
) проекцияD области V на плоскость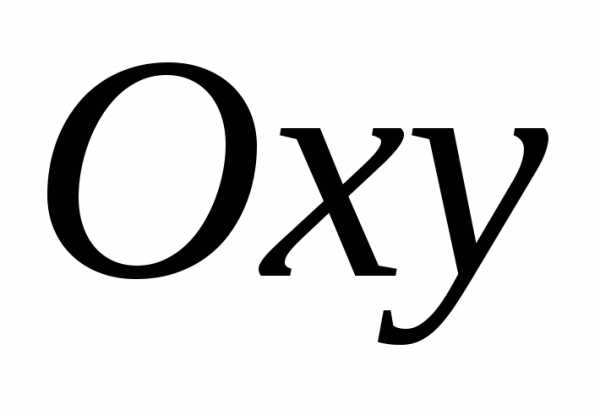
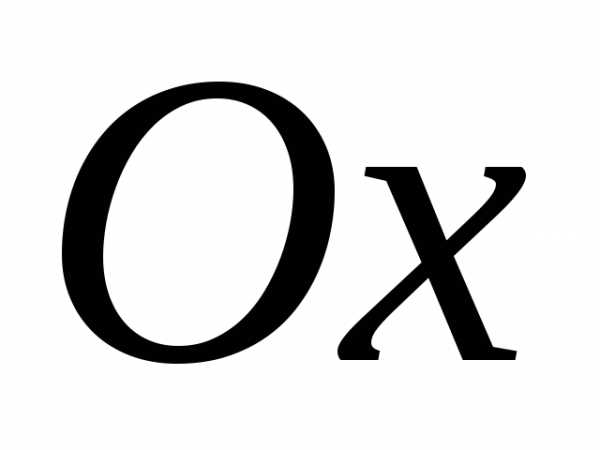 или оси
или оси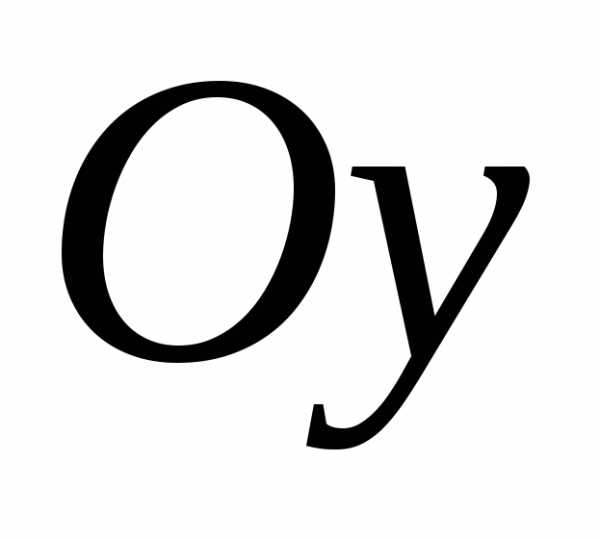 .
.Если при этом область V ограничена сверху поверхностью , а снизу – поверхностью, то тройной интеграл в декартовых координатах можно вычислить следующим образом:
.
Если,
например, область D является стандартной в направлении оси 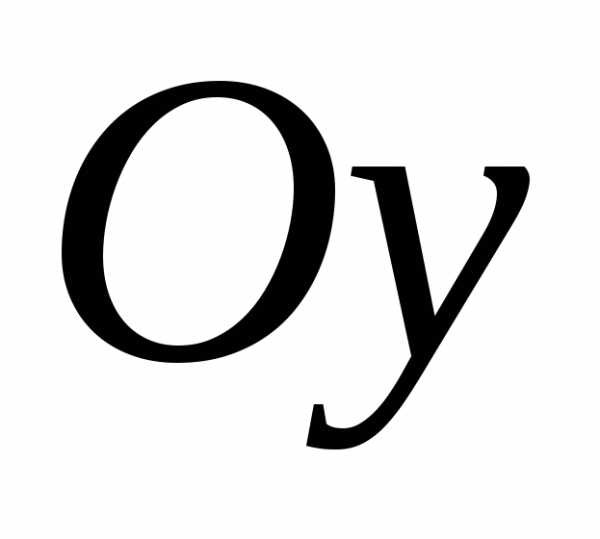 и определяется неравенствами;,
то
и определяется неравенствами;,
то
.
Итак, .
Часто удобно вычисление тройного интеграла провести в цилиндрических или сферических координатах.
Цилиндрические координаты:
,
,
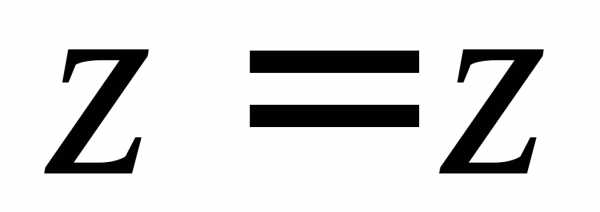
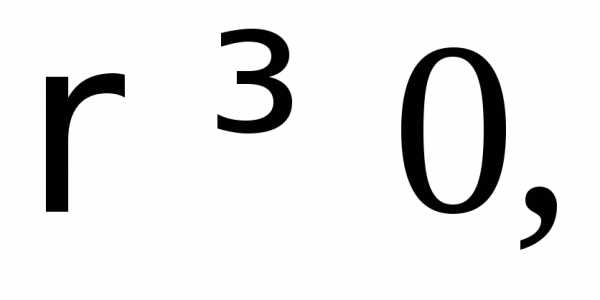
При этом: .
Итак, тройной интеграл в цилиндрических координатах записывается следующим образом:
.
Пример 6.2. Вычислить
Рис. 40
где область V ограничена плоскостями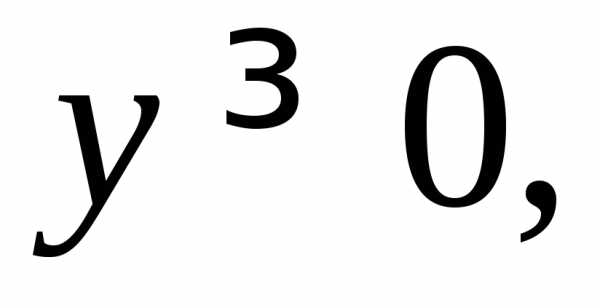
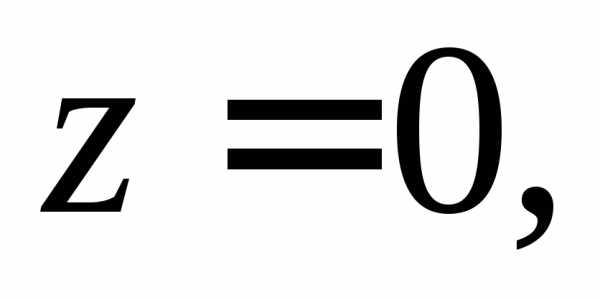
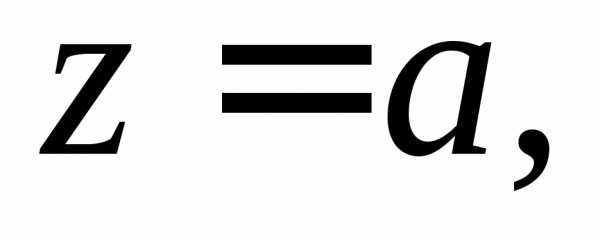 цилиндроми расположена в первом октанте (рис.
40), т. е.
цилиндроми расположена в первом октанте (рис.
40), т. е.
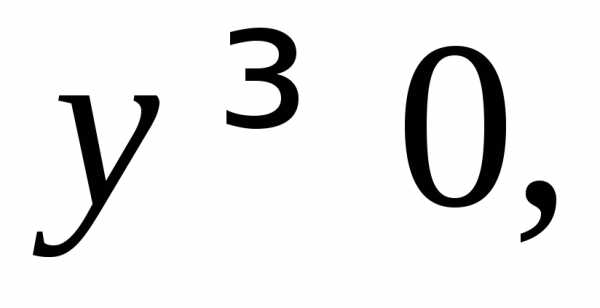
Решение. Вычислим в цилиндрической системе координат
Сферические координаты:
,
,
,
где 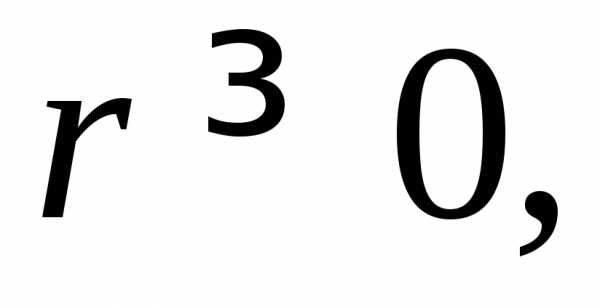
При этом: .
Тройной интеграл в сферических координатах записывается так:
Особенно удобно применение сферических координат в случае, когда область интегрирования V-шap с центром в начале координат или шаровое кольцо.
Пример 6.3. Вычислить
где V – шар, который описывается неравенством (рис. 41).
Р
Рис. 41
ешение. Перейдем к сферическим координатам. При этом подынтегральная функция примет вид . Следовательноstudfiles.net
замена переменной в кратном интеграле. полярные координаты — ПриМат
При вычислении кратных интегралов часто возникает необходимость перейти к более простой области интегрирования для упрощения их вычисления, возможно даже ценой некоторого усложнения подынтегральной функции.
Из курса аналитической геометрии известны следующие соотношения между декартовыми и полярными координатами: $x = r\cos\phi,\quad y = r\sin\phi\quad(*)$.
При этом, $r \geq 0, 0 \leq \phi <2\pi$. Рассмотрим вспомогательную плоскость $RO\Phi$, где $r$ и $\phi$ являются декартовыми координатами, и определим на ней множество точек $G$, такое, что: $G = \{(r, \phi)| r > 0, 0 \leq \phi < 2\pi\}$.
Тогда формулы $(*)$ определяют непрерывно дифференцируемое отображение $F : G \to \widetilde{XOY}$, где $\widetilde{XOY} = XOY \setminus\{(0, 0)\}$.
По определению полярных координат, в декартовой системе координат $XOY$ $r$ задает радиус окружности с центром в начале координат, а $\phi$ определяет луч, исходящий из центра координат, такой что угол между лучом и положительным направлением оси $OX$ равен $\phi$. С геометрической точки зрения очевидно, что они пересекаются в единственной точке.
Таким образом, любую точку $P = (x_0, y_0)$ из $\widetilde{XOY}$ можно однозначно определить пересечением луча, направленного под углом $\phi_0$ и окружности радиусом $r_0$, и тогда точка $P’ = (r_0, \phi_0)$ будет единственным прообразом $P$ в $G$. Очевидно, что любой элемент из $G$ служит прообразом, и что двум различным точкам из $G$ будут соответствовать 2 различные точки из $\widetilde{XOY}$. Таким образом, отображение $F$ между точками плоскостей $G$ и $\widetilde{XOY}$ взаимно однозначное:
Якобиан полученного отображения будет равен:
$J_F = \begin{array}{|cc|} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \phi} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \phi} \end{array} = \begin{array}{|cc|} \cos{\phi}& -r\sin{\phi} \\ \sin{\phi} & r\cos{\phi} \end{array} = r$
Теперь рассмотрим множество точек $G’$, полученное добавлением к множеству $G$ отрезка $r = 0$, т.е. $G’ = \{(r, \phi)| r \geq 0, 0 \leq \phi < 2\pi\}.$ $G’$ уже является прообразом всей плоскости $XOY$, но на отрезке $r = 0, 0 \leq \phi < 2\pi$ не достигается взаимная однозначность, а $\left|J_F\right| = 0$. Обратим внимание, что его Жорданова мера равна нулю.
Наконец, пусть дана область $\Omega \subset XOY$ и функция $f$, непрерывная на измеримом множестве $\overline{\Omega}$. Ее прообразом при отображении $F$, заданного формулами $(*)$, будет некоторая область $\Omega’ \subset G’$. Если область $\Omega$ не содержит точки O — начала координат, то выполнены все условия теоремы о замене переменной в кратных интегралах, и справедлива формула:
$$\iint\limits_{\Omega} f(x, y)\,dxdy = \iint\limits_{\Omega’} f(r\cos{\phi}, r\sin{\phi})r\,drd\phi$$
Если же точка $O \in \Omega$, то взаимная однозначность и не обращение якобиана в нуль не выполняются на множестве $r = 0$, что не влияет на справедливость данной формулы (следует из замечания к указанной теореме).
Пример №1
Вычислить интеграл:
$\iint\limits_{\Omega}(x^2 + y^2)\,dxdy, \Omega = \{(x, y)| y \geq 0, x^2 + y^2 \leq a^2\}.$
Заметим, что в полярных координатах полукруг будет представлять из себя более простую область интегрирования:
Поэтому, воспользуемся формулой замены переменной и перейдем к полярным координатам:
$\iint\limits_{\Omega}(x^2 + y^2)\,dxdy = \iint\limits_{\Omega’}r^2r\,drd\phi = \int\limits_0\limits^{\pi}\,d\phi\int\limits_0\limits^ar^3\,dr = $ $ \int\limits_0\limits^{\pi}\frac{a^4}{4}\,d\phi = \frac{\phi a^4}{4}|_0^{\pi} = \frac{\pi a^4}{4}$.
[свернуть]
Рассмотрим теперь пространство $\mathbb{R}^3$, в котором задана декартова система координат $OXYZ$. Цилиндрические координаты связанны с декартовыми следующим образом:
$x = r\cos\phi,\quad y = r\sin\phi,\quad z = t\quad(**),$
где $r \geq 0, 0 \leq \phi <2\pi, t \in \mathbb{R}$ (величины $r$ и $\phi$ для любой точки $A = (x, y, z)$ определяются таким же образом, как и в полярных координатах для ее проекции $P’ = (x, y, 0)$ на $XOY$). Теперь, аналогично случаю с полярными координатами, рассмотрим вспомогательное пространство $OR\Phi T$, где $r, \phi, t$ — декартовы координаты, а в нем — множество точек $G = \{(r, \phi, t)| r \geq 0, 0 \leq \phi <2\pi, t \in \mathbb{R}\}$.
Отображение $F : G \to OXYZ$, определяемое формулами $(**)$, является непрерывно дифференцируемым.
$J_F = \begin{array}{|ccc|} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \phi} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \phi} & \frac{\partial y}{\partial t} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \phi} & \frac{\partial z}{\partial t} \end{array} = \begin{array}{|ccc|} \cos{\phi}& -r\sin{\phi} & 0 \,\\ \sin{\phi} & r\cos{\phi} & 0 \,\\ 0 & 0 & 1\,\end{array} = r$
Очевидно, что как и в случае с полярными координатами, отображение $F$ — взаимно однозначное, и его якобиан не равен нулю. Данные условия не выполняются только при $r = 0$, т.е. на множестве $L = \{(r, \phi, t)| r = 0, 0 \leq \phi <2\pi, t \in \mathbb{R}\}$. Пересечение такого множества с любым другим ограниченным множеством есть ограниченное линейное множество, и жорданова мера этого пересечения равна нулю.
Тогда, если дана область $\Omega \subset OXYZ$, и функция $f$ непрерывна на измеримом множестве $\overline{\Omega}$, а $\Omega’ \subset G$ — прообраз данной области при отображении $F$, то выполнены все условия теоремы о замене, и справедлива следующая формула:
$$\iiint\limits_{\Omega} f(x, y, z)\,dxdydz = \iiint\limits_{\Omega’} f(r\cos{\phi}, r\sin{\phi}, t)r\,drd\phi dt$$
Наконец, рассмотрим сферические координаты, связанные с декартовыми следующими соотношениями: $x = r\cos{\phi} \cos{\psi},\quad y = r\sin{\phi} \cos{\psi},\quad z = r\sin{\psi}\quad (***),$
где $r \geq 0, 0 \leq \phi < 2\pi, -\frac{\pi}{2} \leq \psi \leq \frac{\pi}{2}$. Введем вспомогательное пространство $OR\Phi\Psi$, где $r, \phi, \psi$ — декартовы координаты, а в нем рассмотрим множество точек $G = \{(r, \phi, \psi)| r \geq 0, 0 \leq \phi < 2\pi -\frac{\pi}{2} \leq \psi \leq \frac{\pi}{2}\}$.
Отображение $F : G \to OXYZ$, определяемое формулами $(***)$, непрерывно дифференцируемо.
$J_F = \begin{array}{|ccc|} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \phi} & \frac{\partial x}{\partial \psi} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \phi} & \frac{\partial y}{\partial \psi} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \phi} & \frac{\partial z}{\partial \psi} \end{array} = \begin{array}{|ccc|} \cos{\phi}\cos{\psi}& -r\sin{\phi}\cos{\psi} & -r\cos{\phi}\sin{\psi} \,\\ \sin{\phi}\cos{\psi} & r\cos{\phi}\cos{\psi} & -r\sin{\phi}\sin{\psi} \,\\ \sin{\psi} & 0 & r\cos{\psi}\,\end{array} = $ $ r^2\cos{\psi}$.
Взаимная однозначность данного отображения устанавливается по тем же рассуждениям, что и в предыдущих двух случаях, и не выполняется только при $r = 0, \psi = -\frac{\pi}{2}, \psi = \frac{\pi}{2}$, когда и якобиан равен нулю. Однако любое подмножество множества, задаваемого такими равенствами, будет представлять собой ограниченную часть плоскости с жордановой мерой нуль в пространстве $OXYZ$, что не помешает совершить замену.
Тогда, при соответствующих условиях, справедлива формула замены переменной ($\Omega \subset OXYZ, \Omega’ \subset G$):
$$\iiint\limits_{\Omega} f(x, y, z)\,dxdydz = $$ $$\iiint\limits_{\Omega’} f(r\cos{\phi}\cos{\psi}, r\sin{\phi}\cos{\psi}, r\sin{\psi})r^2\cos{\psi}\,drd\phi d\psi$$
Пример №2
Вычислить интеграл $\iiint\limits_{\Omega} e^{{(x^2 + y^2 + z^2)}^{\frac{3}{2}}}\,dxdydz$, где граница области $\Omega$ задается уравнением $x^2 + y^2 + z^2 = 1$.
Область интегрирования представляет собой шар радиуса с центром в начале координат. Следовательно, будет удобно воспользоваться переходом к цилиндрической системе координат. В ней новая область интегрирования будет определятся следующими неравенствами: $0 \leq \phi \leq 2\pi,\quad -\frac{\pi}{2} \leq \psi \leq \frac{\pi}{2},\quad 0 \leq r \leq 1$. Воспользуемся формулой замены переменной для сферических координат:
$\iiint\limits_\Omega e^{(x^2 + y^2 + z^2)^{\frac{3}{2}}}\,dxdydz = $ $\iiint\limits_{\Omega’} e^{r^{2^{\frac{3}{2}}}}r^2\cos{\psi} \,drd\phi d\psi = \int\limits_0\limits^{2\pi}\,d\phi\int\limits_0\limits^1e^{r^3}r^2\,dr\int\limits_{-\frac{\pi}{2}}\limits^{\frac{\pi}{2}}\cos{\psi}\,d\psi = $ $\int\limits_0\limits^{2\pi}\,d\phi\int\limits_0\limits^1e^{r^3}r^2\,dr \cdot (\sin{\psi})|_{-\frac{\pi}{2}}^{\frac{\pi}{2}} = 2\int\limits_0\limits^{2\pi}\,d\phi\int\limits_0\limits^1\frac{1}{3}e^{r^3}\,d(r^3) = $ $\frac{2}{3}\int\limits_0\limits^{2\pi}\,d\phi \cdot e^{r^3}|_0^1 = \frac{2}{3}(e — 1)\int\limits_0\limits^{2\pi}\,d\phi = \frac{2}{3}(e — 1) \cdot \phi|_0^{2\pi} = \frac{4\pi}{3}(e — 1)$
[свернуть]
Лимит времени: 0
Информация
Тест: Использование полярных, цилиндрических и сферических координат для вычисления кратных интегралов
Для закрепления материала, рекомендуется пройти тест по данной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
Задание 1 из 5
Сопоставьте каждой системе координат якобиан, соответствующий переходу из декартовой системы координат в данную.
- $J_F = \begin{array}{|cc|} \cos{\phi}& -r\sin{\phi}\, \\ \sin{\phi} & r\cos{\phi}\, \end{array}$
- $J_F = \begin{array}{|ccc|} \cos{\phi}& -r\sin{\phi} & 0\, \\ \sin{\phi} & r\cos{\phi} & 0\, \\ 0 & 0 & 1\,\end{array}$
- $J_F = \begin{array}{|ccc|} \cos{\phi}\cos{\psi}& -r\sin{\phi}\cos{\psi} & -r\cos{\phi}\sin{\psi} \,\\ \sin{\phi}\cos{\psi} & r\cos{\phi}\cos{\psi} & -r\sin{\phi}\sin{\psi} \,\\ \sin{\psi} & 0 & r\cos{\psi}\,\end{array}$
Полярные координаты
Цилиндрические координаты
Сферические координаты
Задание 2 из 5
Пусть $R$ — заданная область интегрирования в декартовых координатах, а $S$ — область интегрирования, получаемая при переходе к полярным координатам. В каких формулах замена переменных при переходе к полярным координатам была выполнена правильно?
Задание 3 из 5
Расположите данные интегралы в порядке возрастания их значений (для вычисления каждого из них воспользуйтесь переходом к цилиндрическим, сферическим или полярным координатам).
$\iint\limits_U {xy\,dydx}, U: 1 \leq x^2 + y^2 \leq 5$
$\iiint\limits_U {\left( {{x^4} + 2{x^2}{y^2} + {y^4}} \right)\,dxdydz} , U: 0 \leq z \leq 1, x^2 + y^2 \leq 1$
$\iiint\limits_U {\sqrt {{x^2} + {y^2} + {z^2}}\,dxdydz}, U: x^2 + y^2 + z^2 \leq 25$
Задание 4 из 5
Переход к каким координатам (полярным, сферическим или цилиндрическим) наиболее упростит вычисление интеграла $\iiint\limits_U {\left( {{x^4} + 2{x^2}{y^2} + {y^4}} \right)\,dxdydz},$ где область $U$ задается следующим образом: $x^2+y^2 \leq 1, 0 \leq z \leq 1?$
Задание 5 из 5
Вычислите c помощью перехода к полярным координатам интеграл $\iint\limits_Uxy^2\,dxdy,$ $U = \{(x, y)| 4 \leq x^2 + y^2 \leq 16, x \geq 0, y \leq 0\}.$ Для обозначения деления используйте символ «/», для обозначения числа $\pi$ — «pi».
Таблица лучших: Переход к полярным, цилиндрическим и сферическим координатам при вычислении кратных интегралов
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
ib.mazurok.com
7.5. Двойной интеграл в полярной системе координат
Для
того чтобы двойной интеграл в декартовых
координатах 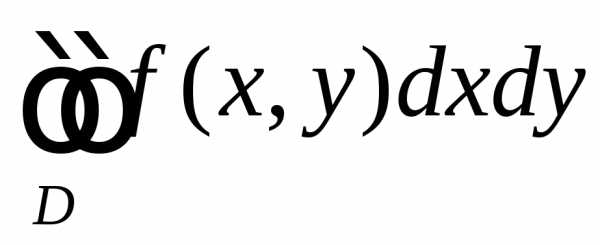 преобразовать в двойной интеграл в
полярных координатах, нужно в
подинтегральной функции заменить,,
а элемент площадизаменить его выражением в полярных
координатах.
преобразовать в двойной интеграл в
полярных координатах, нужно в
подинтегральной функции заменить,,
а элемент площадизаменить его выражением в полярных
координатах.
●Правило расстановки пределов интегрирования (рис. 38)
1. Внутренний интеграл всегда за-висит от переменной ρ, считая φ постоянной величиной.
2. Чтобы расставить пределы внут-реннего интеграла, надо провести лучи,
исходящие
из полюса. Точки входа и точки выхода
лучей в область D,
заданную системой неравенств:  определяют соответствен-но
нижний
и верхнийпределы интегрирования.
определяют соответствен-но
нижний
и верхнийпределы интегрирования.
3.
Пределы внешнего интеграла определяются
уравнениями лучей  и
и ,
считая против хода часовой стрелки (в
положительном направлении).
,
считая против хода часовой стрелки (в
положительном направлении).
4.
Если полюс содержится внутри области D,
то нижний предел внутреннего интеграла
следует положить 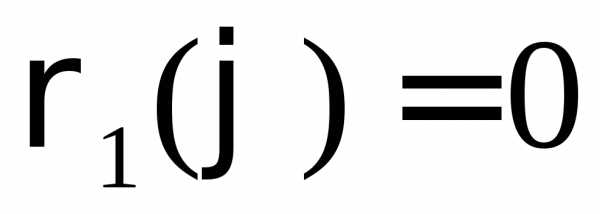 .
Итак,
.
Итак,
.
Замечания.
1. Пределы интегрирования будут постоянными, если область интегрирования представляет собой часть круга.
2. К полярным координатам удобно переходить в том случае, когда область интегрирования ограничена дугами окружностей или линиями, заданными в полярных координатах.
Пример.
Вычислить 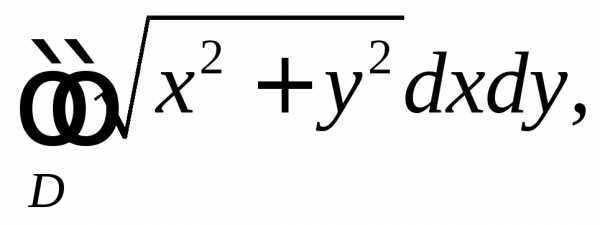 где
где
Решение. Перейдем к полярным координатам:
По
условию задачи
следовательно,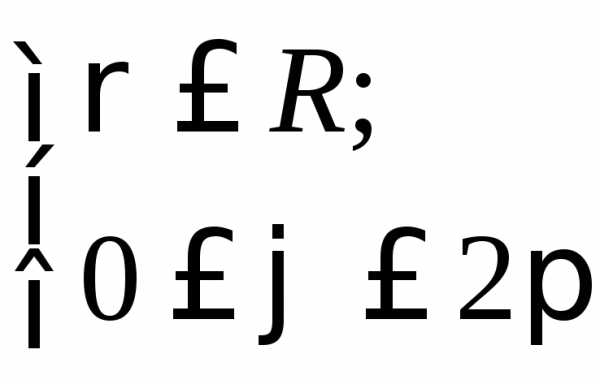 .
Итак,
.
Итак,
7.6. Тройной интеграл
По
аналогии с двойным интегралом вводится
понятие тройного интеграла по ограниченной
замкнутой пространственной области V,
если в ней определена непрерывная
функция
,
который обозначается так:.
Предположим, что областьV является стандартной в направлении оси 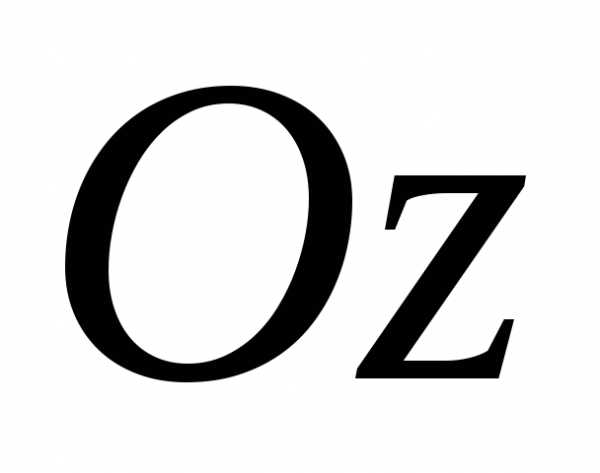 ,
т. е. удовлетворяющей следующим условиям:
,
т. е. удовлетворяющей следующим условиям:
1)
всякая прямая, параллельная оси 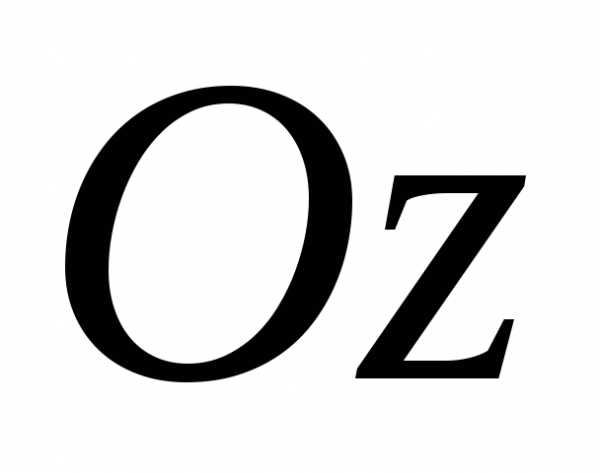 и имеющая с областьюV общие точки, пересекает границу области
только в двух точках;
и имеющая с областьюV общие точки, пересекает границу области
только в двух точках;
2
Рис. 39
) проекцияD области V на плоскость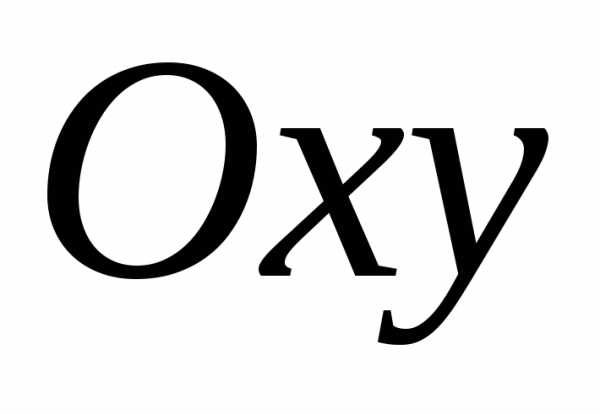 представляет стандартную область в
направлении оси
представляет стандартную область в
направлении оси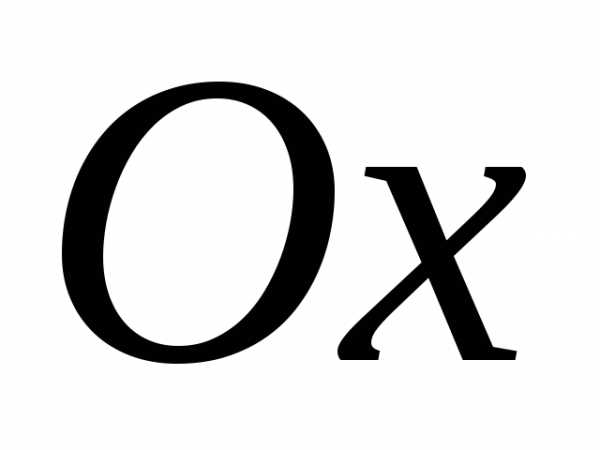 или оси
или оси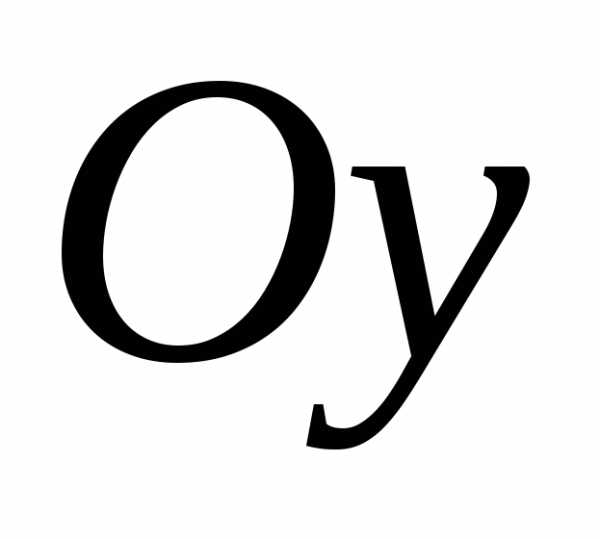 .
.Если при этом область V ограничена сверху поверхностью , а снизу – поверхностью, то тройной интеграл в декартовых координатах можно вычислить следующим образом:
.
Если,
например, область D является стандартной в направлении оси 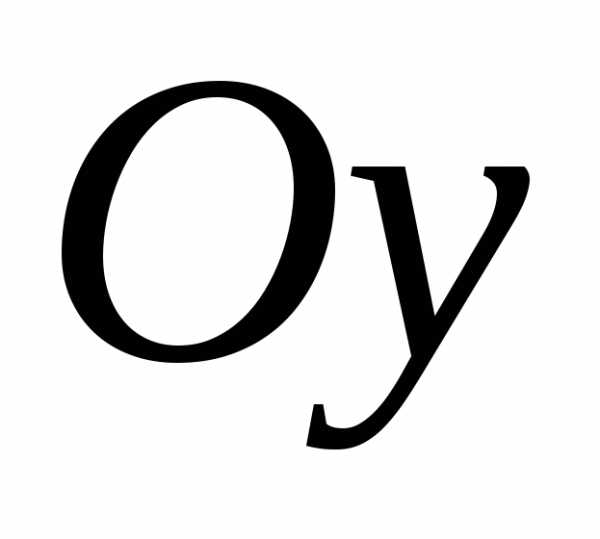 и определяется неравенствами;,
то
и определяется неравенствами;,
то
.
Итак, .
Часто удобно вычисление тройного интеграла провести в цилиндрических или сферических координатах.
Цилиндрические координаты:
,
,
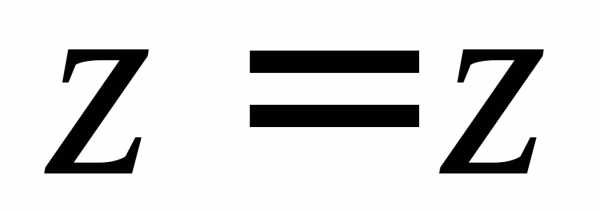 ,
где
,
где 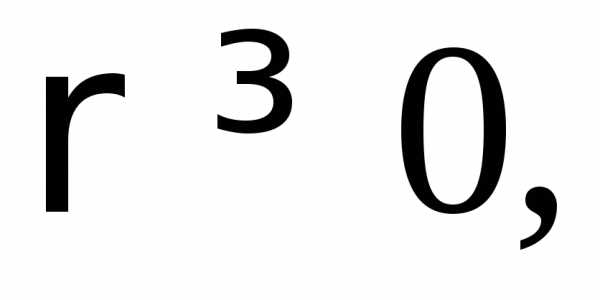
При этом: .
Итак, тройной интеграл в цилиндрических координатах записывается следующим образом:
.
Пример 6.2. Вычислить
Рис. 40
где область V ограничена плоскостями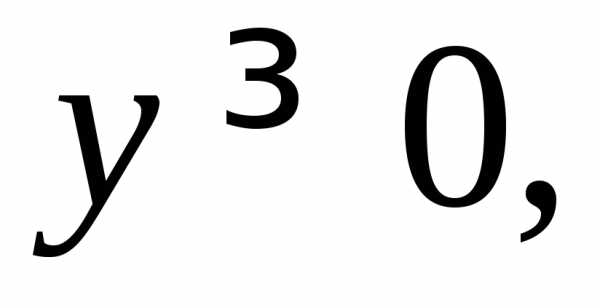
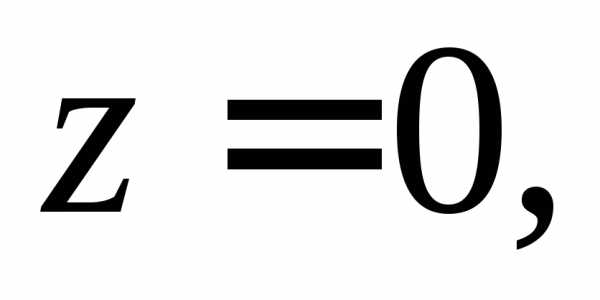
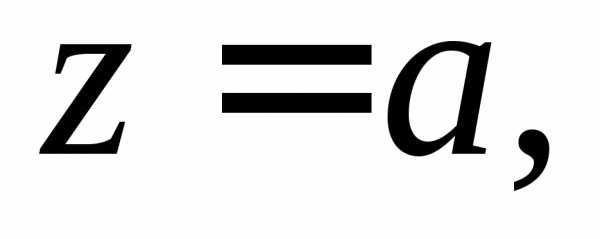 цилиндроми расположена в первом октанте (рис.
40), т. е.
цилиндроми расположена в первом октанте (рис.
40), т. е.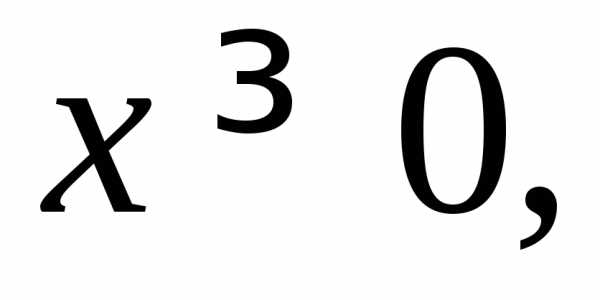
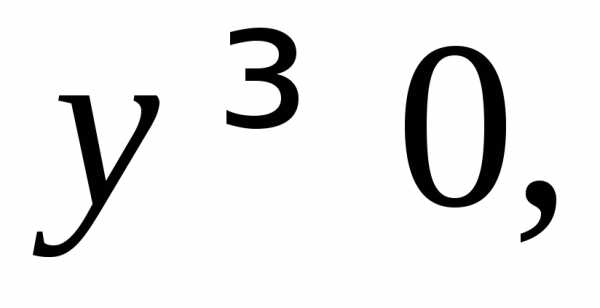
Решение. Вычислим в цилиндрической системе координат
Сферические координаты:
,
,
,
где 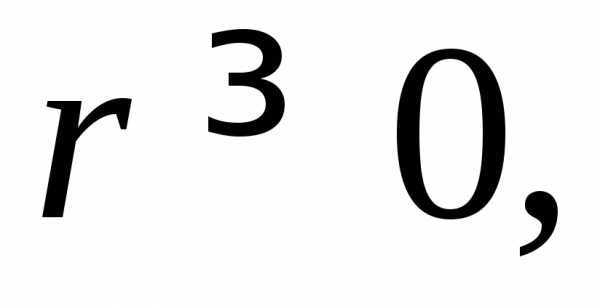
При этом: .
Тройной интеграл в сферических координатах записывается так:
Особенно удобно применение сферических координат в случае, когда область интегрирования V-шap с центром в начале координат или шаровое кольцо.
Пример 6.3. Вычислить
где V – шар, который описывается неравенством (рис. 41).
Р
Рис. 41
ешение. Перейдем к сферическим координатам. При этом подынтегральная функция примет вид . Следовательноstudfiles.net
3. Вычисление двойного интеграла в полярных координатах
Введем на плоскости криволинейную систему координат, называемую полярной. Она состоит из точки О (полюса) и выходящего из него луча (полярной оси).
Рис. 6 Рис. 7
Координатами точки М в этой системе (рис. 6) будут длина отрезка МО – полярный радиус ρ и угол φ между МО и полярной осью: М(ρ,φ). Отметим, что для всех точек плоскости, кроме полюса, ρ > 0, а полярный угол φ будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.
Замечание. Если ограничить значения φ интервалом [0,2π] или [-π, π], то каждой точке плоскости соответствует единственная пара координат (ρ,φ). В других случаях можно считать, что φ может принимать любые значения, то есть полярный угол определяется с точностью до слагаемого, кратного 2π.
Связь между
полярными и декартовыми координатами
точки М можно задать, если совместить начало
декартовой системы координат с полюсом,
а положительную полуось Ох – с полярной осью (рис. 7). Тогда x=ρcosφ, у=ρsinφ
. Отсюда
,tg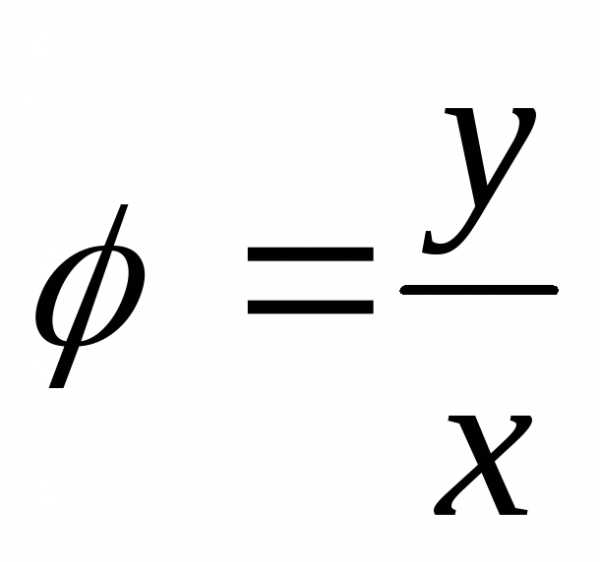 .
.
Правильной областью в полярных координатах назовем такую область, границу которой каждый луч, выходящий из полюса, пересекает не более чем в двух точках (рис.8).
Зададим в области D, ограниченной кривыми ρ=Φ1 (φ) и ρ=Φ2 (φ), где φ1 < φ < φ2 , непрерывную функцию z = f(φ, ρ) . Разобьем область D на части ΔSik , ограниченные лучами ρ = ρi—1 и ρ = ρi , выходящими из полюса, и дугами окружностей φ = φk-1 и φ = φk с центром в полюсе, и составим интегральную сумму , гдеPik – произвольная точка, принадлежащая ΔSik . Найдем площадь части ΔSik , не пересекаемой границей области, как разность площадей двух секторов:
Рис. 8
,
где
.
Учитывая, что площади частей, пересекаемых
границей области, стремятся к нулю при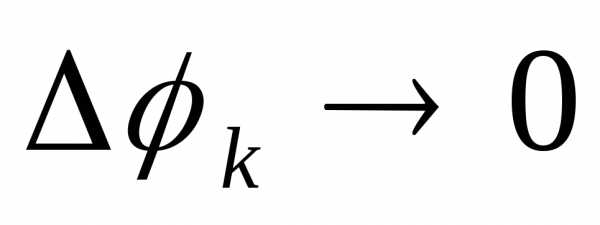 и
и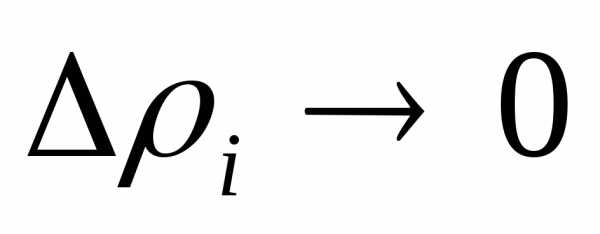 ,
получим:
,
получим:
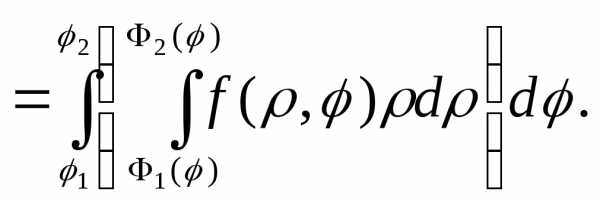 (20)
(20)
Пример 2.
Выведем с использованием двойного интеграла формулу для площади круга радиуса R с центром в начале координат:
Пример 3.
Вычислим, используя полярные координаты, двойной интеграл
,
где D – часть кругового сектора единичного радиуса с центром в начале координат, расположенная в 1-м квадранте.
Заданный интеграл
в полярных координатах 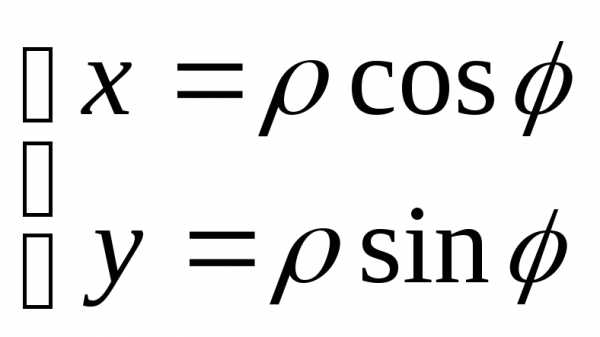 по указанной области
по указанной области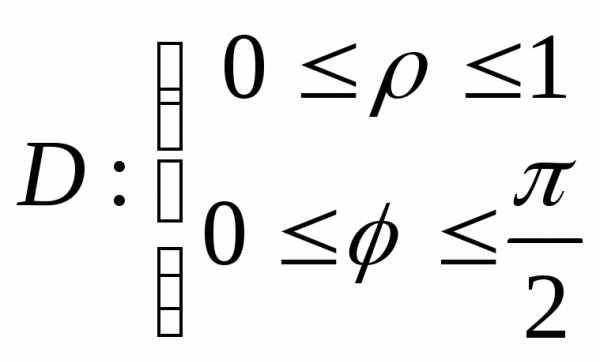 имеет вид:
имеет вид:
4. Вычисление тройного интеграла
в декартовых координатах
Процедура вычисления тройного интеграла аналогична соответствующей операции для двойного интеграла. Для ее описания введем понятие правильной трехмерной области:
Определение 4. Трехмерная область V, ограниченная замкнутой поверхностью S, называется правильной, если:
любая прямая, параллельная оси Оz и проведенная через внутреннюю точку области, пересекает S в двух точках;
вся область V проектируется на плоскость Оху в правильную двумерную область D;
любая часть области V, отсеченная от нее плоскостью, параллельной какой-либо из координатных плоскостей, обладает свойствами 1) и 2).
Рассмотрим правильную область V, ограниченную снизу и сверху поверхностями z=χ(x,y) и z=ψ(x,y) и проектирующуюся на плоскость Оху в правильную область D, внутри которой х изменяется в пределах от а до b, ограниченную кривыми y=φ1(x) и y=φ2(x) (рис.9). Зададим в области V непрерывную функцию f(x, y, z).
Определение 5. Назовем трехкратным интегралом от функции
f(x, y, z) по области V выражение вида:
. (21)
Рис.9.
Трехкратный интеграл обладает теми же свойствами, что и двукратный. Перечислим их без доказательства, так как они доказываются аналогично случаю двукратного интеграла.
Если область V разбить на две области V1 и V2 плоскостью, параллельной какой-либо из координатных плоскостей, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2.
Если т и М – соответственно наименьшее и наибольшее значения функции f(x,y,z) в области V, то верно неравенство . mV ≤ IV ≤ MV, где V – объем данной области, а IV – трехкратный интеграл от функции f(x,y,z) по области V.
Трехкратный интеграл IV от непрерывной функции f(x,y,z) по области V равен произведению его объема V на значение функции в некоторой точке Р области V (теорема о среднем): (22)
Теорема 3. Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области:
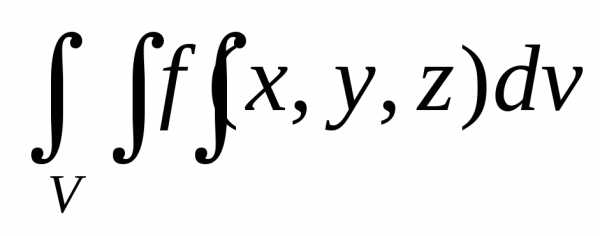 .
(23)
.
(23)
Доказательство.
Разобьем область V плоскостями, параллельными координатным плоскостям, на п правильных областей . Тогда из свойства 1 следует, что
,
где  — трехкратный интеграл от функцииf(x,y,z) по области
— трехкратный интеграл от функцииf(x,y,z) по области 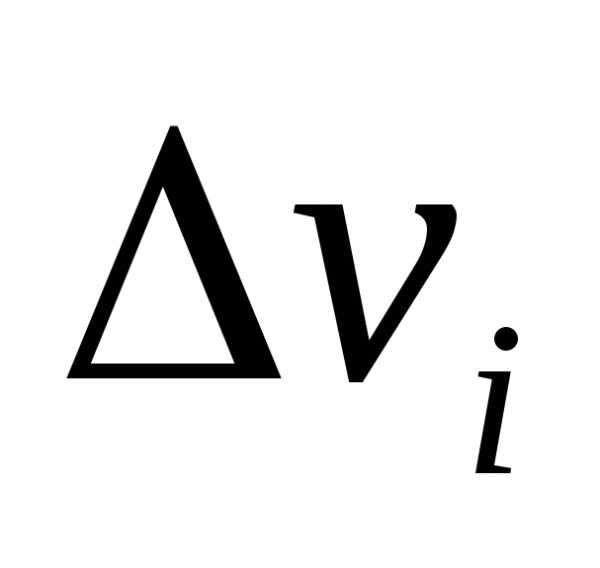 .
.
Используя формулу (21), предыдущее равенство можно переписать в виде:
.
Из условия
непрерывности функции f(x,y,z) следует, что предел интегральной суммы,
стоящей в правой части этого равенства,
существует и равен тройному интегралу 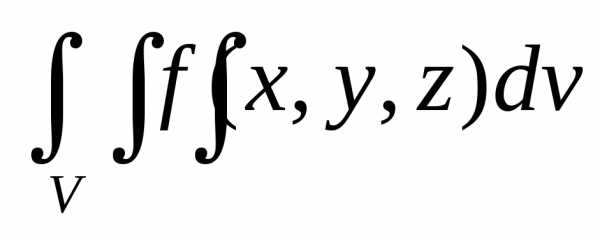 . Тогда,
переходя к пределу при
. Тогда,
переходя к пределу при 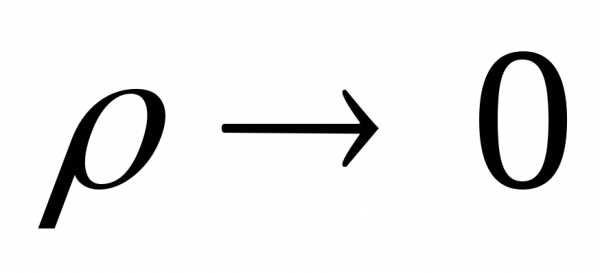 ,
получим:
,
получим:
IV = 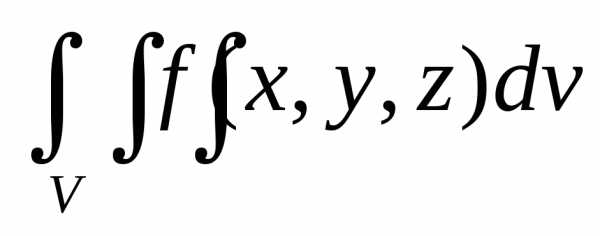 ,
,
что и требовалось доказать.
Замечание.
Аналогично случаю двойного интеграла можно доказать, что изменение порядка интегрирования не меняет значения трехкратного интеграла.
Пример 4.
Вычислим интеграл 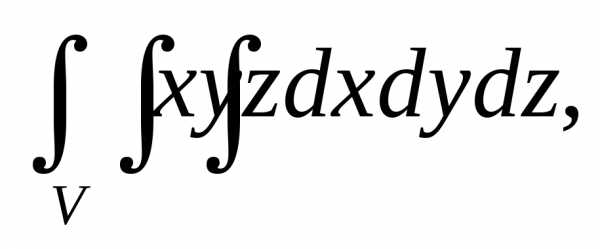 гдеV – треугольная
пирамида с вершинами в точках (0, 0, 0), (1,
0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость
Оху является треугольник с вершинами (0, 0),
(1, 0) и (0, 1). Снизу область ограничена
плоскостью z = 0, а сверху
– плоскостью x + y + z = 1. Перейдем
к трехкратному интегралу:
гдеV – треугольная
пирамида с вершинами в точках (0, 0, 0), (1,
0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость
Оху является треугольник с вершинами (0, 0),
(1, 0) и (0, 1). Снизу область ограничена
плоскостью z = 0, а сверху
– плоскостью x + y + z = 1. Перейдем
к трехкратному интегралу:
Множители, не зависящие от переменной интегрирования, можно вынести за знак соответствующего интеграла:
studfiles.net
Замена в двойном интеграле. Полярные координаты.
Кроме пары чисел , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим . Угол между осью и этим отрезком обозначим .
Так как это прилежащий катет, а гипотенуза, тогда , аналогично , откуда следуют такие формулы:
Также возможен обратный пересчёт: , а угол: (это верно для 4 и 1 четвертей, то есть там, где основная непрерывная ветвь тангенса) и для 2,3 четвертей.
Полярная система фактически применяется в жизни, например в городах с радиальной сеткой улиц. Так, в Москве есть юго-западный округ, северо-восточный и т.д. То есть там практически важно расстояние от центра (Кремля) и направление от центра (на юг, запад, восток, северо-запад и т.д.).
При замене переменных, соответственно, надо все переменные , присутствующие в функции, заменить на , а все на , то есть получим . Однако необходимо ещё заменить дифференциал, если помните, в 1-мерном случае это делали так: например, при было . В двумерном случае, дополнительный множитель также есть. Если бы просто написали вместо , то неверно задали бы искажение сетки координат при замене. Еслди изобразить дуги и радиусы, то сектора круга сужаются к центру, а когда переносим изображение в плоскость параметров то мы растягиваем эту сетку на некоторый прямоугольник, зелёный сектор по площади гораздо меньше красного, но без правильного пересчёта дифференциалов они получились бы равны. Чертёж — слева в плоскости параметров , справа в плоскости .
При том же растворе угла, чем ближе сектор к центру, тем меньше его площадь, и соответственно, меньше его влияние на интеграл. Для правильного учёта этих искажений, надо умножить на определитель матрицы линейного оператора порядка 2, эта матрица в то же время и является производной матрицей отображения .
При замене двух старых на две новые переменные в плоскости, существует уже 4 различных частных производных, и из них можно образовать матрицу 2-го порядка. Строение этой матрицы: .
Она называется матрицей Якоби, а её определитель — определителем Якоби, или «якобианом». В данном случае,
= , определитель: = .
Итак, доказали, что определитель Якоби полярной системы координат: . Выражение заменяется на .
Интеграл по той части фигуры, которая ближе к центру, как раз и будет взят с меньшим весом, а которая дальше от центра — с большим весом, ведь там больше. При замене , где , множитель фактически является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.
При переходе к полярным координатам, фрагмент круга фактически отображается в прямоугольную область. А это удобнее для вычисления, так как границы внутреннего и внешнего циклов становятся независимы друг от друга.
Пример. Вычислить интеграл где D — четверть круга единичного радиуса в первой четверти плоскости.
В декартовых координатах, этот интеграл имеет такой вид:
, что при вычислении внутреннего интеграла дало бы , в итоге привело бы к и потребовало бы ещё серию подстановок. В полярных координатах, решение гораздо более просто и удобно.
Луч находится в 1 четверти при . Радиус 1. Тогда:
= = = =
= = =
= = = .
Кстати, множители, не зависящие от , можно было сразу вынести во внешний интеграл, как видим, они всё равно умножаются на первообразную по и остаются неизменными, и выносятся во внешний интеграл по .
Пример. Доказать формулу площади круга с помощью полярных координат.
Решение. Так как надо вычислить площадь, то считаем .
= = = = = .
Похожие статьи:
poznayka.org
