Построение комплексного чертежа онлайн – 1.5 Алгоритм построения комплексного чертежа точки

1.5 Алгоритм построения комплексного чертежа точки

1. На оси абсцисс отложите координату Х и обозначьте А_Х.

2. Через А_Х проведите вертикальную линию связи, перпендикулярно оси Х. На этой линии связи отложите координату Y_A от оси Х (с учетом знака). Полученную горизонтальную проекцию точки обозначьте А₁.

3. На вертикальной линии связи отложите координату Z_A от оси Х (с учетом знака). Полученную фронтальную проекцию точки обозначьте А₂.

4. Из фронтальной проекции точки А₂ проведите горизонтальную линию связи, перпендикулярно оси Z. Пересечение линии связи с осью Z обозначьте А_Z.

5. Замерьте расстояние от оси X до горизонтальной проекции точки А₁ (координату Y_A).

6.Отложите измеренное расстояние (координату Y_A) на горизонтальной линии связи от оси Z (с учетом знака Y_A). Полученную профильную проекцию точки обозначьте А₃.

Если все координаты точки имеют числовые значения, то точка расположена в пространстве. Если точка имеет одну нулевую координату, то точка принадлежит плоскости проекций. Если точка имеет две нулевые координаты, то точка принадлежит оси проекций

1.6 Построение комплексного чертежа точки, принадлежащей пространству

Наглядное изображение

Комплексный чертеж

Пояснения

Дано: А(20,10,15)  1

Построить: комплексный чертеж

Y

1.По оси абсцисс от начала координат влево отложите Х =20.

2. Из А_x проведите вертикальную линию связи .

3. По линии связи, от оси Х вниз, отложите координату Y= 10 (вверх, если Y отриц.)

Обозначьте проекцию точки А_1.

4. От оси Х, по линии связи отложите вверх Z =15 (вниз, если Z отриц.). Обозначьте проекцию точки А_2.

Наглядное изображение

Комплексный чертеж

Пояснения

5.Из А₂ проведите горизонтальную линию связи.

6.Замерьте расстояние от оси Х до А

1 (показано фигурной скобкой).

7. Отложите это расстояние от оси Z по горизонтальной линии связи, вправо (если Y отриц., то влево).

8.Обозначьте проекцию точки А₃

1.7 Построение комплексного чертежа точки, принадлежащей плоскости проекций

Наглядное изображение

Комплексный чертеж

Пояснения

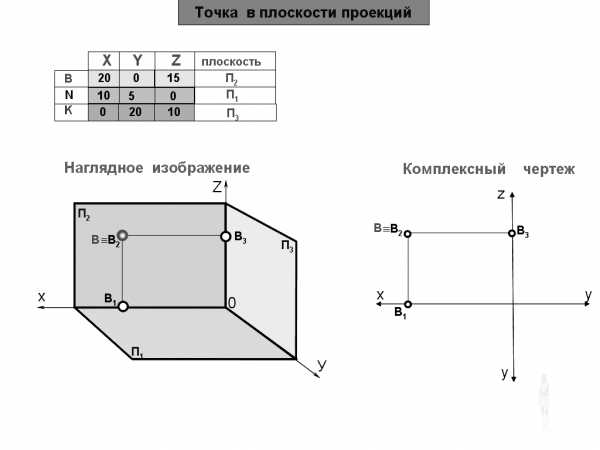
Дано: В(20,0,15)

Построить: комплексный чертеж

Так как координата Y=0, то точка В принадлежит фронтальной плоскости проекций.

0

Наглядное изображение

Комплексный чертеж

Пояснения

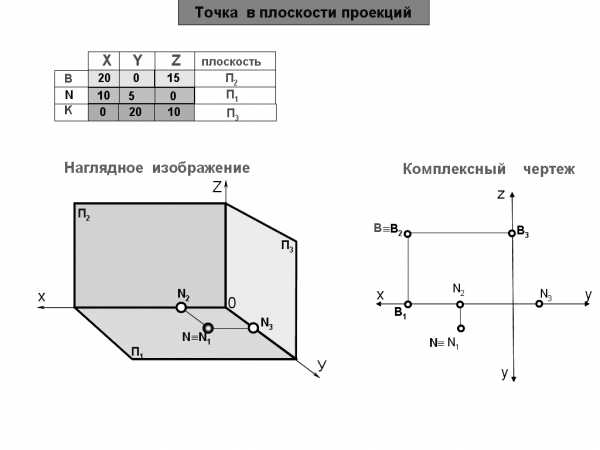
Дано: N (20,10,0)

Построить: комплексный чертеж

Так как координата Z=0, то точка N принадлежит горизонтальной плоскости проекций.

1.8 Построение комплексного чертежа точки, принадлежащей оси

Наглядное изображение

Комплексный чертеж

Пояснения

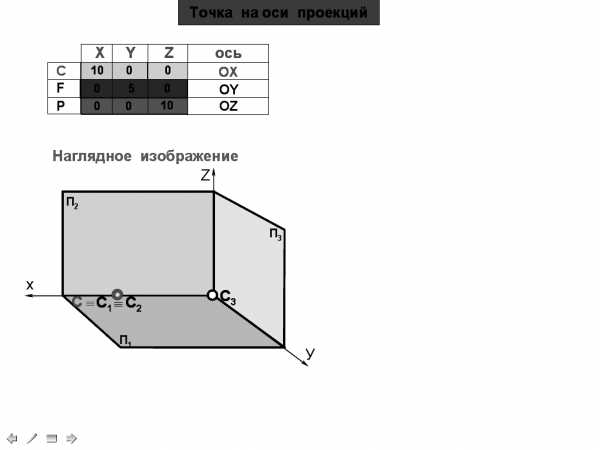
Дано: С (20,0,0)

Построить: комплексный чертеж.

Точка С принадлежит оси Х, т.к. две координаты имеют нулевые значения:

Y=0, Z=0.

0

Наглядное изображение

Комплексный чертеж

Пояснения

Дано: С (0,0,15)

Построить: комплексный чертеж.

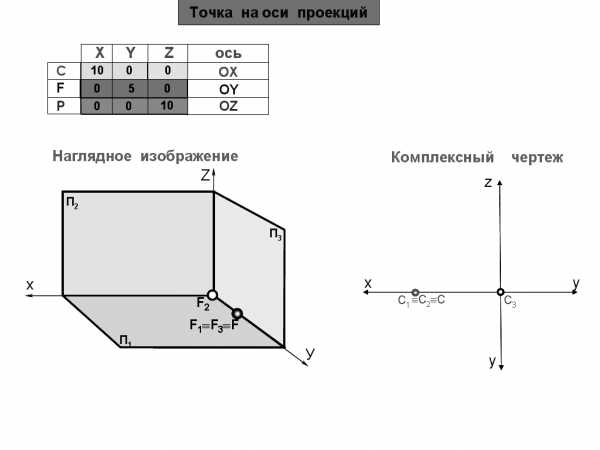
Точка P принадлежит оси Z, т.к. две координаты имеют нулевые значения:

X=0, Y=0.

Дано: F

(0,10,0)

Построить: комплексный чертеж.

Точка F принадлежит оси Y, т.к. две координаты имеют нулевые значения:

X=0, Z=0.

studfiles.net

4. Точка на комплексном чертеже.

1. Метод проекций.

Проекция (лат. projectio — выбрасывание вперёд) — изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости.

Термин проекция также означает метод построения такого изображения и технические приёмы, в основе которых лежит этот метод.

Принцип

Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S(центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Соединив эти точки прямыми линиями в том же порядке, как они соединены в предмете, получим на плоскости

перспективное изображение предмета или центральную проекцию.

Если центр проекции бесконечно удалён от картинной плоскости, то говорят о параллельной проекции, а если при этом проекционные лучи падают перпендикулярно к плоскости — то обортогональной проекции.

Проекция широко применяется в инженерной графике, архитектуре, живописи и картографии.

Изучением проекций и методов проектирования занимается начертательная геометрия.

Проекционный чертеж– чертеж, построенный методом проецирования пространственных объектов на плоскость. Является основным средством для анализа свойств пространственных фигур.

Аппарат проецирования:

• Центр проецирования (S)

• Проекционные лучи

• Объект проецирования

• Проекция

Комплексный чертеж– эпюр Монжа. Декартова система координат, ось (x,y,z)

Плоскости:

Фронтальная – вид спереди;

Горизонтальная – вид сверху;

Профильная – вид сбоку.

Состав комплексного чертежа:

1) Плоскости проекций

2) Оси проекций (пересечение плоскостей проекций)

3) Проекции

Линии связи.

2. Основные свойства ортогонального проецирования.

2 связанные между собой ортогональные проекции однозначно определяют положение точки относительно плоскостей проекции. 3-яя проекция не может быть задана произвольно.

Ортогональные проекции.

Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рис. 58). Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А’В’ = ABcosa.

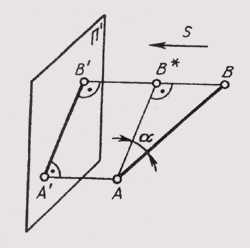
Рис. 58

При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.

Теорема о проецировании прямого угла. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.

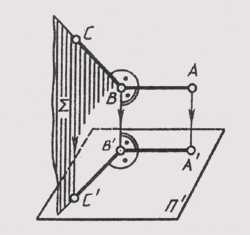
Рис. 59

Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости п’ (рис. 59). Проецирующая плоскость перпендикулярна плоскости п’. Значит, АВ _|_S, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В’С’. Но так какАВ || А’В’ _|_ В’С’, т. е. на плоскости п’ угол между А’В’ и В’С равен 90°.

Обратимость чертежа. Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (см. рис. 53) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п’. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А’. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).

3. Комплексный чертеж.

Прямая на комплексном чертеже:

Прямая общего положения– не параллельна и не перпендикулярна к плоскостям проекции.

Линии уровня– линии, параллельные плоскостям проекции:

• Горизонталь

• Фронталь

• Профильная

Общее свойство: у линий уровня одна проекция равна натуральной величине, другие проекции параллельны осям проекций.

Проецирующие прямые– дважды линии уровня (если перпендикулярны одной из плоскостей, то параллельны 2 другим):

• Горизонтально-проецирующая

• Фронтально-проецирующая

• Профильно-проецирующая

Конкурирующие точки– точки, лежащие на одной линии связи.

Взаимное расположение 2 прямых:

• Пересекающееся – имеют 1 общую точку и общие проекции этой точки

• Параллельные – проекции всегда параллельны у 2 параллельных прямых

• Скрещивающиеся – не имеют общих точек, пересекаются только проекции, а не сами прямые

• Конкурирующие – прямые лежат в плоскости перпендикулярной к одной из плоскостей проекций (н-р, горизонтально-конкурирующие)

Элементы трехпроекционного комплексного чертежа точки.

Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-

Рис. 62

ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.

Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.

Полученный комплексный чертеж точки называется трехпроек-ционным.

В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубинуfточки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.

Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.

Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-

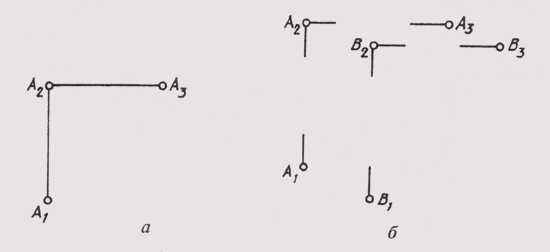
Рис. 63

ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).

5. Прямая на комплексном чертеже. Основные положения.

Комплексный чертеж прямой линии.

Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.

На рис. 69, а показаны прямая l и принадлежащие ей точки А и В. Для построения фронтальной проекции прямой l2 достаточно построить фронтальные проекции точек А2 и В2 и соединить их прямой. Аналогично строится горизонтальная проекция, проходящая через горизонтальные проекции точек А1 и В1. После совмещения плоскости П1 с плоскостью П2 получим двухпроекционный комплексный чертеж прямой l (рис. 69, б).

Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.

6. Определение натуральной величины отрезка прямой общего положения.

Определение натуральной величины отрезка прямой линии.

При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.

Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).

Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.

Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.

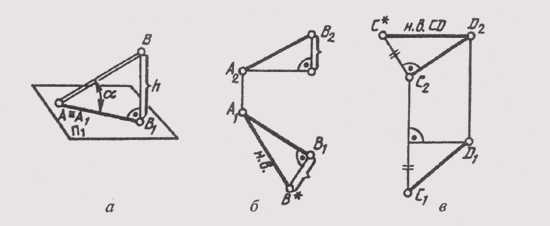
Рис. 78

Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см. § 36) или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка (см. §§58, 59).

треугольника.

Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.

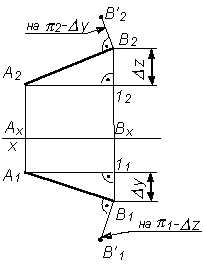
Вербальная форма	Графическая форма
1. Определить на комплексном чертеже Аz, Bz, Ay, By: D z – разность расстояний от точек А и В до плоскости p1; D y – разность расстояний от точек А и В до плоскости p2
2. Взять любую точку проекции прямой АВ, провести через нее перпендикуляр к отрезку: а) либо перпендикуляр к А2В2 через точку В2 или А2; б) либо перпендикуляр к А1В1 через точку В1 или А1
3. На этом перпендикуляре от точки В2 отложить D y или от точки B1 отложить D z
4. Соединить A2 и В’2; A1 и В’1
5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В’1 = А2В’2
6. Отметить углы наклона к плоскости проекции p1 и p2: a – угол наклона отрезка АВ к плоскости p1; б – угол наклона отрезка АВ к плоскости p2

При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на p 1, либо на p 2). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка.

studfiles.net

Построение комплексного чертежа точки — КиберПедия

Координаты точки принято писать в скобках рядом с обозначением точки. Например: запись В(3, 2, 3) означает, что координаты точки В следующие: Х=3; Y=2; Z=3. На рисунке 43 показаны построения на аксонометрическом изображении и на эпюре точки В по заданным координатам.

 

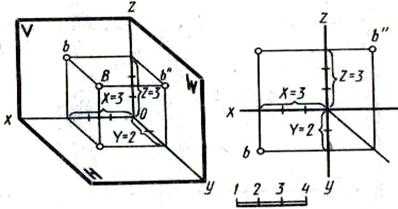
Рисунок 43 – Построение точки по заданным координатам

 

Материал для закрепления:

1. Указать условия, при которых можно определить положение точки в пространстве.

2. Указать, сколько проекций может иметь точка в пространстве на плоскости проекций.

3. Указать названия плоскостей проекций и их обозначения.

4. Указать каким образом располагаются плоскости проекций относительно друг друга.

5. Указать названия прямых линий, по которым пересекаются плоскости проекций.

6. Показать обозначение точки пересечения плоскостей проекций.

7. Показать обозначение точек проекций на плоскостях проекций.

8. Объяснить получение эпюра или комплексного чертежа.

9. Объяснить назначение эпюра.

10. Объяснить назначение координат точки.

11. Объяснить возможность переноса координат точки по оси Y.

12. Объяснить значение координат точки А (6, 10, 4).

 

После теоретического закрепления материала, обучающиеся выполняют индивидуальные практические задания на построение комплексного чертежа точки по заданным координатам, в соответствии с вариантом обучающегося

(задание 4а). Работа выполняется на формате А4 с соблюдением линий чертежа. Название чертежа – «Графическая работа №4. Проекции точки».

 

Построение комплексного чертежа прямой

Всякую линию, в том числе и прямую, можно рассматривать как множество последовательно расположенных точек в пространстве, а проекцию прямой АВ на плоскость Н – как множество проекций точек данной прямой (рисунок 44).

Рисунок 44 – Проекция прямой на плоскость

 

Положение прямой в пространстве определяют две её точки. Часть прямой, ограниченная двумя точками, называется отрезком. Чтобы построить проекции отрезка АВ, достаточно построить проекции его крайних точек. Соединив прямыми одноименные проекции этих точек, получим проекции отрезка (рисунок 45).

Рисунок 45 – Проекции отрезка

Положение отрезка прямой в пространстве определяется двумя его проекциями. Чтобы найти третью проекцию отрезка, необходимо построить третьи проекции точек, ограничивающих отрезок. На рисунке 45а,б стрелками показан ход построения профильной проекции а»б»отрезка АВ по заданным горизонтальной ав и фронтальной а’в’ проекциям.

 

Закрепление материала:

По заданным координатам точек отрезка АВ построить комплексный чертёж в соответствии со своим вариантом (задание 13, 14, 15). Работа выполняется на формате А4, с соблюдением линий чертежа и обозначение точек на плоскостях проекций (задание 4б).

Название чертежа – «Графическая работа №4. Проекции отрезка».

 

cyberpedia.su

Начертательная геометрия

3.1. Ортогональные (прямоугольные) проекции точки. Проецирование точки на три плоскости проекций

Рассмотрим систему трех взаимно перпендикулярных плоскостей проекций (рис. 5): П₁ горизонтальная плоскость проекций, П₂ фронтальная плоскость проекций и П₃ профильная плоскость проекций.

Рис. 5. Плоскости проекций:

x₁₂= П₁∩ П₂;

y₁₃= П₁∩ П₃;

z₂₃= П₂∩ П₃

Точка пересечения трех плоскостей O₁₂₃ – начало координат. Линия пересечения горизонтальной и фронтальной плоскостей называется осью проекций x₁₂= П₁∩ П₂ , линия пересечения горизонтальной и профильной плоскостей называется осью проекций y₁₃= П₁∩ П₃ , линия пересечения фронтальной и профильной плоскостей называется осью проекций z₂₃= П₂∩ П₃.

Поскольку плоскости проекций бесконечны, три плоскости разделят все пространство на восемь частей – октантов. Порядок отсчета октантов (см. рис. 5): слева от плоскости П₃ (против часовой стрелки) с первого по четвертый, справа – с пятого по восьмой .

Направление осей x,y,z в первом октанте считается положительным. Знаки осей, продолженных за начало координат, считают отрицательными.

Для получения проекций точки А на три плоскости (рис. 6) П₁ , П₂ и П₃ через точку А проводятся проецирующие лучи [AA₁) – до пересечения с плоскостью П₁ , [AA₂) – до пересечения с плоскостью П₂ и [AA₃) – до пересечения с плоскостью П₃. Точка A₁ – горизонтальная проекция точки , A₂ – фронтальная проекция точки , A₃ – профильная проекция точки . Точки A₁₂A₁₃A₂₃ – вспомогательные, лежащие соответственно на осях x,y,z .

Рис. 6. Проецирование точки на три плоскости проекций

Для получения плоского чертежа точки А необходимо повернуть плоскость П₁ вокруг оси x по часовой стрелке, а плоскость П₃ – вокруг оси z до совмещения с П₂ . Плоскость П₂ , точки A₂ и A₁₂ остаются неподвижными (рис. 7), точки A₁ и A₁₃ и ось y₁ поворачиваются вместе с П₁ . После поворота, точки A₁ , A₂ и A₁₂ образуют вертикальную линию связи. Точки A₃ и A₂₃ , поворачиваясь вместе с П₃ и осью y₃, образуют, после поворота, горизонтальную линию связи A₂ A₃ . Точки A₁ и A₃ соединяются ломаной линией связи A₁ A₀ A₃ . Вершина ломаной линии связи или точка преломления A₀ лежит на биссектрисе угла y₁O₁₂₃y₃ . Множество вершин ломаных линий связи определяют условную линию, называемую постоянной прямой комплексного чертежа k₁₂₃.

Рис. 7. Трехкартинный комплексный чертеж точки:

A₁A₁₃= O₁₂₃A₁₂= A₂A₂₃=x – широта А;

A₁A₁₂= O₁₂₃A₁₃= A₂₃A₃=y – глубина А;

A₂A₁₂= O₁₂₃A₂₃= A₃₁A₃=z – высота А;

Чертеж трех совмещенных плоскостей проекций называется трехкартинным комплексным чертежом. Метод образования комплексного чертежа называют методом Монжа, в честь французского ученого Гаспара Монжа, жившего в XIX веке, первым предложившего использовать совмещенные чертежи.

Для решения задач в начертательной геометрии часто используются чертежи на двух совмещенных плоскостях проекций, которые называются двухкартинными комплексными чертежами (рис. 8).

Рис. 8. Двухкартинный комплексный чертеж точек, занимающих различное положение относительно плоскостей проекций

cdot-nntu.ru

Программа для создания чертежей — AutoCAD, КОМПАС, NanoCAD, 3-D MAX

Строительство – это сначала проектирование, а потом – работа на объекте. Составление проекта в ХХI веке – это не бумажная, а компьютерная работа, и для этого разработано очень много специальных программ. Для объектов минимальной сложности может использоваться простая программа, для многоэтажных или многофункциональных сооружений существуют программы посложнее, но все они довольно быстро осваиваются даже начинающими проектировщиками. Это т.н. программы САПР для работы с чертежами (системы автоматизированного проектирования). Безусловными лидерами можно назвать программы для создания чертежей AutoCAD, Компас-3D, NanoCAD и 3-D Max из-за их доступности и многофункциональности. Что умеет каждая их этих программ, рассмотрим ниже:

Программный комплекс для ПК Autodesk AutoCAD

Простая программа для чертежей, но ее возможности можно увеличить за счет установки дополнительных модулей (плагинов). Работает в 2-D и 3-D измерении пространственных параметров, то есть, может создавать плоский рисунок или объемное изображение.AutoCAD

AutoCAD – программа для создания чертежей промышленной степени сложности. Софт может делать визуализацию схем и чертежей и проводить рендеринг объектов, который позволяет максимально приблизить зрительное восприятие макета к реальному.

Возможности САПР AutoCAD в 2-D и 3-D пространствах – это работа с объектами любой степени сложности. Вывод и сохранение файлов в форматах DWG, DWF и DXF позволяет получить полную совместимость с аналогичным софтом.

https://www.autodesk.ru/

Преимущества:

1. Программа – на русском языке;
2. Несколько десятков плагинов позволяют строить самые сложные объекты;
3. Проект можно сохранить в облаке MEGA, Coogle Disk, OneDrive, Яндекс Диск, Mail.Ru и т.д., распечатать на принтере или в 3-D;
4. Интеграция в разные форматы;
5. Устанавливается на все ОС на компьютере любого поколения, если он имеет подходящие технические характеристики (объем ОЗУ, параметры видеокарты, частота, разрядность).

Недостатки:

Программа платная.

Программа КОМПАС

Возможности программы для черчения широкие – она может работать со всеми форматами изображений. Наличие графического, визуального и текстового редактора. Программа для рисования может использоваться дома или в проектном бюро, с ее помощью легко реализуются и визуализируются строительные проекты. Обновление возможностей и исправление ошибок в программе происходит автоматически.САПР Компас

https://kompas.ru/kompas-3d-lt

Преимущества:

1. Простой софт для чертежей и схем позволяет освоить его даже начинающим чертежникам;
2. Объемная база типовых проектов и заготовок объектов, большое количество схем, чертежей, деталей, конструкций и проектов;
3. База плагинов и дополнительных инструментов для построения простых и сложных объектов;
4. Меню на русском языке;
5. Триал-версия для обучения персонала.

Недостатки:

Софт платный, а в триал-версии возможности ограничены.

NanoCAD

Программа намного проще, чем «AutoCAD» и «Компас», но для работы дома имеет обширный функционал, способный создавать качественные чертежи на ПК. Из-за простоты освоения программу часто используют, как обучающую. Вся графика соответствует САПР стандартам для 2-D проектирования, софт может проставлять размер и совместим с форматами DWG и DXF, что расширяет его возможности.NanoCAD

http://photoshop-archicad.com/nanocad/nanocad.html

Преимущества:

1. Платная версия стоит меньше, чем «AutoCAD» и «Компас»;
2. API позволяет внедрять свои приложения и сервисы;
3. Бесплатная версия, но с ограниченным функционалом.

Недостатки:

Не работает в 3-D, нет функции рендеринга.

При составлении простых чертежей, графиков или эскизов программа незаменима, но для разработки сложных объектов не годится, тем более, что трехмерную модель создать с ее помощью не получится. Хороший софт для обучения, персонального пользования и выполнения простейших домашних заготовок.

3-D MAX

Сама распространенная программа у всех чертежников. Наверное, все ее возможности не знают и сами разработчики. Сотни плагинов позволяют создавать объекты любой сложности и вложенности, визуализировать их в 3-D или 2-D пространстве, есть функция создания объемного панорамного видео, где объект можно вращать мышкой в любом направлении и в любой плоскости. 3-D MAX – программа бесплатная, но ее функционал значительно шире, чем у платных «AutoCAD», «NanoCAD» и «Компас» за счет бесплатных же плагинов и объемной базы заготовок моделей любой сложности и направленности.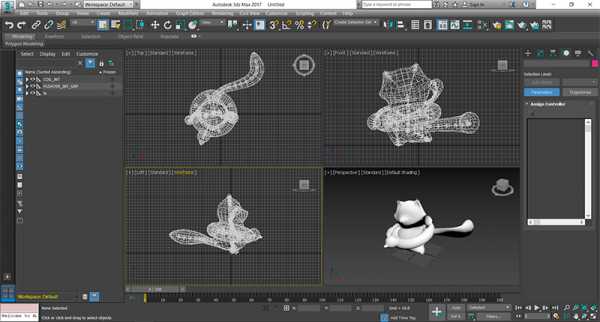Autodesk 3-D MAX

https://www.autodesk.ru/products/3ds-max/overview

Преимущества:

1. Autodesk 3-D MAX – программа бесплатная и бессрочная;
2. Как продолжение основной версии, разработаны облегченные версии 3-D MAX, при работе с которыми не «тормозят» и не «зависают» даже самые старые компьютеры;
3. В 3-D MAX предусмотрена возможность создания анимированных сцен, например, можно создавать те же компьютерные мультфильмы.

Недостатки:

Программа сложна в обучении, и даже небольшой перерыв в работе снижает уровень подготовки, так как софт постоянно обновляется и совершенствуется.

3-D Builder

Программа распространяется бесплатно, а в ОС Windows 10 она уже установлена по умолчанию, и освоить ее возможности можно довольно быстро даже без обучающих уроков. Интуитивно понятный интерфейс рассчитан на отсутствие навыков в работе с аналогичным софтом. Несложные чертежи, простые рисунки и эскизы – это то, что может предложить 3-D Builder.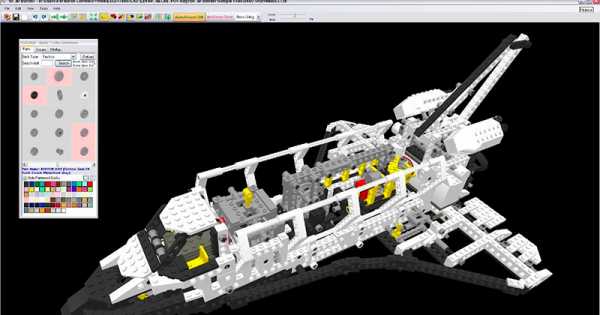3-D Builder

 

Преимущества:

1. Бесплатный доступ ко всему функционалу;
2. Работа с библиотеками готовых проектов и заготовок;
3. Взаимодействие с облачными хранилищами.

Недостатки:

На 3-D Builder невозможно разработать мало-мальский сложный проект, поэтому ее использование ограничивается домашней необходимостью.

Paint

Это самое распространенное ПО, базовая версия которого установлена в каждом компьютере, начиная с самых старых ОС. Тем не менее, рисовать простые чертежи, схемы, планы объектов и участков, делать рисунки или эскизы чертежей в ней можно, и обучиться работе в Paint можно за несколько минут. Заготовки, которые хранятся в библиотеке компьютера, значительно облегчают начало работы без навыков и базовых знаний.Paint

Предустановленный во всех версиях ОС Windows софт Paint имеет расширенные версии и дополнения для планшетов и даже смартфонов, позволяющие создавать рисунки стилосом или от руки.

 

VariCAD

Программа представляет собой мультиплатформенную систему автоматизированного создания проектов в 2D и 3D графике. VariCAD разрабатывался, как софт для проектирования в машиностроительной области, а также для черчения и расчетов механических узлов.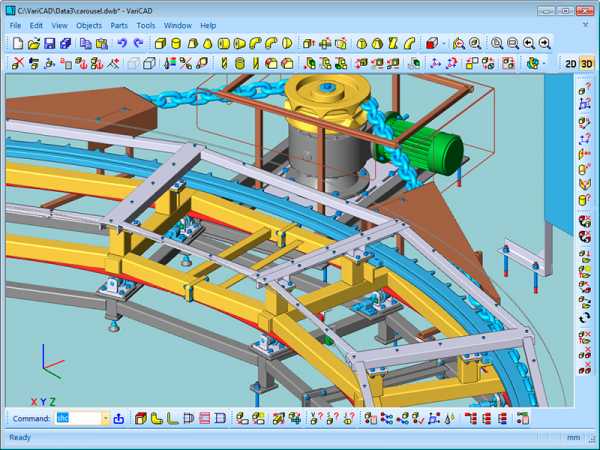VariCAD

https://soft.mydiv.net/win/download-VariCAD-for-Windows.html

Интерфейс VariCAD разработан с учетом простой и быстрой разработки двух- или трехмерных моделей. Внедрены средства разработки трубопроводов и емкостей различного уровня сложности. Предусмотрено одностороннее конвертирование 3D макетов в 2D графику без обратного преобразования.

Выбор того или иного софта зависит только от степени сложности проекта и необходимости выполнять простое задание на сложной программе.

jsnip.ru

ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.

ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.

ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.

Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д

Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.

Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П₁. Проекции элементов

пространства на ней будем обозначать с индексом 1 : А₁, а₁, S₁ … и называть горизонтальными проекциями (точки, прямой, плоскости).

Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П₂. Проекции элементов пространства на ней будем обозначать с индексом 2: А₂, <a₂, S₂ и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.

Спроецируем точку А ортогонально на обе плоскости проекций:

АА₁_|_ П₁;AА₁ ^П₁=A₁;

АА₂_|_ П₂;AА₂ ^П₂=A₂;

Проецирующие лучи АА₁ и АА₂ взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА₁АА₂, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.

Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П₁ с фронтальной плоскостью П₂ вращением вокруг оси П₂/П₁ (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П₂/П₁. Прямая А₁А₂, соединяющая горизонтальную А₁ и фронтальную А₂ проекции точки, называется вертикальной линией связи.

Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.

Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА₁ =h) и глубиной f(AA₂ =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А₂ чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.

Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П₁ и фронтальной плоскости проекций П₂ (рис. 62, а). В результате пересечения фронтальной П₂ и профильной П₃ плоскостей проекций получаем новую ось П₂/П₃, которая располагается на комплексном чертеже параллельно вертикальной линии связи A₁A₂ (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А₂ новой линией связи, которую называют горизонталь-

ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A₁A₂ _|_ А₂А₁ и А₂А₃, _|_ П₂/П₃.

Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П₃, которое обозначим буквой р.

Полученный комплексный чертеж точки называется трехпроек-ционным.

В трехпроекционном чертеже глубина точки АА₂ проецируется без искажений на плоскости П₁и П₂ (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А₁ и фронтальной А₂ проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A₂A₃ _|_A₂A₁. Затем в любом месте на чертеже провести ось проекций П₂/П₃ _|_ А₂А₃, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П₂/П₃. Получим профильную проекцию А₃ точки А.

Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.

Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-

ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).

Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:

Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П₁ [А₁ == В₁]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости

П₂ (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П₃ [А₃ == B₃] (рис. 64, в), они называются профильно конкурирующими.

По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.

Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.

На рис. 65, а показаны точка А и ее проекции — горизонтальная А₁ и фронтальная А₂. По условиям задачи необходимо произвести замену плоскостей П₂. Новую плоскость проекции обозначим П₄ и расположим перпендикулярно П₁. На пересечении плоскостей П₁ и П₄ получим новую ось П₁/П₄. Новая проекция точки А₄ будет расположена на линии связи, проходящей через точку А₁ и перпендикулярно оси П₁/П₄.

Поскольку новая плоскость П₄ заменяет фронтальную плоскость проекции П₂, высота точки А изображается одинаково в натуральную величину и на плоскости П₂, и на плоскости П₄.

Это обстоятельство позволяет определить положение проекции A₄, в системе плоскостей П₁ _|_ П₄ (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-

сти проекции П₂, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А₄ будет построена.

Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П₄ _|_ П₂ (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А₂А₄ _|_. В этом случае глубина точки одинакова и на плоскости П₁, и на плоскости П₄. На этом основании строят А₄ (рис. 66, б) на линии связи А₂А₄ на таком расстоянии от новой оси П₁/П₄ на каком А₁ находится от оси П₂/П₁.

Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П₅. Ее располагают перпендикулярно уже введенной плоскости П₄ (рис. 67, а), т. е. П₅П₄ и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П₁) и откладывают их на новой линии связи А₄А₅, от новой оси проекций П₅/П₄. В новой системе плоскостей П₄П₅ получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А₄ и А₅, связанных линией связи

Три основные плоскости проекций (П₁_|_П₂ _|_ П₃) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П₁/П₃ —осью координат у,П₂/П₃ —осью аппликат z.

Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).

Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А₁ ортогонально проецировать на ось х в точку А_х. Тогда получим пространственную координатную ломаную АА₁А_ХО, отрезки которой параллельны осям координат и соответственно называются: ОА_Х — отрезком абсциссы; А_Х А₁ — отрезком ординат; А₁А — отрезком аппликаты.

Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:

х = OA_X абсцисса; у = A_xA₁— ордината; z = AA₁ — аппликата.

Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение

вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.

Контакты для заказа чертежей

Справочная по строит. черч.

Телефон

89042493591

кроме выходных

задать вопрос, узнать о возможности, сроках и цене изготовления чертежей можно по аське:

587-149-933

Новости:

Открылся наш сайт

Здесь вы можете заказать красивые цветы из ткани на платье и заколки.

www.helpstudent5.narod.ru

Комплексный чертёж точки.

Наибольшее применение на практике получил чертёж, составленный из двух или более связанных между собой ортогональных проекций изображаемой фигуры. Такой чертёж называется комплексным чертежом в ортогональных проекциях или комплексным чертежом.

Принцип образования чертежа состоит в том, что данная фигура проецируется ортогонально на 2 взаимно ^-е плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.

Одна из плоскостей проекций располагается горизонтально, обозначается П₁ и называется горизонтальной плоскостью проекций.

2-я плоскость располагается вертикально перед наблюдателем, обозначается П₂ – фронтальная плоскость проекций. Прямая пересечения плоскостей – ось проекций.

А₁ – горизонтальная проекция А₂ – фронтальная проекция

h_А – высота точки А

f_А – глубина т.А

 

 

Спроецируем ортогонально на плоскости проекций П₁ и П₂ какую-нибудь

точку А, тогда получим две её проекции: горизонтальную проекцию А₁ на плос­кости П₁ и фронтальную проекцию А₂ на плоскости П₂. Проецирующие прямые AA₁ и АА₂, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость A₁AA₂, перпендикулярную к обеим плоскостям проекций и к оси проекций X. Прямые A_хA₁ и А_хА₂, являющиеся проекциями проецирующей плоскости на плоскостях проекций П₁ и П₂, будут перпендикулярны к оси проекций X.

Обратно, каждая пара точек А₁ и А₂, соответственно принадлежащих плос­костям П₁ и П₂ и расположенных на перпендикулярах к оси X, восставленных из одной и той же точки А_х, определяют в пространстве единственную точку А. В са­мом деле, если провести через точку A₁ и А₂ перпендикуляры А₁А и А₂А соответ­ственно к плоскостям П₁ и П₂, то они, находясь в одной плоскости А₁А_хА₂, пере­секутся в некоторой точке А. Расстояние A₁А точки А от горизонтальной плоскос­ти проекций называется высотой h точки А, ее расстояние А₂А от фронтальной плоскости проекций – глубиной f точки А.

Чтобы получить плоский чертеж, совместим плоскость проекций П₁ с плос­костью П₂, вращая переднюю полуплоскость П₁ вокруг оси Х вниз. В результате получим комплексный чертеж точки А (рис. 4), состоящий из двух проекций А₁ и А₂ точки А, лежащих на одной прямой, перпендикулярной к оси X. Прямая А₁А₂, соединяющая две проекции точки, называется вертикальной линией связи.

Полученный комплексный чертеж будет обратимым, т.е. по нему можно вос­становить оригинал. В самом деле, рассматривая, например, фронтальную проек­цию А₂ точки А и имея на чертеже ее глубину f=А_хА₁, можно построить точку А. Для этого надо восстановить перпендикуляр к плоскости чертежа в его точке А₂ и от плоскости чертежа отложить глубину искомой точки, тогда конец перпендику­ляра определит положение точки А.

На практике часто бывает безразличным положение изображаемой фигуры относительно неподвижной системы плоскостей проекций, поэтому при образова­нии комплексного чертежа можно отказаться от фиксации плоскостей проекций и оси проекций не изображать. Основанием этому может служить отмеченное шестое свойство параллельной проекции не изменять проекции фигуры при параллельном переносе плоскости проекций.

Плоскости проекций П₁ и П₂ разбивают все пространство на четыре части, называемые квадрантами или четвертями. При этом условимся нумеровать квад­ранты в порядке, указанном на рис., и называть их I, II, III и IV квадрантами.

Рис. 5 Двухкартинный комплексный чертёж

Если точка А лежит в I квадранте, то ее горизонтальная проекция A₁ будет принадлежать передней полуплоскости П₁, а фронтальная проекция А₂ — верхней полуплоскости П₂. При совмещении плоскостей проекций горизонтальная проек­ция A₁ точки А окажется расположенной ниже оси Х₁₂, а фронтальная проекция А₂ — выше оси Х₁₂ (рис. 5). В зависимости от положения точек в различных квад­рантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже (рис. 5), так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит точка.

Итак, комплексный чертеж, состоящий из двух ортогональных проекций (называемый еще двухкартинным чертежом), является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. В качестве такой плос­кости проекций применяется плоскость, перпендикулярная к обеим основным плоскостям П₁ и П₂, которая называется профильной плоскостью проекций. Ее обозначают П₃. Три плоскости проекций П₁, П₂ и П₃ образуют систему трех взаимно перпендикулярных плоскостей (рис. 6). Ребра полученного трехгранника будем обозначать через X, У, Z.

Рис. 6

П3 – профильная плоскость проекций А3 – профильная проекция т.А рА – широта т.А

трёхкартинный комплексный чертёж т.А

 

Рассмотрим построение трехкартинного комплексного чертежа. Пусть А — некоторая точка пространства. Опустим из точки А перпендикуляры на плоскости проекций П₁, П₂ и П₃: АА_i^П_i (i = 1, 2, 3). Основания этих перпендикуляров (точ­ки А₁, А₂, А₃) и являются соответственно горизонтальной, фронтальной и про­фильной проекциями точки А в системе плоскостей проекций П₁, П₂ и П₃. Заметим при этом, что проецирующие плоскости AA₁A₂, AA₁A₃ и АА₂А₃ перпендикулярны соответственно осям X, У, Z. Обозначив точки пересечения этих плоскостей с осями через А₁₂, А₁₃, А₂₃, заметим, что как прямые A₁A₁₂ и А₁₂А₂ перпендикулярны к оси X, так и две другие пары прямых A₁A₁₃, А₁₃А₃ и А₂А₂₃, А₂₃А₃ должны быть перпендикулярны соответственно осям Y и Z. Расстояние точки А от горизонтальной плоскости проекций П₁ мы назвали ранее высотой точки А, а расстояние точки А от фронтальной плоскости проекций П₂ — ее глубиной; расстояние точки А от профильной плоскости проекций П₃ будем называть широтой точки А.

При построении плоского чертежа плоскость П₂ считается неподвижной, а остальные плоскости П₁ и П₃ совмещаются с ней путем вращения соответственно вокруг осей Х и Z в направлении, указанном на рис. стрелками. После совме­щения плоскости П₁ с фронтальной плоскостью П₂ отрезки А₁А₁₂^Х₁₂ и A₁₂A₂^X₁₂ окажутся расположенными на одной прямой. Аналогично после со­вмещения плоскости П₃ с плоскостью П₂ отрезки A₂A₂₃^Z₂₃ и А₂₃А₃^Z₂₃ распо­ложатся на линии связи А₂А₃^Z₂₃.

В результате указанного совмещения плоскостей проекций получаем комп­лексный чертеж точки А, состоящий из трех ортогональных проекций (трехкартинный). При этом линии связи должны быть перпендикулярны к осям: А₁А₂^Х₁₂, А₂А₃^Z₂₃, а отрезки А₁А₁₂ и А₂₃А₃ равны, ибо А₁А₁₂ = А₂₃А₃ =А₂А есть глубина точки А.

Рассмотрим, какой линией связи можно соединять горизонтальную и про­фильную проекции точки А. Для этого обратим внимание на квадрат А₁₃ОА₃А*. Диагональ этого квадрата является биссектрисой угла Х₁₂ОZ₂₃. Следо­вательно, линия связи, соединяющая проекции А₁ и А₃, представляет собой лома­ную линию с вершиной на биссектрисе угла Х₁₂ОZ_23, состоящую из двух звеньев (горизонтального и вертикального). В дальнейшем эту линию будем называть горизонтально-вертикальной линией связи. Часть этой ломаной заменяют иногда дугой окружности.

Введенная система трех плоскостей проекций П₁, П₂ и П₃ разбивает все про­странство на восемь частей, называемых октантами. Их нумеруют следующим об­разом: слева от профильной плоскости октанты сохраняют нумерацию квадрантов, а справа от плоскости П₃ идут номера 5, 6, 7 и 8. При совмещении плоскостей про­екций передняя часть горизонтальной плоскости опускается вниз, а задняя подни­мается вверх; передняя часть профильной плоскости удаляется от нас направо, а задняя приближается слева.

Множество горизонтальных проекций всех точек пространства назовем по­лем горизонтальных проекций П₁ (соответствующая проекция фигуры называется видом сверху), а множество фронтальных проекций всех точек пространства — по­лем фронтальных проекций П₂ (соответствующая проекция фигуры называется ви­дом спереди или главным видом). Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П₃ (соответствующая проекция фигуры называется видом слева).

Чтобы иметь возможность точного построения комплексных чертежей каких-либо фигур, необходимо уметь задавать положения проекций точек, определяющих данные фигуры, при помощи чисел. Для этого, как известно, следует пользоваться координатным методом. Рассмотрим трехгранник, образованный системой плоскостей проекций П₁, П₂ и П₃. На осях X, У, Z установим единицу измерения е. За начало отсчета примем точку О пересечения трех плоскостей проекций (вершину трехгранника). Положительное направление на каждой оси установим, как показано на рис. Тогда трехгранник OXYZ можем рассматривать как прямоугольную декартову систему координат с коорди­натными осями: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат.

Ломаная ОА₁₂А₁А, определяющая положение точки А относительно коор­динатной системы OXYZ, называется, как, уже было сказано ранее, координатной ломаной линией. Звенья этой ломаной называются отрезками координат: ОА — отрезок абсциссы, А₁₂А₁ — отрезок ординаты, А₁А — отрезок аппликаты точки А. Длины отрезков координат точки А, измеренные установленной единицей длины е, называются координатами точки А:

Координаты точки А можно рассматривать, как ее расстояния до плос­костей проекций, поэтому координаты будут иметь следующие значения: Z_А — высота, Y_A — глубина, Х_A — широта точки А. Координаты точки называются определителем точки.

По заданным координатам точку А(Х_А,Y_A,Z_A) можно построить сле­дующим образом. Сначала с помощью единицы длины е строится отрезок OA₁₂, затем отрезок A₁₂A₁, параллельный оси Y, и, наконец, отрезок А₁А, параллельный оси Z. В результате получаем точку А.

5. Комплексный чертёж прямой линии

Пусть в I четверти расположен отрезок прямой l не параллельный и не перпендикулярный ни к одной из плоскостей проекций. Для построения его ортогональных проекций возьмём на прямой 2 точки и спроецируем их на П₁ и П₂. Полученные проекции точек и определяют искомые проекции отрезка прямой.

Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения.

К прямым частного положения относятся параллельные или ^-ые какой-либо плоскости проекций.

Прямая, //-ая какой-либо плоскости проекций, называется прямой уровня.

//-ая П₁ – горизонталь,

//-ая П₂ – фронталь,

//-ая П₃ – профильная прямая уровня.

Прямая уровня на плоскость проекций, которой она параллельна, проецируется без искажений в натуральную величину. При этом её проекция на этой плоскости с осями координат образует углы, равные углам наклона этой прямой к соответствующим плоскостям проекций.

Для задания профильной прямой уровня необходимо задавать на ней проекции двух точек.

Прямая, ^-я какой-либо плоскости проекций, называется проецирующей прямой.

^-я к П₁ – горизонтально проецирующая,

^-я к П₂ – фронтально проецирующая,

^-я к П₃ – профильно проецирующая.

2 точки, проекции которых на какую-либо плоскость проекций совпадают, называются конкурирующие точки.

Если совпадают горизонтальные проекции – горизонтально конкурирующие.

Из двух горизонтально конкурирующих точек на П₁ будет видна та, фронтальная проекция которой находится выше от оси х₁₂.

Из двух фронтально конкурирующих точек на П₂ будет видна та, горизонтальная проекция которой находится дальше от оси х₁₂.

6. Определение натуральной величины отрезка прямой

Натуральная величина отрезка прямой является гипотенузой прямоугольного треугольника одним катетом которого служит проекция отрезка на какую-либо плоскость проекций, а другим катетом разность расстояний концов этого отрезка до этой плоскости проекций.

 

Похожие статьи:

poznayka.org

No related posts.