Формула разложения на множители – Разложение многочлена на множители. Теория и примеры.

Разложение многочленов на множители

Разложение многочленов на множители – это тождественное преобразование, в результате которого многочлен преобразуется в произведение нескольких сомножителей – многочленов или одночленов.

Существует несколько способов разложения многочленов на множители.

Способ 1. Вынесение общего множителя за скобку.

Это преобразование основывается на распределительном законе умножения: ac + bc = c(a + b). Суть преобразования заключается в том, чтобы выделить в двух рассматриваемых компонентах общий множитель и «вынести» его за скобки.

Пример.

Разложим на множители многочлен 28х³ – 35х⁴.

Решение.

1. Находим у элементов 28х³ и 35х⁴ общий делитель. Для 28 и 35 это будет 7; для х³ и х⁴ – х³. Иными словами, наш общий множитель 7х³ .

2. Каждый из элементов представляем в виде произведения множителей, один из которых

7х³ : 28х³ – 35х⁴ = 7х³ ∙ 4 – 7х³ ∙ 5х.

3. Выносим за скобки общий множитель
7х³ : 28х³ – 35х⁴ = 7х³ ∙ 4 – 7х³ ∙ 5х = 7х³(4 – 5х).

Способ 2. Использование формул сокращенного умножения. «Мастерство» владением этим способом состоит в том, чтобы заметить в выражении одну из формул сокращенного умножения.

Пример.

Разложим на множители многочлен х⁶ – 1.

Решение.

1. К данному выражению мы можем применить формулу разности квадратов. Для этого представим х⁶ как (х³)², а 1 как 1², т.е. 1. Выражение примет вид:
(х³)² – 1 = (х³ + 1) ∙ (х³ – 1).

2. К полученному выражению мы можем применить формулу суммы и разности кубов:
(х³ + 1) ∙ (х

3 – 1) = (х + 1) ∙ (х² – х + 1) ∙ (х – 1) ∙ (х² + х + 1).

Итак,
х⁶ – 1 = (х³)² – 1 = (х³ + 1) ∙ (х³ – 1) = (х + 1) ∙ (х² – х + 1) ∙ (х – 1) ∙ (х² + х + 1).

Способ 3. Группировка. Способ группировки заключается в объединение компонентов многочлена таким образом, чтобы над ними было легко совершать действия (сложение, вычитание, вынесение общего множителя).

Пример.

Разложим на множители многочлен х³ – 3х² + 5х – 15.

Решение.

1. Сгруппируем компоненты таким образом: 1-ый со 2-ым, а 3-ий с 4-ым
(х³ – 3х²) + (5х – 15).

2. В получившемся выражении вынесем общие множители за скобки: х² в первом случае и 5 – во втором.
(х³ – 3х²) + (5х – 15) = х²(х – 3) + 5(х – 3).

3. Выносим за скобки общий множитель х – 3 и получаем:
х

2(х – 3) + 5(х – 3) = (х – 3)( х² + 5).

Итак,
х³ – 3х² + 5х – 15 = (х³ – 3х²) + (5х – 15) = х²(х – 3) + 5(х – 3) = (х – 3) ∙ ( х² + 5).

Закрепим материал.

Пример.

Разложить на множители многочлен a² – 7ab + 12b².

Решение.

1. Представим одночлен 7ab в виде суммы 3ab + 4ab. Выражение примет вид:
a² – (3ab + 4ab) + 12b².

Раскроем скобки и получим:
a² – 3ab – 4ab + 12b².

2. Сгруппируем компоненты многочлена таким образом: 1-ый со 2-ым и 3-ий с 4-ым. Получим:
(a² – 3ab) – (4ab – 12b²).

3. Вынесем за скобки общие множители:
(a² – 3ab) – (4ab – 12b²) = а(а – 3b) – 4b(а – 3b).

4. Вынесем за скобки общий множитель (а – 3b):
а(а – 3b) – 4b(а – 3b) = (а – 3 b) ∙ (а – 4b).

Итак,
a²

– 7ab + 12b² =
= a² – (3ab + 4ab) + 12b² =
= a² – 3ab – 4ab + 12b² =
= (a² – 3ab) – (4ab – 12b²) =
= а(а – 3b) – 4b(а – 3b) =
= (а – 3 b) ∙ (а – 4b).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Разложение многочленов на множители в комбинации с формулами сокращённого умножения

На предыдущих уроках мы изучили два способа разложения многочлена на множители – способ вынесения общего множителя и способ группировки. Кроме того, мы изучили формулы сокращенного умножения и говорили, что их также можно использовать для разложения многочлена на множители.

Теперь для начала рассмотрим простейшие способы комбинирования вышеуказанных методов разложения.

Пример 1:

;

Теперь усложним выражение, умножив заданный многочлен на три:

;

Данная формула очень похожа на полный квадрат, но в таком виде свернуть ее мы не можем, но мы видим, что у всех членов есть общий множитель и можем вынести его за скобку. Получаем:

;

Итак, первая комбинация это формулы сокращенного умножения плюс вынесение общего множителя за скобки.

Пример 2:

;

Определим, что можно вынести за скобки. Для этого для начала найдем НОД:

;

Вынесем найденный общий множитель:

;

Определим, какие буквенные множители можно вынести. Обе переменные a и b есть во всех членах многочлена, значит, их можно выносить. Осталось определить только, в какой степени. Для этого найдем минимальную степень каждой из переменных. Это  и . Вынесем найденную буквенную часть:

;

Распишем полученную скобку более подробно, для этого определим, квадратами каких выражений являются первое и третье выражение, а затем проверим удвоенное произведение:

;

Очевидно, что в скобке стоит полный квадрат разности, так как мы помним его формулу: . Свернем его:

;

Пример 3:

;

Сгруппируем первый, третий и четвертый член, получим:

;

В скобках мы видим квадрат суммы. Свернем его:

;

Теперь мы видим разность квадратов. Вспомним формулу: . На основании этой формулы распишем наше выражение:

;

Итак, мы рассмотрели комбинацию способа группировки и формул сокращенного умножения.

Пример 4:

Поступаем аналогично предыдущему примеру: сначала группируем члены по схеме «3+1», после этого применяем формулы сокращенного умножения:

;

Пример 5:

Очевидно, что нужно вынести  за скобки:

В скобках мы получили формулу суммы кубов. Распишем ее:

В данном примере мы применили комбинацию вынесения общего множителя за скобки и формулы куба суммы.

Пример 6:

;

Распишем разность квадратов:

;

Пример 7:

;

Вынесем общий множитель за скобки:

;

Во второй скобке мы видим квадрат разности, можем свернуть его:

;

Вывод: в данном уроке мы рассмотрели простейшие комбинации способов разложения многочлена на множители и формул сокращенного умножения и решили много различных примеров на разные варианты этих комбинаций.

 

Список рекомендованной литературы

1) Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2) Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3) Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет:

1. Школьный помощник (Источник).

2. Математика для чайников (Источник).

3. ЕГЭ по математике (Источник).

 

Рекомендованное домашнее задание:

Задание 1: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 890, ст.224;

Задание 2: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 897, ст.225

Задание 3: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, №899, ст. 225;

interneturok.ru

Разложение многочлена на множители. Часть 2

Разложение многочлена на множители. Часть 2

В этой статье мы продолжим разговор о том, как раскладывать многочлен на множители. Мы уже говорили о том, что разложение на множители — это универсальный прием, помогающий решить сложные уравнения и неравенства. Первая мысль, которая должна прийти в голову при решении уравнений и неравенств, в которых в правой части стоит ноль — попробовать  разложить левую часть на множители.

Перечислим основные  способы разложения многочлена на множители:

• вынесение общего множителя за скобку
• использование формул сокращенного умножения
• по формуле разложения на множители квадратного трехчлена
• способ группировки
• деление многочлена на двучлен
• метод неопределенных коэффициентов.

Мы уже подробно рассмотрели первые три способа разложения на множители. В этой статье мы остановимся на четвертом способе, способе группировки.

Если количество слагаемых в многочлене превышает три, то мы пытаемся применить способ группировки. Он заключается в следующем:

1.Группируем слагаемые определенным образом так, чтобы потом каждую группу можно было разложить на множители каким-то способом. Критерий того, что слагаемые сгруппированы верно — наличие одинаковых множителей в каждой группе. 

2. Выносим за скобку одинаковые множители.

Поскольку этот способ применяется наиболее часто, разберем его на примерах.

Пример 1. Разложить на множители выражение:

Решение. 1. Объединим слагаемые в группы:

2. Вынесем из каждой группы общий множитель:

3. Вынесем множитель, общий для обеих групп:

Итак, 

Пример 2. Разложить на множители выражение: 

1. Сгруппируем последние три слагаемых и разложим на множители по формуле квадрата разности:

2. Разложим получившееся  выражение на множители по формуле разности квадратов:

Итак,

 

Пример 3. Решить уравнение: 

В левой части уравнения четыре слагаемых. Попробуем разложить левую часть на множители с помощью группировки.

1. Чтобы структура левой части уравнения была яснее, введем замену переменной: , 

Получим уравнение такого вида:

2. Разложим левую часть на множители с помощью группировки:

Внимание! Чтобы не ошибиться со знаками, я рекомендую объединять слагаемые в группы «как есть», то есть не меняя знаки коэффициентов, и следующим действием, если необходимо, выносить за скобку «минус».

3. Итак, мы получили  уравнение:

Отсюда .

То есть 

4. Вернемся к исходной переменной:

Разделим обе части на . Получим: . Отсюда 

Ответ: 0

Пример 4. Решить уравнение:

Чтобы структура уравнения стала более «прозрачной», введем замену переменной:

, 

Получим уравнение:

Разложим левую часть уравнения на множители. Для этого сгруппируем первое и второе слагаемые и вынесем за скобку :

,

вынесем за скобку :

.

Вернемся к уравнению:

Отсюда или ,

или

Вернемся к исходной переменной:

или

Чтобы решить эти уравнения, нужно вспомнить, как решаются простейшие тригонометрические уравнения.

Получаем:

,  ;

, 

или

,  ;

,  ;

Ответ: ,  ,  , 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

7 класс. Алгебра. Разложение многочленов на множители с помощью формул сокращенного умножения. — Разложение многочленов на множители с помощью формул сокращенного умножения.

Комментарии преподавателя

На данном уроке мы научимся раскладывать многочлен на множители с применением всех ранее изученных методов. Мы научимся решать задачи с различными комбинациями формул сокращенного умножения и методов разложения.

 

 

Тема: Раз­ло­же­ние мно­го­чле­нов на мно­жи­те­ли

Урок: Раз­ло­же­ние мно­го­чле­нов на мно­жи­те­ли в ком­би­на­ции с фор­му­ла­ми со­кра­щен­но­го умно­же­ния

На преды­ду­щих уро­ках мы изу­чи­ли два спо­со­ба раз­ло­же­ния мно­го­чле­на на мно­жи­те­ли – спо­соб вы­не­се­ния об­ще­го мно­жи­те­ля и спо­соб груп­пи­ров­ки. Кроме того, мы изу­чи­ли фор­му­лы со­кра­щен­но­го умно­же­ния и го­во­ри­ли, что их также можно ис­поль­зо­вать для раз­ло­же­ния мно­го­чле­на на мно­жи­те­ли.

Те­перь для на­ча­ла рас­смот­рим про­стей­шие спо­со­бы ком­би­ни­ро­ва­ния вы­ше­ука­зан­ных ме­то­дов раз­ло­же­ния.

При­мер 1:

;

Те­перь услож­ним вы­ра­же­ние, умно­жив за­дан­ный мно­го­член на три:

;

Дан­ная фор­му­ла очень по­хо­жа на пол­ный квад­рат, но в таком виде свер­нуть ее мы не можем, но мы видим, что у всех чле­нов есть общий мно­жи­тель и можем вы­не­сти его за скоб­ку. По­лу­ча­ем:

;

Итак, пер­вая ком­би­на­ция это фор­му­лы со­кра­щен­но­го умно­же­ния плюс вы­не­се­ние об­ще­го мно­жи­те­ля за скоб­ки.

При­мер 2:

;

Опре­де­лим, что можно вы­не­сти за скоб­ки. Для этого для на­ча­ла най­дем НОД:

;

Вы­не­сем най­ден­ный общий мно­жи­тель:

;

Опре­де­лим, какие бук­вен­ные мно­жи­те­ли можно вы­не­сти. Обе пе­ре­мен­ные a и b есть во всех чле­нах мно­го­чле­на, зна­чит, их можно вы­но­сить. Оста­лось опре­де­лить толь­ко, в какой сте­пе­ни. Для этого най­дем ми­ни­маль­ную сте­пень каж­дой из пе­ре­мен­ных. Это  и . Вы­не­сем най­ден­ную бук­вен­ную часть:

;

Рас­пи­шем по­лу­чен­

www.kursoteka.ru

примеры и формулы :: SYL.ru

Разложение квадратных трехчленов на множители относится к школьным заданиям, с которыми рано или поздно сталкивается каждый. Как его выполнить? Какова формула разложения квадратного трехчлена на множители? Разберемся пошагово с помощью примеров.

Общая формула

Разложение квадратных трехчленов на множители осуществляется решением квадратного уравнения. Это несложная задача, которую можно решить несколькими методами — нахождением дискриминанта, при помощи теоремы Виета, существует и графический способ решения. Первые два способа изучаются в средней школе.

Общая формула выглядит так: lx²+kx+n=l(x-x₁)(x-x₂) (1)

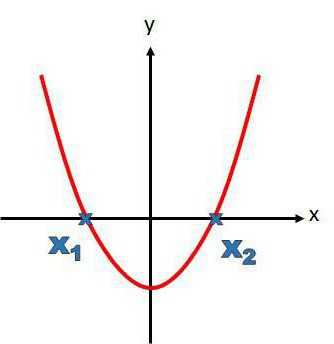
Алгоритм выполнения задания

Для того чтобы выполнить разложение квадратных трехчленов на множители, нужно знать теорему Вита, иметь под рукой программу для решения, уметь находить решение графически или искать корни уравнения второй степени через формулу дискриминанта. Если дан квадратный трехчлен и его надо разложить на множители, алгоритм действий такой:

1) Приравнять исходное выражение к нулю, чтобы получить уравнение.

2) Привести подобные слагаемые (если есть такая необходимость).

3) Найти корни любым известным способом. Графический метод лучше применять в случае, если заранее известно, что корни — целые и небольшие числа. Нужно помнить, что количество корней равно максимальной степени уравнения, то есть у квадратного уравнения корней два.

4) Подставить значение х в выражение (1).

5) Записать разложение квадратных трехчленов на множители.

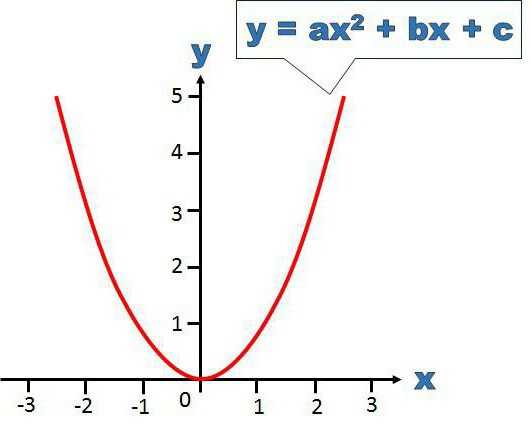
Примеры

Окончательно понять, как выполняется это задание, позволяет практика. Иллюстрируют разложение на множители квадратного трехчлена примеры:

необходимо разложить выражение:

х²-17х=-32

Прибегнем к нашему алгоритму:

1) х²-17х+32=0

2) подобные слагаемые сведены

3) по формуле Виета найти корни для этого примера сложно, потому лучше воспользоваться выражением для дискриминанта:

D=289-128=161=(12,69)²

x₁=2,155

x₂=14,845

4) Подставим найденные нами корни в основную формулу для разложения:

(х-2,155)_*(х-14,845)

5) Тогда ответ будет таким:

х²-17х+32=(х-2,155)(х-14,845)

Проверим, соответствуют ли найденные дискриминантом решения формулам Виета:

2,155+14,845=17

14,845^.2,155=32

Для данных корней применяется теорема Виета, они были найдены правильно, а значит полученное нами разложение на множители тоже правильно.

Аналогично разложим 12х²+7х-6.

12х²+7х-6=0

D=337

x₁=-7+(337)^1/2

x₂=-7-(337)^1/2

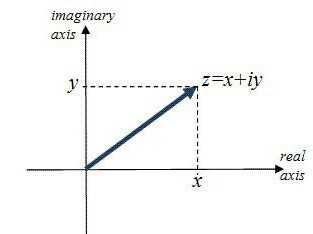
В предыдущем случае решения были нецелыми, но действительными числами, найти которые легко, имея перед собой калькулятор. Теперь рассмотрим более сложный пример, в котором корни будут комплексными: разложить на множители х²+4х+9. По формуле Виета корни найти не получится, и дискриминант отрицательный. Корни будут на комплексной плоскости.

D=-20

Исходя из этого, получаем нтересующие нас корни -4+2i*5^1/2 и -4-2i_*5^1/2 , поскольку (-20)^1/2=2i*5^1/2.

Получаем искомое разложение, подставив корни в общую формулу.

Еще один пример: нужно разложить на множители выражение 23х²-14х+7.

Имеем уравнение 23х²-14х+7=0

D=-448

Значит, корни 14+21,166i и 14-21,166i. Ответ будет такой:

23х²-14х+7=23(х-14-21,166i )*(х-14+21,166i ).

Приведем пример, решить который можно без помощи дискриминанта.

Пусть нужно разложить квадратное уравнение х²-32х+255. Очевидно, его можно решить и дискриминантом, однако быстрее в данном случае подобрать корни.

x₁=15

x₂=17

Значит х²-32х+255=(х-15)(х-17).

www.syl.ru