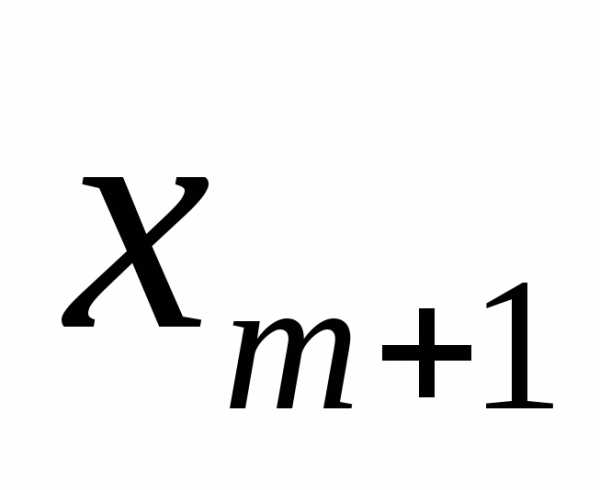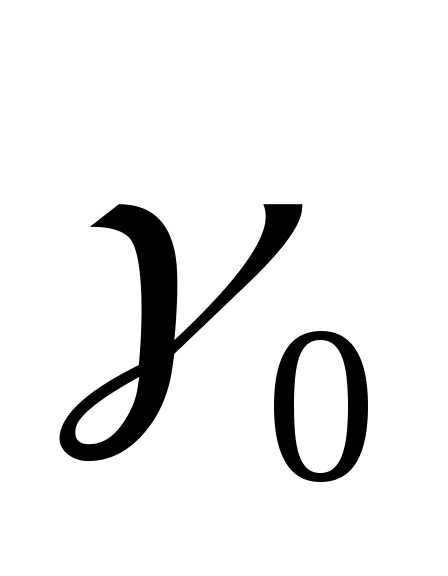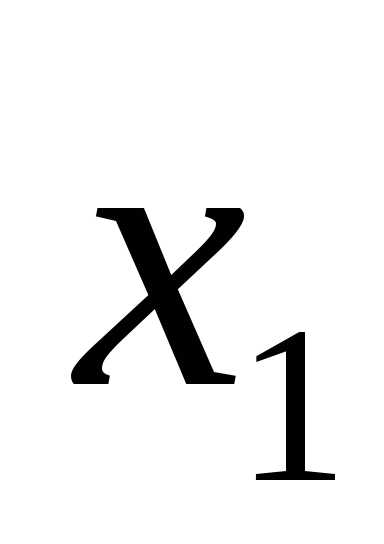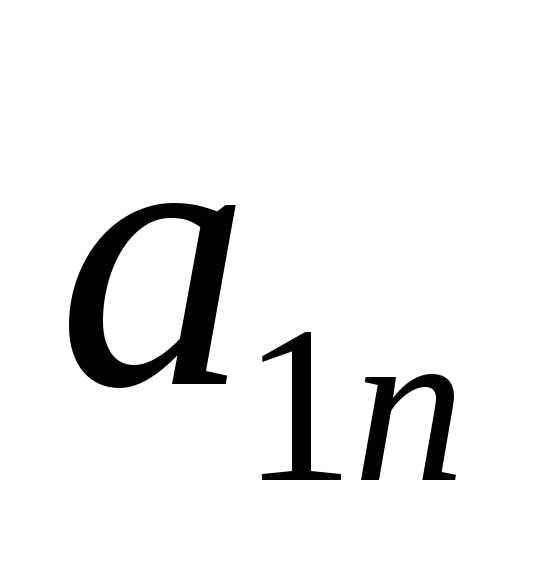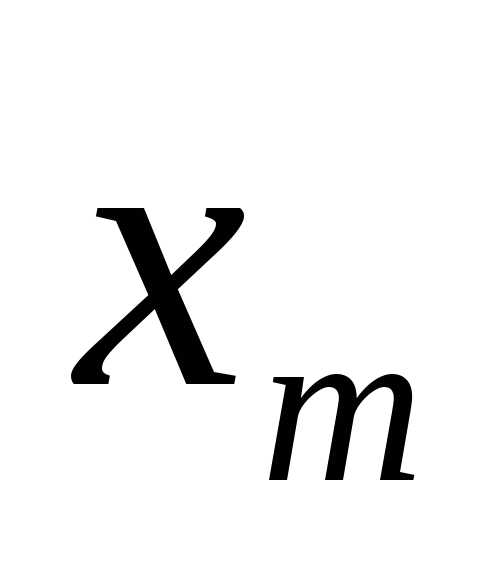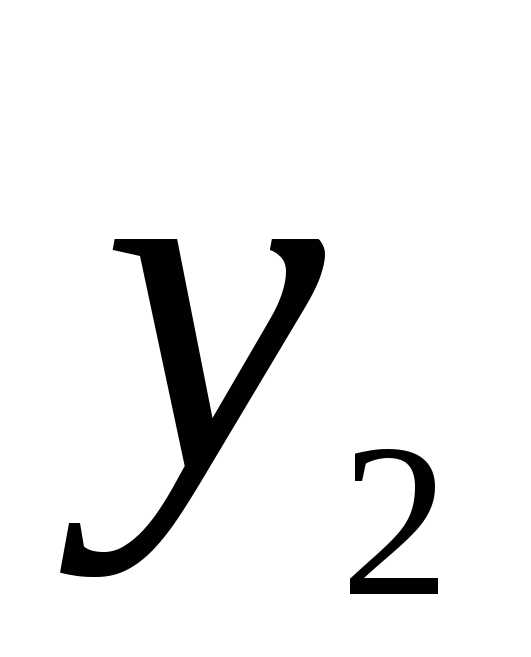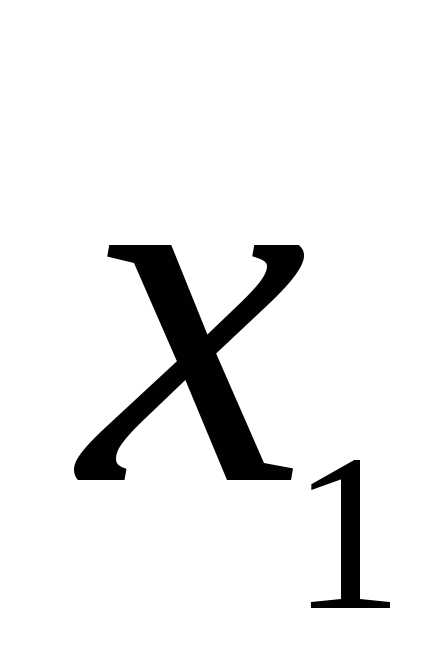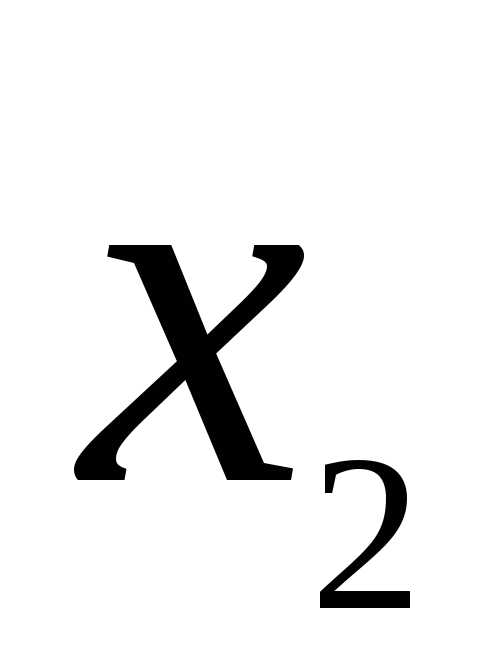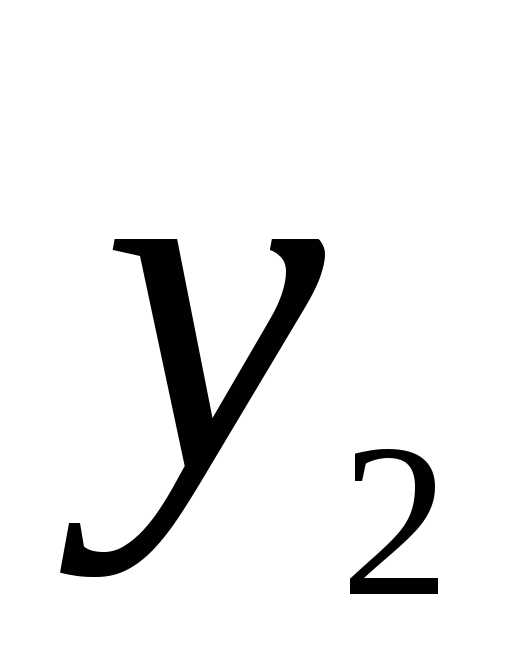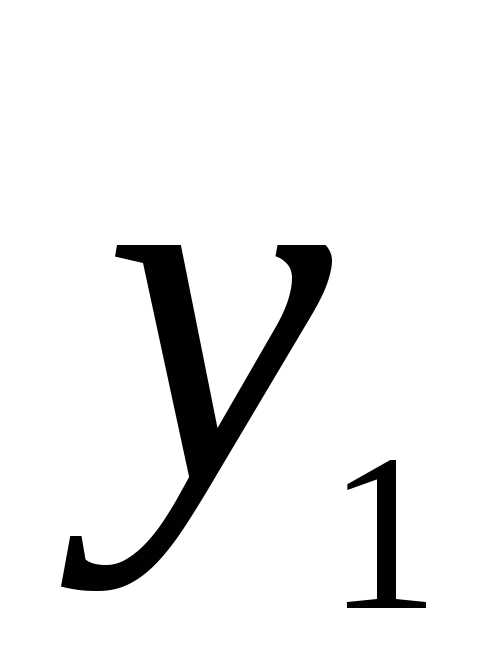Пример — Табличный симплекс метод
Необходимо решить задачу линейного программирования.
Целевая функция:
2x 1+5x2+3x3+8x4 →min
Ограничивающие условия:
3x1+6x2-4x3+x4≤12
4x1-13x2+10x3+5x4≥6
3x1+7x2+x3≥1
Приведем систему ограничений к каноническому виду, для этого необходимо перейти от неравенств к равенствам, с добавлением дополнительных переменных.
Так как наша задача — задача минимизации, то нам необходимо преобразовать ее к задаче на поиск максимума. Для этого изменим знаки коэффициентов целевой функции на противоположные. Элементы первого неравенства записываем без изменений, добавив в него дополнительную переменную x5 и изменив знак «≤» на «=». Т. к. второе и третье неравенства имеют знаки «≥» необходимо поменять знаки их коэффициентов на противоположные и внести в них дополнительные переменные x
3x1+6x2-4x3+x4+x5=12
-4x1+13x2-10x3-5x4+x6=-6
-3x1-7x2-x3+x7=-1
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции с противоположным знаком.
x1 | x2 | x3 | x4 | Своб член | |
| F | 2 | 5 | 3 | 8 | |
| X5 | 3 | 6 | -4 | 1 | 12 |
| X6 | -4 | 13 | -10 | -5 | -6 |
| X7 | -3 | -7 | -1 | -1 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю — это элемент: -6, он задает ведущую строку — X6. В этой строке так же находим максимальный по модулю отрицательный элемент: -10 он находится в столбце X3 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X2 | X6 | X4 | Своб член | |
| F | 0.8 | 8.9 | 0.3 | 6.5 | -1.8 |
| X5 | 4.6 | 0.8 | -0.4 | 3 | 14.4 |
| X3 | 0.4 | -1.3 | -0.1 | 0.5 | 0.6 |
| X7 | -2.6 | -8.3 | -0.1 | 0.5 | -0.4 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю — это элемент: -0.4, он задает ведущую строку — X7. В этой строке так же находим максимальный по модулю отрицательный элемент: -8.3 он находится в столбце X2 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X7 | X6 | X4 | Своб член | |
| F | -1.988 | 1.072 | 0.193 | 7.036 | -2.229 |
| X5 | 4.349 | 0.096 | -0.41 | 3.048 | 14.361 |
| X3 | 0.807 | -0.157 | -0.084 | 0.422 | 0.663 |
| X2 | 0.313 | -0.12 | 0.012 | -0.06 | 0.048 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент — это -1.988 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X2, а ведущий элемент: 0.313.
| X2 | X7 | X6 | X4 | Своб член | |
| F | 6.351 | 0.31 | 0.269 | 6.655 | -1.924 |
| X5 | -13.895 | -0.577 | 3.882 | 13.694 | |
| X3 | -2.578 | 0.152 | -0.115 | 0.577 | 0.539 |
| X1 | 3.195 | -0.383 | 0.038 | -0.192 | 0.153 |
Так как в строке F нет отрицательных элементов, то
найдено оптимальное решение. Так как исходной задачей был поиск минимума, то оптимальным решением будет свободный член строки F, взятый с противоположным знаком. F=1.924
при значениях переменных равных: x3=0.539, x1=0.153. Переменные x2 и x4 не входят в базис, поэтому x2=0 x4=0.
uchimatchast.ru
Симплекс метод пример отсутствия решения
Условие задачи
Математическая модель задачи:F = 4·x1 + 5·x2 + 4·x3 –>max
Решаем симплекс методом.
Вводим дополнительные переменные x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, чтобы неравенства преобразовать в равенства.
В качестве базиса возьмем x4 = 240; x5 = 200; x6 = 160.
Данные заносим в симплекс таблицу
Симплекс таблица № 1
Целевая функция:
0 · 240 + 0 · 200 + 0 · 160 = 0
Вычисляем оценки по формуле:
Δ1 = 0 · 2 + 0 · 4 + 0 · 4 – 4 = – 4
Δ2 = 0 · 3 + 0 · 2 + 0 · 6 – 5 = – 5
Δ3 = 0 · (–6) + 0 · (–4) + 0 · (–8) – 4 = – 4
Δ4 = 0 · 1 + 0 · 0 + 0 · 0 – 0 = 0
Δ5 = 0 · 0 + 0 · 1 + 0 · 0 – 0 = 0
Δ6 = 0 · 0 + 0 · 0 + 0 · 1 – 0 = 0
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ2 = – 5
Вводим переменную x2 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x2.
= 26.667
Наименьшее неотрицательное: Q3 = 26.667. Выводим переменную x6 из базиса
3-ю строку делим на 6.
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2
Вычисляем:
Получаем новую таблицу:
Симплекс таблица № 2
Целевая функция:
0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 0 · 8/3 + 5 · 2/3 – 4 = – 2/3
Δ2 = 0 · 0 + 0 · 0 + 5 · 1 – 5 = 0
Δ3 = 0 · (–2) + 0 · (–4)/3 + 5 · (–4)/3 – 4 = – 32/3
Δ4 = 0 · 1 + 0 · 0 + 5 · 0 – 0 = 0
Δ5 = 0 · 0 + 0 · 1 + 5 · 0 – 0 = 0
Δ6 = 0 · (–1)/2 + 0 · (–1)/3 + 5 · 1/6 – 0 = 5/6
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ3 = – 32/3
Вводим переменную x3 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x3.
< 0
< 0
< 0
Поскольку среди оценок нет неотрицательных, то решения не существует. Целевая функция может быть сделана сколь угодно большой.
Ответ: Решения задачи не существует. Целевая функция может быть сколь угодно большой.Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Пример решения задачи математического программирования симплекс-методом.
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
Z = -X1 + 8X2 max(min)
X1 – 2X2 ≤ -2,
-2X1 + 3X2 ≤ 6
2X1 + 4X2 ≤ 0,
X2≥0
Решение
Вместо переменной Х1 произвольного знака вводим переменные Х1’ и X1’’.
X1 = Х1’ — X1’’.
Запишем систему неравенств в виде:
(Х1’ — X1’’) — 2Х2 ≤ -2
-2(Х1’ — X1’’) + 3Х2 ≤ 6
2(Х1’ — X1’’) + 4Х2 ≤ 0
Получим:
Х1’ — X1’’- 2Х2 ≤ -2
-2Х1’ + 2X1’’+ 3Х2 ≤ 6 (1)
2Х1’ — 2X1’’ +4Х2 ≤ 0
Условие положительности:
Х1’≥0, X1’’≥0, X2≥0. (2)
Целевая функция:
F = -(Х1’ — X1’’) + 8X2 = -Х1’ + X1’’ + 8X2 (max) (3)
Задача записана в симметричной фоме записи. Приведем задачу к канонической форме записи, для этого введем дополнительные переменные Х3, Х4, Х5. Расширенная система задачи имеет вид:
Х1’ — X1’’- 2Х2 +Х3 = -2
-2Х1’ + 2X1’’+ 3Х2 +Х4 = 6
2Х1’ — 2X1’’ + 4Х2 +Х5 = 0
Условия неотрицательности примут вид:
Xj≥0 (j=1,..,5).
Заполним первую симплексную таблицу (Табл. 1), в которой переменные X3, X4, X5 являются базисными, переменные Х1’, X1’’, X2 свободными. Последняя строка заполняется коэффициентами целевой функции с противоположным знаком.
Таблица 1. Первая (начальная) симплексная таблица
|
Базис |
C |
Свободный член |
Переменные |
Оценочное отношение |
|||||
|
X1′ |
X1» |
X2 |
X3 |
X4 |
X5 |
||||
|
-1 |
1 |
8 |
0 |
0 |
0 |
||||
|
X3= |
0 |
-2 |
1 |
-1 |
-2 |
1 |
0 |
|
1 |
|
X4= |
0 |
6 |
-2 |
2 |
3 |
0 |
1 |
0 |
2 |
|
X5= |
0 |
0 |
2 |
-2 |
4 |
0 |
0 |
1 |
0 |
|
F |
0 |
1 |
-1 |
-8 |
0 |
0 |
0 |
|
|
В результате симплексного преобразования, получим вторую симплексную таблицу (Табл.2).
Таблица 2. Вторая симплексная таблица
|
Базис |
C |
Свободный член |
Переменные |
Оценочное отношение |
|||||
|
X1′ |
X1» |
X5 |
X3 |
X4 |
X5 |
||||
|
-1 |
1 |
8 |
0 |
0 |
0 |
||||
|
X3= |
0 |
-2 |
2 |
-2 |
0 |
1 |
0 |
0,5 |
1 |
|
X4= |
0 |
6 |
-3,5 |
3,5 |
0 |
0 |
1 |
-0,75 |
1,7142857 |
easyhelp.su
2.7. Двойственный симплекс-метод
Метод работает с теми же симплексными таблицами, что и прямой симплекс-метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис [1,3].
Вычислительная схема двойственного симплекс-метода
Шаг 0. Начинаем с симплексной таблицы, где .
B | | … | | |
L | | | … | |
| | | … | |
… | … | ………….. | ||
| | … | | |
Шаг 1. Проверка на оптимальность. Если , то решение– оптимальное.
Шаг
2. Выбор
ведущей строки. Выбираем среди номеров i,
для которых 
,
номерk с максимальным по модулю значением
.
Строка k объявляется ведущей.
Шаг 3. Проверка на неразрешимость. Если в строке нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.
Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки элемент с номеромs, для которого выполняется равенство
.
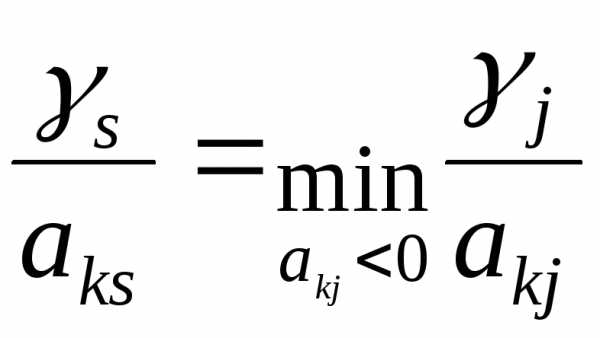Столбец s объявляется ведущим, а элемент 
– ведущим элементом.
Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).
2.8.Пример решения задачи двойственным симплекс-методом Решить задачу лп двойственным симплекс-методом:
Приводим задачу к каноническому виду:
Знаки
в ограничениях заменили противоположными
для того, чтобы переменные 
и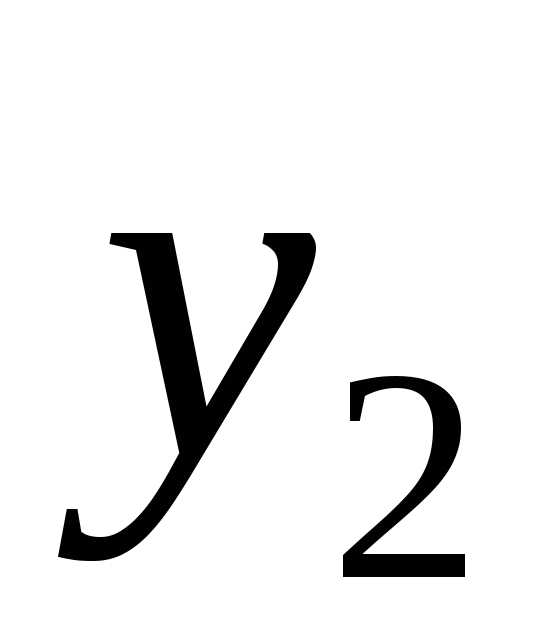
можно было взять в качестве базисных.
Симплексная таблица имеет вид
b | | | | |
L | 0 | -1 | -1 | 0 |
| -2 | -1 | 1 | -1 |
| -1 | -2 | -1 | 1 |
Таблица
двойственно-допустимая, но не оптимальная.
Выбираем ведущую строку – это строка
перемен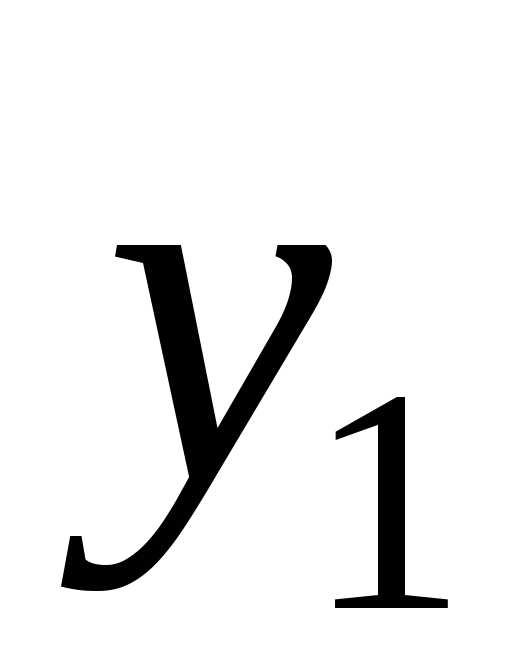ной 
,
ведущий столбец – это столбец переменной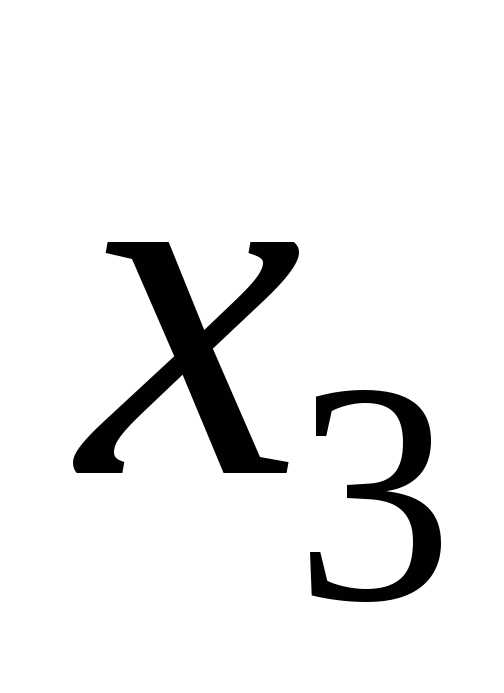
.
После преобразования таблица принимает
вид
b | | | | |
L | 0 | -1 | -1 | 0 |
| 2 | 1 | -1 | -1 |
| -3 | -3 | 0 | 1 |
Так
как в столбце b есть отрицательная переменная 
,
то эту строку выбираем ведущей, а столбец
переменной
будет ведущим столбцом. После преобразования
получаем таблицу:
b | | | | |
L | 1 | -1/3 | -1 | -1/3 |
| 1 | 1/3 | -1 | -2/3 |
| 1 | -1/3 | 0 | -1/3 |
которая является оптимальной. Соответствующее оптимальное решение имеет вид .
3. Двойственность в лп
3.1. Постановка задачи
Рассмотрим пару задач ЛП вида:
(I) (II)
… …
… …
… …
… …
.
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т. е. соотношение двойственности взаимное. Поэтому можно из такой пары задач любую считать прямой, а другую – двойственной.
studfiles.net