Построить плоскость по уравнению онлайн – 3D Calculator — GeoGebra

matworld.ru

Плоскость по трем точкам

Уравнение плоскости

Рассмотрим задачу построения уравнения плоскости   по  точкам в пространстве. Эта статья лишь вершина айсберга расчета поверхностей второго порядка в пространстве. Используется такая же методика что и в материале Расчет кривой второго порядка на плоскости

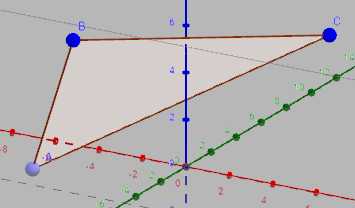
Уравнение плоскости в пространстве имеет вид

Легко заметить,  что раз тут три переменные, то мы однозначно определяем все значения плоскости по трем точкам.

Самый простой способ  определить уравнение плоскости это решить матричное уравнение

Проверим как это работает 

Пусть нам заданы три точки  с координантами P₀(1:-2:0) P₁(2:0:-1) и P₂(0:-1:2)

Подставив значения в уравнение получим.

Решая уравнение мы получим  вот такой результат

Наш бот, будет рассчитывать по своей методике и  при тех же самых данных,  мы получим  вот такое решение.

Читатель, может сразу заметить, что  коэффициенты при неизвестных совершенно другие чем  мы получили через матрицу.

Но тем не менее,  это одно и тоже уравнение плоскости. Достаточно лишь  умножить  правую и левую часть уравнения на 7

и получим 

Что подтверждает наши расчеты и правильность вычисления.

Если у вас в результате получилось например вот такое уравнение

А хочется получить все таки решение, где все значения в целых числах, рекомендую перевести числа в  дробь. Для этого достаточно посетить материал Непрерывные, цепные дроби онлайн или в случае когда результат  получается неудовлетоврительный,  Вычисление приближенной правильной дроби и каждое дробное значение превратить в дробь.

И наше уравнение превращается

И умножим правую и левую часть на 84 мы получим уравнение в целых числах.

Хотелось бы заметить только одно, три точки, которые Вы будете вводить, не должны быть на одной прямой, так как в таком случае, уравнение плоскости вычислить  неудастся в связи с неоднозначностью её положения в пространстве. 

Удачных расчетов!

• Площадь многоугольника по координатам онлайн >>

abakbot.ru

Решение уравнения плоскости онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Уравнение плоскости для 3 точек используется при применении метода координат для решения сложных задач. Данного рода уравнения не особо отличаются от уравнений прямой на плоскости, а именно оно и имеет вид:

\[Ax+By+Cz+D=0Ax+By+Cz+D=0Ax+By+Cz+D=0\]

\[A,B,C,D-A,B,C,D-A,B,C,D\] — числа

\[а x,y,z-x,y,z-~x,y,z\] — переменные

Так же читайте нашу статью «Решить уравнения высших степеней онлайн»

Например:

\[3x+2y-z+1=0, 0.5x-2z-2=0, x+y=03x+2y-z+1=0,~0.5x-2z-2=0,~x+y=03x+2y-z+1=0, 0.5x-2z-2=0, x+y=0 \]

Плоскость, как и любая другая геометрическая фигура, состоит из точек. В прямоугольной системе координат, например, \[Oxyz,\] каждой точке соответствует упорядоченная тройка чисел — координаты точки. Между координатами каждой точки плоскости можно установить зависимость с помощью уравнения, которое называют уравнением плоскости.

Уравнение плоскости в прямоугольной системе координат \[Oxyz\] в трехмерном пространстве — это уравнение с тремя переменными \[x, y и z,\] которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.

Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.

Где можно решить уравнение плоскости онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

общее, через три точки, нормальное

Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.

Итак, пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:

Чтобы получить уравнение плоскости, заданной этими условиями, и имеющее приведённый вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1), а для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е.

.

Вектор задан по условию. Координаты вектора найдём по формуле :

.

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

. (1)

Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используем формулу (1), еще раз посмотрим на неё:

.

В этой формуле числа A, B и C координаты вектора , а числа x0, y0 и z0 — координаты точки .

Вычисления очень простые: подставляем эти числа в формулу и получаем

.

Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:

.

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.

Итак, уравнение вида

    (2)

называется общим уравнением плоскости.

Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.

Как найти эти точки? Чтобы найти точку пересечения с осью Oz, нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0. Поэтому получаем z = 6. Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6).

Точно так же находим точку пересечения плоскости с осью Oy. При x = z = 0 получаем y = −3, то есть точку B(0; −3; 0).

И, наконец, находим точку пересечения нашей плоскости с осью Ox. При y = z = 0 получим x = 2, то есть точку C(2; 0; 0). По трём полученным в нашем решении точкам A(0; 0; 6), B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.

Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».

Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.

1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.

2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость параллельна оси Oz.

3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.

4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость — плоскости xOz.

5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 — координатную плоскость yOz.

Пример 3. Составить уравнение плоскости P, проходящей через ось Oy и точку .

Решение. Итак, плоскость проходит через ось Oy. Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P.

Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:

M0(2; −4; 3).

Среди них x = 2, z = 3. Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:

2A + 3C = 0.

Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем

A = −1,5C.

Подставив найденное значение A в уравнение , получим

или .

Это и есть уравнение, требуемое в условии примера.

Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение

Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .

Посмотреть правильное решение и ответ.

Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».

Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.

Используя выражение смешанного произведения в координатах, получим уравнение плоскости

    (3)

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.

Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:

, ,

и определить частный случай общего уравнения прямой, если такой имеет место.

Решение. По формуле (3) имеем:

Раскрываем определитель по первой строке:

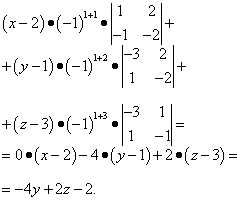
Получили общее уравнение плоскости

или после деления на -2:

.

Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.

Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».

Нормальным уравнением плоскости называется её уравнение, записанное в виде

,

где — направляющие косинусы нормали плоскости, — расстояние от начала координат до плоскости.

Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости — в трёх).

Пусть M — какая угодно точка пространства. Для нахождения отклонения точки M от плоскости следует в левую часть нормального уравнения плоскости подставить на место x, y и z подставить координаты этой точки.

Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.

,

так как расстояние не может быть отрицательным числом.

Общее уравнение плоскости

приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой

.

Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.

Пример 6. Привести уравнение плоскости к нормальному виду.

Решение. Вычислим нормирующий множитель:

.

Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:

.

Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3), а плоскость задана общим уравнением .

Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:

.

Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:

.

Вычислим отклонение точки от плоскости:

Найдём теперь расстояние от точки до плоскости как модуль отклонения:

Всё по теме «Прямая и плоскость»

• Плоскость
• Прямая в пространстве
• Задачи на плоскость и прямую в пространстве
• Прямая на плоскости

function-x.ru

Уравнение плоскости по трем точкам

Во многих стереометрических задачах, связанных с нахождением расстояния от точки до плоскости или расстояния между скрещивающимися прямыми, или угла между плоскостями, требуется найти уравнение плоскости. В этой статье я расскажу, как найти уравнение плоскости, если известны координаты трех точек, через которые она проходит.

Уравнение плоскости имеет вид: , где , , и  — числовые коэффициенты.

Пусть  нам нужно написать уравнение плоскости, которая проходит через точки , и  

Так как точки принадлежат плоскости, то при подстановке их координат в уравнение плоскости, мы получим верные равенства.

Так как у нас три точки, мы должны получить систему из трех уравнений с четырьмя неизвестными. Примем коэффициент  равным 1. Для этого разделим уравнение плоскости на  .  Получим:

Мы можем переписать  это уравнение в виде: 

Внимание! Если плоскость проходит через начало координат, то принимаем d=0.

Чтобы найти коэффициенты А, В и С, подставим координаты точек , и   в уравнение плоскости .

Получим систему уравнений:

Решив ее, мы найдем значения коэффициентов А, В и С.

Решим задачу.

В правильной четырехугольной призме  со стороной основания 12 и высотой 21 на ребре  взята точка  так, что  равно 8. на ребре  взята точка  так, что  равно 8. Написать уравнение плоскости :

Поскольку для нахождения уравнения плоскости нам понадобятся координаты точек, я сразу помещаю призму в систему координат:

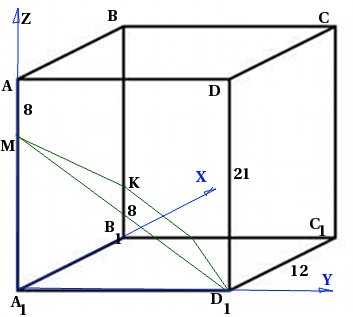
Запишем координаты точек:

Подставим их в систему уравнений:

Отсюда:

Подставим найденные коэффициенты в уравнение плоскости:

Чтобы избавиться от дробных коэффициентов, умножим обе части уравнения плоскости на . Получим:

Ответ: уравнение плоскости   

И.В. Фельдман, репетитор по математике.

ege-ok.ru