1.5. Предметные операции на множествах. Формула множества
Для того чтобы можно было конструировать множества сложной структуры (составные) из некоторых исходных (простых), на них вводятся предметные операции. Рассмотрим их.
Определение. Объединением множеств А и В называют множество С, содержащее элементы, входящие хотя бы в одно из них. Обозначают как С = АВ ={x (xA) или (xB)}.
Пересечением множеств А и В называют множество С, содержащее элементы, входящие одновременно в А и В. Обозначают: С = АВ ={x (xA) и (xB)}.
Разностью
Симметрической разностью множеств А и В называют множество С, содержащее элементы из А\В и из В\А. Обозначают: С = АВ =(А\В) (В\А) .
Рассмотрим множества, состоящие из объектов некоторого вида, содержащихся в заданном универсальном множестве U. Дополнением множества А называют множество С, содержащее элементы из U, не входящие в А. Обозначают дополнение: С=А либо С = А.
Дополнение любого множества можно представить как результат его вычитания из универсального: А = U \ А.
Результатом выполнения рассмотренных предметных операций (, , \, , ) всегда является множество.
Определение. Формулой множества называется:
1) любое выражение вида А, В, С,…, где А, В, С,…— обозначения простых множеств, заданных непосредственным определением;
2) любое выражение вида АВ; АВ; А\В; АВ; А, где А, В — формулы множеств.
Графически множества изображают в виде плоских фигур (кругов, овалов и т.д.). Такие изображения называют диаграммами Венна. На диаграммах а) — д) рис.1.1 показаны результаты выполнения введенных выше операций объединения, пересечения, разности, симметрической разности и дополнения.
Для упрощения записи выражений, содержащих операции на множествах, обычно принимают, что самой сильной операцией (выполняющейся ранее других, если другой порядок не оговорен скобками) является отрицание. Второй по силе операцией является пересечение, остальные
Рис.1.1
Пример 1.
1. АВС — формула множества, которую с учетом введенного старшинства операций следует понимать как А(ВС).
2. С А — запись не является формулой множества, так как в ней одноместная операция дополнения соединяет два множества.
Для наиболее полной характеристики содержательного смысла формулы составного множества F, в которую входят простые множества А1, А2,…, Аn, рассмотрим множество {R} всех возможных пересечений простых множеств либо их дополнений { А1 1 А22 … Аn n}, где i = 0 или 1, Аi1 = Аi, Аi0= Аi. Представляя вектор индексов (1,2,…,n) в виде записи двоичного числа N в промежутке от 0 до 2n–1, упорядочиваем по возрастанию этих чисел все элементы {R}. Назовем их элементарными пересечениями. Эти пересечения для двух и трех простых круговых множеств даны в виде диаграмм Венна на рис. 1.2.
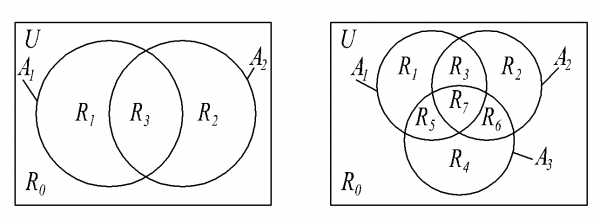
Рис.1.2
Диаграммы Венна для заданного числа исходных множеств, на которых показаны все их возможные элементарные пересечения, назовем полными диаграммами пересечений. Такие диаграммы с круговыми изображениями исходных множеств могут быть построены только для двух и трех множеств (рис.1.2). При четырех и выше необходимо использовать вместо кругов более сложные фигуры.
Таблицы с упорядоченными по возрастанию чисел N элементарными пересечениями для двух и трех простых множеств имеют вид:
N | А2 | А1 |
0 | 0 | 0 |
1 | 0 | 1 |
2 | 1 | 0 |
3 | 1 | 1 |
N | А3 | А2 | А1 |
0 | 0 | 0 | |
1 | 0 | 0 | 1 |
2 | 0 | 1 | 0 |
3 | 0 | 1 | 1 |
4 | 1 | 0 | 0 |
5 | 1 | 0 | 1 |
6 | 1 | 1 | 0 |
7 | 1 | 1 | 1 |
Любой формуле составного множества F(А1, А2,…, Аn) можно взаимно однозначно поставить в соответствие вектор, отражающий вхождение в него элементарных пересечений {R}. Назовем его вектором включений. Если формула имеет сложный вид, построение данного вектора можно проводить поэтапно. При объединении двух множеств в итоговом векторе включений учитываются единицы из обоих векторов, при пересечении остаются только единицы, входящие одновременно в оба вектора. При применении отрицания в векторе происходит замена 0 на 1 и 1 на 0. При вычитании
Пример 2. Построить векторы включений для составных множеств, заданных на простых множествах А и В следующими формулами: 1) F1 = (АВ), 2) F2 = (АВ), 3) F3 = АВ (АВ). Результаты привести в таблице.
Решение. При определении векторов включений используем старшинство операций. Вектор для F1 строим поэтапно, используя объединение АВ. Вектор включений для F2 находим с использованием формулы АВ =( А\В) (В\А) . В случае F3 рассматриваем предварительно векторы формул АВ, АВ и (АВ).
N | А | В | А В | F1 | А В | F2 | А В | (А В) | F3 |
0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
2 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
3 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Данную конструкцию назовем таблицей пересечений.
ЗАДАЧИ
1. Определить, будут ли следующие выражения формулами множеств:
а) АС\; б) А В; в) ( АC); г) С?
2. Указать очередность выполнения операций в формулах:
а) А ВС; б) А С; в) АВСD.
3. Построить таблицы пересечений и изобразить все элементарные пересечения на полных диаграммах пересечений для составных множеств, заданных формулами:
а) (АВ)\С; б) (АВС) ; в) А (В С) ; г) (АВ) (А\ С) ; д) А В С (В С).
4. Привести примеры непустых исходных множеств А, В, С, при которых будет выполняться равенство составных множеств:
а) АВ и АВ; б) А \ ( ВС) и А\В.
studfiles.net
Определение мощности множества всех подмножеств конечного множества (с использованием формулы бинома Ньютона)
Пусть А произвольное конечное n- элементное множество. Найдем мощность множества P(A), |P(А)|= , где S={0,1,…,n}.
Для определения величины |Р(А)| воспользуемся формулой бинома Ньютона.
, при условиях, что a=в=1.
Получаем, =|P(A)|.
Замечание.
Множество называется булеаноммножества А.
Понятия алгебраических и кардинальных операций. Алгебраические операции над множествами. Покрытие и разбиение множества.
Алгебраическимиоперациями называют такие, при выполнении которых результирующее множество либо пусто, либо состоит из элементов, из которых состоят и множества, подвергающиеся операциям.
Кардинальными операциями называют такие операции, при выполнении которых появляются новые элементы.
Основными алгебраическими операциями над множествами являются следующие:
— пересечение множеств,
— объединение множеств.
-разность множеств.
Пусть А и В — произвольные множества. Их пересечением называется множество
А В={x| x A и x B}.
Объединениеммножеств А и В называется множество
А В={x|x A или x B}.
Разностьюмножеств А и В называется множество А\В={x|x A, но x B}.
Используя понятие универса, можно ввести еще две операции над множествами — дополнение и симметрическую разность множеств.
Дополнением множества А (до универса J) называется множество =J\A, т.е. ={x| x J, но x A}.
Симметрической разностьюмножеств А и В называется множество
А В=(A\B) (B\A).
Если А В= , то говорят, что множества А и В не пересекаются.
Если X — некоторое множество и X=A В … С, то множества А,В,…,С образуют покрытие множества X. Если при этом все множества А,В,…,С попарно не пересекаются, то система множеств А,В,…,С называется разбиением множестваX.
Поэлементное доказательство теоретико-множественных равенств.
Пусть А и В некоторые множества. Для того, чтобы проверить являются ли они равными, необходимо установить два соответствия : А В и В А.
Для установления соответствия А В необходимо показать, что текущий (т.е. произвольный) элемент множества А принадлежит множеству В. Такое доказательство называется поэлементным.
Покажем, например, справедливость утверждения:
(А В)\ (А В)= (А\В) (В\А).
Пусть N=(А В)\(А В), M=(А\В) (В\А).
Надо показать, что NM и MN.
Покажем, что NM.
Пусть x N, т.е. x (А В), но x (А В).
Если x А и x (А В), то x В, а отсюда x B\A.
Если x B и x (А В), то x A, а отсюда x A\B.
Получили, что всегда x принадлежит либо (А\В) либо (В\А), т.е x M.
Покажем, что MN.
Пусть x M, т.е. x А\В или x В\А.
Если x А\В, то x А и тем самым x А В.
Так как x В, то x А В, а тем самым x (А В)\ (А В)=N.
Аналогично доказывается и для случая x В\А.
megaobuchalka.ru
§3. Непротиворечивые и полные множества формул.
Определение
4: а) Пусть
S-произвольное
множество предложений сигнатуры  .
.
Множество
S
называется выполнимым, если существует
модель <M,  >,
в которой истинны все предложения из
множества S.
>,
в которой истинны все предложения из
множества S.
В противном случае, множество S-не выполнимое.
б)
Множество S
называется противоречивым,
если существует такое предложение A
сигнатуры
,
что из множества S
мы выводим одновременно A
и  A,
то есть S
├ (A&
A,
то есть S
├ (A& )
)
В противном случае, множество S называется не противоречивым.
Пусть
множество S-
выполнимое. Это означает, что мы можем
придать множеству S
такое содержание, при котором все
предложения множества S
будет истинны. Относительно такого
момента говорят: рассуждение S
имеет смысл. И наоборот, если некоторое
рассуждение S
кажется неправдоподобным, говорят: оно
бессмысленно. Поэтому понятие выполнимого
множества предложений является
математическим определением, содержательно
правильного рассуждения. В этом отношении
понятие непротиворечивого множества
предложений является математическим
определением формального правильного
рассуждения. Если в процессе некоторого
рассуждения S
получается противоречие типа A& ,
то это рассуждение естественно считать
не правильным. Если рассуждение не
противоречиво, естественно его считать
правильным.
,
то это рассуждение естественно считать
не правильным. Если рассуждение не
противоречиво, естественно его считать
правильным.
Теорема 7. Если множество предложений S выполнимо, то оно не противоречиво.
Доказательство: Пусть множество S имеет модель H, в которой истинны все предложения из S.
Предположим
от противного, что S-противоречиво.
Это означает, что существует такое
предложение A,
которое выводится своим прямым и обратным
значением из S,
то есть S├
(A& )
)
По теореме 2 §3 гл.3, теореме 5 §2 гл.1, аксиомы ИП являются тавтологиями и поэтому истинны модели M.
По
теореме 4 §2 гл.1, теореме 3 §3 гл3, правило
вывода, МР,  -правило,
-правило, -правило,
примененные к истинным формулам, снова
дают истинные формулы (*).
-правило,
примененные к истинным формулам, снова
дают истинные формулы (*).
Поскольку, предложение из S истинны в модели М, то полученный с помощью вышеуказанных правил(*) предложения такие будут истинными в модели М.
(A& )
)  И
И
Но это противоречит теореме 1[§3 гл3]
Таким образом, ты доказали, что содержательное понятие правильности рассуждения полностью согласуется с формальными.
Представляет интерес обратное утверждение: верно ли, что всякое формальное правильное рассуждение, является содержательно правильным? Другими словами: верно ли, что каждое не противоречивое множество предложений выполнимо?
Определение 5: Счетным множеством мы называем множество, каждому элементу которого можно сопоставить какое-либо число.
Лемма I.Если
сигнатура  счетно, то множество всех формул
счетно, то множество всех формул  также счетно.
также счетно.
Лемма II.
Пусть S0,S1,S2,…,S есть непротиворечивые множества предложений.
Пусть
S0 S1
S1 S2
S2 …
предложения вложены, тогда множество
T
вида:
…
предложения вложены, тогда множество
T
вида:
T
= 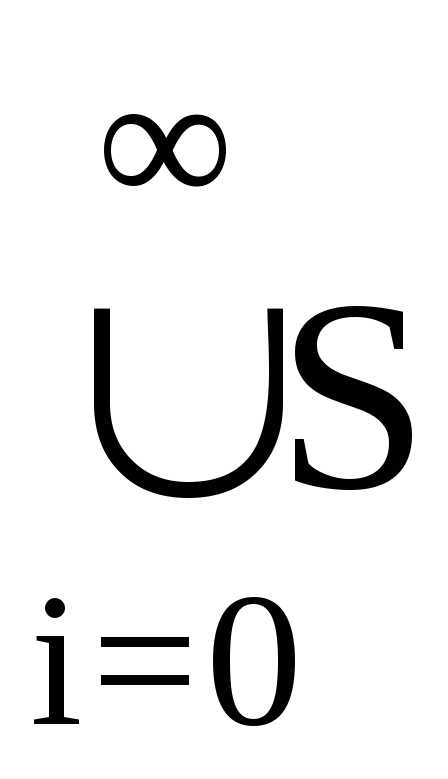 i также непротиворечиво.
i также непротиворечиво.
Доказательство: метод от противного: предположим, что Т – противоречиво. Тогда существует такое предложение А, что в
Т├
(A& )
)
Вывод
A& представляет собой конечный набор
формул и поэтому использует лишь конечное
число гипотез из Т.
представляет собой конечный набор
формул и поэтому использует лишь конечное
число гипотез из Т.
В
свою очередь все эти гипотезы попадают
в некоторое предложение Si.
Тогда очевидно, что Si порождает A& ,
то есть
,
то есть
Si├
(A& )
)
Но это не возможно потому что по условию Si – противоречиво.
Лемма III. Если S
– непротиворечивое множество предложений,
А- произвольное предложение, то хотя бы
одно из множеств S
U{A}
или S
U{ }
является непротиворечивым.
}
является непротиворечивым.
Доказательство: метод от противного.
Предположим,
что S
U{A},
S
U{ }
– противоречивы, тогда существуют такие
предложенияB
и C,
что S,
A
├ (B&
}
– противоречивы, тогда существуют такие
предложенияB
и C,
что S,
A
├ (B& )
и S,
)
и S,  ├ (C&
├ (C& )
)
На основании определения 8:
(B& )
├ (C&
)
├ (C& )
либо (C&
)
либо (C& )
├ (B&
)
├ (B& )
)
Тогда по правилу силлологиза следует:
S,  ├ (C&
├ (C& )
)
S,
A├
(C& )
правило удаления
)
правило удаления  :S(A
:S(A
 )
├ (C&
)
├ (C& )
)
Но
(A
 )
является доказуемой в ИП. Следовательно,
исходное множествоS
обеспечивает выводимость(*):
)
является доказуемой в ИП. Следовательно,
исходное множествоS
обеспечивает выводимость(*):
S├
(A
 )
) (C&
(C& )
(*)
)
(*)
Но (*) невозможно, т.к. по условию множество S – непротиворечиво.
Определение
6. Множество
Т сигнатуры  называется полным в сигнатуре
называется полным в сигнатуре  ,
если для каждого предложения A
сигнатуры
,
если для каждого предложения A
сигнатуры  выполняется:
выполняется:
T
├ A
, либо T
├
Данное определение означает, что полное множество Т нельзя расширить никакими предложениями данной сигнатуры, которые не были бы выводимы из T.
Если
некоторое множество предложений А
сигнатуры  не выводимо из T,
то тогда, очевидно, что из Т выводится
его отрицание. Но тогда, очевидно, T
не выводимо из T,
то тогда, очевидно, что из Т выводится
его отрицание. Но тогда, очевидно, T {A}
будет противоречивым.
{A}
будет противоречивым.
Следующая теорема утверждает, что любое множество предложений можно расширить до полного и непротиворечивого множества.
Теорема Линдепбаума. Всякое непротиворечивое множество предложений S содержится в непротиворечивом и полном множестве предложений T той же сигнатуры.
Доказательство:
Пусть
S-
непротиворечивое множество предложений
сигнатуры  .
Пронумеруем все предложения данной
сигнатуры A1,…,An,
An+1,…
(1)
.
Пронумеруем все предложения данной
сигнатуры A1,…,An,
An+1,…
(1)
Индукцией по n построим последовательность: S0, S1,…, Sn, Sn+1,… (2)
Очевидно,
T
= 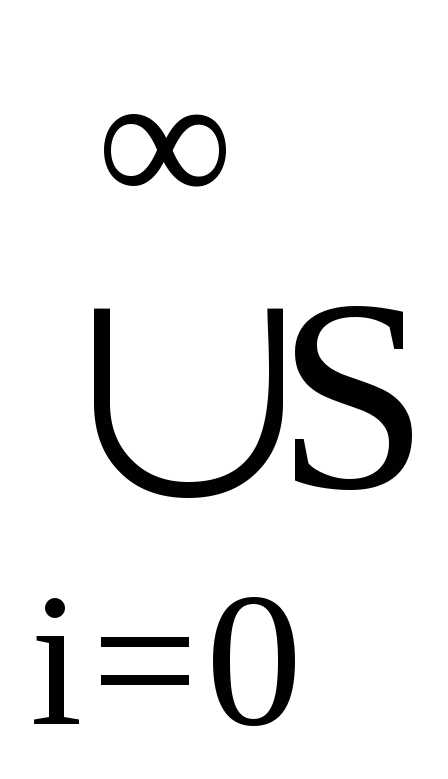 i
i
Имеет место:
1) S0=S
2) Пусть Sn-определено
3) Положим Sn+1 = а)Sn U{An+1},если Sn U{An+1} — непротиворечиво
б)
Sn
U{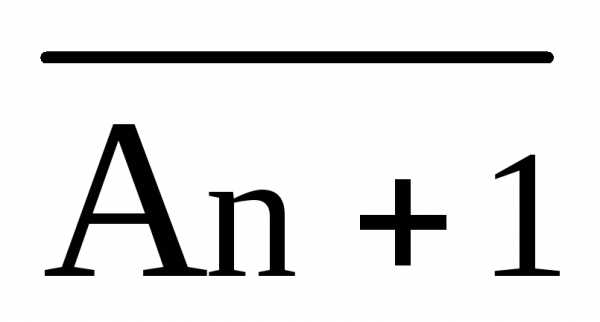 },
в противном случае
},
в противном случае
Договорившись о такой конструкцией индукции предложения (2) мы можем утверждать Sn+1(n>2) получается из предыдущего множества Sn путем добавления конкретного множества (An+1) или его отрицания.
Поэтому
в последовательности (4) мы можем
расставить такую связь S0 S1
S1 S2
S2 …
… Sn
Sn Sn+1
Sn+1 …,
…,  n
(An
n
(An Sn)
или
(
Sn)
или
( n
n Sn)
Sn)
Необходимо доказать, что Sn-непротиворечиво.
Заметим:
1) S0=S – непротиворечиво по условию;
2) Предположим, Sn – непротиворечиво;
Рассмотрим Sn+1=Sn U {An+1}
Если Sn U {An+1} – непротиворечиво, то Sn+1 – является тоже непротиворечивым.
Если
Sn
U{An+1}
– противоречиво, то по лемме 3 Sn U{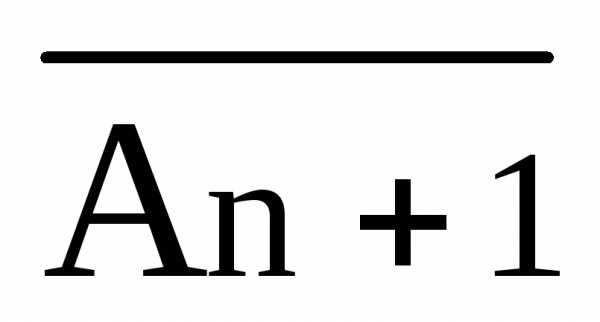 }-является
непротиворечивым.
}-является
непротиворечивым.
Если
Sn+1 = Sn U{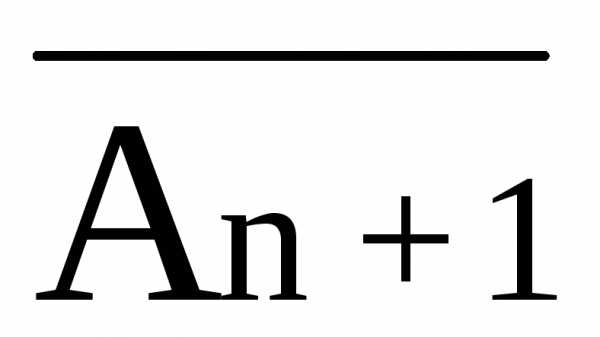 },
то выражение (4) удовлетворяет лемме 2 и
множество T=
},
то выражение (4) удовлетворяет лемме 2 и
множество T=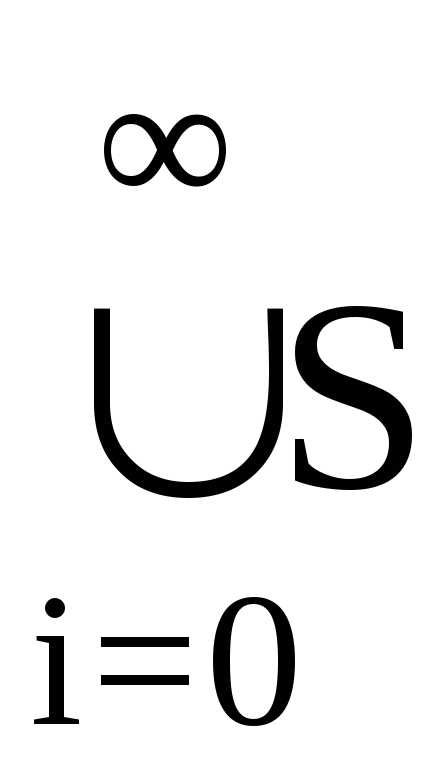 n является искомым.
n является искомым.
Действительно, относительно множества Т заметим:
оно непротиворечиво
оно
полно, т.е. каждое предложение А сигнатуры  совпадает с некоторым предложением An
из выражения (3): (A
совпадает с некоторым предложением An
из выражения (3): (A Sn)
или (
Sn)
или (
 Sn)
Sn)
Это
влечет либо выводимость Т├A,
либо Т├ .
На основании этого, можем утверждать:
Т – полное множество сигнатуры
.
На основании этого, можем утверждать:
Т – полное множество сигнатуры  .
.
studfiles.net
1.7. Алгебра множеств. Ее формулы, теоремы и законы
В математике алгеброй называют множество объектов с введенными на них операциями.
Определение. Алгеброй множеств называют совокупность множеств и операций над ними — предметных (, , \, , ) и сравнения ( , , = ), а также отрицаний операций сравнения.
В алгебрах выражения над объектами, правильно записанные при помощи введенных операций, называют формулами.
Определение. Формулой алгебры множеств называют любое выражение вида А В, где А, В — формулы множеств, — операция сравнения либо ее отрицание.
Формулы, справедливые для любых входящих в них множеств, называются теоремами алгебры множеств. Они задают всегда верные рассуждения о множествах. Количество всех возможных теорем алгебры множеств бесконечно.
Пример 1. Рассмотрим следующие выражения:
а) (АВ) = А В; б) АВ = АВ;
в) АВ АВ; г) (АВ) С = (АC) (BС).
Выражение а) не является формулой алгебры множеств, так как в правой части его стоит выражение, не являющееся формулой множества. Выражения б) и в) — формулы алгебры множеств. Как нетрудно показать на примерах, равенство б) справедливо только в одном случае, когда А = В, в других случаях оно ложно. Поэтому оно не будет теоремой. Нестрогое включение в) и равенство г) выполняются всегда, поэтому они являются теоремами алгебры множеств.
Среди теорем особо выделяют такие, где используется операция сравнения «равенство» ( = ), поскольку такие теоремы задают эквивалентные преобразования формул (не нарушающие их истинности). Наиболее употребительные теоремы с равенствами называют законами алгебры множеств. В качестве законов обычно приводят следующие теоремы:
1. Коммутативные законы — действуют относительно операций объединения и пересечения.
АВ =ВА; АВ =ВА.
2. Ассоциативность (для операций объединения и пересечения).
(АВ)С =А(ВС) =АВС);
(АВ)С =А (ВС) =А ВС.
3. Дистрибутивные законы.
(АВ)С =(АC)(BС);
(АВ)С=(АC)(BС).
4. Идемпотентность.
АА =А ; АА =А.
5. Поглощение.
А(АВ)= АВ; А(АВ) =АВ.
6. Законы де Моргана.
(АВ) = А В; (АВ)= А В.
7. Закон исключения третьего.
А = А.
8. Операции с пустым и универсальным множествами.
(АU) =U; (А) =A;
(АU) =A; (А) = ;
(U) =; (U) = U;
=U; U = .
Рассмотрим проверку правильности рассуждений о множествах, задаваемых формулами алгебры множеств. В общем случае она может быть выполнена с использованием полных диаграмм пересечений, а также с помощью векторов включений.
Пример 2. Проверить справедливость первого закона де Моргана: (АВ) = А В.
Решение. Необходимо выяснить равенство в общем случае составных множеств, заданных формулами F1 = (АВ) и F2 = А В. Построим на полных множествах элементарных пересечений векторы включения для F1 и F2:
N | А | В | АВ | F1 | А | B | F2 |
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
2 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Так как данные векторы совпадают, то составные множества, заданные формулами F1 и F2, равны при любых входящих в них множествах А и В. Рассмотренное равенство является теоремой алгебры множеств.
Также строгое доказательство закона можно дать на полной диаграмме пересечений для двух множеств (рис.1.2).
Для доказательства того, что некоторая формула не является теоремой алгебры множеств, достаточно указать хотя бы один случай её нарушения — например, на конкретных множествах или на диаграммах Венна, которые не обязательно должны быть полными диаграммами пересечений.
Пример 3. Будет ли теоремой формула А\В = (АВ)?
Решение. Проверка на диаграмме Венна для произвольных множеств U, A, B (рис. 1.3) показывает, что формула дала неверный результат, следовательно, она не будет теоремой.
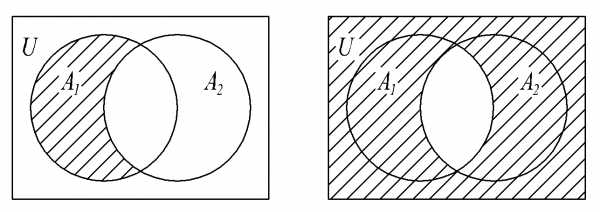
Рис.1.3
Замечание Доказанный выше факт не означает, что конкретные составные множества, задаваемые формулами (АВ) и А\В, всегда не равны. Например, в частном случае при A=U равенство выполняется, поскольку А\В= В, (АВ) = В.
ЗАДАЧИ
Выразить аналитически в виде формул множества а)—ж) (рис.1.4), указанные на диаграммах Венна штриховкой:
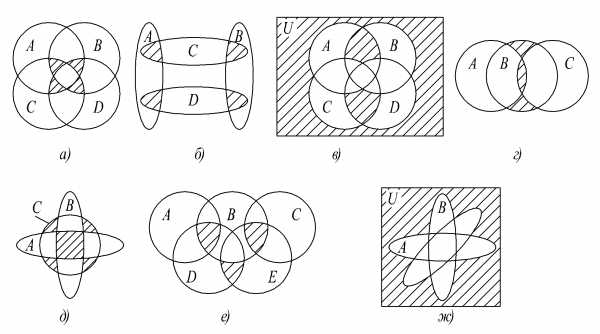
Рис. 1.4.
2. Изобразить, используя полные диаграммы пересечений Венна, множества, заданные формулами:
а) (АВ) (СВ), б) А (ВС), в) АВ, г) ( (А\В)\С), д) ( А В), е) ( А \ В), ж) ( ( АВ)\ С), з) А (С В) , и) (АВ) (В С).
3. Сравнить следующие пары составных множеств, заданные формулами:
а) (АВ) и А B, б) (АВ) (AC) и (BA) (BC), в) (A\B) B и А B, г) АB и (А\B) B, д) (AB)\С и (А\(BC)) (В\ (AC)).
4. Проверить (доказать или опровергнуть), будут ли приведенные ниже формулы теоремами алгебры множеств:
а) (AB) (AВ) = ( АВ), б) А(В\A) = , в) А\(ВС) = А (ВС), г) (AB) A = A, д) (A B)\С = (А\(BC)) (В\ (AC)), е) A B АB , ж) А\(BC) В, з) АВ (AB) C, и) АВ (ABC).
studfiles.net
Лекция 2.Декартово произведение. Мощность множества
2. Декартово произведение. Мощность множества.
2.1. Декартово произведение множеств.
Упорядоченная пара 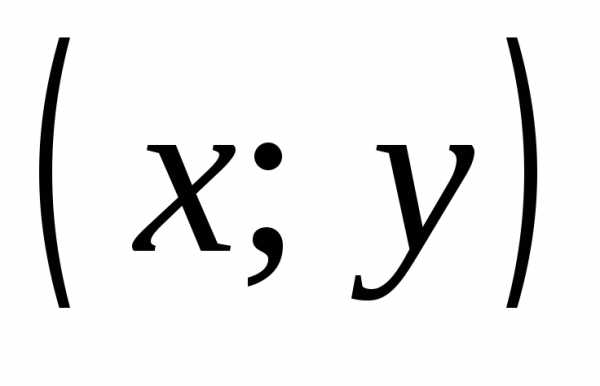 определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары
определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары 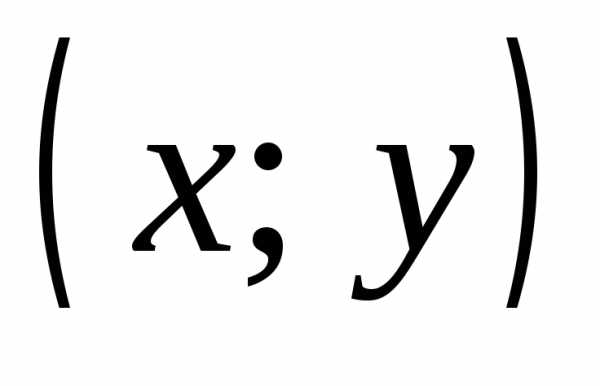 и
и 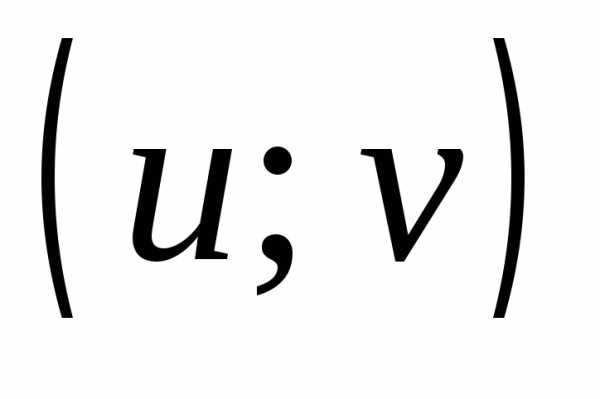 считаются равными тогда и только тогда,
когда x=u и y=v.
считаются равными тогда и только тогда,
когда x=u и y=v.
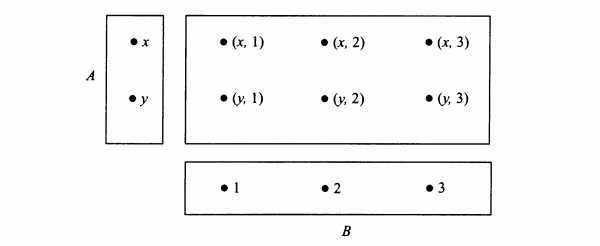
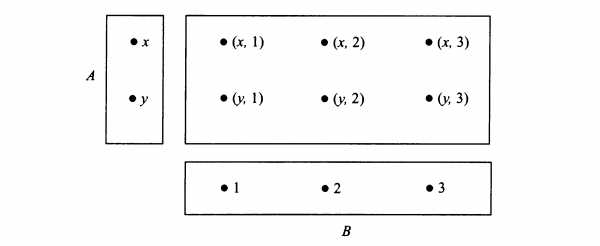
Определение 2.1. Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество всех упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B:
.
Пример .. Пусть 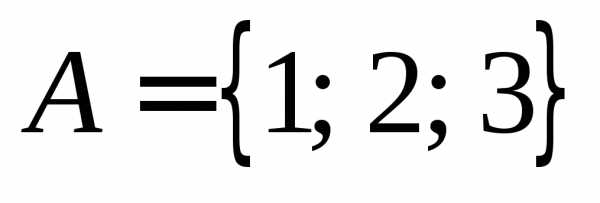 и
и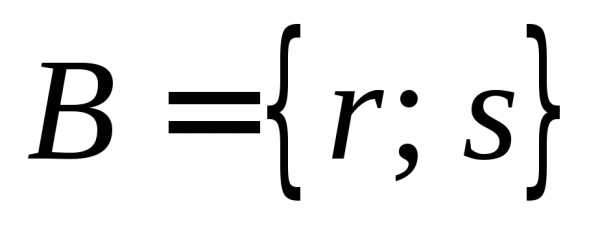 .
Тогда
.
Тогда
.
.


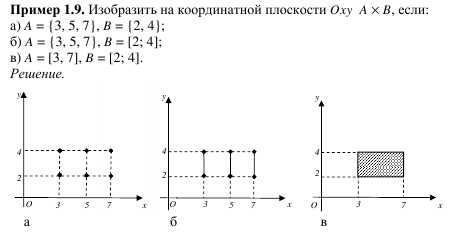
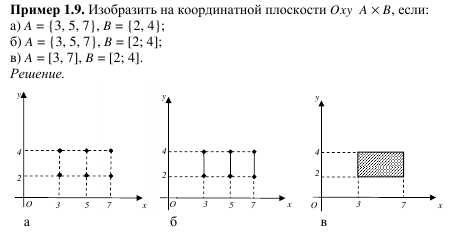
Пример .. На координатной плоскости построить следующее множество:
(-1; 3×1; 3)
Решение. Первое множество помещаем на оси OX, второе на оси OY. Множество всех пар, т.е. декартово произведение, изображается точками заштрихованного прямоугольника, но без левой и нижней стороны.
В общем случае, точка на плоскости может быть задана упорядоченной парой координат, то есть двумя точками на координатных осях. Поэтому координатную плоскость можно задать в виде . Метод координат ввел в употребление Рене Декарт (1596-1650), отсюда и название «декартово произведение».
Диаграмма Венна, иллюстрирующая декартово произведение АхВ
В частности, если A пусто или B пусто, то, по определению, AB пусто.
Понятие прямого произведения допускает обобщение.
Прямое произведение множеств A1, A2, …, An – это множество наборов (кортежей):
.
Множества Ai не обязательно различны.
Степенью множества A называется его прямое произведение самого на себя. Обозначение:
.
Соответственно, и вообще.
Пример .. Пусть B=0, 1. Описать множество Bn.
Решение. Множество Bn состоит из последовательностей нулей и единиц длины n. Они называются строкой бит или битовой строкой длины n.


2.2. Мощность множества.
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если каждому элементу множества A соответствует один и только один элемент множества B и каждому элементу множества B соответствует некоторый элемент множества A. В этом случае говорят также, что множества A и B изоморфны и используют обозначение AB.
Определение 2.2. Два множества A и B называются эквивалентными, или равномощными, если между этими множествами может быть установлено взаимно однозначное соответствие. В этом случае пишут: AB, или A=B, и говорят, что множества A и B имеют равные мощности.
Пример ..
1) Множество десятичных цифр равномощно множеству пальцев на руках человека.
2) Множество четных натуральных чисел (2N) равномощно множеству всех натуральных чисел (N).
Определение 2.3. Множество A называется конечным, если оно эквивалентно Jn при некотором n, где Jn=1, 2, …, n – множество n первых натуральных чисел.
Определение 2.4. Мощностью конечного множества A, которое содержит k элементов, называется число его элементов. Она обозначается A=k. Пустое множество считается конечным с числом элементов равным нулю, т.е. =0.
Таким образом, если множество A конечно, т.е. A=k, то элементы A всегда можно перенумеровать, то есть поставить в соответствие элементам номера из отрезка натурального ряда 1..k с помощью некоторой процедуры. Наличие такое процедуры подразумевается, когда употребляется запись A=a1, a2, …, ak.
Пример .. В компьютере все множества реальных объектов конечны: множество адресуемых ячеек памяти, множество исполнимых программ, множество тактов работы процессора.
Множества, которые не являются конечными, называются бесконечными. Если некоторое множество A равномощно множеству натуральных чисел N, т.е. AN, то множество A называется счетным. Счетное множество A – это такое множество, все элементы которого могут быть занумерованы в бесконечную последовательность a1, a2, …, an, …, так, чтобы при этом каждый элемент получил лишь один номер n и каждое натуральное число n было бы номером лишь одного элемента множества A.
Мощность счетного
множества принято обозначать через 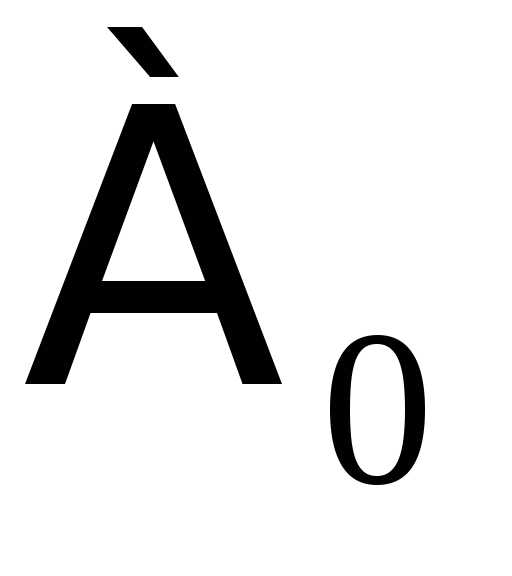 (
( – первая буква древнееврейского
алфавита, называемая «алеф», символ
– первая буква древнееврейского
алфавита, называемая «алеф», символ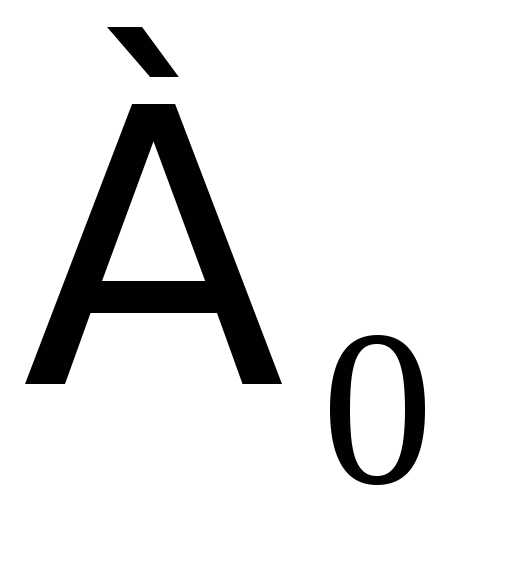 читается: «алеф-нуль»).
читается: «алеф-нуль»).
Наименьшая бесконечная мощность – мощность множества натуральных чисел
N=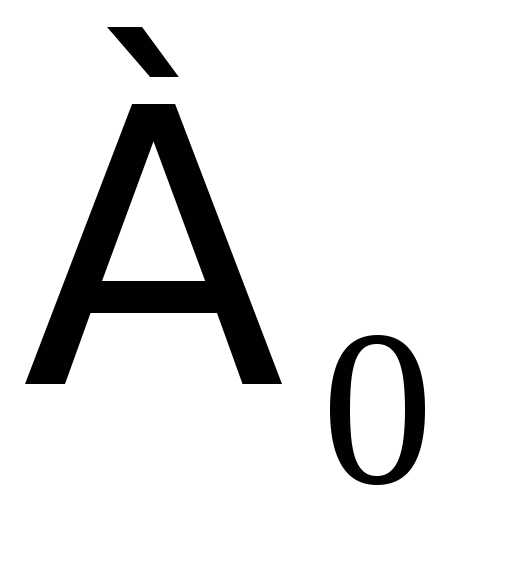 .
.
Пример .7. Множество Z – множество целых чисел также счетно.
Решение. Рассмотрим множество целых чисел Z:
…, n, …, 3, 2, 1, 0, 1, 2, 3, …, n, … .
На первый взгляд, кажется, что это множество невозможно перенумеровать. Однако эту нумерацию можно осуществить, применив следующую хитрость: двигаясь не в одном направлении, а все время менять его.
Иными словами, будем нумеровать так: числу 0 дадим номер 1, числу 1 – номер 2, числу 1 – номер 3, числу 2 – номер 4, числу 2 – номер 5, и т.д. Таким образом, получаем взаимно однозначное соответствие между множеством Z и N. А значит, множество Z счетно.
Множество A называется несчетным,
если его мощность больше мощности
множества N.
В таком случае множество A называется континуальным или континуумом.
Мощность континуума обозначается 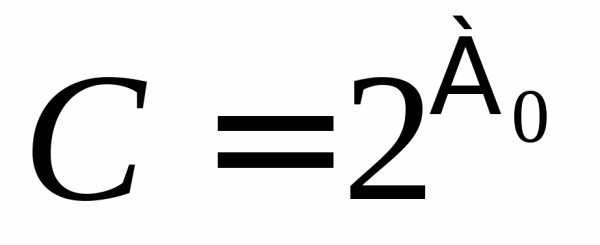 .
Следующую теорему примем без доказательства.
.
Следующую теорему примем без доказательства.
Теорема 2.1. Множество всех действительных чисел имеет мощность континуума, т.е. R=C.
2.3. Теоремы сложения и умножения.
Формула включений и исключений.
Теорема 2.2. (Теорема сложения)
Пусть – конечные попарно непересекающиеся множества, т.е.. Тогда
(2.3.1.)
Доказательство. Докажем теорему методом математической индукции.
Базис индукции. Пусть n=2. Пусть множества X1=A и X2=B, мощности которых соответственно равны k1 и k2, т.е. A=k1, B=k2. Так как AB=, то
.
Индуктивный переход. Пусть теорема верна для n. Покажем, что для n+1 будет тоже справедливо. Тогда
Теорема 2.3. (Теорема умножения)
Пусть заданы конечные множества . Тогда
(2.3.2.)
т.е. число элементов декартова произведения множеств равно произведению количеств элементов сомножителей.
Доказательство. Докажем теорему методом математической индукции.
Базис индукции. Пусть n=2. Пусть множества X1=A и X2=B, мощности которых соответственно равны k1 и k2, т.е. A=k1, B=k2. Первый компонент упорядоченной пары можно выбрать k1 способами, второй – k2 способами. Таким образом, всего имеется k1k2 различных упорядоченных пар. Значит,
.
Индуктивный переход. Утверждение теоремы справедливо для n. Покажем, что оно будет справедливо и для n+1. Имеем:
Пример .. Сколько существует целых чисел между 0 и 1000, содержащих ровно одну цифру 6?
Решение. Пусть S – множество целых чисел между 0 и 1000, содержащих ровно одну цифру 6. Рассмотрим три подмножества S1, S2 и S3 множества S.
S1 – множество, которое содержит число, состоящее из одной цифры, и эта цифра 6;
S2 – множество, содержащее двузначные числа ровно с одной цифрой, равной 6;
S3 – множество, содержащее трехзначные числа ровно с одной цифрой, равной 6.
Множество S1 содержит только один элемент – число 6. Значит, S1=1.
В множестве S2 каждый элемент, содержащей 6, имеет ее либо первой, либо второй цифрой. Если 6 – вторая цифра, то существует 8 различных чисел, которые будут стаять на первом месте, поскольку первое число не может быть 0 или 6. Если 6 – первая цифра, то таких чисел 9, поскольку вторая цифра не может быть 6. Таким образом, S2 содержит 8+9=17 элементов, т.е. S2=17.
Элемент из S3 содержит 6 как первою, вторую или третью цифру.
Если 6 – первая цифра, то существует 9 вариантов выбора второй цифры и 9 вариантов выбора третьей цифры. Согласно комбинаторному принципу умножения, S3 содержит 99=81 чисел с первой цифрой 6.
Если 6 – вторая цифра, то имеются 9 вариантов выбора третьей цифры и 8 вариантов выбора первой цифры, поскольку первая цифра не может быть нулем. Следовательно, S3 содержит 98=72 числа, у которых 6 – вторая цифра.
Аналогично, S3 содержит 72 числа, у которых 6 – третья цифра. Следовательно, всего S3 содержит 81+72+72=225 элементов, т.е. S3=225.
Поскольку и множестваS1, S2 и S3 попарно непересекающиеся, то
.
Поставим задачу подсчитать число элементов в объединении
X=X1X2…Xm
конечных
множеств  ,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
Теорема 2.4. (Формула включений и исключений).
Для конечных множеств  ,
справедлива формулавключений
и исключений.
,
справедлива формулавключений
и исключений.
(2.3.3.)
В частности для двух множеств эта формула примет вид:
.
Для трех множеств формула включений и исключений примет вид:
.
Название этой теоремы подчеркивает использование последовательных включений и исключений элементов подмножеств.
Пример .. Сколько положительных целых чисел, меньших 101, делятся на 2 или на 3?
Решение. Пусть X – множество положительных целых чисел, которые делятся на 2 или 3. Рассмотри два подмножества X1 и X2 множества X.
X1 – множество положительных целых чисел,
которые делятся на 2. Число элементов
или мощность этого множества равно 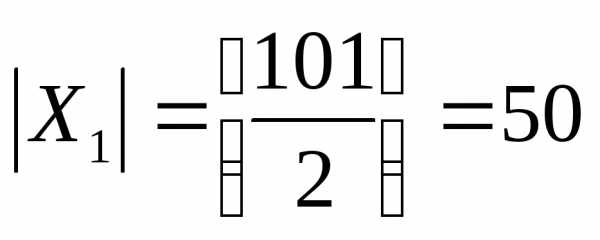 .
.
X2 – множество положительных целых чисел,
которые делятся на 3. Число элементов
или мощность этого множества равно 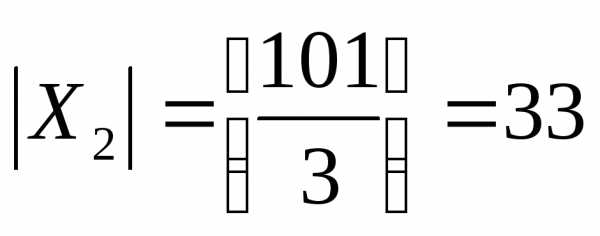 .
.
Тогда множество X1X2 – множество положительных целых чисел, которые делятся и на 2 и на 3. Число элементов или мощность этого множества равно .
Воспользуемся формулой включения и исключения, чтобы найти число элементов множества X.
Получаем
.
studfiles.net
Формула мощности объединения двух множеств A и B — Мегаобучалка
Формула мощности объединения трех множеств A, B и С
Примеры решения
Задание 1
Пусть множество А – это область определения функции
Множество В – это область определения функции
Найти и изобразить на числовой прямой множества
Решение
Функция не определена при . Следовательно,
Функция определена при . Следовательно,
Тогда
Задание 2
Среди 160 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 45 абитуриентов, по физике – 39, по русскому языку – 44, по математике или физике – 78, по математике или русскому языку – 72, по физике и русскому языку – 14, по всем трём предметам – 6.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
Решение
Пусть множество А – абитуриенты, получившие «пятерки» на экзамене по математике, множество В – абитуриенты, получившие отличную оценку на вступительном экзамене по физике, множество С – те, кто сдал на «отлично» русский язык.
U – это универсальное множество, то есть все абитуриенты.
Тогда по условию задачи
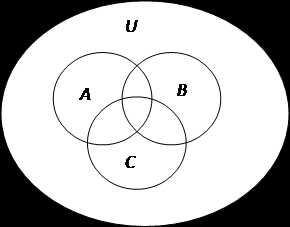
Пусть D – множество абитуриентов, которые получили хотя бы одну пятёрку.
Задания для самостоятельного решения
Задание 1
Пусть множество А – это область определения функции
Множество В – это область определения функции
Найти и изобразить на числовой прямой множества
В задание используются следующие обозначения:
– количество букв в Вашем полном имени;
– количество букв в Вашем отчестве;
– количество букв в Вашей фамилии.
Задание 2
1. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
2. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
3. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике и физике – 10, по математике и русскому языку – 14, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
4. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
5. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
6. Среди 155 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 73, по математике или русскому языку – 72, по физике и русскому языку – 13, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
7. Среди 160 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
8. Среди 155 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 47 абитуриентов, по физике – 36, по русскому языку – 42, по математике или физике – 12, по математике или русскому языку – 76, по физике и русскому языку – 14, по всем трём предметам – 5.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
9. Среди 170 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 52 абитуриента, по физике – 38, по русскому языку – 41, по математике или физике – 75, по математике и русскому языку – 14, по физике или русскому языку – 66, по всем трём предметам – 7.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
10. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.
Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?
Контрольные вопросы
1. Что такое множество?
2. Какие способ задания множества вы знаете?
3. Что такое мощность множества?
4. Какие операции над множествами вы знаете?
5. Напишите формулу мощности объединения четырех множеств и проиллюстрируйте ее диаграммой вена.
megaobuchalka.ru
Лекция 2.Декартово произведение. Мощность множества
2. Декартово произведение. Мощность множества.
2.1. Декартово произведение множеств.
Упорядоченная пара 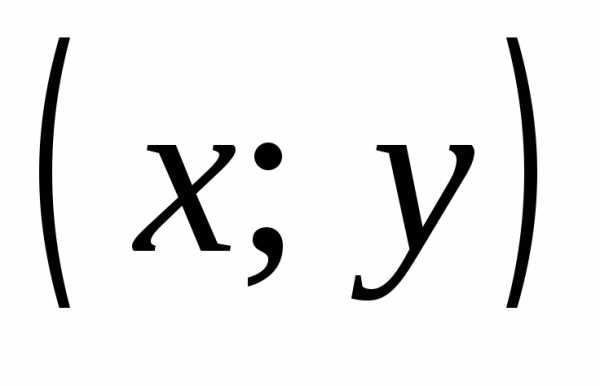 определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары
определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары 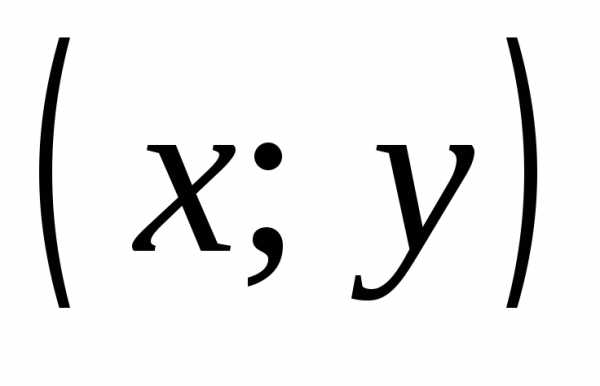 и
и 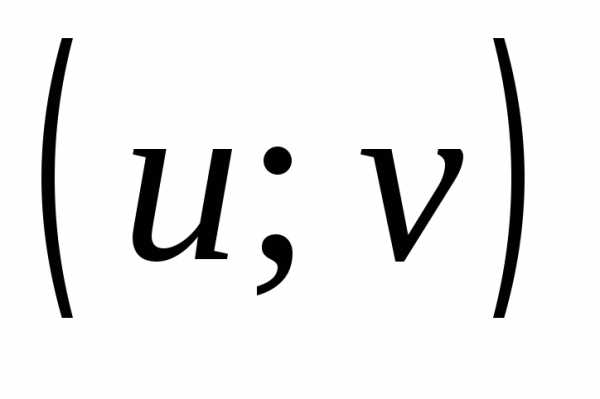 считаются равными тогда и только тогда,
когда x=u и y=v.
считаются равными тогда и только тогда,
когда x=u и y=v.
Определение 2.1. Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество всех упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B:
.
Пример .. Пусть 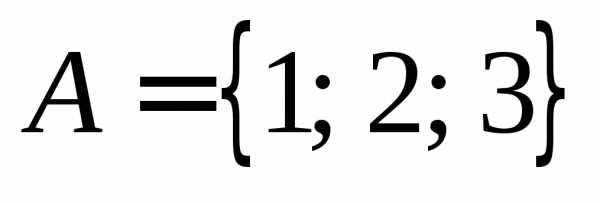 и
и .
Тогда
.
Тогда
.
.

Пример .. На координатной плоскости построить следующее множество:
(-1; 3×1; 3)
Решение. Первое множество помещаем на оси OX, второе на оси OY. Множество всех пар, т.е. декартово произведение, изображается точками заштрихованного прямоугольника, но без левой и нижней стороны.
В общем случае, точка на плоскости может быть задана упорядоченной парой координат, то есть двумя точками на координатных осях. Поэтому координатную плоскость можно задать в виде . Метод координат ввел в употребление Рене Декарт (1596-1650), отсюда и название «декартово произведение».
Диаграмма Венна, иллюстрирующая декартово произведение АхВ
В частности, если A пусто или B пусто, то, по определению, AB пусто.
Понятие прямого произведения допускает обобщение.
Прямое произведение множеств A1, A2, …, An – это множество наборов (кортежей):
.
Множества Ai не обязательно различны.
Степенью множества A называется его прямое произведение самого на себя. Обозначение:
.
Соответственно, и вообще.
Пример .. Пусть B=0, 1. Описать множество Bn.
Решение. Множество Bn состоит из последовательностей нулей и единиц длины n. Они называются строкой бит или битовой строкой длины n.


2.2. Мощность множества.
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если каждому элементу множества A соответствует один и только один элемент множества B и каждому элементу множества B соответствует некоторый элемент множества A. В этом случае говорят также, что множества A и B изоморфны и используют обозначение AB.
Определение 2.2. Два множества A и B называются эквивалентными, или равномощными, если между этими множествами может быть установлено взаимно однозначное соответствие. В этом случае пишут: AB, или A=B, и говорят, что множества A и B имеют равные мощности.
Пример ..
1) Множество десятичных цифр равномощно множеству пальцев на руках человека.
2) Множество четных натуральных чисел (2N) равномощно множеству всех натуральных чисел (N).
Определение 2.3. Множество A называется конечным, если оно эквивалентно Jn при некотором n, где Jn=1, 2, …, n – множество n первых натуральных чисел.
Определение 2.4. Мощностью конечного множества A, которое содержит k элементов, называется число его элементов. Она обозначается A=k. Пустое множество считается конечным с числом элементов равным нулю, т.е. =0.
Таким образом, если множество A конечно, т.е. A=k, то элементы A всегда можно перенумеровать, то есть поставить в соответствие элементам номера из отрезка натурального ряда 1..k с помощью некоторой процедуры. Наличие такое процедуры подразумевается, когда употребляется запись A=a1, a2, …, ak.
Пример .. В компьютере все множества реальных объектов конечны: множество адресуемых ячеек памяти, множество исполнимых программ, множество тактов работы процессора.
Множества, которые не являются конечными, называются бесконечными. Если некоторое множество A равномощно множеству натуральных чисел N, т.е. AN, то множество A называется счетным. Счетное множество A – это такое множество, все элементы которого могут быть занумерованы в бесконечную последовательность a1, a2, …, an, …, так, чтобы при этом каждый элемент получил лишь один номер n и каждое натуральное число n было бы номером лишь одного элемента множества A.
Мощность счетного
множества принято обозначать через 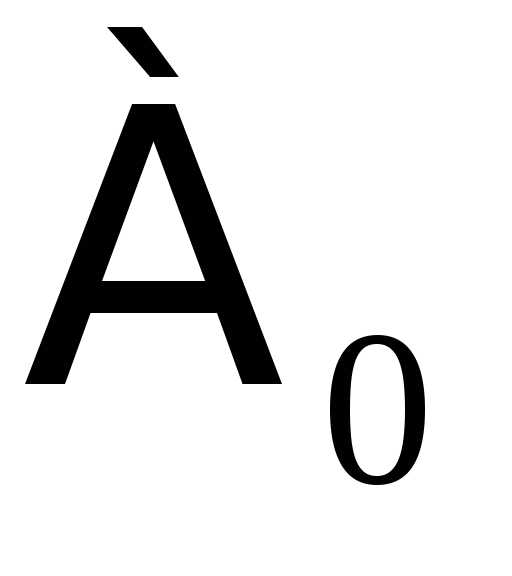 (
( – первая буква древнееврейского
алфавита, называемая «алеф», символ
– первая буква древнееврейского
алфавита, называемая «алеф», символ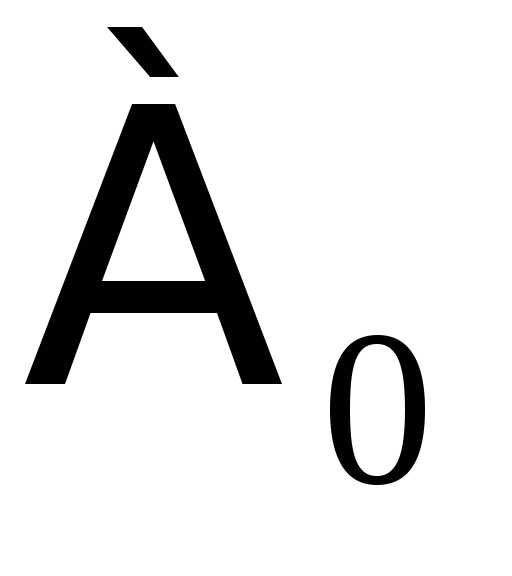 читается: «алеф-нуль»).
читается: «алеф-нуль»).
Наименьшая бесконечная мощность – мощность множества натуральных чисел
N=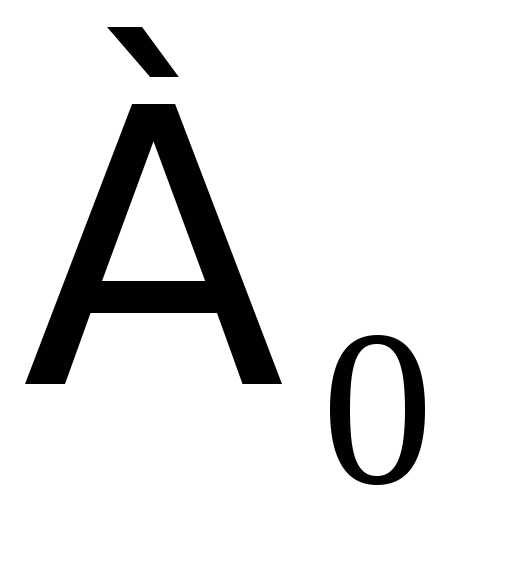 .
.
Пример .7. Множество Z – множество целых чисел также счетно.
Решение. Рассмотрим множество целых чисел Z:
…, n, …, 3, 2, 1, 0, 1, 2, 3, …, n, … .
На первый взгляд, кажется, что это множество невозможно перенумеровать. Однако эту нумерацию можно осуществить, применив следующую хитрость: двигаясь не в одном направлении, а все время менять его.
Иными словами, будем нумеровать так: числу 0 дадим номер 1, числу 1 – номер 2, числу 1 – номер 3, числу 2 – номер 4, числу 2 – номер 5, и т.д. Таким образом, получаем взаимно однозначное соответствие между множеством Z и N. А значит, множество Z счетно.
Множество A называется несчетным,
если его мощность больше мощности
множества N.
В таком случае множество A называется континуальным или континуумом.
Мощность континуума обозначается 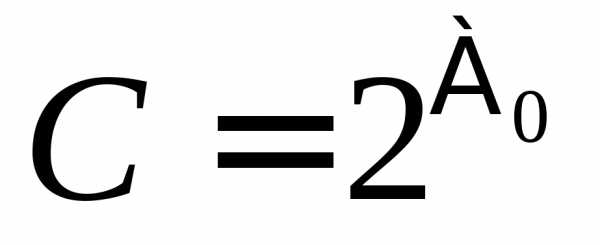 .
Следующую теорему примем без доказательства.
.
Следующую теорему примем без доказательства.
Теорема 2.1. Множество всех действительных чисел имеет мощность континуума, т.е. R=C.
2.3. Теоремы сложения и умножения.
Формула включений и исключений.
Теорема 2.2. (Теорема сложения)
Пусть – конечные попарно непересекающиеся множества, т.е.. Тогда
(2.3.1.)
Доказательство. Докажем теорему методом математической индукции.
Базис индукции. Пусть n=2. Пусть множества X1=A и X2=B, мощности которых соответственно равны k1 и k2, т.е. A=k1, B=k2. Так как AB=, то
.
Индуктивный переход. Пусть теорема верна для n. Покажем, что для n+1 будет тоже справедливо. Тогда
Теорема 2.3. (Теорема умножения)
Пусть заданы конечные множества . Тогда
(2.3.2.)
т.е. число элементов декартова произведения множеств равно произведению количеств элементов сомножителей.
Доказательство. Докажем теорему методом математической индукции.
Базис индукции. Пусть n=2. Пусть множества X1=A и X2=B, мощности которых соответственно равны k1 и k2, т.е. A=k1, B=k2. Первый компонент упорядоченной пары можно выбрать k1 способами, второй – k2 способами. Таким образом, всего имеется k1k2 различных упорядоченных пар. Значит,
.
Индуктивный переход. Утверждение теоремы справедливо для n. Покажем, что оно будет справедливо и для n+1. Имеем:
Пример .. Сколько существует целых чисел между 0 и 1000, содержащих ровно одну цифру 6?
Решение. Пусть S – множество целых чисел между 0 и 1000, содержащих ровно одну цифру 6. Рассмотрим три подмножества S1, S2 и S3 множества S.
S1 – множество, которое содержит число, состоящее из одной цифры, и эта цифра 6;
S2 – множество, содержащее двузначные числа ровно с одной цифрой, равной 6;
S3 – множество, содержащее трехзначные числа ровно с одной цифрой, равной 6.
Множество S1 содержит только один элемент – число 6. Значит, S1=1.
В множестве S2 каждый элемент, содержащей 6, имеет ее либо первой, либо второй цифрой. Если 6 – вторая цифра, то существует 8 различных чисел, которые будут стаять на первом месте, поскольку первое число не может быть 0 или 6. Если 6 – первая цифра, то таких чисел 9, поскольку вторая цифра не может быть 6. Таким образом, S2 содержит 8+9=17 элементов, т.е. S2=17.
Элемент из S3 содержит 6 как первою, вторую или третью цифру.
Если 6 – первая цифра, то существует 9 вариантов выбора второй цифры и 9 вариантов выбора третьей цифры. Согласно комбинаторному принципу умножения, S3 содержит 99=81 чисел с первой цифрой 6.
Если 6 – вторая цифра, то имеются 9 вариантов выбора третьей цифры и 8 вариантов выбора первой цифры, поскольку первая цифра не может быть нулем. Следовательно, S3 содержит 98=72 числа, у которых 6 – вторая цифра.
Аналогично, S3 содержит 72 числа, у которых 6 – третья цифра. Следовательно, всего S3 содержит 81+72+72=225 элементов, т.е. S3=225.
Поскольку и множестваS1, S2 и S3 попарно непересекающиеся, то
.
Поставим задачу подсчитать число элементов в объединении
X=X1X2…Xm
конечных
множеств 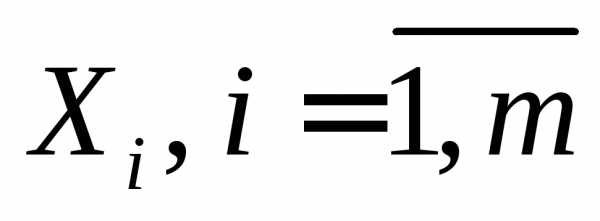 ,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
Теорема 2.4. (Формула включений и исключений).
Для конечных множеств 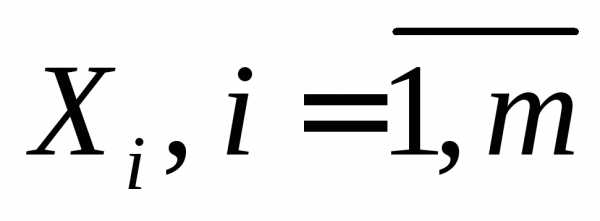 ,
справедлива формулавключений
и исключений.
,
справедлива формулавключений
и исключений.
(2.3.3.)
В частности для двух множеств эта формула примет вид:
.
Для трех множеств формула включений и исключений примет вид:
.
Название этой теоремы подчеркивает использование последовательных включений и исключений элементов подмножеств.
Пример .. Сколько положительных целых чисел, меньших 101, делятся на 2 или на 3?
Решение. Пусть X – множество положительных целых чисел, которые делятся на 2 или 3. Рассмотри два подмножества X1 и X2 множества X.
X1 – множество положительных целых чисел,
которые делятся на 2. Число элементов
или мощность этого множества равно 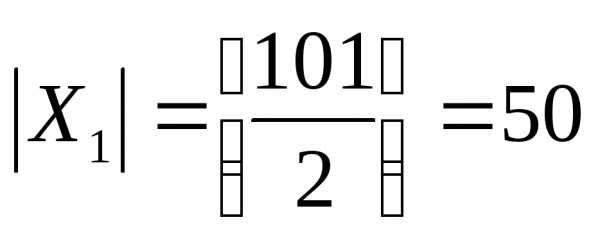 .
.
X2 – множество положительных целых чисел,
которые делятся на 3. Число элементов
или мощность этого множества равно 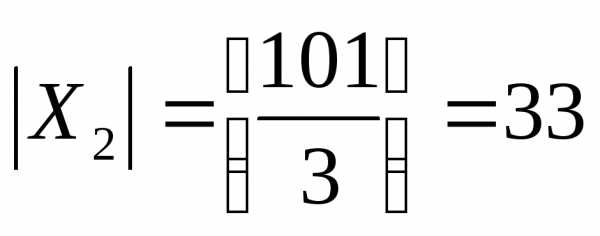 .
.
Тогда множество X1X2 – множество положительных целых чисел, которые делятся и на 2 и на 3. Число элементов или мощность этого множества равно .
Воспользуемся формулой включения и исключения, чтобы найти число элементов множества X.
Получаем
.
studfiles.net
