Постройте матрицу смежности – Матрица смежности

Инцидентность и смежность в графах, матрицы смежности, матрицы инцидентности

Инцидентность — это когда вершина a является либо началом либо концом ребра e. Две вершины называются инцидентными, если у них есть общее ребро.

Для того, чтобы задать граф аналитически, множества V вершин графа и множества U рёбер графа, которые фигурировали в определении графа, будет недостаточно. Потребуется ещё и множество P троек вида (a, u, b), указывающих какую пару a, b элементов множества вершин V соединяет тот или иной элемент u множества рёбер U графа. Элементы множества P называются инциденциями графа. Вот мы и подошли к одному из первых понятий теории графов — инцидентности.

Понятие инцидентности — одно из главных при создании структур данных для представления графов в памяти ЭВМ, к которым мы перейдём после примера 1.

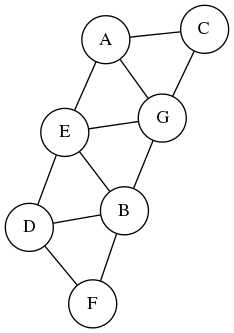
Пример 1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)

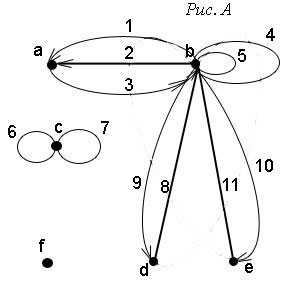
Решение. Распространённые ошибки — не заметить вершины графа, которые не соединены ни с одной другой вершиной, в том числе с самой собой, и не включить их во множество вершин графа, а также указать не все рёбра графа, соединяющие две вершины. Поэтому вершину f данного графа обязательно включаем во множество вершин графа V, а, рёбра 6 и 7, хотя они соединяют одну и ту же вершину саму с собой и обе не имеют направления, включаем во множество рёбер U.

Итак, задаём граф следующими множествами:

множество вершин: V = {a, b, c, d, e, f

}

множество рёбер: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

множество инциденций: P = {(b, 1, a), (b, 2, a), (a, 3, b), (b, 4, b), (b, 5, b), (c, 6, c), (c, 7, c), (b, 8, d), (d, 8, b), (b, 9, d), (b, 10, e), (b, 11, e), (e, 11, b)}

Смежность вершин графа — это когда две вершины графа соединены ребром.

Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте. При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.

В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.

Наиболее часто используются три такие структуры данных — матрица смежности, матрица инцидентности и список инцидентности.

Матрица смежности, как и матрица инцидентности, позволяет установить множество вершин, соседних с заданной (то есть рассматриваемой в конкретной задаче), не прибегая к полному просмотру всей матрицы. Матрицы смежности обычно представляются двумерным массивом размера n x n, где n — число вершин графа.

Матрица смежности S — это квадратная матрица, в которой и число строк, и число столбцов равно n — числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.

Матрица смежности для неориентированного графа

Элемент матрицы смежности sij неориентированного графа определяется следующим образом:

— равен единице, если вершины vi и vj смежны;

— равен нулю, если вершины vi и vj не смежны.

Если для элемента матрицы vij имеет место i = j, то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.

V	1	2	3	4	5
1	0	1	1	0	0
2	1	0	0	1	1
3	1	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.

Матрица смежности для ориентированного графа

Элемент матрицы смежности sij ориентированного графа определяется следующим образом:

— равен единице, если из вершины vi в вершину vj входит дуга;

— равен нулю, если из вершины vi в вершину vj дуга не входит.

Как и для неориентированных графов, так и для ориентированных, если для элемента матрицы vij имеет место i = j, то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 3. Составить матрицу смежности для графа, представленного на рисунке ниже.

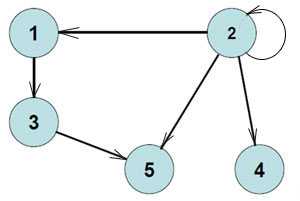
Ответ.

V	1	2	3	4	5
1	0	1	0	0	0
2	0	1	0	0	0
3	1	0	0	0	0
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности ориентированного графа не симметрична.

Матрица смежности для графа с кратными рёбрами

Если в графе есть вершины, соединённые между собой несколькими рёбрами, то элемент матрицы смежности sij равен числу рёбер, соединяющих вершины vi и vj. Из этого следует, что если вершины vi и vj не соединены рёбрами, то элемент матрицы смежности sij равен нулю.

Пример 4. Составить матрицу смежности для графа, представленного на рисунке ниже.

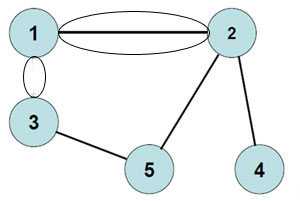
Ответ.

V	1	2	3	4	5
1	0	3	2	0	0
2	3	0	0	1	1
3	2	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Матрица смежности для взвешенного графа

В случае взвешенного графа элемент матрицы смежности sij равен числу w, если существует ребро между вершинами vi и vj с весом w. Элемент sij равен нулю, если рёбер между вершинами vi и vj не существует.

Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.

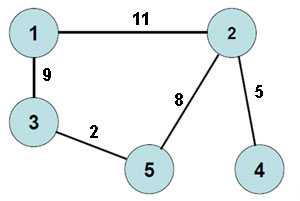
Ответ.

V	1	2	3	4	5
1	0	11	9	0	0
2	11	0	0	5	8
3	9	0	0	0	2
4	0	5	0	0	0
5	0	8	2	0	0

Матрица инцидентности H — это матрица размера n x m, где n — число вершин графа, m — число рёбер графа. Обычно в матрице инцидентности строки соответствуют вершинам графа, а столбцы — рёбрам графа.

Матрица инцидентности для неориентированного графа

Элемент матрицы инцидентности для неориентированного графа hij определяется следующим образом:

— равен единице, если вершина vi инцидентна ребру ej;

— равен нулю, если вершина vi не инцидентна ребру ej.

Пример 6. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.

V	1-2	1-3	2-4	2-5	3-5
1	1	1	0	0	0
2	1	0	1	1	0
3	0	1	0	0	1
4	0	0	1	0	0
5	0	0	0	1	1

Матрица инцидентности для ориентированного графа

Элемент матрицы инцидентности для ориентированного графа hij определяется следующим образом:

— равен минус единице, если вершина vi является началом ребра ej;

— равен единице, если вершина vi является концом ребра ej;

— равен нулю, если вершина vi не инцидентна ребру ej.

Пример 7. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.

V	1-2	1-3	2-4	2-5	3-5
1	1	-1	0	0	0
2	-1	0	-1	-1	0
3	0	1	0	0	-1
4	0	0	1	0	0
5	0	0	0	1	1

На сайте есть пример реализации на языке программирования С++ алгоритма обхода в глубину графа, представленного матрицей инцидентности.

Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.

Список инцидентности одной вершины графа включает номера вершин, смежных с ней.

Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.

Пример 8. Составить списки инцидентности для графа, представленного на рисунке ниже.

Ответ.

1:2→3
2:1→4→5
3:1→5
4:2
5:2→3

Матрицы смежности и инцидентности целесообразнее использовать когда:

• число вершин графа невелико;
• число рёбер графа относительно большое;
• в алгоритме часто требуется проверять, соединены ли между собой две вершины;
• в алгоритме используются фундаментальные понятия теории графов, например, связность графа.

Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.

Списки инцидентности целесообразнее использовать когда:

• число вершин графа велико;
• число рёбер графа относительно невелико;
• граф формируется по какой-либо модели;
• во время действия алгоритма часто требуется модифицировать граф;
• в алгоритме часто используются локальные свойства вершин, например, например, окрестности вершин.

На практике списки чаще используются в прикладных целях.

Весь блок «Теория графов»

function-x.ru

как построить матрицы смежности, инцидентности — 28 Октября 2013 — Примеры решений задач

матрицы смежности, инцидентности

Пусть D = (V, Х) – орграф, где V={v1, v2, …,vn}, X={x1, x2, …, xm}.

Определение. Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой

Определение. Матрицей инцидентности орграфа D называется (nґm) –матрица B(D)=[bij], у которой

Введем также матрицы смежности и инцидентности для неориентированных графов. Пусть G = (V, X) – граф, где V={v1, v2, …,vn}, X={x1, x2, …, xm}.

Определение. Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой

Определение. Матрицей инцидентности графа G называется (nґm) –матрица B(G)=[bij], у которой

С помощью введенных матриц удобно задавать графы для обработки на ЭВМ. Используя матрицу смежности легко определить локальные степени вершин графа: сумма элементов матрицы по строке равна локальной степени соответствующей вершины. Для орграфов по строке определяются полустепени исхода, по столбцам – полустепени захода.

Пример 72.

Построить матрицы смежности и инцидентности для графа G = (V, X) (рис. 25).

Решение.

Матрица смежности имеет вид

.

Поскольку граф не имеет петель, то на главной диагонали стоят все нули. Для любого графа матрица смежности симметрична относительно главной диагонали.

Для того, чтобы построить матрицу инцидентности необходимо пронумеровать ребра графа (рис. 26). Матрица инцидентности имеет вид:

Напомним, что в строках указываются вершины, в столбцах – ребра. Матрица инцидентности может быть как квадратной, так и прямоугольной.

Пример 73.

Построить матрицы смежности и инцидентности для  орграфа D= (V, X) (рис. 27).

Решение.

Матрица смежности имеет вид:

Матрица инцидентности имеет вид

www.reshim.su

Построить граф по матрице

Построить ненаправленный граф по матрице

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г.

Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками.

Однако дальнейшее развитие математики и особенно ее приложений дало сильный толчок развитию теории графов.

Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем.

Граф — это  одно из представлений  связей, между объектами / событиями.

В настоящее время теория графов находит многочисленные применения в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сеги нефтепроводов и вообще в так называемом «программировании». Теория графов теперь применяется и в таких областях, как экономика, психология и биология. 

В виде графов преобразовываются электрические схемы,  производственные цепочки на предприятии, план мероприятий, оптимальная логистическая доставка, связи между родственниками, друзьями  и многое другое.

Графы делятся на ненаправленные, направленные, с весовыми коэффицикентами(взвешенные) и без коэффициентов.

Каждый граф имеет определенные характеристики. Основные из них это остов графа, матрица смежности, матрица инцидентности.

Остов графа — это подграф данного графа, содержащий все его вершины и являющийся деревом.

Матрица смежности графа — это квадратная матрица ( по числу вершин графа) где, каждый элемент матрицы (на пересечении i- столбца и j-ряда) есть состояния связи  между вершинами i и j.

Элемент матрицы равен 1 если i-вершина графа, соединена с j-вершиной графа.

Во всех других случаях, в том числе когда i=j, значение элемента матрицы равно 0.

Это условие применимно только для ненаправленных графов и только для связей которые не начинаются и заканчиваются на одной и той же вершине ( петля)

Ненаправленный граф — граф, где не указаны направления движения связей между любыми  вершинами.

Невзвешенный граф — граф, где связям между любыми вершинами не присвоено никакое значение, а показывает только лишь сам факт связи этих двух вершин

На этой странице  бот строит ненаправленный граф, если  для него задана  матрица смежности.

Если мы не можете в уме построить матрицу смежности, то для этого есть ресурс Теория графов. Матрица смежности онлайн где можно построить такую матрицу. 

Интересные особенности

В матрице смежности неориентированного графа (взвешенного или невзвешенного) не важно, есть одна очень важная особенность

Значения матрицы  относительно главной диагонали — одинаковы.

Таким образом в принципе достаточно в качестве исходных данных вводить только верхнюю(диагональную) часть матрицы, но для удобства восприятия, ввод данных был сделан для полной матрицы.

Второй вывод который следует из вышесказанного следующий( и в примерах он прослеживается): Бот не проверяет  симметричность-соответствие  данных  в позициях матрицы относительно главной диагонали. 

Примеры:

Задана матрица смежности такого вида

 

В запросе пишем  0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0

и получаем ответ

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

---

Матрица задана таким видом

Пишем в запросе 

0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 1 0 0 0  0 1 0  0 0 1 0 1 0 0 1 0 1 0 1 0 0 0 0 0  1 0 0 0 0 1 0 0 0 1 0 0

получем ответ

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

 

Удачи в расчетах!!

 

• Построить график функции c помощью GeoGebra >>

abakbot.ru

Построение геометрических орграфов на основании матриц

Отношение x > y обладает следующими свойствами:

1. Оно антирефлексивно, так как ни для каких х не имеет места x > x,  орграф отношения не имеет петель.
2. Оно асимметрично, так как для двух чисел имеет место только соотношение x > y.
3. Оно транзитивно, так как если x > y и y > z, то x > z, орграф отношения  является транзитивным, т.е. существуют замыкающие дуги:  и  влечет  и т.д.

Пример 5. Задана матрица

Нарисовать на плоскости орграф G = ( X, U ), единственный с точностью до изоморфизма, имеющий заданную матрицу В своей матрицей смежности. Найти матрицу инцидентности   орграфа G.

Решение. Заданная матрица смежности В имеет 4 строки и 4 столбца, следовательно, орграф имеет 4 вершины. Обозначим их соответственно ,, , . Матрицу В перепишем в виде

.

Построим на плоскости 4 точки и обозначим их ,, , .

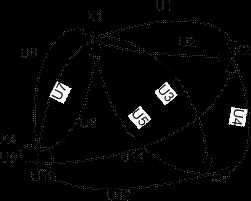
Рис. 22. Изоморфный орграф G = ( X, U ).

Так как , то при вершине  нет петель, , значит из вершины  исходят 2 стрелки к вершине . Рассуждая таким же образом, построим геометрический орграф, изоморфный орграфу G = ( X, U ), для которого матрица В является матрицей смежности ( рис. 22 ).

Теперь запишем матрицу инцидентности С для орграфа G.

Построенный орграф G = ( X, U ) имеет 4 вершины и 12 дуг, т.е. Х={,,,},

U= .

Матрица инцидентности орграфа G будет иметь 4 строки и 12 столбцов

 Петле соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в орграфе, но не указывает, каким вершинам эти петли инцидентны.

3. Задана симметрическая матрица А неотрицательных целых чисел.

    1. Нарисовать на плоскости граф (единственный с точностью до изоморфа), имеющий заданную матрицу А своей матрицей смежности. Найти матрицу инцидентности  графа G.

     2. Нарисовать на плоскости орграф  (единственный с точностью до изоморфизма), имеющий заданную матрицу А свое матрицей смежности. Найти матрицу инцидентности  орграфа G.

А=

            Решение1. Напомним, что матрицей смежности графа  с множеством вершин  называется матрица  размера , в которой элемент  равен числу ребер в G, соединяющих  с . Матрица смежности графа G является симметрической, то есть

=.

            Построим граф  по заданной матрице смежности.

            Поскольку данная матрица является  симметрической матрицей четвертого порядка с неотрицательными элементами, то ей соответствует неориентированный граф с четырьмя вершинами. Расположив вершины  на плоскости произвольным образом  (рис. 3), соединяем их с учетом кратности ребер.

А=

Рис. 3 Граф G=(X,U)

            Теперь найдем матрицу инцидентности графа G =(X,U).

Напомним определение матрицы инцидентности графа G=(X,U) с множеством вершин  и множеством ребер  Так называется матрица  размера , у которой

2. Заданная матрица А имеет 4 строки и 4 столбца, следовательно орграф имеет 4 вершины. Обозначим их соответственно   а матрицу представим в виде

 

            На плоскости строим 4 точки. Обозначим их через

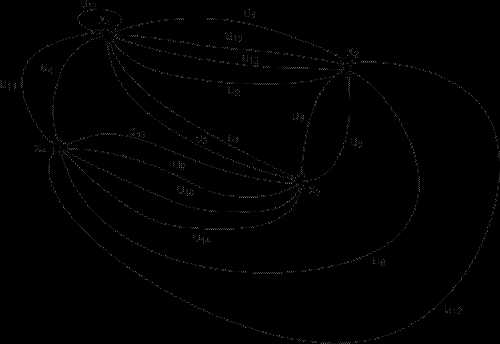
                                                      Рис. 4. Изоморфный орграф G=(X,U).

            Так как   то при вершине   имеется петля;  значит, из вершины  выходят две стрелки к вершине  и т.д. (рис.4).

            Теперь запишем матрицу инцидентности С для орграфа G.

            Построим орграф G=(X,U) имеет 4 вершины и 17 дуг, т.е.

            Матрица инцидентности орграфа G будет иметь 4 строки и 17 столбцов

4. Заданная формула  От формулы  перейти к  эквивалентной ей формуле  так, чтобы формула  не содержала связок «» и «». Исходя из истинностных таблиц, доказать, что формулы  и  равно сильны (логически эквивалентны). Для формулы  СКНФ и СДНФ.

Решение. Как известно, все формулы логики высказываний можно записать при помощи пропозициональных связок :  т.е. пропозициональные связки   могут быть определены в терминах  связок  Можно доказать, что

                                                   (1)

                                                         (2)

                                  (3)

               Используя равенства (1) – (3) и основные законы

21 – 30. Задана симметрическая матрица A неотрицательных целых чисел.

1. Нарисовать на плоскости граф G=(X,U)  (единственный с точностью до изоморфизма), имеющий заданную матрицу А своей матрицей смежности. Найти матрицу инцидентности  

графа G.

2. Нарисовать на плоскости орграф G=(X,U)  (единственный с точностью до изоморфизма)? Имеющий заданную матрицу А своей матрицей смежности. Найти матриц инцидентности

Орграфа G.

21.                                      22.

23.                                 24.         

25.                                        26.

27.                                                28.

29.                                                30.

vunivere.ru

Матрица инцидентности и матрица смежности

На рис. 1,2 изображено множество точек и множество линий , соединяющих эти точки, которые все вместе образуют граф .Если линии имеют стрелки, то граф называется ориентированным или орграфом 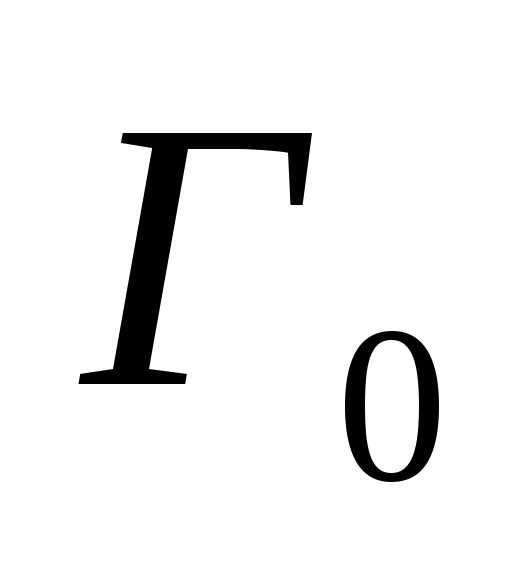(рис. 2).

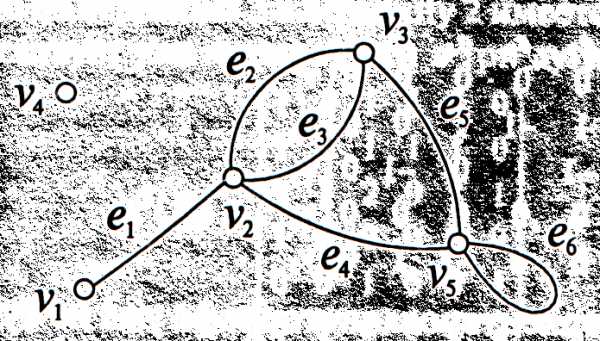
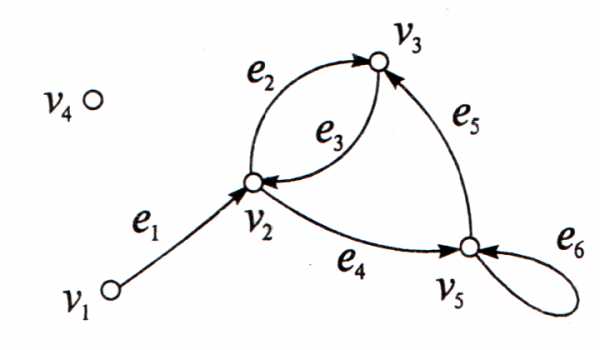
Рис. 1. Граф 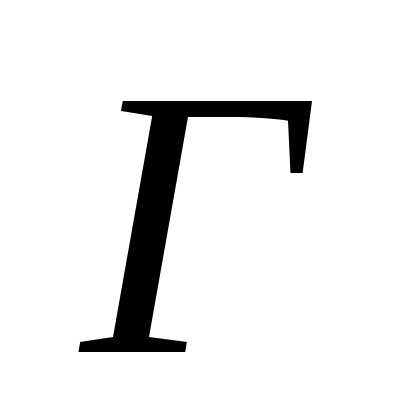. Рис. 2. Орграф .

Графы и можно представить в аналитической форме либо матрицей смежности ,либо матрицей инцидентности .

Для нашего конкретного неориентированного графа матрицы и выглядят следующим образом:

Матрица смежности для неориентированного графа всегда симметрична.

Фигурирующая в ней 2 может быть в некоторых случаях заменена на 1.

В матрице инцидентности сумма единиц по столбцам указывает на степень вершины v_i. Нередко расположение вершин и ребер в этой матрице меняют местами (транспонируют). Так, для нашего конкретного орграфа матрицы и выглядят существенно иначе:

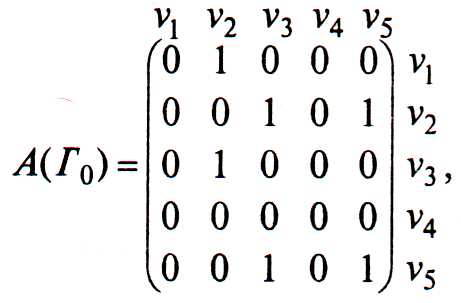
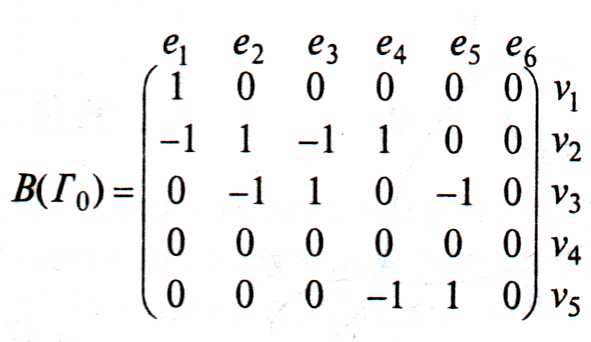
В общем случае матрица смежности для ориентированного графа 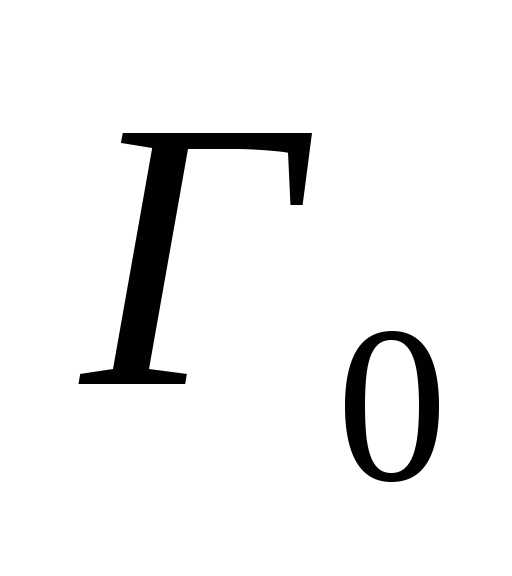уже не будет симметричной. В матрице инцидентности ставится 1, если дуга исходит из вершины, и —1, если дуга заходит в нее.

Матрица смежности и матрица инцидентности

Есть два стандартных способа представить граф G = (V,E) 

Первый обычно предпочтительнее, ибо дает более компактное представление разреженных графов– тех, у которых |E| много меньше |V|².

Большинство стандартных алгоритмов используют именно это представление. Но в некоторых ситуациях удобнее пользоваться матрицей смежности – например, для плотных графов, у которых |EG| сравнимо с |VG|².

Матрица смежности позволяет быстро определить, соединены ли две данные вершины ребром. Алгоритмы отыскания кратчайших путей для всех пар вершин, используют представление графа с помощью матрицы смежности.

• Определение Матрицей смежностиграфа G = (V, E) называется квадратная булева матрицаAпорядкаn,элементы которой определяются следующим образом:

Свойства

1. А – симметрическая матрица

2. На главной диагонали матрицы смежности всегда стоят 0.

3. Число единиц в строке равно степени соответствующей вершины.

Матрицей инцидентностиграфаGназывается булева матрица размера |V|´|G| вида

Свойства:

1.   В каждом столбце матрицы ровно две единицы

2. Равных столбцов нет.

Например, на следующем рисунке граф задан графически, списком смежных вершин, матрицей смежности и матрицей инцидентности.

графически	список смежных вершин     номер вершины степень вершины         1 2 2 5     2 4 1 3 4 5 3 2 2 4     4 3 2 3 5   5 3 1 2 4
матрица смежности   1 2 3 4 5 1 0 1 0 0 1 2 1 0 1 1 1 3 0 1 0 1 0 4 0 1 1 0 1 5 1 1 0 1 0	матрица инцидентности   e1 e2 e3 e4 e5 e6 e7 1 1 1 0 0 0 0 0 2 0 1 1 0 1 1 0 3 0 0 0 0 0 1 1 4 0 0 0 1 1 0 1 5 1 0 1 1 0 0 0

Рассматриваются также графы с нагруженными ребрами или взвешенные – графы, у которых каждому ребру поставлено в соответствие некоторое вещественное число – вес или нагрузка ребра.

Такой граф можно задать матрицей расстояний – квадратной матрицей размера |V|´|V|, где на пересечении i-ой строки и j-го столбца записан вес ребра (i, j), если ребро есть, ¥, если ребра нет и 0, если i = j.

studfiles.net

Пусть G – помеченный граф порядка N , V(G) = {1, 2, 3, …, N}. Матрицей смежности графа G называется бинарная N´N-матрица M(G) = (Mij), такая, что Mij = 1, если вершина I смежна с вершиной J, и Mij = 0, в противном случае.

Легко видеть, что матрица смежности простого графа G является симметричной, с нулями на главной диагонали. Число единиц в каждой строке (каждом столбце) равно степени соответствующей вершины. Понятно, что и обратно, всякой бинарной матрице с указанными свойствами соответствует некоторый простой граф. Таким образом, матрица смежности является одним из способов задания графов.

Для мульти — и псевдографов матрица смежности определяется так, что:

Mij =

Для ориентированного графа G:

Mij =

Таким образом, всякая бинарная матрица является матрицей смежности соответствующего ориентированного графа. Например, следующей матрице соответствует изображенный далее граф.

Абстрактный граф приводит к различным матрицам смежности в зависимости от нумерации вершин.

Теорема. Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга путём парных перестановок одинаковых строк и столбцов.

Доказательство. Действительно таким перестановкам (переставляются одновременно, как одна операция, две строчки и два столбца с одинаковыми номерами) соответствует перенумерация вершин графа, что очевидно приводит к изоморфному графу.

Из теоремы, в частности, следует, что ранги матриц смежности изоморфных графов совпадают. Этот общий ранг различных матриц смежности изоморфных графов называется рангом соответствующего абстрактного графа G и обозначается rg G. Совпадают так же характеристические многочлены и собственные значения матриц смежности изоморфных графов, которые называются, соответственно, характеристическим многочленом и спектром графа G.

Для двудольного графа G, с долями V1 = {X1, X2, …, Xn} и V2 = {Y1, Y2, …, Ym} рассматривается так же приведённая N´M-матрица смежности, такая, что Mij = 1, если вершина Xi смежная с Yj, и Mij = 0 в противном случае.

Для взвешенных графов вместо матрицы смежности обычно рассматривается матрица весов, элементы которой mij = вес рёбра {i, j}. Отсутствующим рёбрам присваивается вес ∞ или 0, в зависимости от решаемой задачи.

< Предыдущая		Следующая >

matica.org.ua