Решение кубических уравнений – .

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы.

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы.

Кубическим уравнением называется уравнение вида

ax³ + bx² + cx +d = 0 , (1)

где a, b,c ,d — постоянные коэффициенты, а х — переменная.

Мы рассмотрим случай, когда коэффициенты являются веществеными числами.

Корни кубического уравнения.

Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.

Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:

Δ= -4b³d

+ b²c² — 4ac³ + 18abcd — 27a²d².

Итак, возможны только 3 следующих случая:

• Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
• Δ < 0 — уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
• Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)

На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.

Формула Кардано.

Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).

Канонической формой кубического уравнения называется уравнение вида

y³ + py + q = 0 (2)

К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:

x= y — b/3a (3)

p= — b²/3a² + c/a

q= 2b³/27a³ — bc/3a² + d/a

Итак, приступим к вычислению корней. Найдем следующие величины:

Q=(p/3)³ + (q/2)²

α = (-q/2 + Q^1/2)^1/3

β = (-q/2 — Q^1/2)^1/3

Дискриминант уравнения (2) в этом случае равен

Δ = — 108Q

Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:

y₁= α + β

y₂= — (α + β)/2 + (3^1/2(α — β)/2)i

y₃ =- (α + β)/2 — (3^1/2(α — β)/2)i

Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y₁. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y₂, y₃ и подставьте их в (3).

Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y

1, y₂, y₃ и подставьте их в (3).

Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем

α = β, и

y₁=2α,

y₂= y₃ = — α. Аналогично подставляем в (3) и получаем ответ.

Тригонометрическая формула Виета.

Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида

x³ + ax² + bx +c = 0 (4)

Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.

Итак, алгоритм применения этой формулы:

1. Вычисляем

Q=(a²— 3b)/9

R=(2a³ — 9ab + 27c)/54

2. Вычисляем

S = Q³ — R²

3. a) Если S>0, то вычисляем

φ=(arccos(R/Q^3/2))/3

И наше уравнение имеет 3 корня (вещественных):

x₁= — 2(Q)^1/2cos(φ) — a/3

x₂= — 2(Q)^1/2cos(φ+2π/3) — a/3

x₃= — 2(Q)^1/2cos(φ-2π/3) — a/3

б) Если S<0, то заменим тригонометрические функции гиперболическими.

Вычисляем

φ=(Arch( |R|/|Q|^3/2)/3

Тогда

единственный корень (вещественный): x₁= -2sgn(R)*|Q|^1/2*ch(φ) — a/3

Для тех, кого интересуют также и мнимые корни:

x₂= sgn(R)*|Q|^1/2*ch(φ) — a/3 +(3|Q|)^1/2 sh(φ)i

x₃= sgn(R)*|Q|^1/2*ch(φ) — a/3 -(3|Q|)^1/2sh(φ)i

 

ГДЕ:

ch(x)=(e^x+e^-x)/2

Arch(x) = ln(x + (x²-1)^1/2)

sh(x)=(e^x-e^-x)/2

sgn(x) — знак х

в) Если S=0,то уравнение имеет меньше трех различных решений:

x₁= -2*R^1/3 — a/3

x₂=x₃=R^1/3 — a/3

Оценка статьи:

e4-cem.ru

О решении неполного кубического уравнения / Habr

Intro

Я публикую этот топик как обучающий. Собственно говоря, существенной новизны в материале нет, тема заезжена. Думаю, что интересным будет подход к решению задачи.

Помню, на первом курсе на занятиях по математическому анализу пришел в голову один интеграл. Преподаватель вызвал к доске, но прозвенел звонок. По дороге домой в автобусе сложился «скелет» решения кубического уравнения. Общая схема, конечно, не самая рациональная. Есть более эффективная — тригонометрическая формула Виета. Там сразу выписывается корень по виду уравнения, а, вообще, по объему вычислений все-таки лучше использовать численный метод Ньютона, поскольку степенные ряды для обратных тригонометрических функций сходятся медленно (по ним строятся вычисления таких функций в некоторых библиотеках). Вот что получилось.

1. Исходный интеграл и кубическое уравнение

Нужно найти неопределенный интеграл

Применяя метод неопределенных коэффициентов, представим знаменатель подынтегральной функции как

откуда получаем нелинейную систему алгебраических уравнений относительно неизвестных коэффициентов, для решения которой требуется найти положительный корень неполного кубического уравнения

Исследуя функцию в левой части уравнения на монотонность, можно выяснить, что она имеет максимум

и минимум

При этом

Тогда из непрерывности функции следует, что исходное уравнение имеет три действительных корня, причем два отрицательных и один положительный, принадлежащий отрезку , .
Найдем его.

2. Поиск положительного решения

Заметим, что наше уравнение не имеет рациональных корней.
Начнем со следующего тождества, справедливость которого, наверное, многие доказывали в школе:

Преобразуем его к виду

Тогда решение кубического уравнения сводится к решению системы

причем (по условию положительности корня).
От данной системы перейдем к системе

По сути в (1) записана теорема Виета для квадратного уравнения

или

Дискриминант здесь отрицательный, казалось бы, можно закончить решение, но нам требуется не действительность и , а действительность их суммы. В этом помогут комплексные числа.

Тригонометрическая форма записи корней квадратного уравнения имеет вид

,
где — мнимая единица.

Тогда

Может возникнуть вопрос: в системе (1) первое уравнение было получено возведением обеих частей в куб, не вызовет ли это появление дополнительных комплексных корней? Нет, поскольку если выразить через в исходной системе, то получится уже рассмотренное квадратное уравнение. При выражении через имеем тоже самое. Это и доказывает справедливость последней совокупности.
Извлечем кубический корень из и по правилу извлечения корней из комплексных чисел. Получим

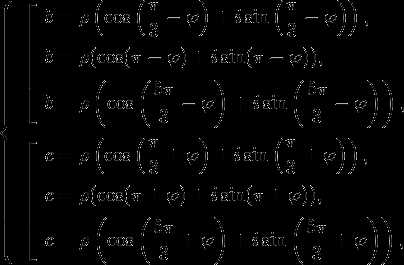
где

Выберем такую пару и , чтобы их сумма в мнимой части комплексного числа давала 0, а действительная часть была бы отрицательной. При этом будем использовать формулы приведения (если требуется найти остальные корни уравнения, то лучше использовать формулы преобразования суммы тригонометрических функций в произведение), а также учтем, что угол принадлежит первой четверти. Тогда

Откуда искомый корень

Если использовать тригонометрическую формулу Виета, то полученный корень запишется в более простой форме

Возникает вопрос: почему я не использовал формулу Кардано? Ведь в школах нам говорили, что для решения кубических уравнений используют ее. По своей форме она похожа на то, что сейчас проделал — в итоге придется извлекать кубический корень из комплексного числа. Кстати, именно при решении уравнений третьей степени комплексные числа впервые получили свое применение.

Замечу, что для выяснения состава корней кубического уравнения используют понятие дискриминанта (как и в случае квадратного уравнения). Вообще, понятие дискриминанта в алгебре введено для многочленов произвольной степени.

2. Пример физической задачи с кубическим уравнением

В журнале «Квант» мне как-то раз попалась интересная задачка по физике с выходом на решение кубического уравнения. Суть в следующем. Нужно определить, какую максимальную скорость может развить автомобиль массой (вместе с человеком) при известной наибольшей мощности двигателя?
При наибольшей скорости автомобиля его ускорение равно нулю, поскольку производная функции обращается в ноль в точке экстремума. Хотя оно равно нулю и при движении с постоянной скоростью. Тогда можно сказать так: какую максимальную постоянную скорость автомобиль может развить?
На больших скоростях пренебрегать сопротивлением воздуха уже нельзя, при этом сила лобового сопротивления выражается не по закону Стокса, а по квадратичному закону, поскольку скорость движения достаточно велика. Тогда сила тяги двигателя уравновешивается силой сопротивления воздуха и силами трения качения и скольжения, возникающими между шиной колеса автомобиля и дорожным полотном:

где — суммарный коэффициент трения, — ускорение свободного падения, — коэффициент аэродинамического сопротивления, — площадь лобового сечения автомобиля, откуда и получаем неполное кубическое уравнение.

3. Вопросы и ответы

При прочтении топика у читателя могли возникнуть вопросы. Например, такие:

1. Почему автор не рассматривал полного кубического уравнения? Ответ: полное кубическое уравнение сводится к неполному заменой

где — новая переменная, — коэффициент при , — коэффициент при .

2. В начале топика был рассмотрен многочлен четвертой степени. Есть ли методы, позволяющие аналитически разрешать такие уравнения? Ответ: да, существует метод Феррари.

3. По теореме Абеля-Руффини уравнение, выше четвертой степени, не разрешимо в радикалах. А тут получается корень кубического уравнения, содержащий тригонометрические функции, который, скорее всего, нельзя выразить через радикалы, как так? Ответ: в формулировке теоремы имеется в виду общая запись корня, т.е. корни могут извлекаться и из комплексных чисел при подстановке в формулы коэффициентов уравнения.

4. После Эвариста Галуа были ли попытки получения формул корней уравнения произвольной степени? Ответ: не так давно мне попался на глаза русский перевод книги американского математика Дэвида Мамфорда «Лекции о тэта-функциях» (Мир, 1988). Там в качестве добавления приведена работа Хироси Умемура «Решение алгебраических уравнений с помощью тэта-констант», где заменяется функция извлечения корня другой функцией — модулярной функцией Зигеля, выражаемой через тэта-константы. В этой работе также освещена история исследования данного вопроса после Галуа.

5. Как я понимаю, такие формулы не применимы для использования в практических задачах решения уравнений произвольной степени. Есть ли какие-нибудь современные работы с описанием алгоритмов получения приближенных корней? Ответ: советую книгу Г.П. Кутищева «Решение алгебраических уравнений произвольной степени: Теория, методы, алгоритмы» (URSS, 2010).

6. Существуют ли современные модификации численного метода Ньютона, являющегося на сегодняшний день основным для получения приближенных решений уравнений и систем уравнений? Ответ: можно посмотреть статью Janak Raj Sharma, Rangan Kumar Guha и Rajni Sharma «An efficient fourth order weighted-Newton method for systems of nonlinear equations».

7. Имеются ли какие-нибудь частные случаи уравнений высокой степени, для которых удалось получить аналитические формулы корней? Ответ: корень Бринга для поиска действительного решения уравнения пятой степени и формула Лоуренса Глассера для неполных уравнений произвольной степени.

В заключении для начинающих рекомендую книгу С.Л. Табачникова и Д.Б. Фукса «Математический дивертисмент» (МЦНМО, 2010).

habr.com

Решение кубического уравнения онлайн | umath.ru

Число знаков после запятой:

Кубическим уравнением называется уравнение вида Если коэффициент то уравнение не является кубическим. Если коэффициент то уравнение имеет корень равный нулю и делением на сводится к квадратному уравнению.

Кубическое уравнение может иметь как действительные, так и комплексные корни. Для обозначения комплексной единицы в ответе калькулятор использует символ .

Дискриминант кубического уравнения показывает природу корней:

• если то уравнение имеет только один действительный корень,
• если то все корни уравнения — действительные,
• если то все корни уравнения действительные и равны между собой.

Для решения уравнения в калькуляторе введите коэффициенты уравнения. Для отрицательных коэффициентов используйте знак -.

Десятичные дроби разделяйте точкой. То есть если какой-то коэффициент равен 1,25, то вводить нужно 1.25.

umath.ru

📝Решение квадратного и кубического уравнения онлайн

Ознакомиться с правилами решения такого упражнения вы можете, пересмотрев формулы. В полях с единицами укажите, ваши коэффициенты при неизвестных.
Квадратное уравнение имеет вид: $ax^2+bx+c=0 $, где $a$ не может быть ровно нулю!

Решение кубического уравнения, которое имеет вид: $ax^3+bx^2+cx+d=0$, где $a$ не может быть ровно нулю!

Решить уравнение – это означает найти такое число, которое могло б заменить неизвестное, и при этом равность выполнялась, то есть была бы правильной. И, не важно, квадратное оно, кубическое или высшей степени, суть одна, разница только в методах нахождение его неизвестного или так називаемого корня.

На вашем конкретном примере онлайн калькулятор все распишет максимально детально. Я только остановлюсь на нескольких основных аспектах. Для первого, метод базируется на нахождении дискриминанта, если он положительных, то существует два разных вещественных корня, если отрицательный, то два комплексных (или нет корней, когда рассматриваются только поле вещественных чисел). Для второго, все значительно сложнее и разных вариантов там на много больше, так что, либо подставляйте в формы выше свои данные или идите на страницу с теорией по данному вопросу.

Так что данный калькулятор поможет вам онлайн найти решение квадратного или кубического уравнения, при этом вы получите подробнейший ход всего решения со всем необходимым теоретическим материалом. С его помощью вы можете, как просто узнать правильный ответ, для проверки самого себя, так и весь метод от начала и до конца, что значительно упростит нахождения ошибки, если она существует. И даже он можете вас научить делать подобные упражнения, если у вас есть желание для этого.

И, конечно же, очень прошу вас изучить страницу Часто задаваемых вопросов и ответов на них, чтобы не повторять ошибки своих предшественников, особенно это нужно для тех, кто собирается задать вопрос в комментариях.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Занятие 17. Трехчленные кубические уравнения

Занятие 17.

Трехчленные кубические уравнения

Рассмотрим один из методов решения неполных кубических уравнений на частных примерах.

Пример 1. Решите уравнение .

Решение

Положим и подставим в уравнение, получим:

или

.

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -16, а произведение 64.

Получим уравнение: , ;

.

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид: .

Получим еще один корень: .Ответ: .

Пример2. Решите уравнение .

Решение

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -4, а произведение 8.

Получим уравнение: , ;

Квадратное уравнение корней не имеет.

Однако, первоначальное кубическое уравнение имеет действительные корни. В самом деле, среди делителей свободного члена: нетрудно найти корень: . В самом деле: .

Разделим, по схеме Горнера, трёхчлен на x — 2, получим:

Уравнение примет вид: . Решим квадратное уравнение:

.

Ответ: .
Пример3. Решите уравнение .
Решение

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -2, а произведение -8.

Получим уравнение: , ;

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид:.

Уравнение не имеет действительных корней, т. к. его дискриминант отрицателен:

.

Уравнение имеет один действительный корень: .

Ответ: .
Не всегда этот метод может дать положительный результат!
Пример 4. Решите уравнение .

Решение

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -30, а произведение .

Получим уравнение: ,

, а значит квадратное уравнение не имеет решений.

Однако, исходное уравнение имеет три действительных корня 2, 3 и -5.

Методика решения такого типа уравнений рассматривается на множестве комплексных чисел и будет приведено ниже.
Задания для самостоятельной работы.

Решите уравнения:

1. . 2. . 3. .

Занятие 18.

Полные кубические уравнения

Полное кубическое (кубичное) уравнение вида

легко приводится к трёхчленному кубическому уравнению подстановкой .

Покажем это

,

,

. Положим , получим трёхчленное кубическое уравнение .
Пример 1. Решите уравнение .

Решение

Положим , получим ,

.

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна 9, а произведение 8.

Получим уравнение: , ;

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид: . Уравнение не имеет действительных корней.

Получим один корень: . Найдем решение данного кубического уравнения: . Оно также имеет один действительный корень.
Ответ: .
Пример 2. Решите уравнение .
Решение
Положим , получим ,

.

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем:

.

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -6 а произведение 8.

Получим уравнение: , ;

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид: .

Уравнение не имеет действительных корней, поскольку его дискриминант отрицателен.

Получим один корень: . Найдем решение данного кубического уравнения: . Оно также имеет один действительный корень.

Ответ: .
Пример 3. Решите уравнение .

Решение

Положим , получим ,

.

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем: .

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна -4 а произведение 8.

Получим уравнение: . Полученное квадратное уравнение не имеет корней на множестве действительных чисел, значит такой метод к решению данного уравнения не применим.

Хотя, совершенно очевидно, что x = 1 является корнем данного уравнения, ибо сумма его коэффициентов равна нулю.

Разделим многочлен на x — 1 по схеме Горнера:

Получаем следующее уравнение: .

Квадратное уравнение имеет два корня:

, .
Ответ: , , .
Пример 4. Решите уравнение .
Решение
Положим , получим ,

.

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем: .

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна 98 а произведение -3375.

Получим уравнение . Оно имеет корни .

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид: . Уравнение не имеет действительных корней.

Получим один корень: . Найдем решение данного кубического уравнения: . Оно также имеет один действительный корень.
Ответ: .
Пример 5. Решите уравнение .
Решение
Преобразуем уравнение, разделив обе его части на коэффициент при , т. е. на 27, получим уравнение: .

Положим , получим ,

,

, .

Положим и подставим в уравнение, получим:

или .

Поскольку и выбраны произвольно, потребуем, чтобы , и поэтому получаем: .

С другой стороны, из равенства находим:

.

Рассмотрим и , как корни квадратного уравнения, сумма корней которого равна а произведение .

Получим уравнение или

Оно имеет корни .

Тогда .

После того, как найден один из действительных корней, следует проверить, а не существуют ли другие действительные корни.

Для этого, применяя теорему Безу, устанавливаем, что кубический трёхчлен будет нацело делится на двучлен . Выполним деление по схеме Горнера:

Уравнение примет вид: .

Уравнение имеет два равных действительных корня .

Получим корни: , . Найдем решение данного кубического уравнения: , , .
Ответ: , .

Задание для самостоятельной работы.

Решите уравнение.

1. ; 2. ; 3. ;

voeto.ru