Правило сложения положительных и отрицательных чисел – .

Сложение и вычитание положительных и отрицательных чисел

Правило сложения отрицательных чисел

Если вспомнить урок математики и тему «Сложение и вычитание чисел с разными знаками», то для сложения двух отрицательных чисел необходимо:

• выполнить сложение их модулей;
• дописать к полученной сумме знак «–».

Согласно правилу сложения можно записать:

$(−a)+(−b)=−(a+b)$.

Правило сложения отрицательных чисел применяется к отрицательным целым, рациональным и действительным числам.

Пример 1

Сложить отрицательные числа $−185$ и $−23 \ 789.$

Решение.

Воспользуемся правилом сложения отрицательных чисел.

Найдем модули данных чисел:

$|-185|=185$;

$|-23 \ 789|=23 \ 789$.

Выполним сложение полученных чисел:

$185+23 \ 789=23 \ 974$.

Поставим знак $«–»$ перед найденным числом и получим $−23 \ 974$.

Краткая запись решения: $(−185)+(−23 \ 789)=−(185+23 \ 789)=−23 \ 974$.

Ответ: $−23 \ 974$.

При сложении отрицательных рациональных чисел их необходимо преобразовать к виду натуральных чисел, обыкновенных или десятичных дробей.

Пример 2

Сложить отрицательные числа $-\frac{1}{4}$ и $−7,15$.

Решение.

Согласно правилу сложения отрицательных чисел, сначала необходимо найти сумму модулей:

$|-\frac{1}{4}|=\frac{1}{4}$;

$|-7,15|=7,15$.

Полученные значения удобно свести к десятичным дробям и выполнить их сложение:

$\frac{1}{4}=0,25$;

$0,25+7,15=7,40$.

Поставим перед полученным значением знак $«–»$ и получим $–7,4$.

Краткая запись решения:

$(-\frac{1}{4})+(−7,15)=−( \frac{1}{4}+7,15)=–(0,25+7,15)=−7,4$.

Ответ: $–7,4$.

Как вычитать числа с разными знаками

Правило сложения чисел с противоположными знаками:

Для сложения положительного и отрицательного числа необходимо:

1. вычислить модули чисел;

2. выполнить сравнение полученных чисел:

   • если они равны, то исходные числа являются противоположными и их сумма равна нулю;
   • если они не равны, то нужно запомнить знак числа, у которого модуль больше;

3. из большего модуля вычесть меньший;

4. перед полученным значением поставить знак того числа, у которого модуль больше.

Сложение чисел с противоположными знаками сводится к вычитанию из большего положительного числа меньшего отрицательного числа.

Правило сложения чисел с противоположными знаками выполняется для целых, рациональных и действительных чисел.

Пример 3

Сложить числа $4$ и $−8$.

Решение.

Требуется выполнить сложение чисел с противоположными знаками. Воспользуемся соответствующим правилом сложения.

Найдем модули данных чисел:

$|4|=4$;

$|-8|=8$.

Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.

Далее от большего модуля отнимем меньший модуль, получим:

$8−4=4$.

Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$

Краткая запись решения:

$4+(–8) = –(8–4) = –4$.

Ответ: $4+(−8)=−4$.

Для сложения рациональных чисел с противоположными знаками их удобно представить в виде обыкновенных или десятичных дробей.

Вычитание чисел с разными и отрицательными знаками

Правило вычитания отрицательных чисел:

Для вычитания из числа $a$ отрицательного числа $b$ необходимо к уменьшаемому $a$ добавить число $−b$, которое является противоположным вычитаемому $b$.

Согласно правилу вычитания можно записать:

$a−b=a+(−b)$.

Данное правило справедливо для целых, рациональных и действительных чисел. Правило можно использовать при вычитании отрицательного числа из положительного числа, из отрицательного числа и из нуля.

Пример 4

Вычесть из отрицательного числа $−28$ отрицательное число $−5$.

Решение.

Противоположное число для числа $–5$ – это число $5$.

Согласно правилу вычитания отрицательных чисел получим:

$(−28)−(−5)=(−28)+5$.

Выполним сложение чисел с противоположными знаками:

$(−28)+5=−(28−5)=−23$.

Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

Ответ: $(−28)−(−5)=−23$.

При вычитании отрицательных дробных чисел необходимо выполнить преобразование чисел к виду обыкновенных дробей, смешанных чисел или десятичных дробей.

Сложение и вычитание чисел с разными знаками

Правило вычитания чисел с противоположными знаками совпадает с правилом вычитания отрицательных чисел.

Пример 5

Вычесть положительное число $7$ из отрицательного числа $−11$.

Решение.

Противоположное число для числа $7$ – это число $–7$.

Согласно правилу вычитания чисел с противоположными знаками получим:

$(−11)−7=(–11)+(−7)$.

Выполним сложение отрицательных чисел:

$(−11)+(–7)=−(11+7)=−18$.

Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

Ответ: $(−11)−7=−18$.

При вычитании дробных чисел с разными знаками необходимо выполнить преобразование чисел к виду обыкновенных или десятичных дробей.

spravochnick.ru

правило, примеры, выполните сложение отрицательных чисел по правилу

В рамках этого материала мы затронем такую важную тему, как сложение отрицательных чисел. В первом параграфе мы расскажем основное правило для этого действия, а во втором – разберем конкретные примеры решения подобных задач.

Yandex.RTB R-A-339285-1

Основное правило сложения натуральных чисел

Перед тем, как вывести правило, вспомним, что мы вообще знаем о положительных и отрицательных числах. Ранее мы условились, что отрицательные числа нужно воспринимать как долг, убыток. Модуль отрицательного числа выражает точные размеры этого убытка. Тогда сложение отрицательных чисел можно представить как сложение двух убытков.

Воспользовавшись этим рассуждением, сформулируем основное правило сложения отрицательных чисел.

Определение 1

Для того чтобы выполнить сложение отрицательных чисел, нужно сложить значения их модулей и поставить минус перед полученным результатом. В буквенном виде формула выглядит как (−a)+(−b)=−(a+b).

Исходя из этого правила, можно сделать вывод, что сложение отрицательных чисел аналогично сложению положительных, только в итоге у нас обязательно должно получиться отрицательное число, ведь перед суммой модулей надо ставить знак минус.

Какие можно привести доказательства этого правила? Для этого нам потребуется вспомнить основные свойства действий с действительными числами (или с целыми, или с рациональными  –они одинаковы для всех этих типов чисел). Для доказательства нам нужно всего лишь продемонстрировать, что разность левой и правой части равенства (−a)+(−b)=−(a+b) будет равна 0.

Вычесть одно число из другого – это то же самое, что и прибавить к нему такое же противоположное число. Следовательно, (−a)+(−b)−(−(a+b))=(−a)+(−b)+(a+b). Вспомним, что числовые выражения со сложением обладают двумя основными свойствами – сочетательным и переместительным. Тогда мы можем сделать вывод, что (−a)+(−b)+(a+b)=(−a+a)+(−b+b). Поскольку, сложив противоположные числа, мы всегда получаем 0, то (−a+a)+(−b+b)=0+0, а 0+0=0.Наше равенство можно считать доказанным, значит, и правило сложения отрицательных чисел мы тоже доказали.

Задачи на сложение отрицательных чисел

Во втором параграфе мы возьмем конкретные задачи, где нужно складывать отрицательные числа,

zaochnik.com

Отрицательные числа

Владение отрицательными числами — необязательный навык, если Вы собираетесь поступать в 5 класс физико-математической школы. Однако это намного упростит решение уравнений, что дальше отразится на общем результате

вступительной олимпиады.

Итак, приступим.
Сперва надо понять, что существуют числа меньше нуля, которые и называются отрицательными: например на единицу меньше, чем это , ещё на единицу меньше 1, далее , а потом и т. д. У любого натурального числа есть свой «отрицательный брат», число , которое в сумме с исходным числом даёт .

Все натуральные, «минус натуральные» числа и «0» вместе составляют множество целых чисел.

Сложение и вычитание

Если представить себе числовую прямую, то можно легко овладеть правилами сложения и вычитания отрицательных чисел: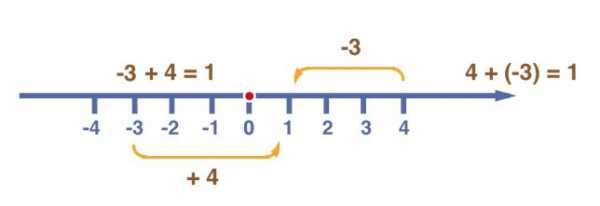

Сперва находите на прямой то число, к которому или из которого вы будете вычитать/прибавлять. Дальше, если Вам нужно:

1. Прибавить отрицательное число, то необходимо сместиться влево
2. Прибавить положительное число — сместиться вправо
3. Вычесть отрицательное — сместиться вправо
4. Вычесть положительное — сместиться влево

на то число единиц, которое вы прибавляете/вычитаете. Новое место, где Вы окажетесь, и будет результатом операции.

Разумеется, задачи для для поступления в 5 класс можно будет решить и без использования отрицательных чисел, но это улучшит Ваш математический уровень в общем. Со временем Вы не будете рисовать или представлять числовую прямую, а будете делать это «на автомате», но для этого стоит потренироваться: придумайте любые числа (отрицательных или положительных) и попробуйте их сперва сложить, потом вычесть. Повторяя такое упражнение по раз в день уже через дня Вы почувствуете, что полностью научились складывать и вычитать любые целые числа.

Умножение и деление

Здесь ситуация ещё проще: необходимо лишь запомнить как меняются знаки при умножении или делении:

1. на
2. на
3. на
4. на

Вместо слова «на» может стоять как умножение, так и деление.
Со знаком мы определимся, а само число — это результат соответственно умножения или деления исходных чисел без знаков.

Примеры сложения, вычитания, умножения и деления отрицательных чисел

1. 
   Смещается вправо на
2. 
   Смещается влево на
3. 
   Смещаемся вправо на : разобьём на два шага — до «» и «сколько осталось»
4. 
   Смещаемся влево на
5. 
   Зак будет , затем просто перемножаем
6. 
   Зак будет , затем просто перемножаем
7. 
   Зак будет , затем просто делим
8. 
   Зак будет , затем просто делим

geniusmath.ru

6 класс. Математика. Вычитание положительных и отрицательных чисел — Вычитание

Комментарии преподавателя

Этим уро­ком мы за­кан­чи­ва­ем изу­че­ние раз­де­ла «Сло­же­ние и вы­чи­та­ние по­ло­жи­тель­ных и от­ри­ца­тель­ных чисел». По­лу­чен­ные при изу­че­нии этого раз­де­ла зна­ния поз­во­лят нам по­смот­реть на хо­ро­шо зна­ко­мое ариф­ме­ти­че­ское дей­ствие вы­чи­та­ние дру­гим гла­за­ми.

Вы­чи­та­ние – это дей­ствие, об­рат­ное сло­же­нию.

Если нас про­сят, на­при­мер, вы­честь 8 из 11, то нам надо найти число, ко­то­рое нужно при­ба­вить к 8, чтобы по­лу­чить 11. Ясно, что это число 3. С дру­гой сто­ро­ны, если к 11 при­ба­вить  , мы тоже по­лу­чим 3.

Таким об­ра­зом, вы­честь 8 и при­ба­вить    – это одно и то же дей­ствие.

Сфор­му­ли­ру­ем пра­ви­ло.

Чтобы из дан­но­го числа вы­честь дру­гое, надо к умень­ша­е­мо­му при­ба­вить число, про­ти­во­по­лож­ное вы­чи­та­е­мо­му.

При­мер1.

Для того чтобы из  вы­честь  , за­ме­ним вы­чи­та­ние сло­же­ни­ем, а число 14 – ему про­ти­во­по­лож­ным. Вы­пол­ним сло­же­ние от­ри­ца­тель­ных чисел.

При­мер 2.

Для того чтобы из  вы­честь , за­ме­ним вы­чи­та­ние сло­же­ни­ем. Затем сло­жим числа с раз­ны­ми зна­ка­ми.

При­мер 3.

Вы­чтем из числа 10 число . За­ме­ним вы­чи­та­ние сло­же­ни­ем, а число  – ему про­ти­во­по­лож­ным. По­лу­чим число 13. За­ме­тим, что в дан­ном при­ме­ре два знака минус, ко­то­рые сле­до­ва­ли друг за дру­гом, мы за­ме­ни­ли зна­ком плюс. Это удоб­ный тех­ни­че­ский прием.

За­ме­тим, что в по­доб­ных слу­ча­ях его при­ме­ня­ют все­гда. При этом про­ме­жу­точ­ные рас­суж­де­ния опус­ка­ют.

При­мер 1.

В этом при­ме­ре два знака минус идут под­ряд. Их можно за­ме­нить зна­ком плюс.

 

При­мер 2.

За­ме­ним два знака минус, иду­щих под­ряд, зна­ком плюс.

При­мер 3.

Вос­поль­зу­ем­ся пра­ви­лом, за­ме­ним два знака минус, ко­то­рые сле­ду­ют друг за дру­гом, зна­ком плюс.

Сфор­му­ли­ру­ем за­ме­ча­ние.

Любое вы­ра­же­ние, со­дер­жа­щее лишь знаки сло­же­ния и вы­чи­та­ния, можно рас­смат­ри­вать как сумму.

Упраж­не­ние. Рас­смот­ри­те дан­ные вы­ра­же­ния и ука­жи­те каж­дое сла­га­е­мое в сумме.

        Это сумма числа .

www.kursoteka.ru

Памятка «Алгоритм сложения и вычитания положительных и отрицательных чисел»

1.Уменьшаемое записываем без изменения;

2.Знак вычитания заменяем знаком сложения;

3.Вычитаемое заменяем противоположным числом;

4. Применяем правило сложения.

Примеры:

-8 – (- 2)= -8 + 2 = -6;

6 – 9 = 6 +( — 9) = — 3.

1.Выделяем число, модуль которого больше;

2.В ответе ставим знак того числа, модуль которого больше;

3.Модули вычитаем.

Примеры:

-7 + 5= — 2;

9+ (- 4) = +5 = 5.

1.В ответе ставим знак минус;

2.Модули складываем.

Пример:

-9 + ( — 5) = — 14

В ответе всегда получается 0.

Примеры:

-7 + 7 = 0;

3 + (- 3)= 0.

чисел с разными знаками

отрицательных

чисел

вычитание

противоположных

чисел

сложение

действие

Алгоритм сложения и вычитания положительных и отрицательных чисел.

infourok.ru

Сложение положительных и отрицательных чисел

Технологическая карта

Класс 6 «В»

Тема урока: «Сложение положительных и отрицательных чисел»

Место урока в теме: 1

Тип урока: изучение нового материал с первичным закреплением

Цель урока:

• образовательная: сформирование представление о сложении рациональных чисел; организовать деятельность учащихся для нахождения правила (алгоритма) сложения чисел с одинаковыми и разными знаками; применить полученные знания при решении заданий и задач; проверить уровень усвоения знаний;

• -воспитательная: воспитывать интерес к математике, применяя интересные задания, используя различные формы работы.

• -развивающая: развивать умение учащихся работать как индивидуально (самостоятельно), так и коллективно; развивать умение оценить свои силы, используя задания разного уровня сложности.

Прогнозируемый результат:

• Умение складывать положительные числа.

• Умение складывать отрицательные числа.

• Умение складывать положительные и отрицательные числа.

• Умение формулировать правила, алгоритмы сложения положительных и отрицательных чисел.

Формы организации учебной деятельности учащихся:

Ход урока

1 этап. Организационно-психологический (время- мин)

Деятельность учителя	Деятельность учащегося	Электронно-образовательные ресурсы (ЭОР) и оборудование
Проверить уровень готовности учащихся к уроку. Настроить на положительное настроение на уроке.	Готовность к уроку	Презентация «Сложение положительных и отрицательных чисел», слайд 1

2 этап. Проверка домашнего задания (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
	Проверяют домашнее задание	Презентация «Сложение положительных и отрицательных чисел», слайд 2

3 этап. Актуализация опорных знаний (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
Задание 1 На слайде написаны числа: . Запишите наибольшее число. Запишите наименьшее число. Запишите модуль наибольшего числа. Запишите модуль наименьшего числа. Какие числа в ряду являются противоположными? Запишите числа в порядке возрастания. Найдите сумму всех записанных рациональных чисел.	Записывают ответы в тетради (индивидуально), а затем проверить с помощью презентации. (7 задание мы пока выполнить не можем)	Презентация «Сложение положительных и отрицательных чисел», слайд 3

4 этап. Мотивационно-целевой (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
— А так как мы не можем выполнить задание 7 с имеющимися знаниями. Какая тема урока? -Давайте уточним тему урока. И поставим цель урока. Какие числа называются рациональными? — тема «Сложение положительных и отрицательных чисел» — Какие цели поставим на урок?	— Сложение рациональных чисел. -положительные и отрицательные числа и нулю. -узнать правило сложения положительных и отрицательных чисел -применять данные правила при решении заданий и задач	Презентация «Сложение положительных и отрицательных чисел», слайд 4, 5

5 этап. Изучение нового материала(время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
Делим ребят на 5 групп, каждой группе раздать карточки и термометры. Проверить правила сложения положительных и отрицательных чисел.	Заполняют карточку с помощью термометра (приложение 1). Находят правила сложения положительных и отрицательных чисел. Каждая группа озвучивает получившиеся правила.	Термометры и карточки. Презентация «Сложение положительных и отрицательных чисел», слайд 6-7

6 этап. Практическое применение знаний (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
Доделываем в задании 1(7). Проверяет задания 670 (а-л) (устно), 673 (а-в, к-м), 672 (а-б)	Доделывают в задании 1(7). Выполняют задания в тетрадях, один ученик у доски.	Презентация «Сложение положительных и отрицательных чисел», слайд 8-9

7 этап. Определение уровня и качества знаний учащихся (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
-сейчас мы проверим, все ли поняли данные правила.	Работа по вариантам. В конце проверка между вариантами с помощью презентации.	Презентация «Сложение положительных и отрицательных чисел», слайд 10

8 этап. Рефлексивно-оценочный (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
На доске нарисован термометр, у вас на столах лежат стикеры: если понравился урок и все было понятно вы клеите его выше 0 если остались вопросы по теме клеите в 0 если ничего не было понятно, то ниже 0	Клеят стикеры	Плакат

9 этап. Информация о домашнем задании (время- мин)

Деятельность учителя	Деятельность учащегося	ЭОР и оборудование
Выучить правила и выполнить задания в тетрадях	Записывают домашнее задание :параграф15(А)№670(н-т) (устно), 673 (г-е), 672 (г)	Презентация «Сложение положительных и отрицательных чисел», слайд 11

Карточка 1

Занесите данные в таблицу с помощью термометра:

Было температура	+5	+5	+5	+5	+5	+5	+5	– 3	– 3	– 3
Изменилась на	+3	+2	– 4	– 2	– 5	– 8	– 9	+2	– 1	– 2
Стало температура

Заполните пропуски в примерах с помощью таблицы:

1) (+5)+(+3)=___; 2) (+5)+(+2)=___; 3) (+5)+( –4)=___; 4) (+5)+( –2)=___;

5) (+5)+( –5)=___; 6) (+5)+( –8)=___; 7) (+5)+( –9)=___; 8) (–3)+( +2)=___;

9) (–3)+( – 1)=___; 10) (–3)+( – 2)=___.

Правило сложения рациональных чисел с одинаковыми знаками: __________________________

__________________________________________________________________________________

__________________________________________________________________________________

Укажите номера примеров, которые соответствуют этому правилу:_________________________

Правило сложения рациональных чисел с разными знаками: ______________________________

__________________________________________________________________________________

__________________________________________________________________________________

Укажите номера примеров, которые соответствуют этому правилу:_________________________

__________________________________________________________________________________

Вариант 1 Выполните действия: 37 + (–56) –46 + 86 –58+(–92) 4,61+ (–2,36) –8,34+1,34 32+(–48)+20 –36 + (– 12) + 74

Вариант 2 Выполните действия: 41 + (–69) –65 + 87 – 18 + (–77) 4,71+ (–2,96) –6,34+3,34 28 + (–39) + 18 –18 + (– 15) + 64

Вариант 1 Выполните действия: 37 + (–56) –46 + 86 –58+(–92) 4,61+ (–2,36) –8,34+1,34 32+(–48)+20 –36 + (– 12) + 74	Вариант 2 Выполните действия: 41 + (–69) –65 + 87 – 18 + (–77) 4,71+ (–2,96) –6,34+3,34 28 + (–39) + 18 –18 + (– 15) + 64
Вариант 1 Выполните действия: 37 + (–56) –46 + 86 –58+(–92) 4,61+ (–2,36) –8,34+1,34 32+(–48)+20 –36 + (– 12) + 74	Вариант 2 Выполните действия: 41 + (–69) –65 + 87 – 18 + (–77) 4,71+ (–2,96) –6,34+3,34 28 + (–39) + 18 –18 + (– 15) + 64
Вариант 1 Выполните действия: 37 + (–56) –46 + 86 –58+(–92) 4,61+ (–2,36) –8,34+1,34 32+(–48)+20 –36 + (– 12) + 74	Вариант 2 Выполните действия: 41 + (–69) –65 + 87 – 18 + (–77) 4,71+ (–2,96) –6,34+3,34 28 + (–39) + 18 –18 + (– 15) + 64

videouroki.net

сложение и вычитание положительных и отрицательных чисел

Слайд 1

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ Островская Таисия Алексеевна Учитель математики МБОУ лицея № 15 у ченица Репина Ксения

Слайд 2

О бщее правило при сложении и вычитании рациональных чисел.

Слайд 3

ЗНАЕШЬ ЛИ ТЫ? 1. Что такое положительное и что такое отрицательное число? 2. Как они располагаются на числовом луче? 3. Как сравнить положительные и отрицательные числа?

Слайд 4

ПРОВЕРЬ СЕБЯ ! Выпиши все положительные и все отрицательные числа : — 7; 9 ,2; — 10,5; 73 ; — 55 ,99; — 0,056; 123; 41,9; — 0,4 Расположи их в порядке возрастания. Расположи их в порядке убывания .

Слайд 5

ОТВЕТЫ: 9,2; 73; 123; 41,9; ( + ) -7; -10,5; — 55 ,99; — 0,056; — 0,4. ( — ) В порядке возрастания: — 55 ,99 ; -10,5 ;-7;-0,4; — 0,056; 9, 2 ; 41,9;73; 123; В порядке убывания: 123;73; 41,9;9,2; — 0,056; — 0,4;-7; — 10,5; -55,99 .

Слайд 6

Правила. 1. Числа, меньше нуля, называют отрицательными. И ставят знак (-). Числа, больше нуля, называют положительными. И ставят знак (+). Число 0 (нуль) не относится ни к положительным, ни к отрицательным числам. │0│= 0; 2. Расстояние от точки, изображающей число, до 0 называется МОДУЛЕМ числа и всегда положительно, как любое расстояние. Модуль обозначают двумя черточками: │5│= 5; │-5│= 5; Модули противоположных чисел РАВНЫ: │-6│=│6 │Модуль положительного числа равен самому числу. │5│ = │5│

Слайд 7

Правила . 3. Чем число больше, тем правее оно лежит на числовой оси. 4. Из двух отрицательных чисел больше то, у которого модуль меньше. 5. Числа, имеющие одинаковые модули, но отличающиеся знаком, называются противоположными.

Слайд 8

СЛОЖЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ 1. Чтобы сложить отрицательные числа, нужно: а). Поставить известный сразу знак результата – «минус»; б). Сложить модули чисел: ( — 3,5 ) + ( — 4,8 ) = — (3,5 + 4,8) = — 8,3 Реши самостоятельно: (- 6,7 ) + ( — 23,3 ) = ? ( — 75,6 ) + (- 5,7) = ? ( — 46,2 ) + ( — 55 ) = ? 2. А что происходит если складывать числа с разными знаками? 6 + (- 2 ) = … ; 1 + ( — 3 ) = … ?

Слайд 9

Задачка Во вpемя сильного дождя на остановке автобуса стояли 12 человек. Подкатил автобус и забpызгал гpязью пятеpых . Остальные успели попpыгать в колючие кусты. Сколько исцаpапанных пассажиpов поедет в автобусе, если известно, что тpое так и не смогли выбpаться из колючих кустов ?

Слайд 10

При сложении чисел с разными знаками знак результата совпадает со знаком того числа, модуль которого больше, а сам ответ определяется действием вычитания . Объясни, как были решены примеры: ( — 17 ) + 7 = — (17 – 7) = — 10 12 + ( — 20 ) = — (20 -12) = — 8 А теперь сам, пользуясь правилом, подробно запиши решения следующих примеров: 1). (-3) + 5 =… ; 2). 7 + (- 4 ) = … ; 3). (-10) + 3 = … ; 4). (-22) + 33 = … ; 5). ( 5 ) + ( -9 ) = … ; 6). (1,7) + ( — 3,9 ) = … ; 7). 17 + ( — 40 ) = …?

Слайд 11

ПРОВЕРЬ СВОИ РЕШЕНИЯ ! 1). 2 2). 3 3). — 7 4). 11 5). -4 6). — 2,2 7). — 23

Слайд 12

ЗАДАЧКА Во вpемя игpы в пpятки 5 мальчиков спpятались в бочку из под известки, 7 — в бочку из-под зеленой кpаски , 4 — в бочку из-под кpасной и девять — в ящик из-под угля. Мальчик, котоpый пошел их искать, нечаянно упал в бочку из-под желтой кpаски . Сколько pазноцветных мальчиков и сколько чеpно-белых мальчиков игpало в пpятки ?

Слайд 13

АЛГОРИТМ СЛОЖЕНИЯ. НУЖНО СООБРАЗИТЬ: ЧИСЛА «дружат» ? (ЗНАКИ ОДИНАКОВЫЕ) Числа «ссорятся» ? (ЗНАКИ РАЗНЫЕ) Поставить у результата тот же знак и сложить модули чисел. 4 + 5=9 — 4 +(-5) = — 9 Реши примеры: 5 + 8 = …; (- 5) + ( — 11 ) = … ( — 8,1 ) + (- 0,7) = … (-2) + (-8) = … (-49) + (-13) = … Поставить у результата знак «победителя» и из большего модуля вычесть меньший. 3 +(-8 ) = — (8 -3)= -5 6 + (-4) = + ( 6-4) = 2 Реши примеры: (-2) + (8) = …; 3,5 +(-10) =… 18 + (-5,7) = … (-11) + 5 = …

Слайд 14

ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ. Вычитание можно заменить сложением с Числом, противоположным вычитаемому: 9 – (-3) = 9 + (+3) = 9 +3=12 Мы заменили вычитание сложением с числом противоположным. Кратко можно записать так : 9 – ( — 3 ) = 9 + 3 = 12; Два минуса перед числом превратились в плюс: -( — 3 ) = + 3 Потренируемся : 2 – ( — 7 ) =… — 10 – ( — 15 = — 10 + 15 = 15 – 10 = 5;- — 25 – ( -4 ) = — 25 + 4 = — 21

Слайд 15

Если перед числом стоят два одинаковых знака ( — — ) или ( + + ), то они меняются на ( + ). 3 – (-7) = 3 +7 = 10 12 – ( + 8 ) = 12 – 8 = … (-9) – (-5) =…. 6 + ( — 10 ) = 6 – 10 = … 15 + (+10)=…. Видно, что если перед числом стоят 2 разных знака ( + — ) или ( — + ), то они заменяются на минус ( — ) !

Слайд 16

Проверь свое решение 1. …. = 10 4. …. = — 4 2. …. = 4 5. …. = + 25 3. …. = — 4 ПРАВИЛЬНО! МОЛОДЦЫ!

Слайд 17

ЗАДАЧКА Один дедушка охотился в кухне на таpаканов и убил пятеpых , а pанил в тpи pаза больше. Тpех таpаканов дедушка pанил смеpтельно , и они погибли от pан , а остальные pаненые таpаканы выздоpовели , но обиделись на дедушку и навсегда ушли к соседям. Сколько таpаканов ушли к соседям навсегда?

Слайд 18

РЕШИ ПРИМЕРЫ САМ: 21 + ( — 8 ) =…; -10 + ( — 16 ) =…; — 7 – ( -15 ) = …; 3 – ( — 11 ) =… ; — 32 – ( — 22 ) = …; 16 – ( + 5 ) = … ; 5 – ( + 15) = … ; 2 – ( — 9 ) = … ; — 13 + ( — 18 ) = … ; — 49 + ( — 10 ) = … ; — 15 – ( — 21 ) = … ; 6 – ( + 10 ) = … ;

Слайд 19

Проверь свои ответы 1. = 13 2. = -26 3. = 8 4. = 14 5. = -10 6. = 11 Правильное решение! 7. = 10 8. = 11 9. = 31 10. = -59 11. = 6 12. = -4 МОЛОДЦЫ!

Слайд 20

Усложним задачу и попробуем решить длинные примеры, используя те же правила : 5 – ( — 8 )+ (-12) – (+ 5 ) +17 – 10 – ( — 2 ) = = 5 +8 -12 – 5 + 17- 10 + 2= (8+17+2) + (-12-10)= = 27 + ( — 22 ) 27 -22 = 5 Запомни алгоритм вычисления: Отбросим скобки, используя правило превращения знаков « кошки-собаки»; Получилась алгебраическая сумма. Можно взаимно уничтожить противоположные по знакам слагаемые +5 и — 5; Сгруппируем отдельно (+) и (-) слагаемые; Найдем результат.

Слайд 21

ЗАДАЧКА Допустим , что ты pешил пpыгнуть в воду с высоты 8метpов и, пpолетев 5 метpов , пеpедумал . Сколько метpов пpидется тебе еще лететь поневоле?

nsportal.ru