Свойства предела функции
Следующие свойства предела функции вытекают из аналогичных свойств предела последовательности с применением теоремы 2.
LIM1. Константная функция имеет предел, равный этой же константе
Пусть существую пределы . Тогда
LIM2. Предел суммы существует и равен сумме пределов:.
LIM3. Предел произведения существует и равен произведению пределов:. В частности, константу можно выносить за знак предела.
LIM4. Предел отношения существует и равен отношению пределов в том случае, когда предел знаменателя отличен от 0.
Следующие свойства LIM5-LIM7 описывают предельный переход в неравенствах.
LIM5. Еслипри любом x из некоторой малой окрестности точки a, то и(при условии существования предела). Аналогично свойство имеет место для неравенства «≤ «.
Как следствие предыдущего свойства получаем монотонность предела:
LIM6. Предположим, чтодля любогоблизкого к a. Тогда ипри условии существования этих пределов.
Следующее свойство называется теоремой о пределе промежуточной функции
LIM7.(предел промежуточной функции)Предположим, чтодля любогоиз некоторой проколотой окрестности точки. Предположим также, что пределыисуществуют и совпадают между собой. Тогда и предел промежуточной функцииприсуществует и совпадает с пределами крайних функций.
LIM8. (предел сложной функции) Предположим, что
Тогда существует предел сложной функции прии он равен A.
Доказательство. Фиксируем . Находимтакое, чтодля любого. Для этогонаходимтакое, что как только, то. Тогда и неравенствотакже будет выполнено для любого, удовлетворяющего неравенствам.□
Бесконечно малые величины
Функция , определенная в некоторой проколотой окрестности точкиназывается бесконечно малой при, если.
Свойства бесконечно малых величин вытекают из соответствующих свойств предела:
M1. Сумма бесконечно малых величин суть бесконечно малая величина.
Функция называется ограниченной в точке, если найдется такая окрестность этой точки и такая константа, чтодля всехиз этой окрестности.
Предложение.Функция, имеющая предел в точке, ограничена в этой точке. Более того, если, тоограничена в точке a.
Доказательство. Если для любых, то для любыхиз -окрестности точкиимеет место оценка
Докажем второе утверждение. Полагаем . Для𝜺=A/2 найдем δ такое, что. Тогдаидля всех x из δ-окрестности точки. Аналогично разбирается случай A<0.□
M2. Произведение бесконечно малой величины на функцию, ограниченную в точке, является бесконечной малой величиной. В частности, произведение б.м. на функцию, имеющую предел в точкесуть также б.м., а также произведение нескольких б.м. есть б.м.
М3. Произведение б.м. на константу есть б. м.
M4.Отношение б.м. к функции, имеющий ненулевой предел в точкеявляется б.м.
Действительно, если , тоограничена в точке a по выше доказанному в предложении. Следовательно, на основании свойства М2 получаем, чтотакже есть б.м.
М5. Пусть(x) — бесконечно малая при, а— функция такая, что выполняется неравенстводля всех x из достаточно малой проколотой окрестности точки. Тогдатакже будет б.м.
Это свойство верно в силу теоремы о пределе промежуточной функции.
studfiles.net
Тема 4 Предел и непрерывность.
Предел числовой последовательности. Предел монотонной последовательности. Свойства предела. Предельный переход в неравенствах. Число e.
Предел функции. Свойства предела функции.
Замечательные пределы.
Непрерывность. Свойства непрерывных функций. Устойчивость знака.
Функции непрерывные на отрезке. Принцип непрерывности.
Предел последовательности вещественных чисел
Неравенство задает интервал, который называется𝜺-окрестностью точки (числа)Заметим, что любой интервал, содержащий точку, включает в себя-окрестность при достаточно малом
Определение.Числоназывается пределом последовательности(записывается), если для любого положительного𝜺найдется натуральное N такое, чтодля всех.
Пример.Докажем, что lim 1/n =0. Возьмём𝜺>0. Неравенство |1/n-0| <𝜺выполнено, если n>1/𝜺. В качестве N(𝜺) можно взять [1/𝜺]+1 — наименьшее натуральное число, превосходящее 1/𝜺. Здесь черезобозначена целая часть числа, т.е. наибольшее целое число, не превосходящее.
Теорема.Любая монотонно возрастающая ограниченная сверху последовательностьимеет предел и он равен. Аналогично, любая монотонно убывающая и ограниченная снизу последовательность имеет предел равный точной нижней грани множества значений этой последовательности.
Доказательство. Пусть — монотонно возрастающая и ограниченная сверху последовательность. Обозначим. Пусть𝜺>0. Так как число u-𝜺не является верхней гранью значений нашей последовательности, то найдется натуральное N такое, что. Тогда для любого n≥ N имеем
в силу монотонности последовательности и того факта, что u — верхняя грань. Отсюда для любого натурального n≥ N следует неравенство<𝜺, что и требовалось доказать.□
Свойства предела
А.Если предел существует, то он единственен
Б.Предел суммы равен сумме пределов, если пределы слагаемых существуют.
Пусть ,. Фиксируем𝜺>0. Находимтакое, что для любоговыполняется неравенство. Аналогично, находимтакое, что для любоговыполняется неравенство. Тогда для любоговыполняется оценка
В.Предел константной последовательности равен этой константе
Последовательность называется ограниченной, если найдется константатакая, чтодля всех. Для доказательства следующего свойства нужна
Г. Любая сходящаяся последовательностьограничена.
Д.Предел произведения равен произведению пределов, при условии, что пределы сомножителей существуют.
Е.Константу можно выносить за знак предела:
Это утверждение есть следствие свойств Д и В.
Ж.Предел отношения равен отношению пределов, если пределы числителя и знаменателя существуют и последний не равен нулю.
На основе предела можно вычислять другие пределы, пользуясь уже не определением, а правилами А-Е. Например,
Опишем теперь предельные переходы в неравенствах.
З.Если выполняется неравенствоначиная с некоторого N, и предел последовательностисуществует, то. Аналогичное свойство имеет место для неравенства ≤ .
Действительно, если , то длянайдется N, начиная с которого. Тогда.
Заметим, что для строгих неравенств аналогичное утверждение несправедливо. Например, 1/n>0 для любого n, но lim 1/n=0, как мы доказали выше.
И. Если выполняется неравенствоначиная с некоторого N, топри условии, что эти пределы существуют.
Действительно, так как для всех, тосогласно свойства Ж. Тогда, применяя свойства Б и Д, получим
К (предел промежуточной последовательности). Еслиначиная с некоторого номера, а пределы крайних последовательностей существуют и равны одному и тому же числу A, то пределтакже существует и равен A.
studfiles.net
4.3. Свойства функций, имеющих предел
Теорема 4.2. Если функция в данной точке 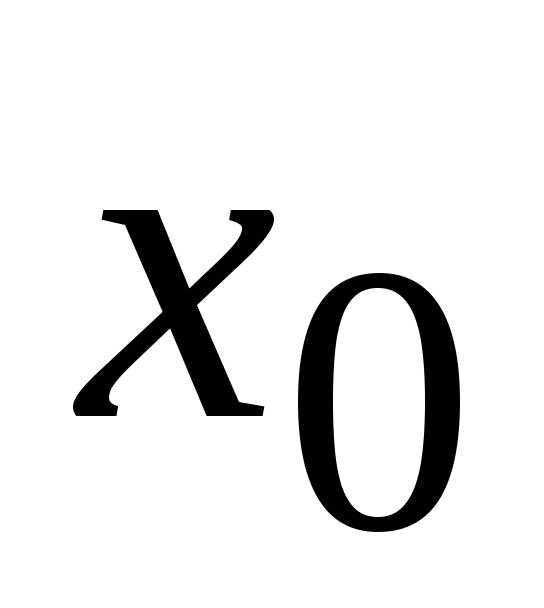 имеет предел, то она ограничена в
некоторой окрестности точки
имеет предел, то она ограничена в
некоторой окрестности точки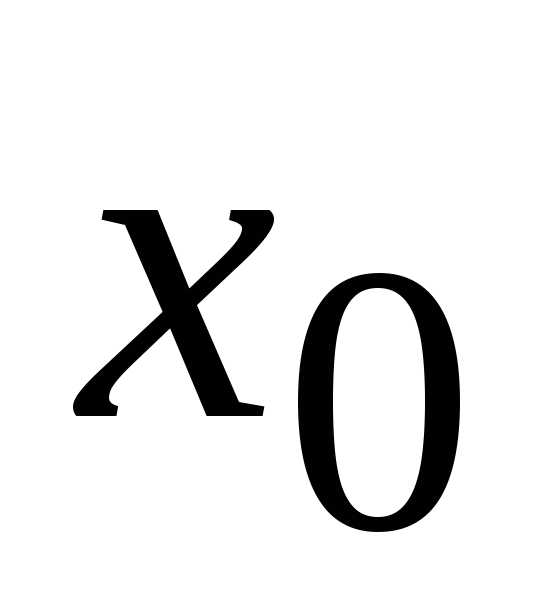
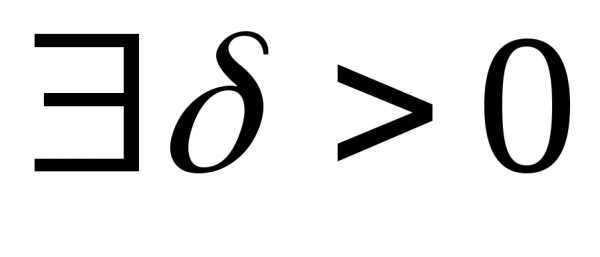 ,
, 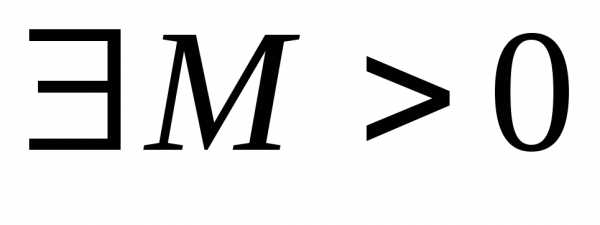 ,
,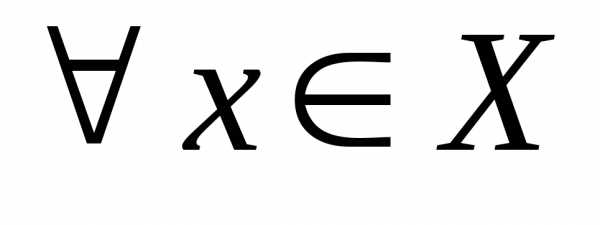 :
: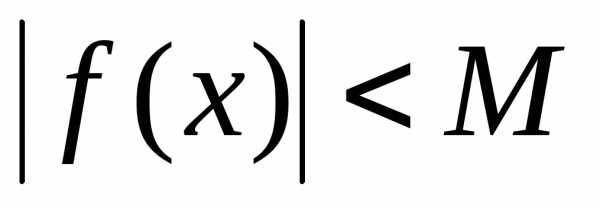 .
.
Доказательство. Обозначим
и рассмотрим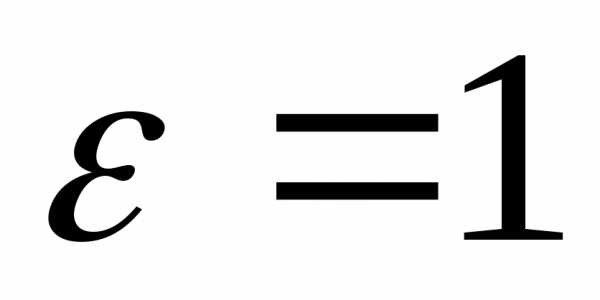 . Из определения
4.3. следует существование такого
. Из определения
4.3. следует существование такого 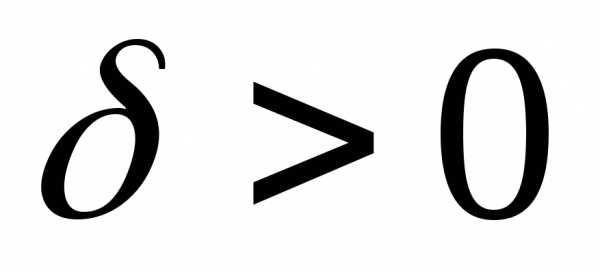 ,
что для всякого
,
что для всякого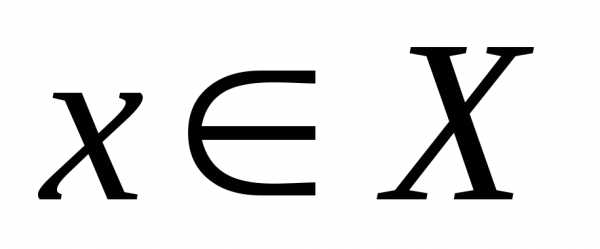 из
неравенстввытекает неравенство.
Остается положить.Теорема
доказана.
из
неравенстввытекает неравенство.
Остается положить.Теорема
доказана.
Использование определения предела функции по Гейне позволяет перенести утверждения, доказанные ранее для последовательностей, на случай произвольных функций.
Теорема
4.3. Пусть функции 
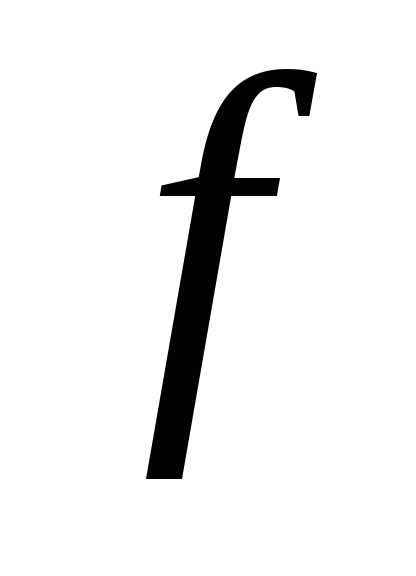 и
и определены на множестве
определены на множестве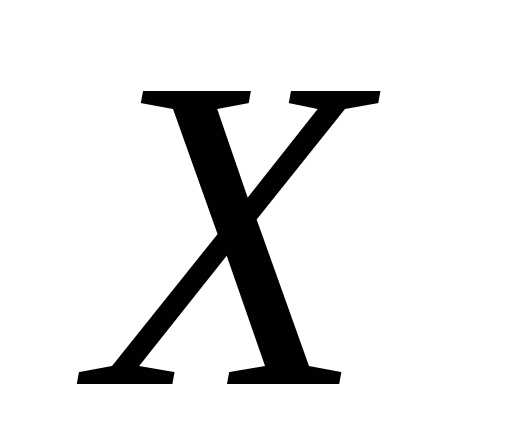 ,
на котором выполняются неравенства.
Пусть существуют
,
на котором выполняются неравенства.
Пусть существуют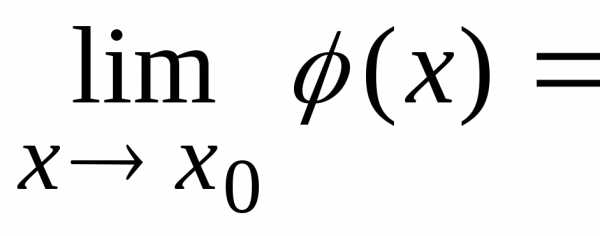 ,
тогда.
,
тогда.Доказательство непосредственно вытекает из определения предела функции по Гейне и леммы о двух милиционерах.
Теорема
4.4. Пусть функции 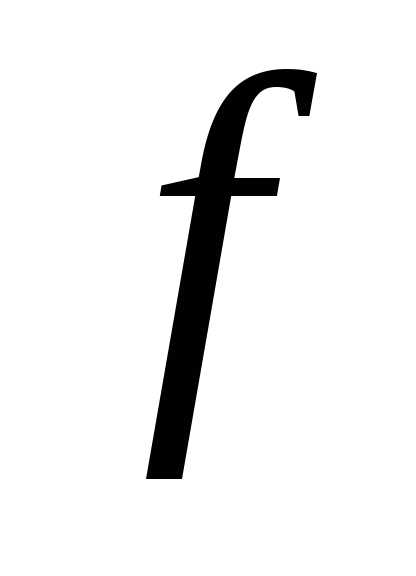 и
и определены на множестве
определены на множестве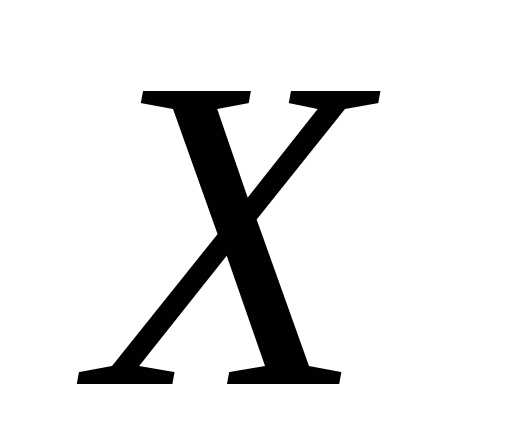 .
Пустьи
.
Пустьи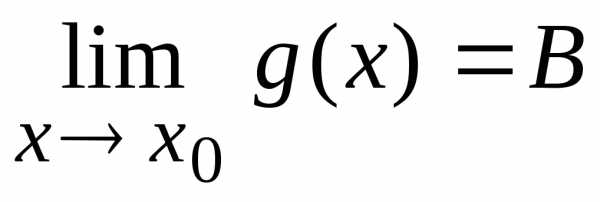 .
Тогда
.
Тогда
=;
=;
и,
если при любом 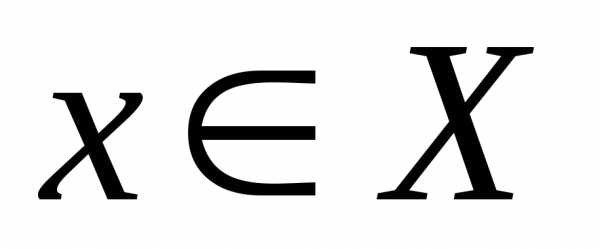
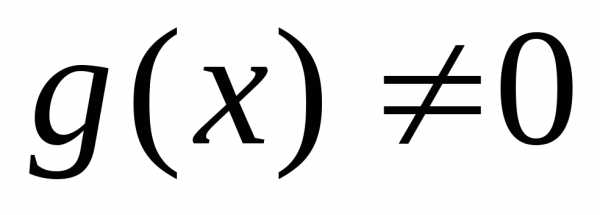
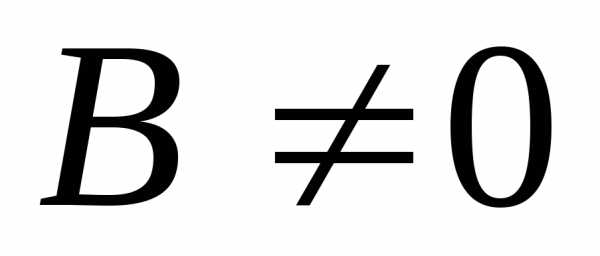 ,
то
,
то 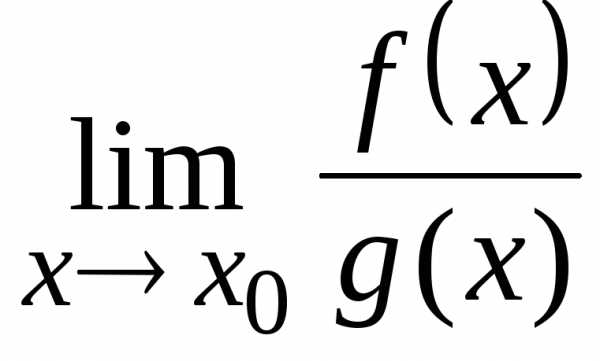 =
=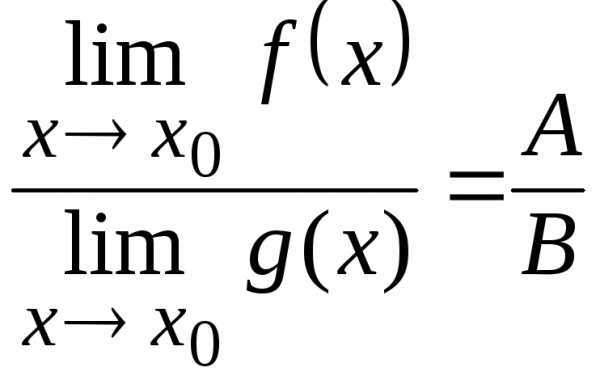 .
.
Доказательство. Ограничимся
рассмотрением случая отношения двух
функций. Выберем произвольно
последовательность 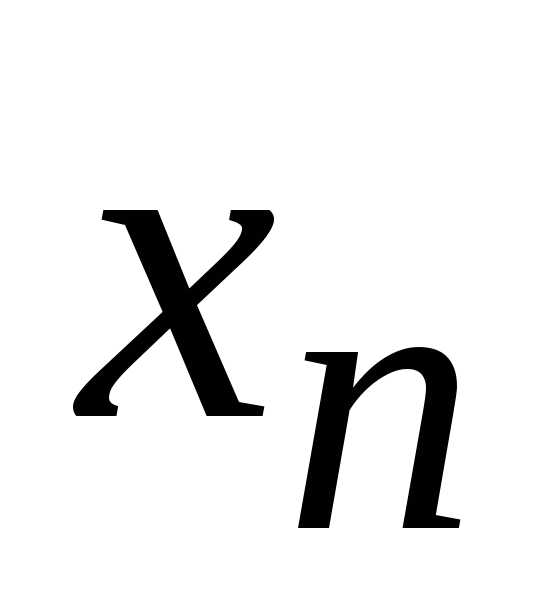 ,
,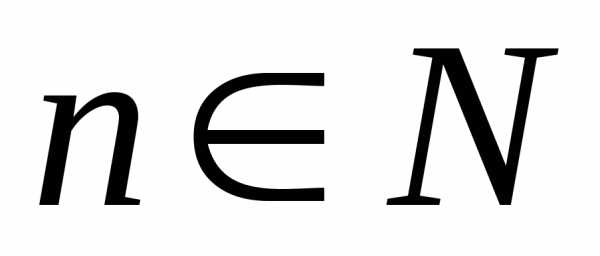 ,
для которой
,
для которой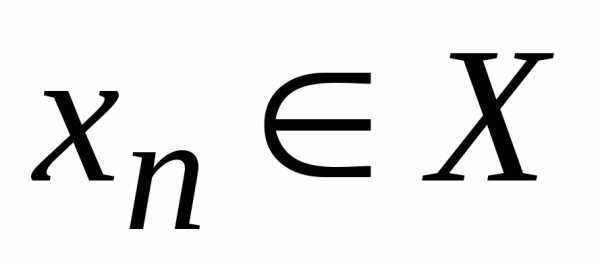 ,
,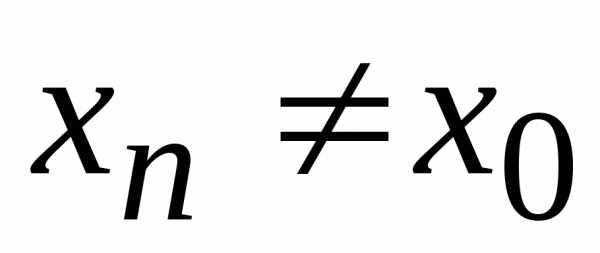 при любом
при любом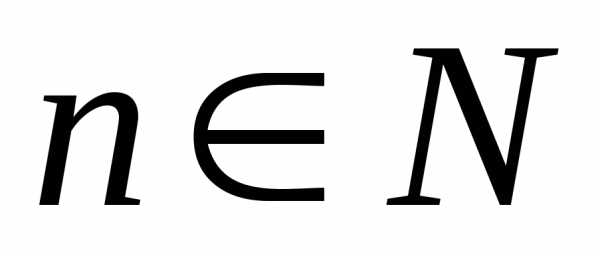 и
и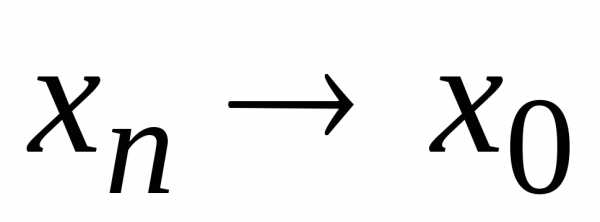 .
Тогда,и по теореме 3.12.
.
Тогда,и по теореме 3.12.
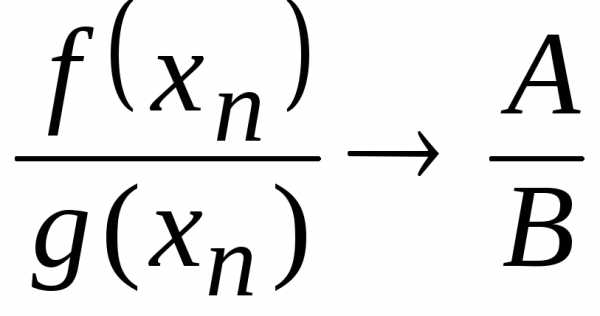 .
.
Теорема доказана.
4.4. Критерий Коши существования предела функции
Пусть 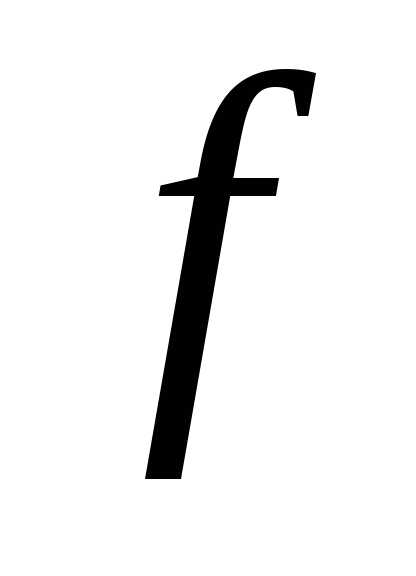 :
:
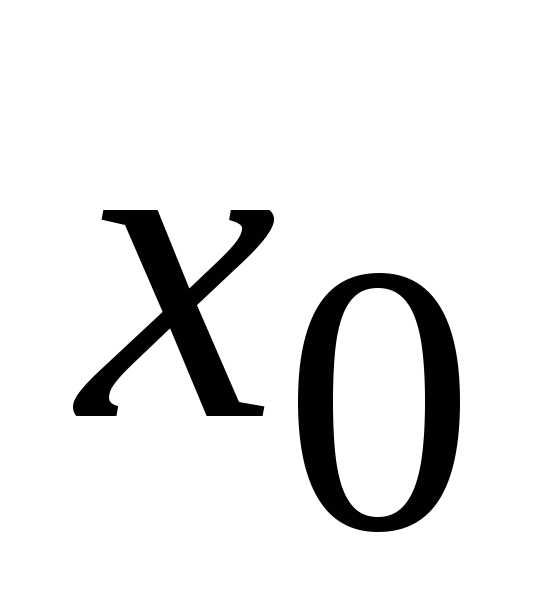 – предельная точка множества
– предельная точка множества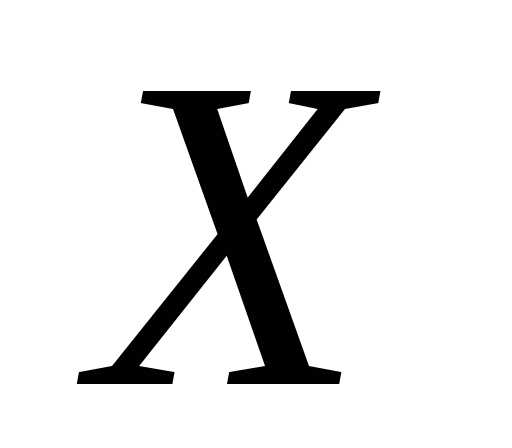 .
. Теорема
4.5. Для
того чтобы функция  имела конечный предел в точке
имела конечный предел в точке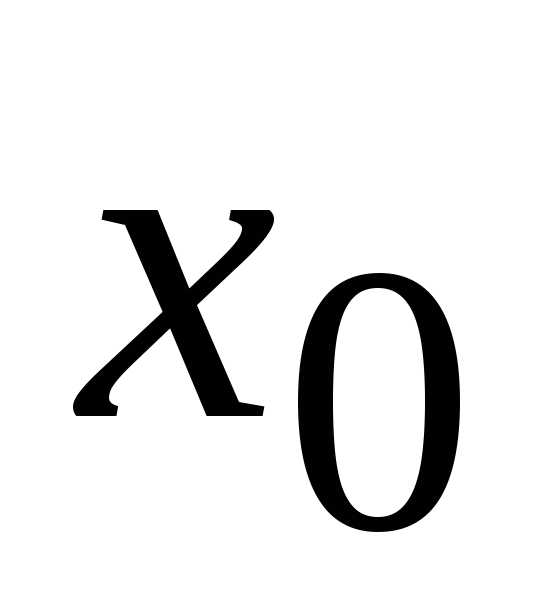 ,
необходимо и достаточно, чтобы выполнялось
условие Коши: для любого
,
необходимо и достаточно, чтобы выполнялось
условие Коши: для любого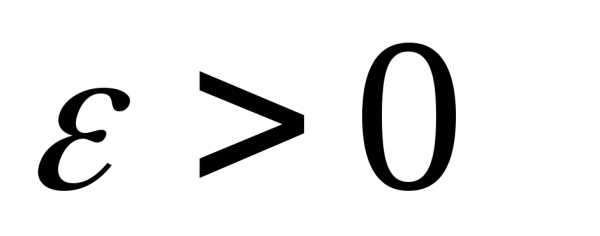 существовало
такое число
существовало
такое число ,
что для всех
,
что для всех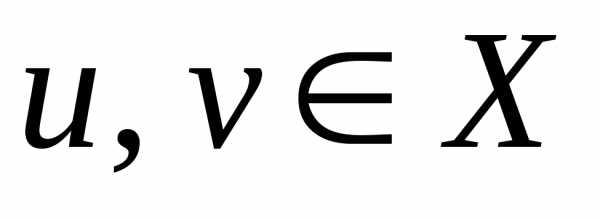 из неравенств,следует неравенство.
из неравенств,следует неравенство.
Доказательство. Необходимость. Пусть
.
Это означает, что для любого существует
такое число
существует
такое число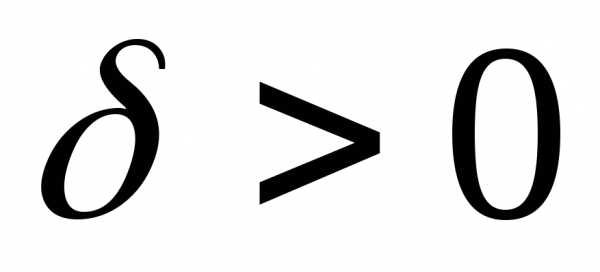 ,
что для любого
,
что для любого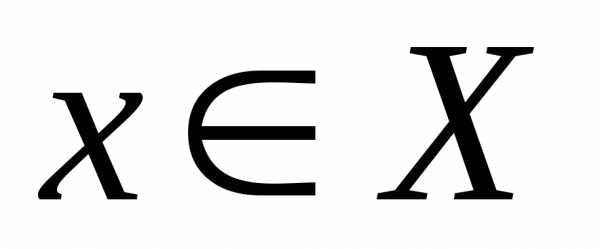 из неравенстввытекает неравенство.
Пусть
из неравенстввытекает неравенство.
Пусть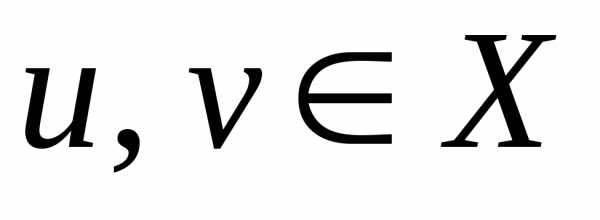 ,,,
тогда
,,,
тогда
.
Достаточность. Пусть выполнено условие Коши. Рассмотрим
последовательность 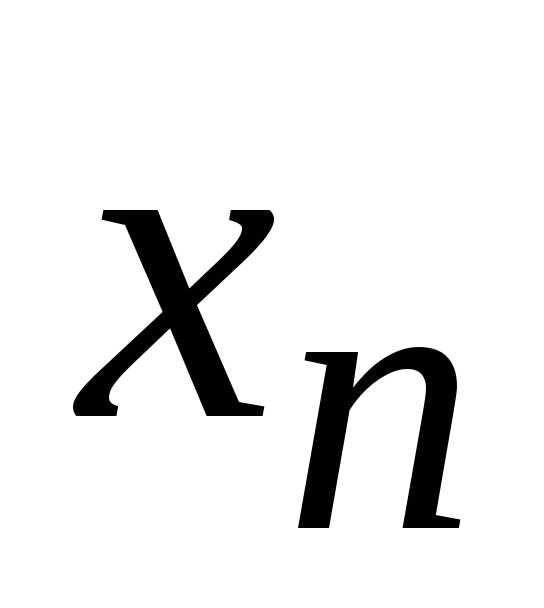 ,
,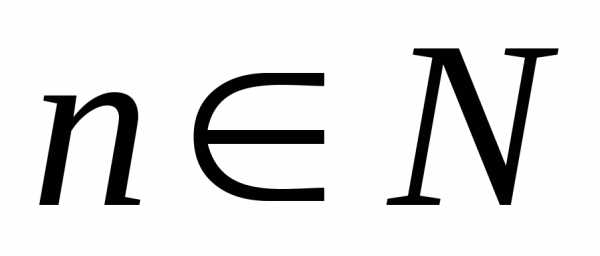 ,
для которой
,
для которой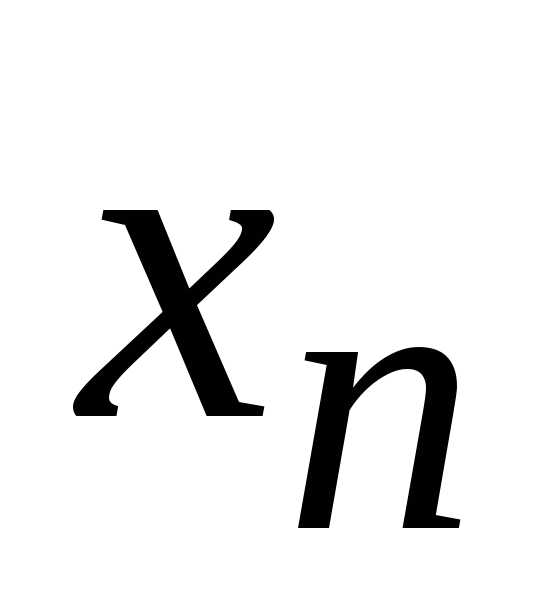
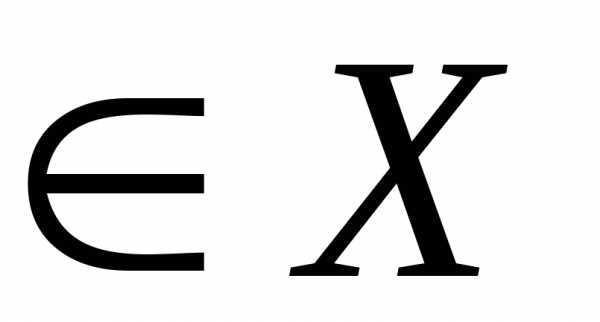 ,
,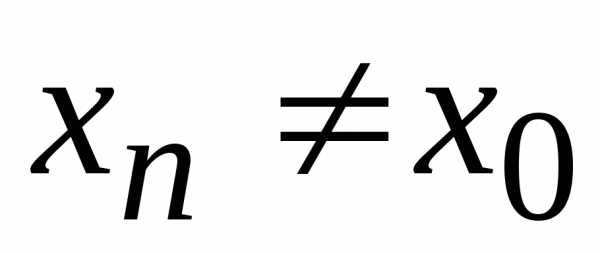 при любом
при любом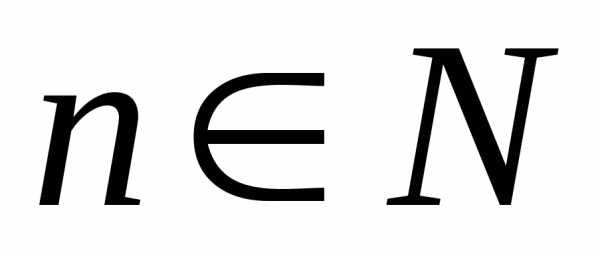 и
и .
.
Выберем
произвольно  и
рассмотрим
и
рассмотрим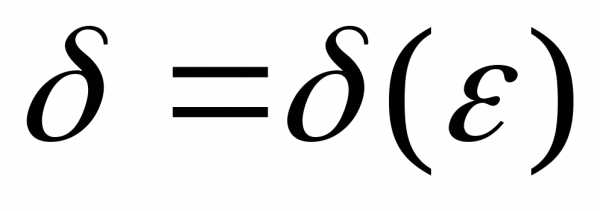 — число, фигурирующее в условии Коши.
Воспользуемся определением предела
последовательности
— число, фигурирующее в условии Коши.
Воспользуемся определением предела
последовательности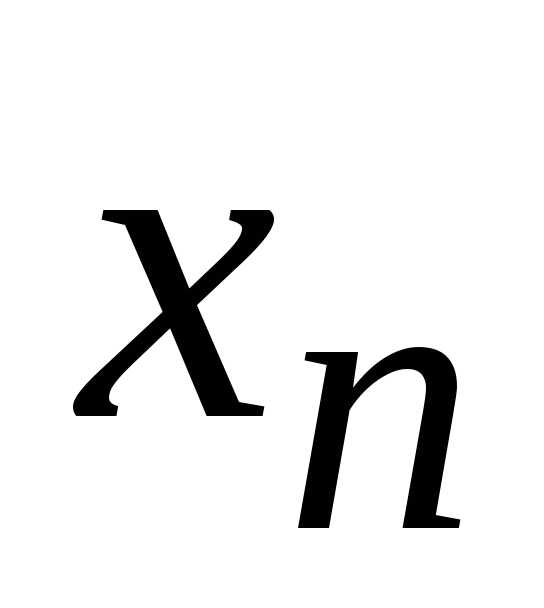 и обозначим через
и обозначим через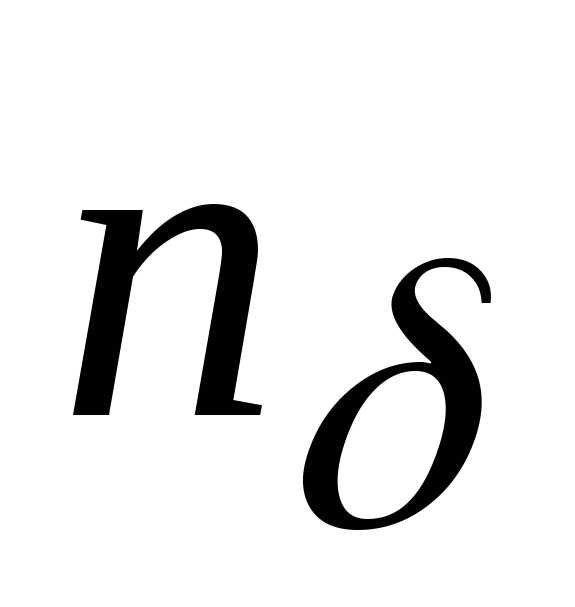 номер, начиная с которого выполняется
неравенство.
Пусть
номер, начиная с которого выполняется
неравенство.
Пусть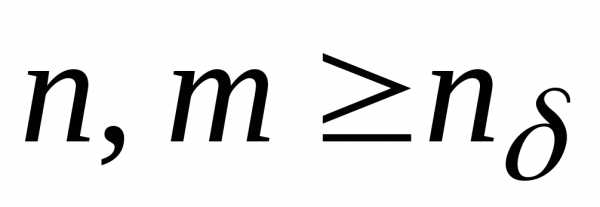 .
Тогда,и, по условию Коши,.
Это означает, что последовательность
.
Тогда,и, по условию Коши,.
Это означает, что последовательность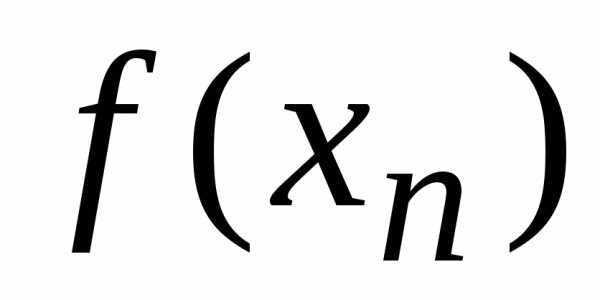 ,
,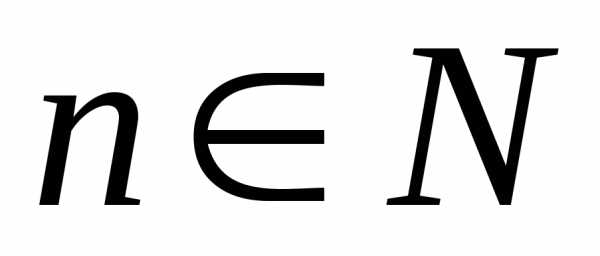 ,
фундаментальна и, в силу критерия Коши
для последовательностей, сходится.
,
фундаментальна и, в силу критерия Коши
для последовательностей, сходится.
Итак, мы показали, что для любой подходящей
последовательности 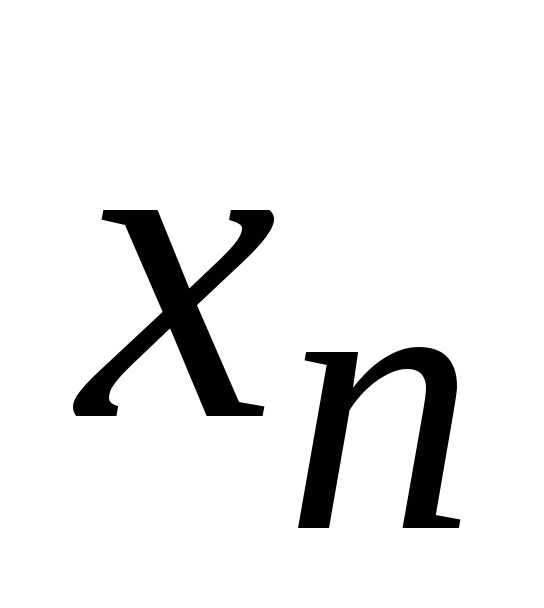 ,
,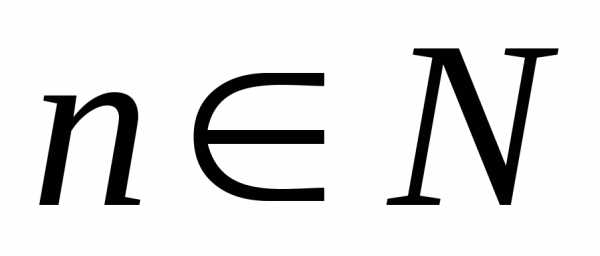 ,
соответствующая последовательность
,
соответствующая последовательность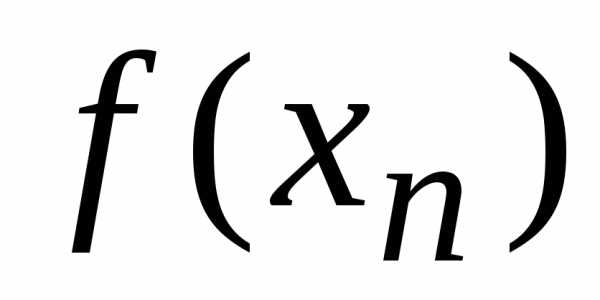 ,
,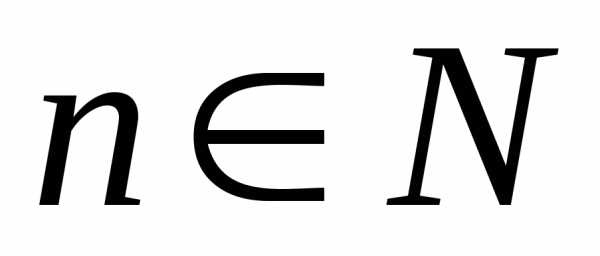 ,
сходится. Докажем, что предел
,
сходится. Докажем, что предел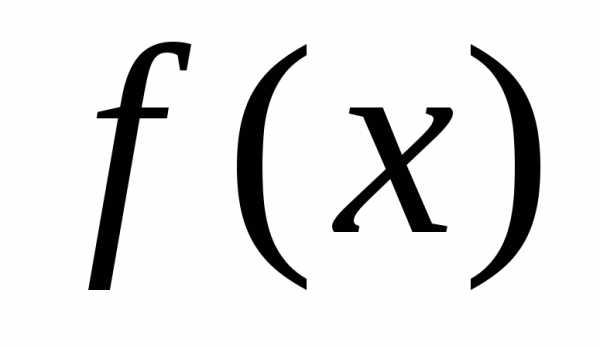 не зависит от выбора подходящей
последовательности.
не зависит от выбора подходящей
последовательности.
Пусть 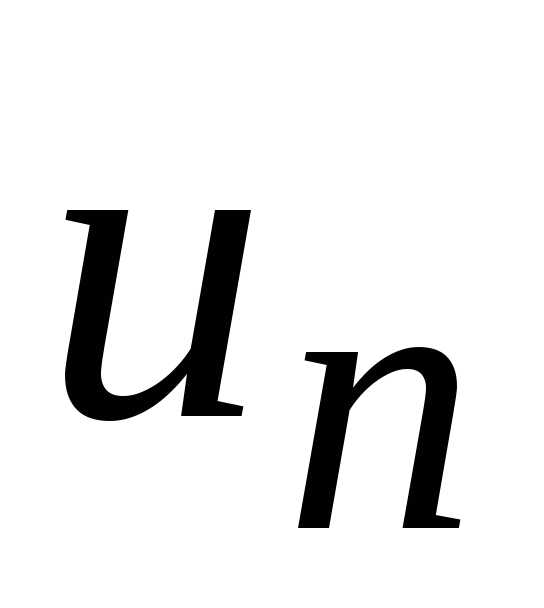 и
и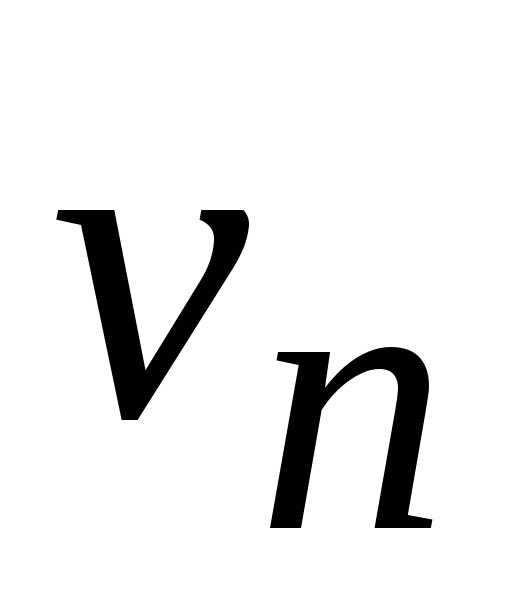 ,
,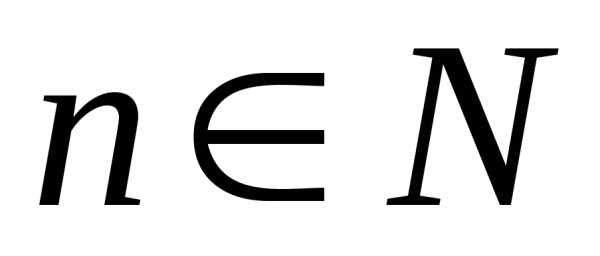 ,
— две подходящие последовательности.
Образуем из них новую последовательность
,
— две подходящие последовательности.
Образуем из них новую последовательность
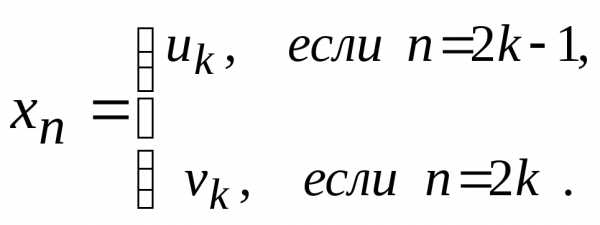
Эта
последовательность также сходится к 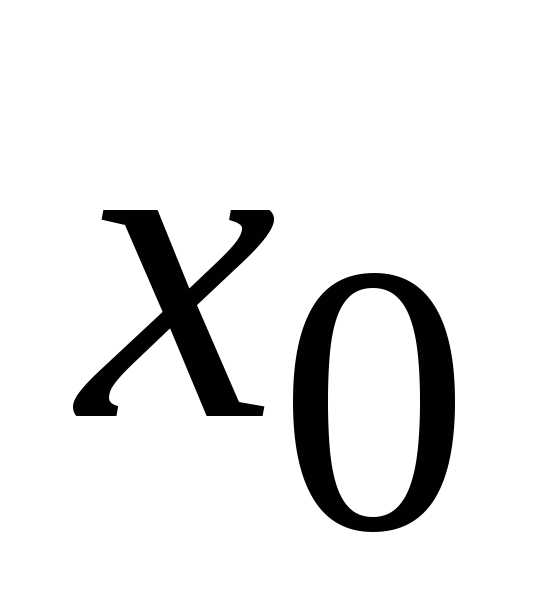 (см. задачу 3.15). Из доказанного выше
следует, что
(см. задачу 3.15). Из доказанного выше
следует, что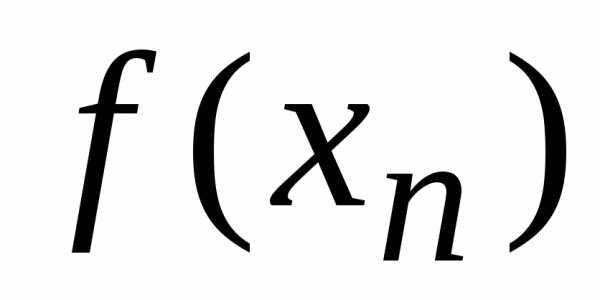 сходится, и поэтому последовательностииимеют одинаковые пределы.Теорема
доказана.
сходится, и поэтому последовательностииимеют одинаковые пределы.Теорема
доказана.
4.5. Расширение понятия предела. Односторонние пределы
Понятие
предела функции, приведенное в разделе
4.2, может быть расширено в различных
направлениях. Так, можно рассматривать,
к чему стремится функция при условии,
что либо
,
либо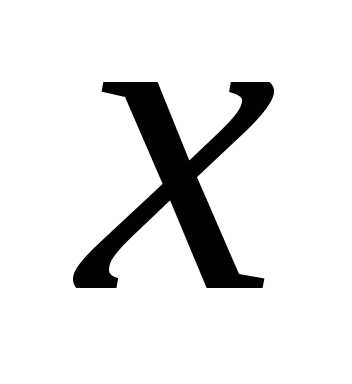 стремится к некоторому числу
стремится к некоторому числу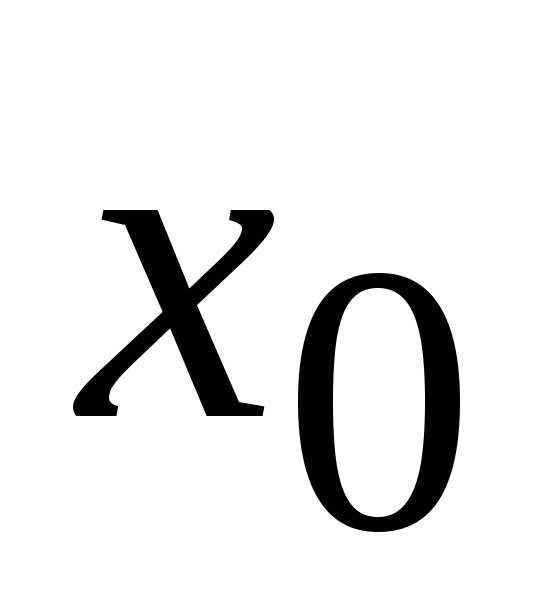 ,
оставаясь меньше этого числа, то есть
при.
Далее, можно предусмотреть, что функция
стремится к
,
оставаясь меньше этого числа, то есть
при.
Далее, можно предусмотреть, что функция
стремится к при том или ином поведении аргумента и
т.д. Возникающие таким образом варианты
предельного перехода можно записать в
общем виде:
при том или ином поведении аргумента и
т.д. Возникающие таким образом варианты
предельного перехода можно записать в
общем виде:
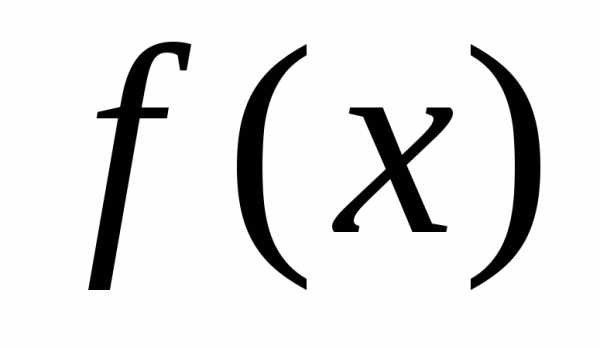 стремится
к
стремится
к 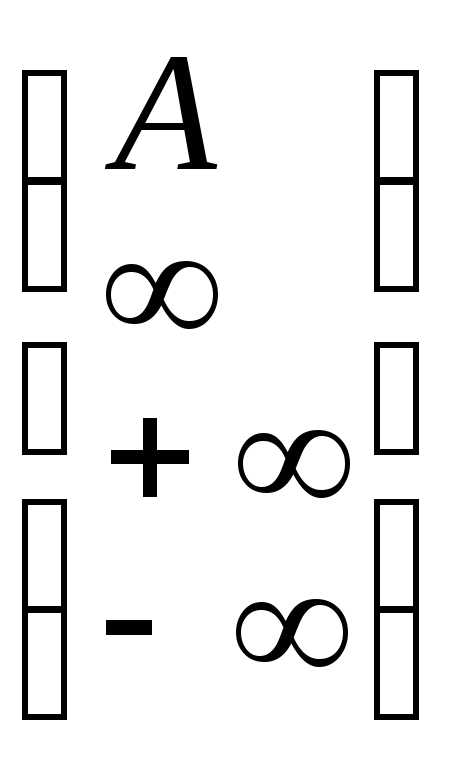 при
при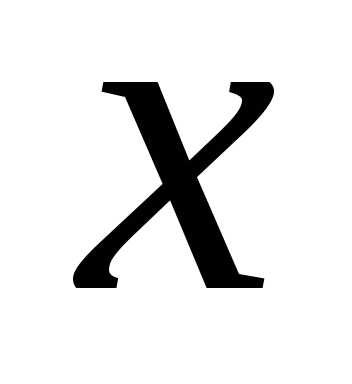 ,
стремящемся к
,
стремящемся к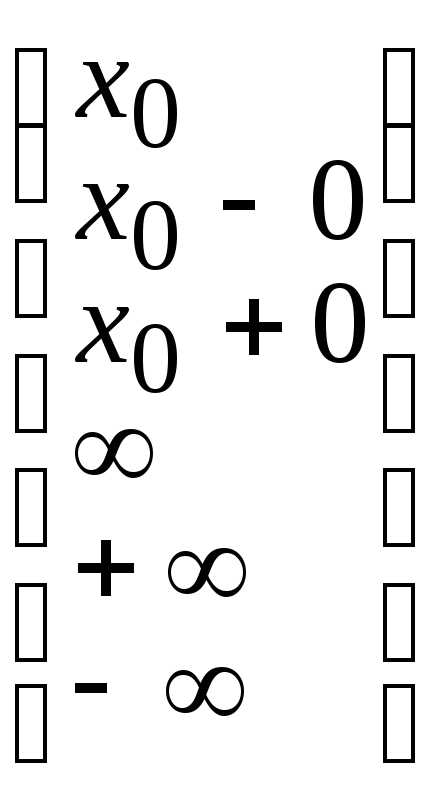 .
.
Выбирая
в каждом из двух столбцов по одному
символу, получим тот или иной из двадцати
четырех возможных вариантов. Для каждого
из них можно записать формальное
определение на языке “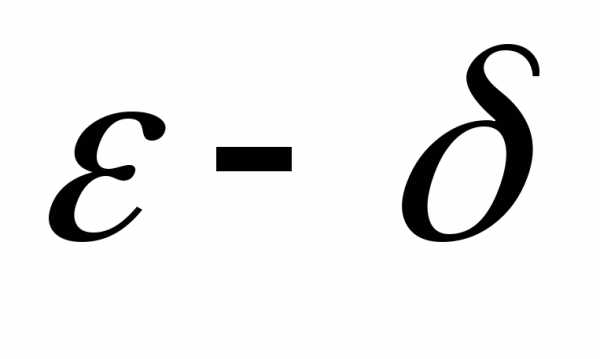 ”,
подобное определению 4.3 или на языке
последовательностей, подобное определению
4.4.
”,
подобное определению 4.3 или на языке
последовательностей, подобное определению
4.4.
Рассмотрим несколько случаев.
Пример 4.4.при.
Пусть
функция 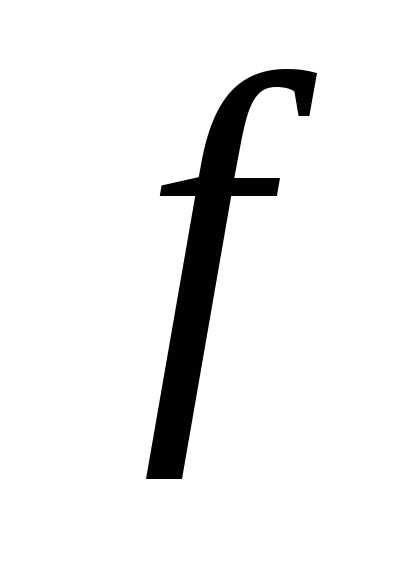 определена на неограниченном множестве
определена на неограниченном множестве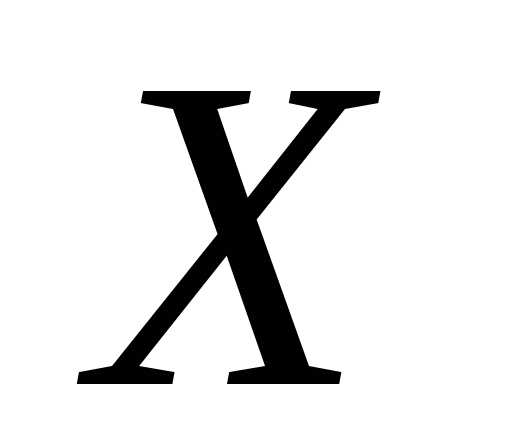 ,
и пустьA – некоторое
число. Тогда условие
,
и пустьA – некоторое
число. Тогда условие
в формальной записи имеет вид:
.
Или, на языке последовательностей,
.
Задача 4.2. Рассуждая аналогично доказательству теоремы 4.1, докажите эквивалентность определений, приведенных в примере 4.4.
Пример 4.5.при.
Пусть
функция 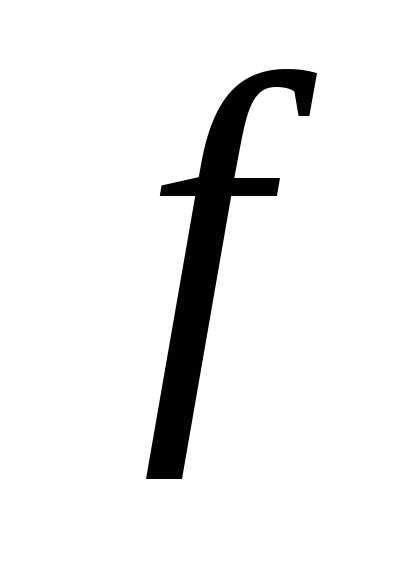 определена на множестве
определена на множестве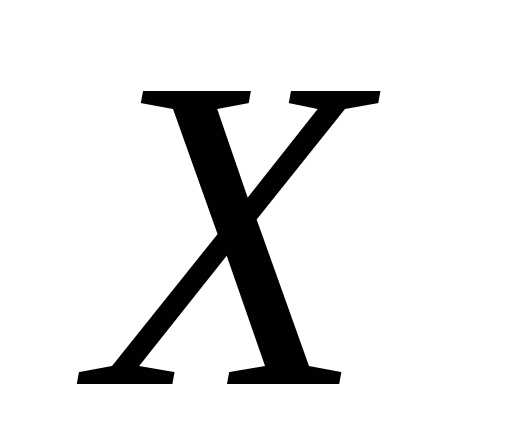 ,
и пусть точка
,
и пусть точка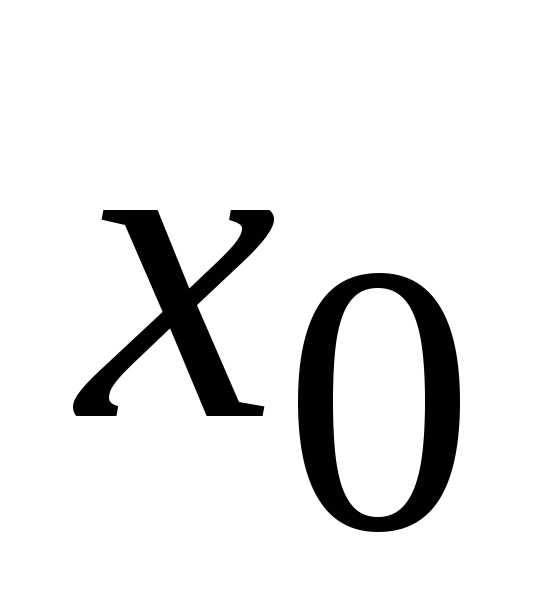 является предельной точкой множества
является предельной точкой множества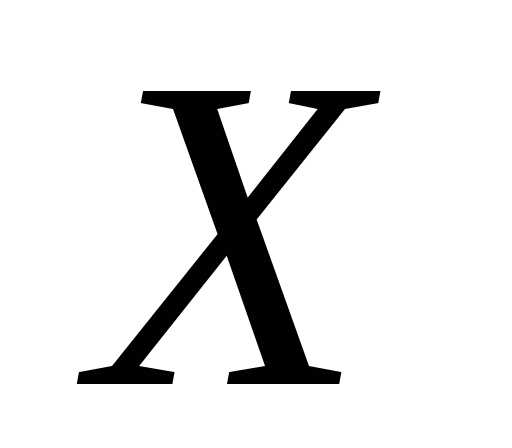 .
Пусть
.
Пусть
.
Тогда условие
на
языке “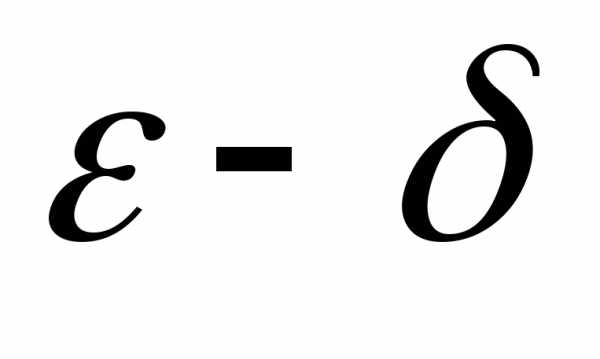 ”имеет вид:
”имеет вид:
,
а на языке последовательностей:
.
В
этом случае число  называется левосторонним пределом
функции
называется левосторонним пределом
функции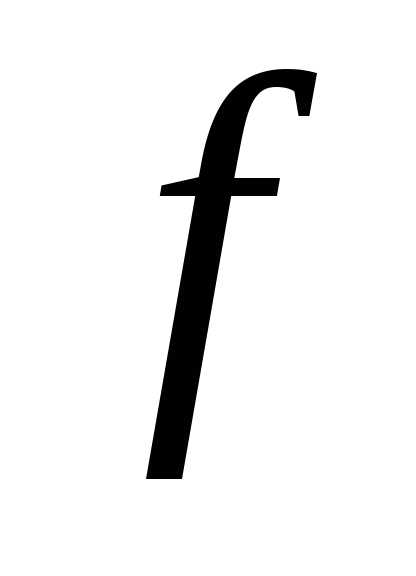 и обозначается
и обозначается
.
Аналогично
определяется правосторонний предел,
при этом вместо 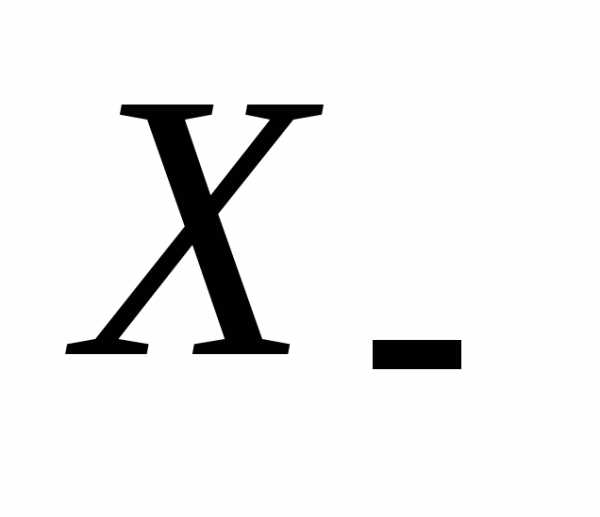 рассматривается.
рассматривается.
Теорема
4.6. Пусть функция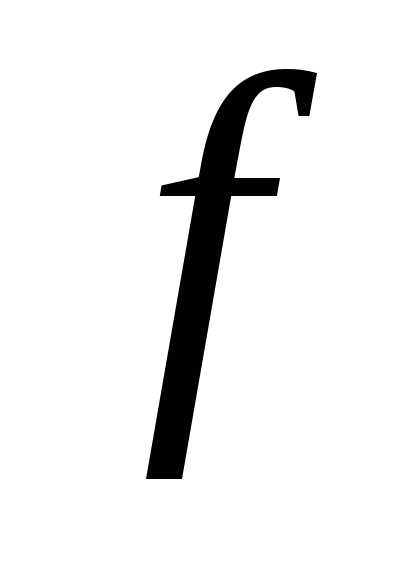 определена на множестве,
и пусть точка
определена на множестве,
и пусть точка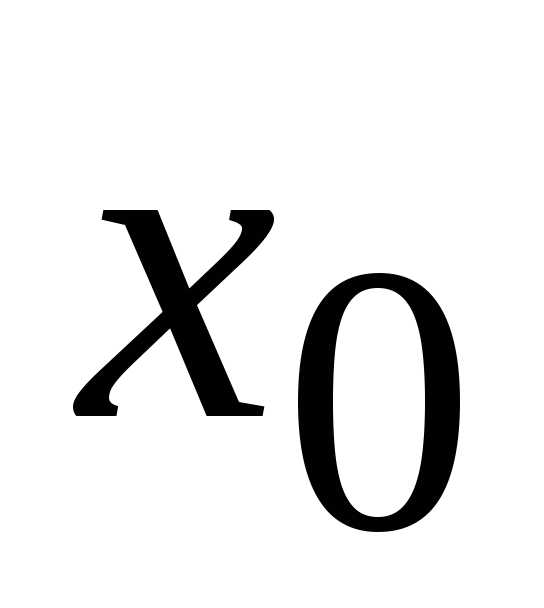 является предельной точкой множеств
является предельной точкой множеств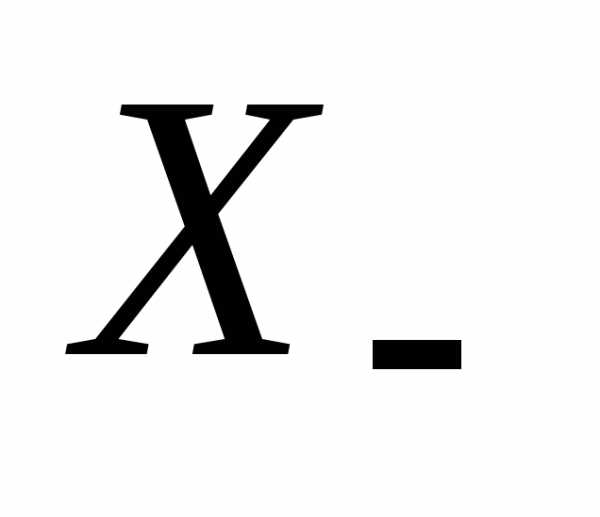 и
и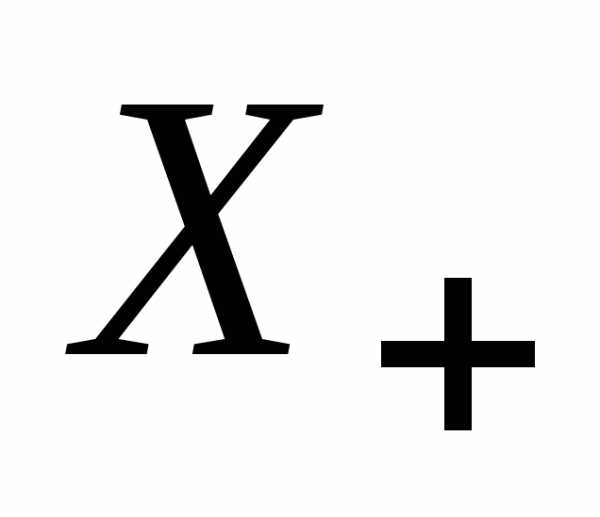 .
Тогда
.
Тогда
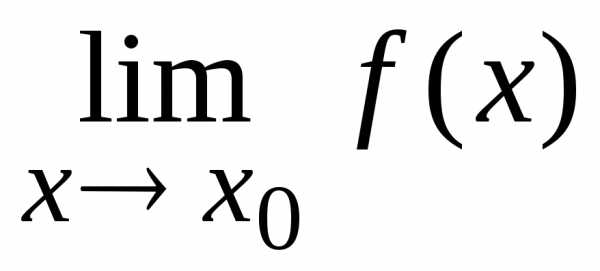 существует в том
и только в том случае, когда существуют
и равны между собой
существует в том
и только в том случае, когда существуют
и равны между собой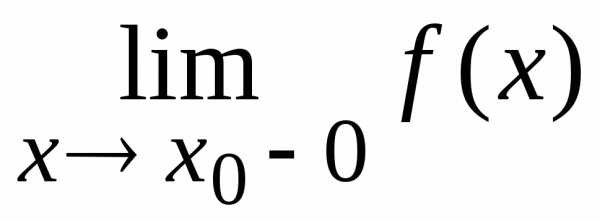 и
и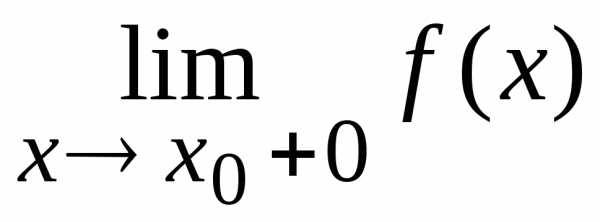 .
.
Задача 4.3. Докажите теорему 4.6.
studfiles.net
Предел функции в точке. Свойства предела. Односторонние пределы. Непрерывные функции и их свойства.
Числовой последовательностьюназывается занумерованное множество чисел, расположенных в порядке возрастания номеров.
В общем виде записывают: , где называется общим членом последовательности.
Последовательность называется возрастающей,( убывающей) если каждый ее член начиная со второго, больше (больше или равен) предыдущего, т.е. если для любого n выполняется неравенство: .( )
Переменная величина называется бесконечно малой, если она изменяется так, что, какое бы малое положительное число ни взять, абсолютная величина становится, и, при дальнейшем изменении величины , остается, меньше .
Если — бесконечно большая величина, то обратная ей величина будет бесконечно малой.
Если — бесконечно малая величина, то обратная ей величина будет бесконечно большой.
Постоянная называется пределом переменной х , если х в некотором процессе стремится к конечному пределу и безгранично приближается к . Тогда пишут или .
Число называется пределом последовательности , если для любого положительного числа можно подобрать такой номер N0, что начиная с этого номера ( т.е. для всех n N0), будет выполнено неравенство:
( )
Если последовательность имеет конечный предел, то она называется сходящейся, если не имеет конечного предела, тогда расходящейся.
Свойства пределов:
1. Если последовательность имеет конечный предел, то только один.
2. Предел постоянной величины равен ей самой:
3. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) их пределов: .
4. Предел произведения двух сходящихся последовательностей равен произведению их пределов:
5. Постоянный множитель можно выносить за знак предела: ( )
6. Предел частного двух сходящихся последовательностей равен частному их пределов:
( )
7. Предел корня k-ой степени от сходящейся последовате6льности равен корню этой же степени от предела последовательности:
Важно знать некоторые пределы:
1. , где — второй замечательный предел
2.
3.
Определение предела функции по Гейне:
Число А называется пределом функции при стремящимся к , если для любой последовательности , все члены которой принадлежат области определения функции и не равны выполняется условие что последовательность стремится к А.
)
Определение предела функции по Коши:
Число А называется пределом функции при , если для любого числа можно указать такое , что для всех , удовлетворяющего неравенству , выполняется неравенство .
В этом случае пишут .
Если число А1 есть предел функции при х, стремящемся к а, так, что х принимает только значения, меньшие а, то А1 называется левым пределом функции в точке а. При этом пишут .
Если число А2 есть предел функции при х, стремящемся к а, так, что х принимает только значения, большие а, то А2 называется правым пределом функции в точке а. При этом пишут .
Эти пределы называются односторонними пределами функции.
Теорема: Для того, чтобы функция имела предел равный А в точке а, необходимо и
Достаточно, чтобы существовали односторонние пределы функции в этой точке и
были равны между собой.
Теорема 1: Если существуют конечные пределы функций и при , то существует
предел их суммы (разности), равный сумме (разности) пределов функций и :
Теорема 2: Если существуют конечные пределы функций и при , то существует
предел их произведения, равный произведению пределов функций и :
Теорема 3: Если существуют конечные пределы функций и при , то существует
предел отношения , равный отношению пределов функций и :
, где
Следствия:
1. Постоянный множитель можно вынести за знак предела: , .
2. Если — натуральное число, то , при .
3. Предел многочлена при равен значению этого многочлена при т.е. .
4. Предел дробно-рациональной функции при равен значению этой функции при , если принадлежит области определения функции, т.е. и .
Важно знать некоторые пределы наизусть:
Первый замечательный предел—
Следствия:
Второй замечательный предел —
Следствия:
Функция называется непрерывной в точке если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Функция называется непрерывной в точке , если для любого существует , такое, что для всех из области определения функции, удовлетворяющих условию ,выполняется неравенство .
Функция называется непрерывной в точке , если предел функции в этой точке существует и равен значению функции в этой точке.
Условия непрерывности функции в точке:
1. — определена.
2.
3.
Теорема 1: Если функции и непрерывны в точке , то функция так же
непрерывна в этой точке.
Теорема 2: Если функции и непрерывны в точке , то функция так же
непрерывна в этой точке.
Теорема 3: Если функции и непрерывны в точке и , то функция
так же непрерывна в этой точке.
Свойства функций непрерывных на отрезке.
Теорема1: Больцано- Вейерштрасса об ограниченности непрерывной функции.
Если функция определена и непрерывна на отрезке , то она ограничена на этом отрезке.
Теорема2: Больцано- Вейерштрасса о достижении верхней и нижней граней
Если функция определена и непрерывна на отрезке . Тогда эта функция принимает на отрезке свои наибольшие и наименьшие значения, т.е. существуют такие точки , что для любой точки справедливы равенства .
Теорема3: Больцано- Коши о нулях непрерывной функции
Если функция определена и непрерывна на отрезке и на концах его принимает значения противоположных знаков, то существует точка на этом отрезке в которой значение функции равно нулю .
Теорема4: Больцано- Коши о промежуточных значениях непрерывной функции
Если функция определена и непрерывна на отрезке . Тогда для любого числа С, заключенного между числами и , найдется такая точка , что
Если не является непрерывной в точке , то точка называется точкой разрыва функции.
Условие непрерывности можно переписать следующим образом: (*)
Если хотя бы одно из выражений в равенстве (*) не существует или не выполняется хотя бы одно из равенств, то точка называется точкой разрыва функции.
Точка называется точкой разрыва устранимого режима, если односторонние пределы функции в этой точке существуют и равны между собой, но не равны значению функции в этой точке или функция в этой точке не определена.
У у
0 х0 х 0 х0 х
Точка называется точкой разрыва первого рода (скачок), если односторонние пределы функции в этой точке существуют но не равны между собой.
у
0 х0 х
Точка называется точкой разрыва второго рода, если хотя бы один из односторонних пределов функции в этой точке не существует или равен бесконечности.
у
0 х0 х
Теорема: Если строго монотонна на и произвольная точка этого отрезка, то
верхняя грань совпадает с левым пределом этой функции, не превосходит , не
превосходит правого предела и не превосходит правой грани.
Утверждение1: Всякая строго монотонная на промежутке функция имеет односторонние пределы в
каждой точке этого промежутка.
Утверждение2: Если односторонние пределы строго монотонной функции в точке совпадают, то
функция непрерывна в этой точке.
Утверждение3: Если односторонние пределы строго монотонной функции в точке не совпадают, то
это точка разрыва первого рода (скачок).
Тема 2.2. Лекция 9. Занятие 13
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Предел функции.Определения. Свойства предела
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Преде́л фу́нкции— одно из основных понятий математического анализа. Функцияf(x) имеет пределAв точкеx0если для всех значенийx, достаточно близких кx0, значениеf(x) близко кA.
Определения
(определение по Коши, ε−δ—определение) Пусть дана функция и— предельная точка множестваM. Числоназывается пределом функцииfприx, стремящемся кa, если
при
Замечания
Все данные выше определения предела функции в точке эквивалентны.
Если предел функции fприсуществует и равенA, пишут
Предел вдоль фильтра
Определение фильтра
Основная статья:Фильтр (математика)
Пусть дано множество A. Система множествназывается фильтром наA, если
Определение предела
Пусть и— фильтр наM. Числоявляется пределом функцииfпо фильтруесли
Пишут:
Примеры
Обычный предел
Пусть дано топологическое пространство , иПустьТогда система множеств
является фильтром и обозначается Данное выше определение предела совпадает с пределом по фильтру
Односторонние пределы
Основная статья:Односторонние пределы
является фильтром и обозначается илиПределназывается правосторонним пределом функцииfприxстремящемся кa.
является фильтром и обозначается илиПределназывается левосторонним пределом функцииfприxстремящемся кa.
Пределы на бесконечности
Основная статья:Пределы функции на бесконечности
является фильтром и обозначается илиПределназывается пределом функцииfприxстремящемся к бесконечности.
является фильтром и обозначается Пределназывается пределом функцииfприxстремящемся к минус-бесконечности.
Предел последовательности
Основная статья:Предел последовательности
Система множеств где
является фильтром и обозначается Функцияназывается числовой последовательностью, а пределпределом этой последовательности.
Интеграл Римана
Основная статья:Интеграл Римана
Пусть Назовём размеченным разбиением отрезка [a,b] коллекцию точекНазовём диаметром разбиенияTчислоТогда система множеств
является фильтром в пространстве всех размеченных разбиений [a,b]. Определим функциюравенством
Тогда предел называется интегралом Римана функцииfна отрезке [a,b].
Свойства пределов числовых функций
Пусть даны функции иТогда
где — проколотая окрестность точкиa.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
studfiles.net
