Урок «Объём куба» 3 класс
Открытый урок-исследование по математике в 3 классе.
Тема: Объем куба и параллелепипеда.
Цель: ●Познакомить с измерением объема и единицами объема:1см³, 1дм³, 1м³.
● Выведение формулы объема прямоугольного параллелепипеда и куба.
● Развитие исследовательских, мыслительных, социальных навыков.
Оборудование: Модели геометрических фигур — куба, параллелепипеда, пирамиды;
кубики, схема «Величина», опорная таблица для вычисления объема.
Ход урока.
Сообщение темы, целей урока.
( на доске критерии успеха).
Ваша работа будет успешной, если вы:
● покажете знания изученных величин и единиц их измерения.
● будете активно участвовать в исследовании, выражать собственное мнение и давать высказываться другим.
●ваша деятельность на уроке покажет, что вы понимаете, что такое объем и можете его вычислить.
● сможете вывести формулу объема куба и прямоугольного параллелепипеда.
Навыки: исследовательские, мыслительные, социальные, навыки общения (коммуникативные)
1. Прочитай запись на доске: 34 дм, 12кг, 5л, 7м²
-Как назвать эти именованные числа одним словом? (величины).
— Что мы называем величиной?
(Величина-это то, что можно измерить и, результат измерения, выразить числом).
-Какие величины выражают данные именованные числа?
(длина, масса, объем, площадь).
а) – Работа, которую вы сейчас выполните, развивает очень важные для вас исследовательские навыки; такие как классификация данных и умение работать в группе.
— Возьмите схему «Величина», заполните её, обозначив единицы измерения данных величин.
ВЕЛИЧИНА
ДЛИНА МАССА ОБЪЕМ ПЛОЩАДЬ
мм см дм м км г кг ц т л □ см² дм² м² км²
— Осталось ли свободное окошко?
— Сегодня на уроке мы узнаем, какие ещё существуют единицы измерения объёма.
б) (на доске рисунки плоских и объемных фигур: прямоугольник, треугольник, квадрат, куб, параллелепипед)
Какие виды фигур перед вами? (плоские, объёмные)
— Как называется каждая фигура?
— Чем они отличаются? (плоские: длина, ширина; объёмные: длина, ширина, высота)
— Какими единицами измерения можно определить величины этих фигур?
2. Для того, чтобы говорить об объёме фигуры, нужно ещё раз вспомнить известную нам единицу измерения объёма (литр).
Для чего она используется? (для измерения объёма жидкости и вместимости сосудов).
-Существуют и другие единицы измерения объёма. Это — см³, дм³, м³.
(показать). Кубик с ребром 1см называется см³, с ребром 1 дм — дм³, с ребром 1м- м³ (показать грань).
(На доске изображены фигуры, составленные из кубов)
-Сколько кубиков в каждой из фигур?
— Что можно сказать об объёме данных фигур?
(их объём равен 4см³, 6см³, 8см³)
-Как вы думаете, почему взяли именно кубик в качестве мерки?
(ребра куба равны между собой)
Расшифровав слово, вы узнаете, о какой фигуре пойдет сейчас речь?
(цифры поставить в порядке возрастания).
П 18:9=2 Л (28+12):4=10
Е (28-23)•6=30 П 90-45:9=85
Р (20-6):2=7 А 100:(32-12)=5
А 32:4=8
И 5•5•3=75 П 56:8•10=70
Е 500:50•10=100 Д 1000-(20•30)=400
Л 3•(18:2)27 Е (24+16):2=20
Л 56:7•2=16
2,5,7,8,10,16,20,27,30,70,75,85,100,400.
(параллелепипед)
3. Для того, чтобы вывести формулу куба и прямоугольного параллелепипеда, мы проведем наше исследование через следующие концепции:
А. Форма и связь:
Что общего между кубом и параллелепипедом?
(в группах рассматривают фигуры, делают выводы)
●Объёмные фигуры с прямыми углами.
● Одинаковое количество граней, вершин, ребер.
● Есть три измерения: длина, ширина, высота.
Б. Изменение, причинность. ( Работа в группах).
— Постройте из кубиков модель куба.
Что можно сказать о его трех измерениях?
(равны)
Внесите изменения так, чтобы из куба получился параллелепипед.
Проведите измерения.
Что можно сказать о трех измерениях параллелепипеда?
(длина, высота, ширина не равны).
В. Размышление:
Сейчас каждая группа проводит исследование, проведя необходимые построения и
выполнив вычисления.
Задание: Используя три измерения: длину, ширину и высоту параллелепипеда, вычислить его объём. Данные и вывод записываются в опорной таблице: (1 кубик считается как 1см³)
● На основании стоит____________ кубиков.
●S основания (дна) параллелепипеда равна ____________ см²
● По высоте параллелепипеда выложили _______________ таких слоя.
● Объём равен ( □ • □ ) • □ = □ см³
S осн. • высота
Выведение формулы:
записать этот вывод в виде формулы?
(V=a • b • c).
— А как будет выглядеть формула нахождения объёма куба
(V= a • a • a)
Самооценка.
(лист самооценки). Приложение №2.
Следующий урок мы посвятим составлению и решению задач по формулам, выведенным сегодня на уроке.
Приложение №2.
ЛИСТ САМООЦЕНКИ.
Деятельность: студенты выводят формулу объёма куба и прямоугольного параллелепипеда.
Мои размышления.
1. Больше всего мне на уроке понравилось ______________________________________
2. Мне трудно было ________________________________________________________
__________________________________________________________________________
3. Теперь я знаю, что для нахождения объёма фигуры нужно знать её _______________
Формула объёма куба________________________________________________________
Формула объёма прямоугольного параллелепипеда ______________________________
В работе я использовал следующие навыки:
Всегда Иногда Редко
Мыслительные
Исследовательские
Коммуникативные
Социальные
Свою работу на уроке я оцениваю так:
1. Отлично
2. Хорошо
3. Мне нужно постараться
infourok.ru
Открытый урок 3 класс «Объем куба и параллелепипеда» — Математика — В помощь учителю — Учительские университеты
Открытый урок-исследование по математике в 3 классе.Тема: Объем куба и параллелепипеда.
Цель: ●Познакомить с измерением объема и единицами объема:1см³, 1дм³, 1м³.
● Выведение формулы объема прямоугольного параллелепипеда и куба.
● Развитие исследовательских, мыслительных, социальных навыков.
Оборудование: Модели геометрических фигур — куба, параллелепипеда, пирамиды;
кубики, схема «Величина», опорная таблица для вычисления объема.
Ход урока.
Сообщение темы, целей урока.
( на доске критерии успеха).
Ваша работа будет успешной, если вы:
● покажете знания изученных величин и единиц их измерения.
● будете активно участвовать в исследовании, выражать собственное мнение и давать высказываться другим.
●ваша деятельность на уроке покажет, что вы понимаете, что такое объем и можете его вычислить.
● сможете вывести формулу объема куба и прямоугольного параллелепипеда.
Навыки: исследовательские, мыслительные, социальные, навыки общения (коммуникативные)
1. Прочитай запись на доске: 34 дм, 12кг, 5л, 7м²
-Как назвать эти именованные числа одним словом? (величины).
— Что мы называем величиной?
(Величина-это то, что можно измерить и, результат измерения, выразить числом).
-Какие величины выражают данные именованные числа?
(длина, масса, объем, площадь).
а) – Работа, которую вы сейчас выполните, развивает очень важные для вас исследовательские навыки; такие как классификация данных и умение работать в группе.
— Возьмите схему «Величина», заполните её, обозначив единицы измерения данных величин.
ВЕЛИЧИНА
ДЛИНА МАССА ОБЪЕМ ПЛОЩАДЬ
мм см дм м км г кг ц т л □ см² дм² м² км²
— Осталось ли свободное окошко?
— Сегодня на уроке мы узнаем, какие ещё существуют единицы измерения объёма.
б) (на доске рисунки плоских и объемных фигур: прямоугольник, треугольник, квадрат, куб, параллелепипед)
Какие виды фигур перед вами? (плоские, объёмные)
— Как называется каждая фигура?
— Чем они отличаются? (плоские: длина, ширина; объёмные: длина, ширина, высота)
— Какими единицами измерения можно определить величины этих фигур?
2. Для того, чтобы говорить об объёме фигуры, нужно ещё раз вспомнить известную нам единицу измерения объёма (литр).
Для чего она используется? (для измерения объёма жидкости и вместимости сосудов).
-Существуют и другие единицы измерения объёма. Это — см³, дм³, м³.
(показать). Кубик с ребром 1см называется см³, с ребром 1 дм — дм³, с ребром 1м- м³ (показать грань).
(На доске изображены фигуры, составленные из кубов)
-Сколько кубиков в каждой из фигур?
— Что можно сказать об объёме данных фигур?
(их объём равен 4см³, 6см³, 8см³)
-Как вы думаете, почему взяли именно кубик в качестве мерки?
(ребра куба равны между собой)
Расшифровав слово, вы узнаете, о какой фигуре пойдет сейчас речь?
(цифры поставить в порядке возрастания).
П 18:9=2 Л (28+12):4=10
Е (28-23)•6=30 П 90-45:9=85
Р (20-6):2=7 А 100:(32-12)=5
А 32:4=8
И 5•5•3=75 П 56:8•10=70
Е 500:50•10=100 Д 1000-(20•30)=400
Л 3•(18:2)27 Е (24+16):2=20
Л 56:7•2=16
2,5,7,8,10,16,20,27,30,70,75,85,100,400.
(параллелепипед)
3. Для того, чтобы вывести формулу куба и прямоугольного параллелепипеда, мы проведем наше исследование через следующие концепции:
А. Форма и связь:
Что общего между кубом и параллелепипедом?
(в группах рассматривают фигуры, делают выводы)
●Объёмные фигуры с прямыми углами.
● Одинаковое количество граней, вершин, ребер.
● Есть три измерения: длина, ширина, высота.
Б. Изменение, причинность. ( Работа в группах).
— Постройте из кубиков модель куба.
Что можно сказать о его трех измерениях?
(равны)
Внесите изменения так, чтобы из куба получился параллелепипед.
Проведите измерения.
Что можно сказать о трех измерениях параллелепипеда?
(длина, высота, ширина не равны).
В. Размышление:
Сейчас каждая группа проводит исследование, проведя необходимые построения и
выполнив вычисления.
Задание: Используя три измерения: длину, ширину и высоту параллелепипеда, вычислить его объём. Данные и вывод записываются в опорной таблице: (1 кубик считается как 1см³)
● На основании стоит____________ кубиков.
●S основания (дна) параллелепипеда равна ____________ см²
● По высоте параллелепипеда выложили _______________ таких слоя.
● Объём равен ( □ • □ ) • □ = □ см³
S осн. • высота
Выведение формулы:
— Если три измерения обозначит буквами a, b, c, а объём буквой V, то как можно
записать этот вывод в виде формулы?
(V=a • b • c).
— А как будет выглядеть формула нахождения объёма куба
(V= a • a • a)
Самооценка.
(лист самооценки). Приложение №2.
Следующий урок мы посвятим составлению и решению задач по формулам, выведенным сегодня на уроке.
Приложение №2.
ЛИСТ САМООЦЕНКИ.
Деятельность: студенты выводят формулу объёма куба и прямоугольного параллелепипеда.
Мои размышления.
1. Больше всего мне на уроке понравилось ______________________________________
2. Мне трудно было ________________________________________________________
__________________________________________________________________________
3. Теперь я знаю, что для нахождения объёма фигуры нужно знать её _______________
Формула объёма куба________________________________________________________
Формула объёма прямоугольного параллелепипеда ______________________________
В работе я использовал следующие навыки:
Всегда Иногда Редко
Мыслительные
Исследовательские
Коммуникативные
Социальные
Свою работу на уроке я оцениваю так:
1. Отлично
2. Хорошо
3. Мне нужно постараться
collegy.ucoz.ru
Расчет объема куба
Куб это геометрическое тело, ограниченное шестью квадратами, которое ещё можно назвать правильный шестигранник, а так же правильный многогранник. Слово «куб» образовано от греческого слова «kybos».
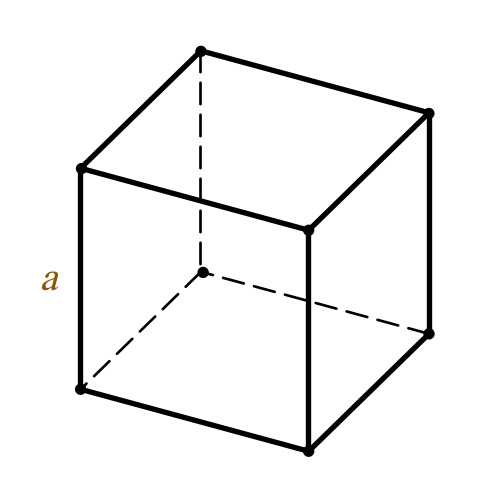
Определение объема куба
Расчет объема куба можно произвести с помощью следующей формулы:
V = a3
a – сторона куба
V – объем куба
Куб представляет собой правильный многогранник, каждая из граней которого является квадратом. Это геометрическое тело является частным случаем других (а именно – параллелепипеда и призмы) и в повседневной жизни встречается достаточно часто. Инженерам и архитекторам при разработке проектов различных машин и зданий нередко приходится производить расчет объема куба, причем ввиду относительной его простоты решение этой задачи обычно не представляет большой сложности.
На практике с кубами и параллелепипедами чаще всего приходится встречаться в архитектуре. Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.
Форму куба нередко имеют различные предметы корпусной мебели, и при их разработке конструкторам требуется определять, в том числе, и такую величину, как объем, для того, чтобы достичь наиболее рациональной компоновки этих элементов. Вычислить объем куба часто бывает необходимо и тем инженерам, которые занимаются созданием проектов контейнеров, железнодорожных вагонов, а также стеллажных систем, использующихся в складском хозяйстве.
Одним из наиболее ярких примеров кубов является знаменитый «магический куб» – оригинальная головоломка, созданная талантливым венгерским преподавателем архитектуры и скульптором Эрне Рубиком и впоследствии названная в его честь. Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет. С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «1974 года) был продан в количестве около 350 000 000 экземпляров, и на сегодняшний день является одной из признанных в мире головоломок. Изначально каждая из его граней состояла из девяти квадратов, но впоследствии появились и более сложные варианты (например, содержащие по двадцать пять элементов). В различных странах проводятся соревнования по сборке этой головоломки на время, а также чемпионаты Европы и мира, организатором которого является организация «World Cube Association» («Всемирная ассоциация кубика»).
Форму куба имеют не только рукотворные, но и некоторые природные сущности, например, кристаллические решетки такого минерала, как флюорит, а также обычной поваренной соли. Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.
simple-math.ru
