30 Преобразование Лапласа » СтудИзба
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Операционное исчисление представляет собой своеобразный и эффективный метод решения различных математических задач, прежде всего, дифференциальных уравнений. В основе операционного исчисления лежит понятие преобразования Лапласа.
3.1. Преобразование Лапласа
Преобразованием Лапласа . называется преобразование, которое ставит в соответствие функции f(t) действительной переменной t функцию F(p) комплексной переменной p по формуле
(3.1)
Несобственный интеграл в правой части формулы (3 1), зависящий от комплексного параметра p, называется интегралом Лапласа.
Интеграл сходится и действительно определяет собой некоторую функцию F(p), если подынтегральная функция f(t) удовлетворяет следующим условиям:
1) f(t) кусочно — непрерывная функция;
2) f(t) = 0 при t < 0;
3) f(t) по абсолютной величине возрастает не быстрее заранее выбранной показательной функции, то есть можно найти такие постоянные M и , что
.
Число называется показателем роста функции f(t).
Функция f(t) действительного аргумента t, удовлетворяющая перечисленным выше трем условиям, называется оригиналом , а функция F(p) комплексного аргумента p, определяемая согласно ( 3.1), называется изображением по Лапласу функции f(t) или просто изображением .
Символически соответствие между оригиналом и изображением записывается обычно так:
или .
Совокупность всех оригиналов f(t) называется пространством оригиналов, а совокупность всех изображений F(p) – пространством изображений.
Изображения простейших функций
1. Пусть оригинал имеет вид
Эта функция широко применяется в приложениях и называется единичной функцией или функцией Хевисайда.
Изображение этой функции найдем по формуле (3.1):
.
Следовательно,
. (3.2)
2. Изображение показательной функции. Пусть , тогда
Следовательно,
. (3.3)
Нахождение изображений непосредственно по формуле (3.1) обычно затруднительно. Во многих случаях изображения по Лапласу могут быть найдены значительно проще, если воспользоваться свойствами преобразования Лапласа.
Свойства преобразования Лапласа
Для практического применения преобразования Лапласа необходимо знать не только изображения отдельных функций, но и правила отображения выполняемых над ними операций. Эти правила формулируются в виде многочисленных теорем, объединяемых общим названием «свойства преобразования Лапласа». Рассмотрим некоторые основные из них.
1. Теорема линейности . Если , то для любых постоянных и линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, то есть
. (3.4)
Пример. Найти изображения функций cos t и sin t.
Согласно формулам Эйлера
.
Учитывая формулу (3.3) и применяя теорему линейности, получим
(3.5)
Аналогично
(3.6)
2. Теорема подобия. Если f(t) = F(p) , то
(3.7)
то есть умножение аргумента оригинала на некоторое число a приводит к делению аргумента изображения и самого изображения на то же число ( к подобному изменению изображения ).
Пример. Найти изображения функций и . Учитывая изображения (3.5) и (3.6) и применяя теорему подобия, получим
. (3.8)
Аналогично
. (3.9)
3. Теорема смещения изображения. Если f(t) = F(p), то для любого числа a (действительного или комплексного)
(3.10)
то есть умножение оригинала на приводит к смещению аргумента изображения на a.
Пример. Найти изображения функций и .
Учитывая формулы (3.8) и (3.9) и применяя теорему смещения изображения, находим
. (3.11)
Аналогично
. (3.12)
4.Теорема запаздывания. Если f(t) = F(p), то для любого положительного
. (3.13)
то есть «включение» оригинала с запаздыванием на время равносильно
умножению изображения на .
Пример. Найти изображение функции f(at — b), если f(t) =F(p). Применяя теоремы подобия и запаздывания, получим
В частности,
(3.14)
. (3.15)
5. Теорема дифференцирования оригинала. Если f(t) = F(p), то
, (3.16)
то есть дифференцирование оригинала сводится к умножению его изображения на p и вычитанию начального значения функции . В (2.16) — правосторонний предел функции f(t).
(3.17)
…………………………………….
(3.18)
В частности, если все начальные значения функции и ее производных равны нулю, то
(3.19)
Для практических приложений эта теорема является самой важной. Из нее следует, что дифференцирование в пространстве оригиналов заменяется существенно более простой операцией — умножением изображения на степень аргумента. Эта теорема лежит в основе операционного метода решения дифференциальных уравнений.
6.Теорема дифференцирования изображения. Если f(t) = F(p), то
……………………..
.
Учитывая, что и применяя последовательно теорему дифференцирования изображения, найдем изображения степенных функций:
(3.20)
7. Теорема интегрирования оригинала . Если f(t) = F(p), то
. (3.21)
Соответствие между некоторыми основными оригиналами и изображениями указано в таблице 4.
Таблица 4
Таблица соответствия
между основными оригиналами и изображениями
Функция – оригинал (f(t) | Изображение F(p) |
1 | |
cos t | |
sin t | |
Примеры нахождения изображений сложных функций
1. .
Так как
, то применяя теорему дифференцирования,
найдем
Следовательно,
.
2.
Применять теорему дифференцирования пять раз, конечно, неудобно. Представим в виде
Так как
, то по теореме смещения изображения
Теперь по теореме линейности находим
3.
Представим в виде Для функции изображение известно:
По теореме дифференцирования изображения — . Следовательно,
4.
Так как
то
5.
Так как то
Учитывая, что , по теоремам подобия и линейности получим
Замечания.
1. Грубой ошибкой будет представление изображения заданных функций в виде произведения изображений, соответствующих каждому из сомножителей, так как умножению оригиналов в пространстве оригиналов соответствует другая операция в пространстве изображений [4,5].
2. Решение приведенных задач возможно различными способами. В пособии указан лишь один из возможных способов решения.
studizba.com
Преобразование Лапласа и передаточные функции
В теории автоматического управления часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператораp = d /dt,так что, dy / dt = py, а pn = dn/ dtn. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p.
В теории автоматического управления широко применяется операторный метод описания линейных систем автоматического управления, использующий интегральное преобразование Лапласа (L – преобразование), имеющее следующий вид:
Данное преобразование называется прямым односторонним преобразованием Лапласа, преобразует функцию времени х(t) – оригинал, в функцию комплексной переменной
X (р) — изображение. Переменная
р = (a +jb)(1.17.)
где a, b — вещественные (действительные) части числа, j – мнимая единица.
Существует также обратный процесс перехода от изображения к оригиналу, называемый обратным преобразованием Лапласа (L-1 – преобразование), имеющее следующий вид:
Существуют требования, являющиеся достаточными условиями, при которых возможно применение преобразования Лапласа:
— функция оригинала х(t) должна быть непрерывна и однозначна при всех t ≥ 0. Непрерывность может быть нарушена только в отдельных точках, которые являются точками разрыва непрерывности первого рода,
— функция оригинала х(t) = 0 для всех t < 0,
— функция оригинала х(t) должна иметь ограниченный порядок возрастания, т.е должны выполняться следующие условия: должны существовать постоянные a > 0, b > 0,
при которыхх(t) < аеbt, при t > 0.
Для часто применяющихся функций и облегчения применения преобразования Лапласа существуют таблицы, пример приведен на рисунке 23.
| № п/п | Вид функции (оригинал) | Изображение функции по Лапласу |
| 1. | x(t) | X(p) |
| 2. | ||
| 3. | A x(t) | A X(p) |
| 4. | 1(t) | 1/p |
| 5. | d(t)=1’(t) | |
| 6. | di x(t)/dti, i=1…n | pi X(p) |
| 7. | X(p)/p | |
| 8. | x(t-t) | e-pt X(p) |
| 9. | e±at | 1/(p±a) |
| 10. | (1/l) e—atSinlt | 1/[(p+a)2+l2] |
| 11. | (1/a)(1-e—at) | 1/(p+a)p |
Рис.23. Таблица преобразования по Лапласу наиболее часто встречающихся функций
Использование преобразования Лапласа дает возможность перейти от производных и интегралов к более простому алгебраическому выражению — функции комплексного переменного р.Используя преобразование Лапласа для дифференциального уравнения системы (1.14.) при нулевых начальных условиях, мы получим операторное описание системы в виде алгебраического уравнения:
Представив отношение изображения выходного параметра системы ко входному, получим передаточную функцию системы, которая не зависит от характера входного воздействия, а характеризует только собственные свойства системы. Данная функция имеет вид:
и в развернутом виде представляется, как:
Следовательно, передаточной функцией называется отношение величины выходного параметра, к величине входного параметра, преобразованных по Лапласу, при нулевых начальных условиях.
Решение однородного дифференциального уравнения определяется корнями характеристического уравнения. Значение переменной р, при котором передаточная функция W(p )= 0, называется нулем, а значение, при котором W(p ) = ∞ называется полюсом передаточной функции. Из (1.21.) следует, что нулями являются корни полинома B(p), а полюсами – корни полинома А(p).
Из выражения (1.20.) можно получить зависимость изображения по Лапласу выходной величины от изображения входной величины, которая будет иметь вид:
Первоначальное дифференциальное уравнение можно решить, применив к изображению выходной величины обратное преобразование Лапласа (1.18.), определив тем самым переходной процесс:
Применим к решению линейного дифференциального уравнения второго порядка, представленного ниже, преобразование Лапласа:
Для этого зададим начальные условия (значения y(1)(t) и y(t) в начальный момент времени t = 0) и изменение во времени x(t). Примем нулевые начальные условия: y(1)(0) = 0, y(0) = 0 и x(t) = 1 (t). С помощью таблицы (рисунок 23) преобразовав по Лапласу первоначальное дифференциальное уравнение, получаем:
Вынесем за скобки Y(р) и X(р), и получим:
Используя таблицу (рисунок 23), находим X(p) = L [1 (t)] =1/p и подставим данное значение в полученное уравнение, которое примет вид:
Решение уравнения относительно изображения выходной величины будет выглядеть таким образом:
Для того, чтобы найти решение дифференциального уравнения, необходимо произвести операцию обратного преобразования Лапласа с изображением Y (р), поэтому для удобства пользования таблицей преобразования необходимо привести трехчлен, находящийся в знаменателе, к удобному виду. Для этого данный трехчлен необходимо разложить на множители:
в котором p1иp2 — будут являться корнями уравнения
Получаем следующее выражение:
которое можно представить в виде суммы:
где С0,С1, С2 — коэффициенты, которые можно найти, решив тождественное уравнение, полученное путем сравнения числителя выражения (1.28.) и выражения (1.27.), деленного на а2. Далее по таблице преобразования Лапласа (рисунок 23) найдем оригиналы для каждого слагаемого и получим следующее решение:
где С0,С1, С2 – коэффициенты, выступающие в качестве постоянных интегрирования, которые могут быть найдены по формулам начальных условий.
Пример применения преобразования Лапласа
Пусть система описывается следующим уравнением:
а0 y ′′ + a1 y ′ + a2 y = k x (1.35.)
Необходимо найти передаточную функцию W(p)системы при
k = 1, а0 = 1, a1 = 3, a
Решение:
Преобразуем уравнение системы с помощью преобразования Лапласа.
Получим следующее выражение:
(a0 p2 + a1 p + a2 )Y (p) = kX (p) (1.36.)
Подставив имеющиеся числовые значения и преобразовав предыдущее выражение, получим значение передаточной функции, равное:
Задание выполнено.
Похожие статьи:
poznayka.org
Преобразование Лапласа и его некоторые свойства

Пьер-Симон де Лаплас
1749–1828

Жан-Батист Жозеф Фурье
1768–1830

Леонард Эйлер
1707–1783
Содержание
Преобразование Лапласа как разложение сигнала по системе затухающих комплексных экспонент Обратное преобразование Лапласа Некоторые свойства преобразования Лапласа Список литературыПреобразование Лапласа как разложение сигнала по системе затухающих комплексных экспонент
Ранее мы рассмотрели преобразование Фурье сигнала :(1) |
где — спектральная плотность сигнала , и — операторы прямого и обратного преобразования Фурье соответственно.
Условием существования преобразования Фурье является абсолютная интегрируемость [1] исходного сигнала сигнала , т.е. сходимость интеграла:
(2) |
При рассмотрении преобразования Фурье предполагается, что время измеряется от минус бесконечности до плюс бесконечности. Кроме того (2) сужает класс сигналов, для которых существует преобразование Фурье.
С другой стороны, все физические процессы имеют начало, поэтому мы можем считать, что исходный сигнал определён на положительном интервале времени, т.е , при .
Для того, чтобы предотвратить расхождение интеграла (2) умножим входной сигнал на , где — вещественная величина. Рассмотрим преобразование Фурье полученного сигнала:
(3) |
Очевидно, зависит от параметра . Тогда можно трактовать как функцию двух вещественных переменных или как функцию одной комплексной переменной . Обозначив получим:
(4) |
Выражение (4) представляет собой разложение по системе затухающих комплексных экспонент , которое носит название преобразования Лапласа, где — оператор преобразования.
Исходный сигнал называют оригиналом, а — образом, или изображением оригинала.
Обратное преобразование Лапласа
Обратное преобразование Фурье (3) от имеет вид:(5) |
Умножим левую и правую части (5) на , получим:
(6) |
Учтём, что , изменим переменную интегрирования с на :
(7) |
При этом верхний и нижний пределы интегрирования равны:
(8) |
Окончательно (6) с учётом 7 и (8):
(9) |
Выражение (9) определяет обратное преобразование Лапласа, которое обозначается оператором .
Некоторые свойства преобразования Лапласа
Свойство линейностиПусть сигнал . Тогда преобразование Лапласа :
(10) |
Следствием (10) является умножение на константу:
(11) |
Свойство подобия (масштабирование по аргументу)
Пусть сигнал имеет образ . Тогда изображение масштабированного во времени сигнала равно:
(12) |
Аналогично можно показать [2], что масштабирование образа по аргументу приводит к оригиналу вида:
(13) |
Преобразование Лапласа задержанного сигнала
Рассмотрим преобразование Лапласа сигнала , задержанного во времени на положительную величину .
(14) |
Важно отметить, что (14) справедливо, если задержка положительна, как это показано на рисунке 1.
Рисунок 1. Пример положительной и отрицательнойзадержки сигнала
Если же задержка отрицательна, то [2, стр. 40–41]:
(15) |
Аналогичное свойство смещения образа:
(16) |
Таким образом, смещение образа на произвольное комплексное приводит к умножению сигнала на .
Свойство дифференцирования оригинала и образа
Пусть дан сигнал и его преобразование Лапласа равно . Рассмотрим преобразование Лапласа производной сигнала :
(17) |
Применяя правило интегрирования по частям [3, стр. 330]:
(18) |
где — значение сигнала при . Если функция при имеет разрыв, то вместо необходимо брать правый предел :
(19) |
при стремлении к нулю справа.
Таким образом, использование аппарата преобразования Лапласа позволяет заменить дифференцирование умножением образа на переменную . Это важнейшее свойство дало возможность перейти от дифференциальных уравнений при анализе цепей переменного тока к алгебраическим и использовать всю мощь аппарата операционного исчисления и теории функций комплексного переменного для синтеза и анализа электрических цепей.
Приведем также выражение для обратного преобразования Лапласа производной образа [4, стр. 224]. Пусть — образ сигнала . Тогда
(20) |
где — производная -го порядка образа .
Свойство интегрирования оригинала и образа
Пусть сигнал есть результат интегрирования сигнала :
(21) |
Рассмотрим преобразование Лапласа от :
(22) |
Изменим порядок интегрирования и получим:
(23) |
Получили еще одно важнейшее свойство: образ интеграла от входного сигнала равен образу этого сигнала, деленного на переменную . Это свойство также позволяет заменить интегральные уравнения и системы на алгебраические.
Преобразование Лапласа свертки двух сигналов
Пусть сигнал представляет собой свертку двух сигналов и , определяемую соотношением:
(24) |
Важность интеграла свертки (24) в том, что им описывается результат прохождения сигнала через линейный фильтр с импульсной характеристикой .
Обратим внимание, что пределы интегрирования от 0 до обусловлены тем, что и отличны от нуля только для положительных значений переменной .
Рассмотрим преобразование Лапласа сигнала :
(25) |
Поменяем местами операции интегрирования, и учтем свойство временного сдвига (14):
(26) |
Таким образом, интеграл свертки заменяется произведением образов входного сигнала и образа импульсной характеристики фильтра .
Данное свойство также является очень важным, поскольку анализ многокаскадных фильтров заменяется простым произведением образов импульсных характеристик этих фильтров.
Выводы
В данном разделе мы рассмотрели преобразование Лапласа и его некоторые свойства.Аппарат операционного исчисления является основным инструментом анализа электрических цепей переменного тока, ввиду возможности замены операций дифференцирования и интегрирования алгебраическим умножением и делением на переменную .
Подробнее использование преобразования Лапласа для анализа цепей переменного тока будет рассмотрено в следующем разделе.
Список литературы
[1] Будак, Б.М., Фомин, С.В. Кратные интегралы и ряды. Москва, Наука, 1965, 608 c.
[2] Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.
[3] Ильин, В.А., Позняк Э.Г. Основы математического анализа. Москва, Наука, 1965, 572 c.
[4] Свешников, А.Г., Тихонов, А.Н. Теория функций комплексной переменной. Москва, Наука, 1967, 304 с.
ru.dsplib.org
31 Обратное преобразование Лапласа » СтудИзба
Обратное преобразование Лапласа
При практическом применении преобразования Лапласа всегда приходится решать обратную задачу — построение оригинала по его изображению. Общий метод построения оригинала f(t) по заданному изображению F(p) базируется на теореме обращения ( формуле Меллина ):
(3.22)
где интегрирование проводится по любой бесконечной прямой 7 0Re p = 7g 0, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа [7,8]. Непосредственно формулой (3.22) для нахождения оригинала по известному изображению пользуютя редко. При нахождении оригинала по его изображению обычно применяют таблицы соответствия между оригиналами и их изображениями [5] и свойства преобразования Лапласа.
В самом распространенном случае, когда изображение F(p) является дробно — рациональной функцией вида
,
где A(p) и B(p) — многочлены, причем степень многочлена B(p) больше степени многочлена A(p), оригинал может быть найден разложением дроби A(p) /B(p) на простейшие.
Пример. Дано изображение
Найти оригинал f(t) = F(p).
Разложим заданную дробь на простейшие:
Приводя к общему знаменателю, получим
.
При p = 0 1 = -8A,
При p = 2 5 = 16B,
следовательно, A = -1/8, B = 5/16.
Приравнивая далее коэффициенты, например, при и в левой и правой частях равенства, получим
Поэтому
Применяя теорему линейности, окончательно найдем
Пример. Найти оригинал по его изображению
Разложение данной дроби на простейшие имеет вид
После приведения к общему знаменателю получим
При p = 0 1 = -3A, откуда A = — 1/3;
при p = 3 1 = 9C, откуда C = 1/9.
Приравнивая далее коэффициенты при в правой и левой частях равенства, получим уравнение 0 = B + C, из которого следует B = — 1/9.
Итак,
Если знаменатель рациональной дроби B(p) имеет простые не-
нулевые корни , то есть если
то оригинал функции F(p) может быть найден по формуле
(3.23)
Пример. Найти оригинал по его изображению
Здесь,
Корни знаменателя . Следовательно,
Поэтому
Если один из простых корней знаменателя B(p) равен нулю, то есть B(p) можно представить в виде , где , то оригинал находится по формуле
(3.24)
Здесь суммирование распространяется на все ненулевые корни
многочлена
Пример. Найти оригинал по его изображению
.
Здесь
Корни знаменателя . Поэтому
Применяя формулу (3.24), находим
Если знаменатель рациональной дроби представляет собой квадратный трехчлен, корни которого комплексные, удобно представить его в виде суммы квадратов слагаемых и применить теорему смещения изображения.
Пример. Найти оригинал по его изображению
studizba.com
1 Преобразование Лапласа и его свойства
Лекция №12
Тема: Операторный метод анализа переходных
процессов.
Учебные вопросы
1 Преобразование Лапласа и его свойства.
2 Законы Ома и Кирхгофа в операторной форме. Операторная схема замещения.
3 Алгоритм анализа переходных процессов операторным методом.
4 Определение оригинала по его изображению. Теорема разложения.
Литература: [1] с.331- 342.
Рассмотренный ранее классический метод имеет следующие существенные недостатки:
ограниченность применения, он используется в основном в тех случаях, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие на нее после коммутации является гармонической функцией времени либо постоянно; если внешнее воздействие на цепь после коммутации имеет более сложный характер, то определение вынужденной составляющей реакции цепи существенно затрудняется.
громоздкость при анализе переходных процессов цепей более второго порядка, так как нахождение свободной составляющей и постоянных интегрирований требует решение алгебраических уравнений высокого порядка.
Перечисленных недостатков лишен операторный метод анализа переходных процессов, основанный на применении преобразования Лапласа.
Операторный метод не обладает физической наглядностью в силу математической формализации, но значительно упрощает расчеты. Важная особенность операторного метода состоит в его применимости для функций, которые не являются абсолютно интегрируемыми, например, единичный скачок напряжения, гармоническое напряжение, включаемое в некоторый момент времени, и другие формы сигналов, для которых классический и спектральные методы анализа применить не удается.
Сущность операторного метода заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексного переменного . При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор p. Это существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраической. В операторном методе отпадает необходимость определения постоянных интегрирования. Этим обстоятельством объясняется широкое применение этого метода на практике.
Переход из области действительного переменного в область функций комплексного переменного осуществляется с помощью прямого преобразования Лапласа. После этого решаются алгебраические уравнения относительно изображений искомых функций. Полученное решение алгебраических уравнений обратным преобразованием Лапласа переносится в область действительного переменного.
Математическое обоснование операторного метода впервые дано в 1862г. русским математиком М.Е.Ващенко-Захарченко, который показал возможность применения символического (операторного) исчисления к интегрированию дифференциальных уравнений на основе прямого преобразования Лапласа.
В конце XIXв. английские инженеры-электрики О.Хэвисайд и Д.Карсон успешно применили и развили символический метод решения дифференциальных уравнений для расчета переходных процессов в электрических цепях. Однако строгое обоснование операторный метод получил только в XXв. на базе общей теории функциональных преобразований.
Прямое преобразование
Лапласа определяется уравнением 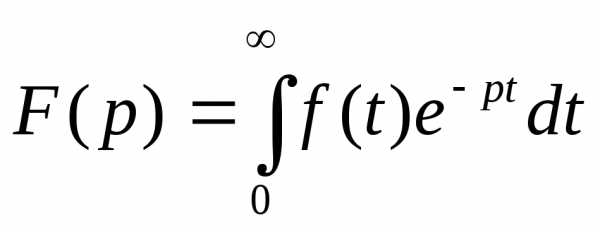
где f(t)
– функция действительного переменного
t,
определенная при 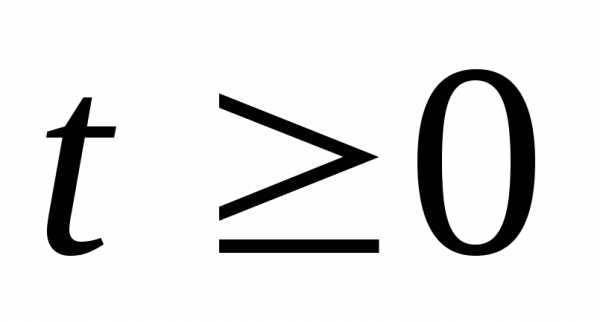 (при t
< 0; f(t)
= 0) и удовлетворяющая условием граниченного
роста:
(при t
< 0; f(t)
= 0) и удовлетворяющая условием граниченного
роста:
где множитель M и показатель роста C0 – положительные действительные числа.
На рис.12.1 изображена область определения комплексного переменного F(p).
Обратное преобразование Лапласа определяют из решения (12.1).
Функция F(p), определяемая уравнением (12.1), называется изображением по Лапласу, а функция f(t) в (12.3) – оригиналом.
Следовательно, оригинал и изображение представляют собой пару функций действительного f(t) и комплексного F(p) переменного, связанных преобразованием Лапласа и поставленных друг другу в строгое соответствие.
Для сокращения записи преобразований (12.1) и (12.3) используют следующую символику:
,
где L – оператор Лапласа.
В дальнейшем для определенности будем использовать знак соответствия.
На основе преобразования Лапласа можно получить изображение любых функций, удовлетворяющих условию (12.2). Имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций.
В таблице 12.1 приведены примеры изображений простых функций.
Таблица 12.1 – Изображения функций по Лапласу
Функция оригинал f(t) | Изображение функции F(p) | |
Выражение функции | Вид функции | |
единичная функция |
| |
|
| |
|
| |
t |
| |
| ||
Рассмотрим некоторые свойства преобразования Лапласа, называемые также теоремами.
Теорема о сложении или линейность преобразования
.
Теорема о дифференцировании
.
Теорема об интегрировании
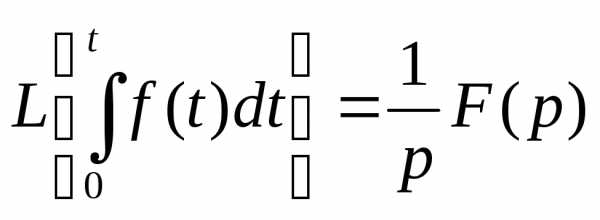 .
.
Теорема запаздывания
.
Преобразование Лапласа позволяет получить соотношения между напряжением и током в операторной форме для резистивного, индуктивного и емкостного элементов.
Изображение напряжения на резистивном элементе
Ur(t) = r i(t) согласно (12.1) примет вид:
Выражение Ur(p) = r I(p) называется законом Ома в операторной форме для резистивного элемента (рис.12.1,а), операторная схема замещения которого представлена на рис.12.1,б.
Рис. 12.1
Изображение
напряжения 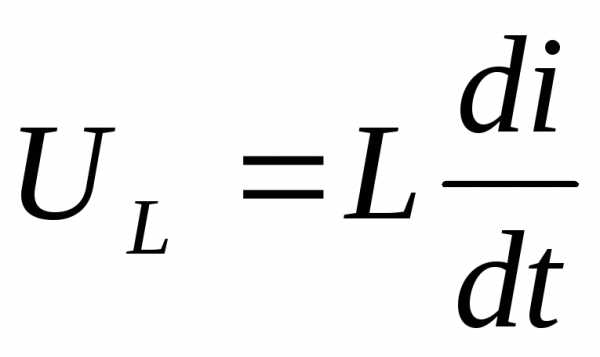 на индуктивном элементе (рис.12.2,а)
согласно (12.4) и (12.5) примет вид:
на индуктивном элементе (рис.12.2,а)
согласно (12.4) и (12.5) примет вид:
UL(p) = — L i(0) + pLI(p), (12.9)
где i(0) = i(0—) = i(0+) – ток в индуктивном элементе в момент коммутации t = 0, учитывающий начальные условия (согласно первого закона коммутации).
Выражению (12.9) соответствует операторная схема замещения индуктивного элемента на рис.12.2,б.
Рис. 12.2
Напряжения на емкостном элементе (рис.12.3,а), начиная с момента времени t = 0 возникновения переходного процесса в общем случае
где Uc(0) = Uc(0—) = Uc(0+) – напряжение на емкостном элементе, соответствующее начальному условию (согласно второго закона коммутации).
Учитывая изображение
единичной функции 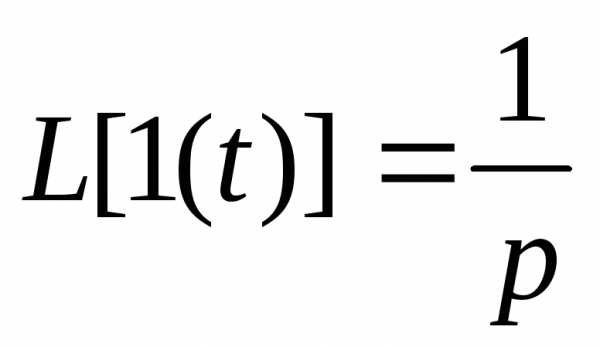 (табл.12.1) и соотношения (12.4) и (12.5), найдем
изображение напряженияUc(t):
(табл.12.1) и соотношения (12.4) и (12.5), найдем
изображение напряженияUc(t):
Выражению (12.10) соответствует схема замещения емкостного элемента в операторной форме на рис.12.3,б.
Рис 12.3
Если начальные условия нулевые, т.е. iL(0—) = 0 и Uc(0—) = 0, то выражения (12.9) и (12.10) примут вид закона Ома в операторной форме для индуктивного элемента
UL(p) = LpI(p) = ZL(p)I(p), (12.11)
где ZL(p) = Lp – операторное сопротивление индуктивного элемента, для емкостного элемента
studfiles.net
Преобразование Лапласа
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра 21
Реферат на тему:
«Преобразование Лапласа»
Выполнила
студентка гр.0850
Киселева Ю.В.
Проверил:
доцент
Данейкин Ю.В.
Томск, 2008г.
Введение
Преобразование Лапласа — интегральное преобразование, связывающее функцию
комплексного переменного (изображение) с функцией действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
1. Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной
, называется функция комплексной переменной , такая что:Правая часть этого выражения называется интегралом Лапласа.
2. Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного
, называется функция действительного переменного, такая что:где
— некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.3. Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции
участвуют значения xДвустороннее преобразование Лапласа определяется следующим образом:
4. Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают
·
-преобразованиеПусть
решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени
, где — целое число, а — период дискретизации. Тогда применяя преобразование Лапласа получим:·
-преобразованиеЕсли применить следующую замену переменных:
получим Z-преобразование:
5. Свойства и теоремы
· Абсолютная сходимость
Если интеграл Лапласа абсолютно сходится при σ = σ0 , то есть существует предел
то он сходится абсолютно и равномерно для
и F(s) — аналитическая функция при ( — действительная часть комплексной переменной s). Точная нижняя грань σa множества чисел σ, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x).· Условия существования прямого преобразования Лапласа
Преобразование Лапласа
существует в смысле абсолютной сходимости в следующих случаях:1. Случай
: преобразование Лапласа существует, если существует интеграл2. Случай σ > σa : преобразование Лапласа существует, если интеграл
существует для каждого конечного
x1 > 0 и
для3. Случай σ > 0 или σ > σa (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции f'(x) (производная к f(x)) для σ > σa .
Примечание: это достаточные условия существования.
· Условия существования обратного преобразования Лапласа
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) — аналитичная функция для
и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём для2. Пусть
,так что
аналитична относительно каждого zk и равна нулю для
, итогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
Примечание: это достаточные условия существования.
· Теорема о свёртке
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
· Умножение изображений
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
· Дифференцирование и интегрирование оригинала
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
В более общем случае (производная n-го порядка):
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
· Дифференцирование и интегрирование изображения. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
mirznanii.com
Применение преобразования Лапласа
Преобразование Фурье
Интеграл Фурье
Преобразование Лапласа
Свойства преобразования Лапласа
Временные характеристики систем управления
В предыдущем разделе использовался оператор дифференцирования
 с помощью которого дифференциальное
уравнение динамики линейной системы
преобразовалось в алгебраическое
уравнение того же порядка. Использование
этого оператора носило чисто символический
характер. Преобразование Лапласа
раскрывает математический и физический
смысл этого оператора и устанавливает
важную связь между передаточной и
весовой функциями линейной системы.
Однако, прежде чем рассматривать
преобразование Лапласа, необходимо
рассмотреть преобразование Фурье,
которое лежит в основе преобразования
Лапласа.
с помощью которого дифференциальное
уравнение динамики линейной системы
преобразовалось в алгебраическое
уравнение того же порядка. Использование
этого оператора носило чисто символический
характер. Преобразование Лапласа
раскрывает математический и физический
смысл этого оператора и устанавливает
важную связь между передаточной и
весовой функциями линейной системы.
Однако, прежде чем рассматривать
преобразование Лапласа, необходимо
рассмотреть преобразование Фурье,
которое лежит в основе преобразования
Лапласа.
Любой сигнал можно представить в виде временной функции (t) и в виде частотной функции F(). Связь между этими двумя формами представления устанавливает преобразование Фурье. Прямое преобразование Фурье позволяет найти F(), если известна (t). Обратное п.Ф. позволяет восстановить (t) по известному спектру F(). Это отображается следующим образом:
прямое п.Ф.
(t)
F()
обратное п.Ф.
В начале рассмотрим п.Ф. периодической функции.
Любую периодическую функцию (t) можно представить в виде синусо-косинусного ряда:
(1)
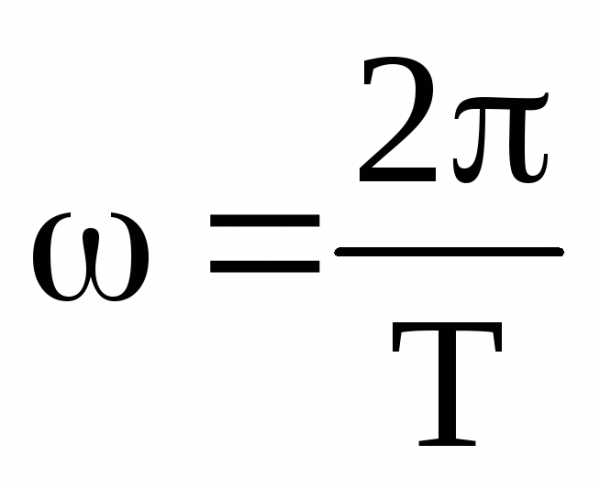 ,
где Т – период функции,
— круговая частота.
,
где Т – период функции,
— круговая частота.
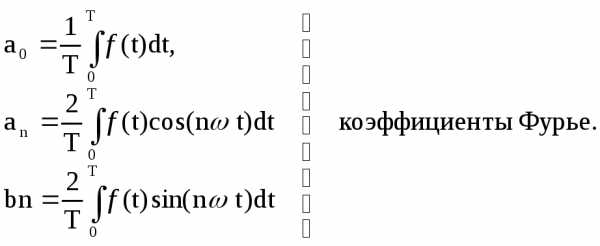
Функцию
(t)
можно представить в виде синусного ряда где
,  ,
An – амплитуда n-ой
гармоники, n – фаза n-ой
гармоники.
,
An – амплитуда n-ой
гармоники, n – фаза n-ой
гармоники.
Если использовать преобразование Эйлера:
, 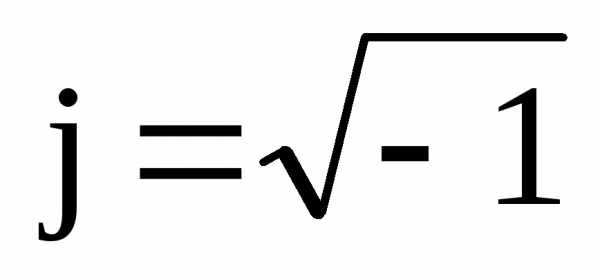 , то выражение (1) можно представить в
экспоненциональной форме:
, то выражение (1) можно представить в
экспоненциональной форме:
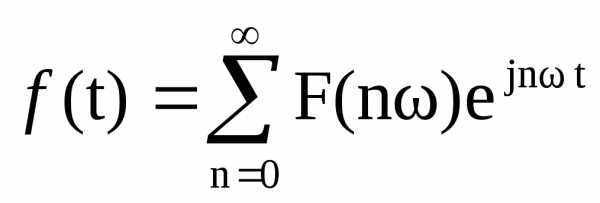 –обратное
преобразование Фурье.
–обратное
преобразование Фурье.
– прямое преобразование Фурье.
Для периодического сигнала частотный спектр является линейчатым. Если функция непериодическая, то тогда преобразования нужно будет вычислять при T. Непериодическую функцию можно считать периодической, если T , 0, тогда
, интеграл Фурье.
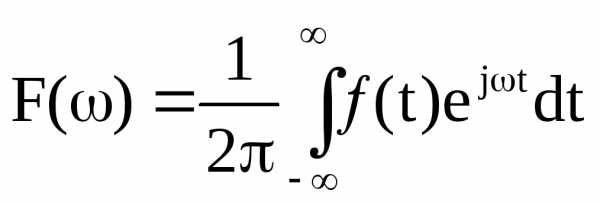 (2)
(2)
Спектр непрерывной функции представляет собой сплошную (непрерывную) функцию. Эти два интеграла существуют, если выполняется условие:
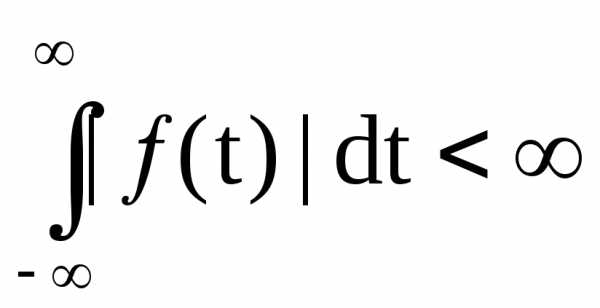 (3)
(3)
Широко используемые в теории управления функции ((t)=1(t), (t)=kt и др.) не удовлетворяют этому условию.
Поскольку для этих функций интегралы Фурье не существуют, поэтому преобразование Фурье применять не имеет смысла. Рассмотрим класс функций (t)=Me—t, где M>0, >0, для которых условие (3) выполняется. Эти функции называются экспоненциальными, они достаточно хорошо отображают большинство процессов, совершающихся в природе. Экспоненциальная функция с параметром <0 отображает затухающий (устойчивый) процесс, причем степень затухания зависит от величины . Функции, для которых =0 являются незатухающими, а для >0 являются неограниченными функциями на полуоси t>0. Обе эти функции соответствуют условно устойчивым (=0) и неустойчивым (>0) процессам, которые на практике встечаются крайне редко. Кроме того, рассматриваются экспоненциальные функции, которые равны нулю для t<0. Такие функции удобно использовать для изучения переходных режимов (момент t=0 соответствует моменту времени, при котором начинается возмущения, порождающие переходной процесс).
Расмотрим
функцию
.
В соответствии с выражением (2) найдем
её спектр для t0: Обозначим через p=+j.
Тогда 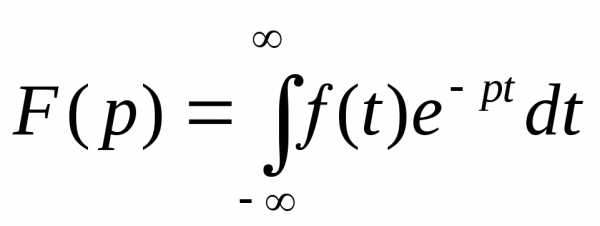 — интеграл Лапласа.
— интеграл Лапласа.
Функцию (t) называют оригиналом, а F(p) – изображением. Показатель p называется комплексной частотой.
Обратное
преобразование Лапласа 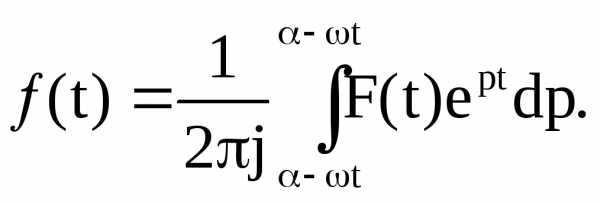
На практике используют преобразование Карсона-Лапласа:
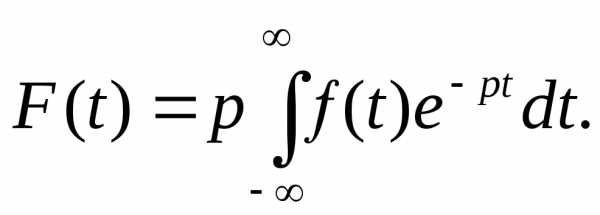 (4)
(4)
Это преобразование позволяет получить в более простой форме изображения некоторых функций. Проведем примеры вычисления преобразования Карсона-Лапласа.
Пример 1.
Пример 2. (t)=e—t. Отметим, что в своей практической работе инженерам нет необходимости вычислять изображения по оригиналу, используя формулу (4). В литературе по теории управления имеются таблицы изображений большинства наиболее употребляемых функций.
Приведем без доказательства некоторые основные свойства преобразования Лапласа.
Пусть тогда
Свойства линейности.
Пусть и
Тогда
Свойство задержки (смещения).
Пусть
Тогда
Свойство дифференцирования.
Пусть
Тогда
где 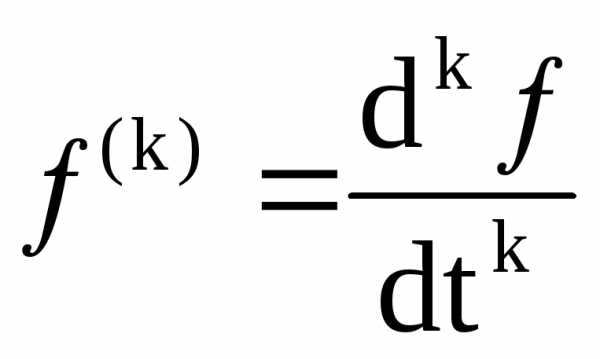
Пример.
Свойство свертки.
Пусть и
Тогда
В пользе приведенных свойств нетрудно убедиться, рассмотрев операторный способ преобразования линей
ного дифференциального уравнения Для упрощения примем Тогда в силу свойств 1,2, и 4
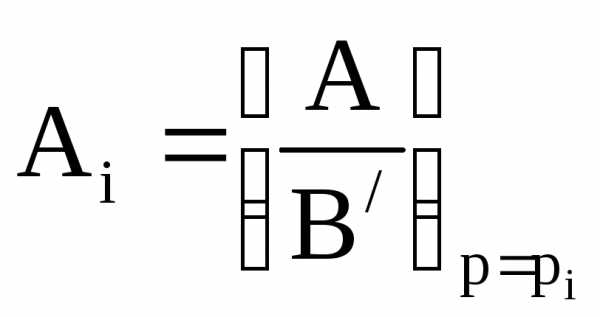
Используя таблицы пребразований Лапласа можно по изображению X(p) получить оригинал X(t), при упомянутых начальных условиях.
В предыдущем разделе было упомянуто о возможностях весовой функции линейной системы.
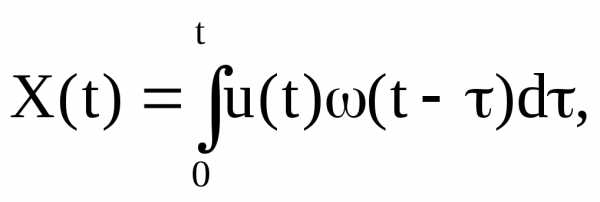 где
u(t), X(t) – значение
входа и выхода линейной системы,
где
u(t), X(t) – значение
входа и выхода линейной системы,
(t) – весовая функция системы.
X(t) – представляет свертку функций u(t) и (t).
Воспользуемся ранее приведенным свойством преобразования Лапласа (свойство свёртки).
Если и , то
Отсюда
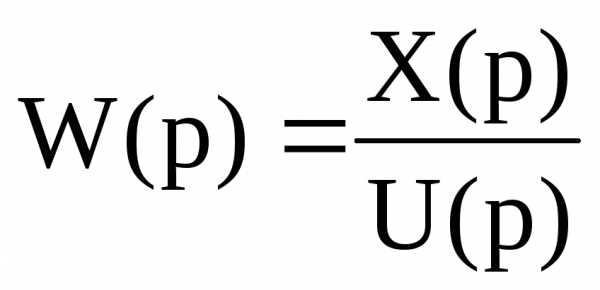 (5).
(5).
Выражение (5) мы назвали передаточной функцией в операторной форме. Теперь можно дать более глубокое толкование выражения (5):
передаточная функция системы W(p) есть отношение изображения выходной величины этой системы к изображению входной величины при условии, что система в начальный момент времени находилась в покое.
Кроме того, можно сделать ещё один очень важный вывод: передаточная функция W(p) есть преобразование Лапласа импульсной (весовой) переходной функции линейной системы.
studfiles.net


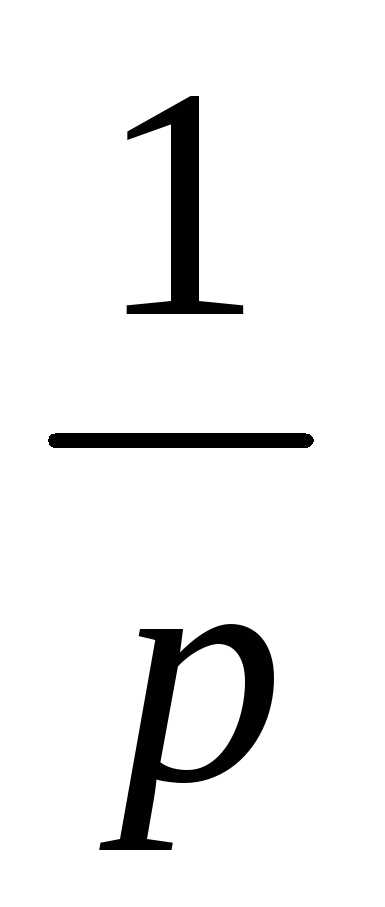
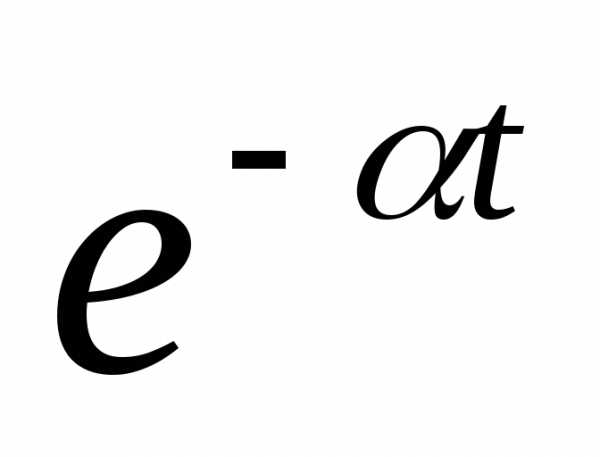
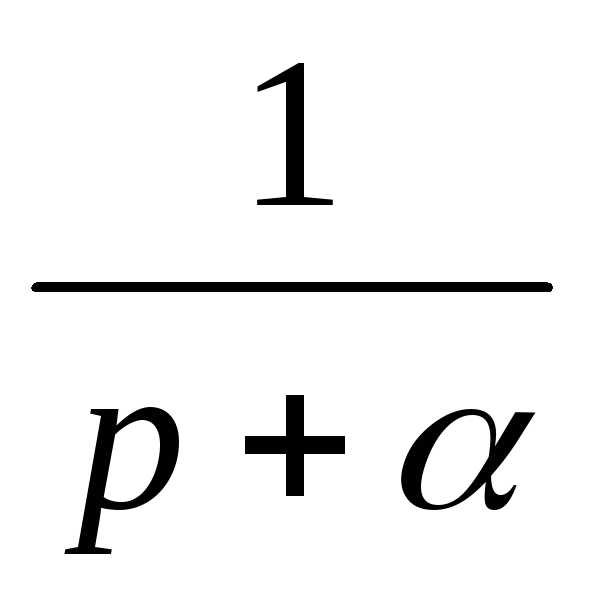
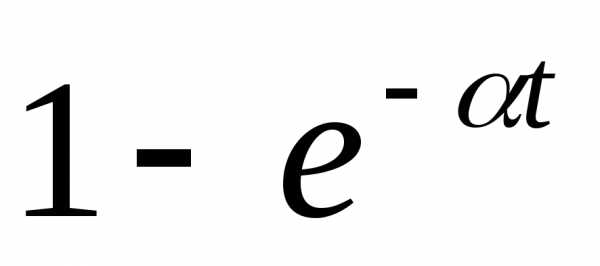
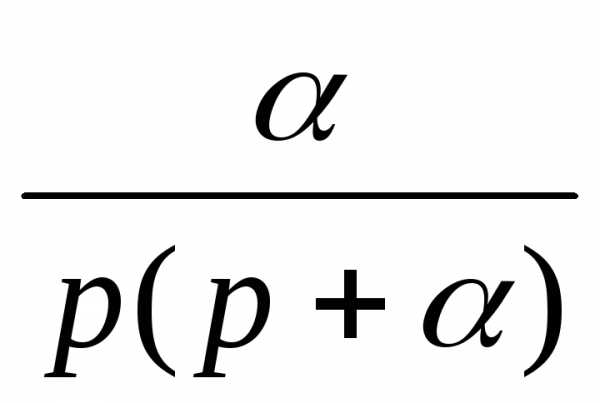
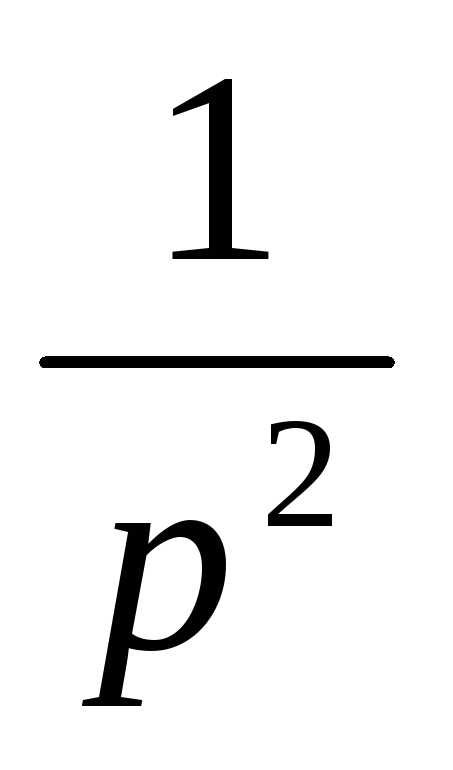
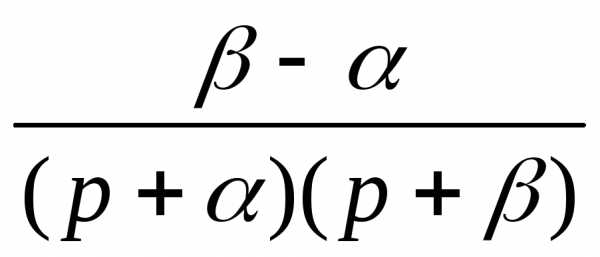
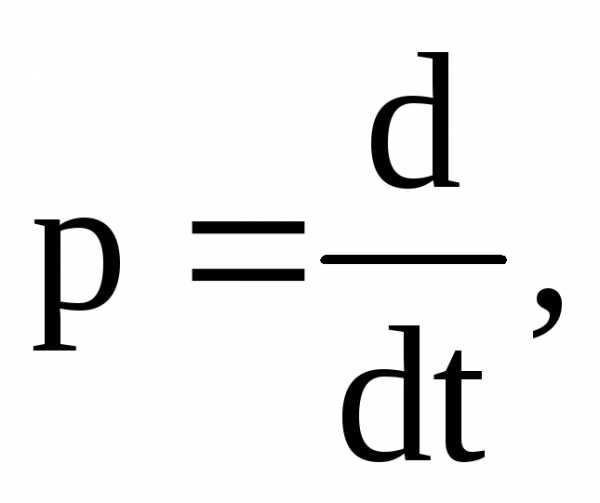 с помощью которого дифференциальное
уравнение динамики линейной системы
преобразовалось в алгебраическое
уравнение того же порядка. Использование
этого оператора носило чисто символический
характер. Преобразование Лапласа
раскрывает математический и физический
смысл этого оператора и устанавливает
важную связь между передаточной и
весовой функциями линейной системы.
Однако, прежде чем рассматривать
преобразование Лапласа, необходимо
рассмотреть преобразование Фурье,
которое лежит в основе преобразования
Лапласа.
с помощью которого дифференциальное
уравнение динамики линейной системы
преобразовалось в алгебраическое
уравнение того же порядка. Использование
этого оператора носило чисто символический
характер. Преобразование Лапласа
раскрывает математический и физический
смысл этого оператора и устанавливает
важную связь между передаточной и
весовой функциями линейной системы.
Однако, прежде чем рассматривать
преобразование Лапласа, необходимо
рассмотреть преобразование Фурье,
которое лежит в основе преобразования
Лапласа.