Как находится обратная матрица: Обратная матрица онлайн

alexxlab / / Разное

Страница не найдена — ПриМат

По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.

Искать:

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2),

Высшая математика.

Лекция 2. Обратная матрица

1. Высшая математика

ЛЕКЦИЯ 2
СЛАУ

2. 3. Обратная матрица

Пусть А – невырожденная (det A≠0)
квадратная матрица (1.2) порядка n.
Е – единичная матрица того же порядка.
Матрица А–1 называется обратной
к матрице А, если выполняются равенства
1
1
A A А А
Е.
Теорема.
( О существовании обратной матрицы).
Матрица А имеет обратную тогда и только тогда,
когда ее определитель отличен от нуля (det A 0,
т.е. когда матрица является невырожденной).
Теорема.
Всякая невырожденная матрица
имеет единственную обратную матрицу:
А11 А21 …. Аn1
1 А12 А22 …. Аn 2
1
A
det A …. …. ….. …..
А
А
…..
А
2n
nn
1n
Aij – алгебраическое дополнение элемента aij.

5. 0.

n =2.
a
11
А a 21
1 А11
A
А12
1
a12 .
a 22
А21 .
А22
0.
Обратная матрица:
1 a 22 a12
A
.
a11
a 21
1

6. Обратная матрица:

n = 3.
a11
A a21
a31
a12
a22
a32
a13
a23 .
a33
Обратная матрица:
A11
1
1
А
A12
det A A
13
A21
A22
A23
A31
A32 .
A33
Пример
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
.
А 1 1 0 . А 1 1 A
A
A
1 0 1
12
22
32
det
A
A13 A23 A33
det A 1.
Решение
Пример
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
.
А 1 1 0 . А 1 1 A
A
A
1 0 1
12
22
32
det
A
A13 A23 A33
det A 1.
1 1 1
A11 ( 1)
Решение
0
01
1,
Найти обратную матрицу к матрице
1 0 0
А 1 1 0 .
1 0 1
Пример
det A 1
1 1 1
A11 ( 1)
Решение
A12 ( 1)1 2
0
0 1
10
1 1
1
1
Найти обратную матрицу к матрице
1 0 0
А 1 1 0 .
1 0 1
Пример
det A 1
1 1 1
A11 ( 1)
Решение
A12 ( 1)1 2
A13 ( 1)1 3
0
01
10
1,
1,
11
1 1
1 0
1,
Пример
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
А 1 1 0 . 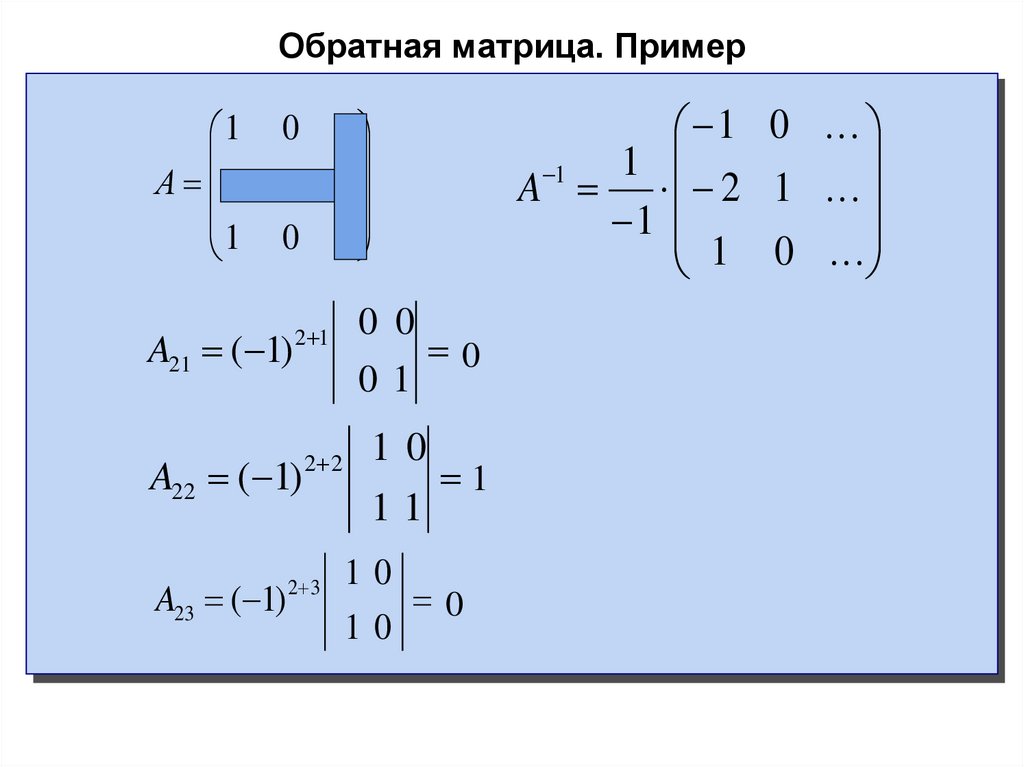А 1 1 A12 A22 A32 .
1 0 1
det A A
13 A23 A33
1
1
1
A
1 .
1
1 1 1 0
1
A11 ( 1)
1,
det A 1.
Решение
A12 ( 1)1 2
A13 ( 1)1 3
0 1
1 0
1 1
1 1
1 0
1,
1,
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
Пример А 1 1 0 . А 1 1 A
.
A
A
12
22
32
1 0 1
det A A
13 A23 A33
Решение
A21 ( 1)
2 1
A22 ( 1)
2 2
A23 ( 1)
2 3
0 0
0,
01
10
1,
11
10
0,
10
1
1
1
A
1
1
1
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
Пример А 1 1 0 . А 1 1 A
.
A
A
12
22
32
1 0 1
det A A
13 A23 A33
A21 ( 1)2 1
Решение
A22 ( 1)
2 2
A23 ( 1)
2 3
11
0 0
0, A 11 11 11
01
1
1
11
10
1,
11
10
0,
10
0
1 .
0
Пример
Решение
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
А 1 1 0 . А 1 1 A12 A22 A32 .
1 0 1
det A A
13 A23 A33
A21 ( 1)
2 1
A22 ( 1)
2 2
A23 ( 1)
2 3
0 0
0,
01
10
1,
11
10
0,
10
1 0
1
1
A 1 1 .
1
1
0
Пример
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
А 1 1 0 А 1 1 A12 A22 A32
1 0 1
det A A
13 A23 A33
0
1 0
A31 ( 1)
0 11 11
1 0
AA 1 1
0
11
1
0
3 2
0
1
1
A32 ( 1)
0
Решение
10
3 1
A33 ( 1)
3 3
0 0
1 0
1
1 1
Пример
Решение
Найти обратную матрицу к матрице
A11 A21 A31
1 0 0
А 1 1 0 А 1 1 A12 A22 A32
1 0 1
det A A
13 A23 A33
1 0 0 1 0 0
1
1
A
1 1 0 1 1 0 .
1
1 0 1
1
0
1
1 0 0
1
0
0
1
0
0
1 1 1 0 1 1 0 0 1 0 .
AA
1 0 1 1 0 1 0 0 1

18. 4. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

(СЛАУ)
К решению систем линейных алгебраических
уравнений
сводятся
многочисленные
практические задачи (по некоторым оценкам
более 75% всех задач).
• Системой линейных алгебраических уравнений,
содержащей т уравнений и n неизвестных, называется
система вида
a11 x1 + a12 x2 + a13 x3 + … +  a1n xn  = b1,
a x + a x + a x + … + a x  = b ,
21 1 22 2
23 3
2n n
2
(2.1)
am1x1 + am 2 x2 + am3 x3 + … + amn xn  = bm , 
где x1, x2,  , xn – неизвестные,
aij– числа (i = 1,  , m; j =1,  , n), называемые
коэффициентами системы,
b1, b2,  , bm – числа, называемые свободными
членами.
• Решением системы (2.1) будем называть
упорядоченный набор чисел x1, x2,  , xn ,
обращающий каждое ее уравнение в верное
равенство.
• Такую систему удобно записывать в компактной
матричной форме:
А  Х=В.
(2.2)
a11 a12
a
a22
21
А a31 a32
am1 am 2
a13 … a1n
a23 … a2 n – матрица коэффициентов системы.
a33 … a3n
b1
b
am3 … amn
2 — (столбец правых частей)
В b3
вектор-столбец из
свободных членов bi.
bm
x1
x2
Х x3
— вектор-столбец из неизвестных x .
j 
x
n
a11 a12
a
a22
21
A a31 a32
am1 am 2
a13 … a1n b1
a23 … a2 n b2
(2.3)
a33 … a3n b3 .
am3 … amn bm
• Решить систему — значит найти все ее решения или
доказать, что решений нет.
Система линейных уравнений
хотя бы одно решение
совместная
единственное
решение
определенная
нет решения
несовместная
более одного решения
неопределенная
• В случае неопределенной СЛАУ каждое ее
решение называется частным решением.
• Совокупность всех частных решений называется
общим решением.
• Система, у которой все свободные члены равны нулю
(b1 = b2 = = bn = 0), называется однородной.
a11 x1 + a12 x2 + a13 x3 + … +  a1n xn  = 0,
a x + a x + a x + … + a x  = 0,
21 1 22 2
23 3
2n n
(2.4)
am1x1 + am 2 x2 + am3 x3 + … + amn xn  = 0. 
• Однородная система всегда совместна,
совместна так как набор
из n нулей (тривиальное решение) удовлетворяет
любому уравнению из (2. 4).
• Если число уравнений системы совпадает с
числом неизвестных (m=n), то система
называется квадратной.
• Если определитель матрицы A квадратной
системы Δ =det A≠ 0,
0 то система имеет
единственное решение.
решение
• Если det A= 0,
0 то система либо имеет
бесконечное множество решений,
решений либо
несовместна.

28. 4.1. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ РЕШЕНИЯ СЛАУ

29. Применение обратной матрицы для решения СЛАУ

В матричной форме записи квадратная определенная система
уравнений имеет вид:
АХ=В.
(2.2*)
Так как det А= 0, существует обратная матрица А–1.
Если умножить обе части (2.2*) на А–1 слева, то получим формулу
для нахождения столбца неизвестных Х:
1
1
A A X A B
Е
Х
1
X A B.
(2. 5)
Пример. Решить матричным способом систему
уравнений
3 x 2 y 7,
x y 4.
Решение.
А 13 21 .
A
1
1 a 22
a 21
7
В .
4
a12
.
a11
3 2
1 1
5.
1 1 2
А
1 3 .
5
1
х
1 1 2 7 1 15 3
1
.
Х А В
1 3
4 5 5 1
5
у

32. швейцарский математик, один из создателей линейной алгебры

(1704 -1752)
швейцарский математик, один из
создателей линейной алгебры
X A 1 B.
(2. 5)
Пусть квадратная определенная система в матричной
форме имеет вид :
АХ=В, det А= 0.
(2.6)
Тогда из (2.5) получим, что решение (2.6) находится по
формулам:
x1
A11
x
A
1
2 12
M K
xn
A1n
A21 K
A22 K
K
K
A2 n K
An1 b1
A11b1 A21b2 L An1bn
A b A b L A b
An 2
b
1
22 2
n2 n
2 12 1
K M
M
Ann bn
A1nb1 A2 nb2 L Annbn
где
i
Формулы (2.7) отыскания
решения системы (2.6)
,
называются формулами
Крамера.
Крамера
1
2
n
. (2.7)
x1 , x2 ,K , xn
определитель матрицы, полученной из А заменой ее
j-го столбца на столбец правых частей системы, j=1, 2,. .n.
Частный случай n=2.
(2.8)
Введем в рассмотрение следующие три определителя для
матрицы системы (2.8):
Теорема (правило Крамера).
Если 0, то система (2.8) имеет единственное
решение, которое находится по формулам
х
х
; у
у
.
(2.9)
Пример. Решить по правилу Крамера систему уравнений
:
3 x 2 y 7,
x y 4.
Решение. Вычислим определитель системы
x
7 2
4 1
15,
y
3 2
1 1
3 7
1 4
5 0.
5.
Cогласно (2.9), получаем
x 15
x
3,
5
y
5
y
1.
5
3x 2 y 7
x y 4
n=3.
Рассмотрим систему трех линейных уравнений с
тремя неизвестными
а11 х1 а12 х2 а13 х3 b1,
а21х1 а22 х2 а23 х3 b2 ,
а31х1 а32 х2 а33 х3 b3.
(2.10)
Обозначим
а11 а12 а13
b1 а12 а13
а21 а22 а23 , 1 b2 а22 а23 , 2
а31 а32 а33
b3 а32 а33
а11 b1 а13
а21 b2 а23 , 3
а31 b3 а33
а11 а12 b1
а21 а22 b2 .
а31 а32 b3
Вспомогательные определители 1, 2, 3 получаются
из определителя матрицы системы (2. 10) заменой
соответствующего столбца столбцом свободных
членов.
n = 3.
Теорема (правило Крамера). Если 0, то система
(2.10) имеет единственное решение, которое
находится по формулам Крамера
х1
1
, х2
2
, х3
3
.
(2.11)

39. Окончание лекции

2.4: Обратные матрицы — Математика LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    37849
    • Рупиндер Секон и Роберта Блум
    • Колледж Де Анза

    Цели обучения

    В этом разделе вы научитесь:

    1. Находить обратную матрицу, если она существует.
    2. Используйте инверсию для решения линейных систем. {-1}\).

      Пример \(\PageIndex{1}\)

      Имея приведенные ниже матрицы \(A\) и \(B\), убедитесь, что они обратные.

      \[A=\left[\begin{array}{ll}
      4 & 1 \\
      3 & 1
      \end{array}\right] \quad B=\left[\begin{array}{cc }
      1 & -1 \\
      -3 & 4
      \end{array}\right] \nonumber \]

      Решение

      Матрицы являются обратными, если произведение \(AB\) и \(BA\ ) оба равны единичной матрице размерности \(2 \times 2\): \(I_2\),

      \[\mathrm{AB}=\left[\begin{array}{ll}
      4 & 1 \\
      3 & 1
      \end{array}\right]\left[\begin{array}{cc }
      1 & -1 \\
      -3 & 4
      \end{array}\right]=\left[\begin{array}{ll}

      1 & 0 \\
      0 & 1
      \end{array} \right]=\mathrm{I}_{2} \nonumber \]

      и

      \[\mathrm{BA}=\left[\begin{array}{cc}
      1 & -1 \\
      — 3 & 4
      \end{массив}\right]\left[\begin{array}{ll}
      4 & 1 \\
      3 & 1
      \end{массив}\right]=\left[\begin{массив {ll}
      1 & 0 \\
      0 & 1
      \end{массив}\right]=\mathrm{I}_{2} \nonumber \]

      Очевидно, что это так; следовательно, матрицы A и B обратны друг другу.

      Пример \(\PageIndex{2}\)

      Найдите обратную матрицу \(\mathrm{A}=\left[\begin{array}{ll}
      3 & 1 \\
      5 & 2
      \ конец{массив}\справа]\).

      Решение

      Предположим, \(A\) имеет обратное значение, и оно равно

      \[B=\left[\begin{array}{ll}
      a & b \\
      c & d
      \end{массив}\right] \nonumber \]

      Затем \(AB = I_2\): \(\left[\begin{array}{cc}
      3 & 1 \\
      5 & 2

      \end{массив}\right]\left[\begin{array}{ll}
      a & b \\
      c & d
      \end{массив}\right]=\left[ \begin{array}{ll}
      1 & 0 \\
      0 & 1
      \end{array}\right]=I_{2}\)

      После умножения двух матриц в левой части мы получаем

      \[\left[\begin{array}{cc}
      3 a+c и 3 b+d \\
      5 a+2 c и 5 b+2 d
      \end{массив}\right]=\left[\begin{массив}{cc}
      1 & 0 \\
      0 & 1
      \end{массив}\ right] \nonumber \]

      Приравнивая соответствующие записи, получаем четыре уравнения с четырьмя неизвестными:

      \[\begin{array}{ll}
      3 a+c=1 & 3 b+d=0 \\
      5 a+2 c=0 & 5 b+2 d=1
      \end{array} \nonumber \]

      Решая эту систему, получаем: \(a = 2 \quad b = -1 \quad c = — 5 \quad d = 3\)
      Следовательно, обратной матрицей \(A\) является \(B=\left[\begin{array}{cc}
      2 & -1 \\
      -5 & 3
      \end{массив}\right] \nonnumber\)

      В этой задаче нахождение обратной матрицы \(A\) сводилось к решению системы уравнений:

      \[\begin{array}{ll}
      3 a+c=1 и 3 b+d=0 \\
      5 a+2 c=0 и 5 b+2 d=1
      \end{array} \ не число \]

      На самом деле это можно записать как две системы, одну с переменными \(a\) и \(c\), а другую с \(b\) и \(d\). Расширенные матрицы для обоих приведены ниже.

      \[\left[\begin{array}{llll}
      3 & 1 & | & 1 \
      5 & 2 & | & 0
      \end{массив}\right] \text { и }\left[\begin{массив}{llll}
      3 & 1 & | & 0 \
      5 & 2 & | & 1
      \end{массив}\right] \nonumber \]

      Глядя на две расширенные матрицы, мы замечаем, что матрица коэффициентов для обеих матриц одинакова. Это означает, что операции над строками метода Гаусса-Жордана также будут такими же. Можно сэкономить много работы, если два правых столбца сгруппировать вместе, чтобы сформировать одну расширенную матрицу, как показано ниже. 9{-1}\) матрица.

      То, что вы только что увидели, не случайно. Это метод, который часто используется для нахождения обратной матрицы. Перечислим шаги следующим образом:

      Метод нахождения обратной матрицы

      1. Запишите расширенную матрицу \([ A | I_n ]\).

      2. Запишите расширенную матрицу из шага 1 в сокращенной ступенчатой ​​форме строк.

      3. Если редуцированная ступенчатая форма строки в 2 есть \([ I_n | B]\), то \(B\) является обратной формой \(A\).

      4. Если левая часть редуцированного эшелона строки не является единичной матрицей, то обратной не существует.

      Пример \(\PageIndex{3}\)

      Имея приведенную ниже матрицу A, найдите ее обратную.

      \[A=\left[\begin{array}{ccc}
      1 & -1 & 1 \\
      2 & 3 & 0 \\
      0 & -2 & 1
      \end{массив}\right] \номер \]

      Решение

      Расширенную матрицу запишем следующим образом.

      \[\left[\begin{массив}{ccccccc}

      1 & -1 & 1 & | & 1 & 0 & 0 \\
      2 & 3 & 0 & | & 0 & 1 & 0 \\
      0 & -2 & 1 & | & 0 & 0 & 1
      \end{array}\right] \nonumber \]

      Мы уменьшим эту матрицу, используя метод Гаусса-Жордана.

      Умножив первую строку на -2 и прибавив ее ко второй строке, мы получим

      \[\left[\begin{array}{ccccccc}
      1 & -1 & 1 & | & 1 & 0 & 0 \\
      0 & 5 & -2 & | &-2&1&0\
      0 & -2 & 1 & | & 0 & 0 & 1
      \end{array}\right] \nonumber \]

      Если поменять местами вторую и третью строки, то получится

      \[\left[\begin{array}{ccccccc}
      1 & -1 и 1 и | & 1 & 0 & 0 \\
      0 & -2 & 1 & | & 0 & 0 & 1 \\
      0 & 5 & -2 & | & -2 & 1 & 0
      \end{массив}\right] \nonumber \]

      Разделить вторую строку на -2. Результат

      \[\left[\begin{array}{ccccccc}
      1 & -1 & 1 & | & 1 & 0 & 0 \\
      0 & 1 & -1 / 2 & | & 0 & 0 & -1 / 2 \

      0 & 5 & -2 & | & -2 & 1 & 0
      \end{array}\right] \nonumber \]

      Давайте проделаем здесь две операции. 1) Прибавьте вторую строку к первой, 2) Прибавьте -5 раз вторую строку к третьей. И мы получаем

      \[\left[\begin{array}{ccccccc}
      1 & 0 & 1 / 2 & | & 1 & 0 & -1 / 2 \\
      0 & 1 & -1 / 2 & | &0&0&-1/2\
      0 и 0 и 1 / 2 и | & -2 & 1 & 5 / 2
      \end{array}\right] \nonumber \]

      Умножение третьей строки на 2 дает

      \[\left[\begin{array}{ccccccc}
      1 & 0 и 1 / 2 и | & 1 & 0 & -1 / 2 \\
      0 & 1 & -1 / 2 & | & 0 & 0 & -1 / 2 \\
      0 & 0 & 1 & | & -4 & 2 & 5
      \end{массив}\right] \nonumber \]

      Умножьте третью строку на 1/2 и прибавьте ко второй. 9{-1}=\left[\begin{array}{rrr}
      3 & -1 & -3 \\
      -2 & 1 & 2 \\
      -4 & 2 & 5
      \end{массив}\right ]\)

      Нужно проверить результат, перемножив две матрицы, чтобы увидеть, действительно ли произведение равно единичной матрице.

      Теперь, когда мы знаем, как найти обратную матрицу, мы будем использовать обратную сторону для решения систем уравнений. Этот метод аналогичен решению простого уравнения, подобного приведенному ниже. \[ \frac{2}{3}x = 4 \nonumber \]

      Пример \(\PageIndex{4}\)

      Решите следующее уравнение: \(\frac{2}{3}x = 4\)

      Решение

      Чтобы решить приведенное выше уравнение, мы умножаем обе части уравнения мультипликативным обратным к \(\frac{2}{3}\), которое оказывается равным \(\frac{3}{2}\). Получаем

      \[\begin{array}{l}
      \frac{3}{2} \cdot \frac{2}{3} x=4 \cdot \frac{3}{2} \\
      x =6
      \конец{массив} \номер\]

      Мы используем пример \(\PageIndex{4}\) в качестве аналогии, чтобы показать, как решаются линейные системы вида \(AX = B\).

      Чтобы решить линейную систему, сначала запишем систему в матричном уравнении \(AX = B\), где \(A\) — матрица коэффициентов, \(X\) — матрица переменных, а \(B\ ) матрица постоянных членов.
      Затем мы умножаем обе части этого уравнения на мультипликативную обратную матрицу \(A\).

      Рассмотрим следующий пример.

      Пример \(\PageIndex{5}\)

      Решите следующую систему

      \begin{aligned}
      3 x+y&=3 \\
      5 x+2 y&=4
      \end{align}

      Решение

      Чтобы решить приведенное выше уравнение, сначала мы представим систему как

      \[AX = B \nonumber \]

      , где A — матрица коэффициентов, а B — матрица постоянных терминов. Получаем

      \[\left[\begin{array}{ll}
      3 & 1 \\
      5 & 2
      \end{array}\right]\left[\begin{array}{l}
      x \ \
      y
      \end{массив}\right]=\left[\begin{array}{l}
      3 \\
      4
      \end{массив}\right] \nonumber \] 9{-1}\), получаем

      \[\begin{array}{c}
      {\left[\begin{array}{cc}
      2 & -1 \\
      -5 & 3
      \end{ array}\right]\left[\begin{array}{cc}
      3 & 1 \\
      5 & 2
      \end{array}\right]\left[\begin{array}{c}
      x \\
      y
      \end{массив}\right]=\left[\begin{array}{cc}
      2 & -1 \\
      -5 & 3
      \end{массив}\right]\left[\begin{ array}{c}
      3 \\
      4
      \end{массив}\right]} \\
      {\left[\begin{массив}{cc}
      1 & 0 \\
      0 & 1
      \end{массив}\right]\left[\begin{array}{c}
      x \\
      y
      \end{массив}\right]=\left[\begin{array}{c}
      2 \ \
      -3
      \end{массив}\right]} \\
      {\left[\begin{array}{c}
      x \\
      y
      \end{массив}\right]=\left[\begin {array}{c}
      2 \\
      -3
      \end{array}\right]}
      \end{array} \nonumber \]

      Следовательно, \(x = 2\) и \(y = -3\).

      Пример \(\PageIndex{6}\)

      Решите следующую систему:

      \begin{aligned}
      x-y+z &=6 \\
      2 x+3 y &=1 \\
      -2 y+z &=5
      \end{aligned}

      Решение

      Чтобы решить приведенное выше уравнение, запишем систему в матричной форме \(AX = B\) следующим образом:

      \[\left[\begin{array}{rrr}
      1 & -1 & 1 \\
      2 & 3 & 0 \\
      0 & -2 & 1
      \end{array }\right]\left[\begin{array}{l}
      x \\
      y \\
      z
      \end{массив}\right]-\left[\begin{array}{l}
      6 \\
      1 \\
      5
      \end{массив}\right] \nonnumber \] 9{-1}\), получаем

      \[\left[\begin{array}{rrr}
      3 & -1 & -3 \\
      -2 & 1 & 2 \\
      -4 & 2 & 5
      \end{массив}\right]\left[\begin{array}{rrr}
      1 & 1 & 1 \\
      2 & 3 & 0 \\
      0 & 2 & 1
      \end{массив}\right ]\left[\begin{array}{l}
      x \\
      y \\
      z
      \end{array}\right]=\left[\begin{array}{rrr}
      3 & -1 & — 3 \\
      -2 & 1 & 2 \\
      -4 & 2 & 5
      \end{массив}\right]\left[\begin{массив}{l}
      6 \\
      1 \\
      5
      \end{array}\right] \nonumber \]

      После перемножения матриц получаем

      \begin{aligned}
      {\left[\begin{array}{ lll}
      1 & 0 & 0 \\
      0 & 1 & 0 \\
      0 & 0 & 1
      \end{array}\right]\left[\begin{array}{l}
      x \\
      y \\
      z
      \end{массив}\right]=\left[\begin{array}{r}
      2 \\
      -1 \\
      3
      \end{массив}\right]} \\
      { \left[\begin{array}{l}
      х \\
      у \\
      z
      \end{массив}\right]=\left[\begin{array}{r}
      2 \\
      -1 \\
      3
      \end{массив}\right]}
      \end{выровненный}

      Напоминаем читателю, что не всякая система уравнений может быть решена методом обращения матриц. Хотя метод Гаусса-Жордана работает для любой ситуации, метод обратной матрицы работает только в тех случаях, когда существует обратная квадратная матрица. В таких случаях система имеет единственное решение.

      Метод нахождения обратной матрицы

      1. Запишите расширенную матрицу \(\left[\mathrm{A} | \mathrm{I}_{\mathrm{n}}\right]\).
      2. Запишите расширенную матрицу на шаге 1 в сокращенной ступенчатой ​​форме строк.
      3. Если редуцированная форма эшелона строк в 2 имеет вид \(\left[\mathrm{I}_{\mathrm{n}} | \mathrm{B}\right]\), то \(B\) является обратным \(А\).
      4. Если левая часть редуцированного эшелона строки не является единичной матрицей, то обратная матрица не существует.

      Метод решения системы уравнений при наличии единственного решения 9{-1}B \text{ где } I \text{ — единичная матрица} \nonumber \]

      Эта страница под названием 2.4: Inverse Matrices распространяется под лицензией CC BY 4. 0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

      1. Наверх
        • Была ли эта статья полезной?
        1. Тип изделия
          Раздел или Страница
          Автор
          Рупиндер Сехон и Роберта Блум
          Лицензия
          СС BY
          Версия лицензии
          4,0
          Показать страницу TOC
          нет
        2. Теги
          1. обратная матрица
          2. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html

        Обратная матрица nxn

        Обратная матрица nxn

        ОБРАТНАЯ МАТРИЦА n x n

        См. наш текст (Рольф, стр. 163) для обсуждения обратных матриц. Коротко о матрице инверсии ведут себя как обратные для действительных чисел : произведение матрицы и его обратная матрица является единичной.

        Пусть A будет именем нашей матрицы nxn : неквадратные матрицы не имеют обратной. Следующие шаги дадут инверсию A, записанную A -1 . Обратите внимание на сходство между этим методом и методом GAUSS/JORDAN, используемым для решения системы уравнения.

        [1]
        Увеличьте nxn-матрицу A с помощью nxn единичная матрица я н ; см. текст ( Rolf, стр. 163) или прокрутите ниже
        [ А | I п ]
        [2]
        Поворот на матрице элементы в позициях 1-1, 2-2, 3-3, продолжая через n-n в таком порядке, с целью создания копии единичной матрицы я н слева часть расширенной матрицы.
        Если один из поворотных элементов равен нулю, то сначала поменять местами это ряд с нижним рядом. Если такой обмен не производит ненулевой опорный элемент, то матрица A не имеет обратной. Этот шаг [2] эквивалентен шагу 2 на стр. 163 нашего текста Рольф, что приводит к (УМЕНЬШЕННОЙ) ДИАГОНАЛЬНОЙ ФОРМЕ. Посмотрите пример ниже и попробуйте Pivot Engine, когда вы проверяете свой поворотные навыки.
        [ А | я п ] ===> [ I n | А -1 ]
        [3]
        Когда шаг [2] выше выполнен, правая половина последней расширенная матрица будет искомой обратной, А -1 ; пиши отдельно, и готово, как в примере ниже.
        Примечание 1 : Профессор М c Фарландские имена строковые операции совсем немного в отличие от нашего текста : следуйте стилю именования профессора МакФарланда.

        Примечание 2 : Проверьте Prof M c Farland’s интерактивныйПОВОРОТНЫЙ ДВИГАТЕЛЬ при использовании операций со строками.

        Примечание 3 : Сравните 3 вышеуказанных шага для те, которые используются в GAUSS/JORDAN.

        ПРИМЕР ПОИСКА ОБРАТНОЙ МАТРИЦЫ A

        См. наш текст (Рольф, стр. 163) в качестве примера; ниже другой пример :

        Мы должны найти обратную матрицу A справа  
        А = 1
         2
        -2        		 -1
         1
        -2        		 3
        2
        1
         
        Ниже представлена ​​та же матрица A, дополненная айдентика 3×3 матрица. Первый стержень, обведенный красным
        		 Ниже приведены операции со строками, необходимые для первого поворотный
        Следующий поворот на «3» в позиции 2-2 ниже, обведенной красным
        Столбцы единичной матрицы 3×3 окрашены в синий цвет. как они снова появляются на левой стороне
        Ниже результат выполнения P1, так что стержень (позиция 2-2) теперь «1». Далее выполняем Р2
        		 Рядные операции
        из P2
        ниже
        Результат второго поворота ниже. Мы сейчас развернуться на элемент в позиции 3-3, обведен красным ниже
        Ниже приведен результат выполнения P1, поэтому точка поворота (позиция 3-3) теперь «1». Далее выполняем П2.
        		 Ниже приведены операции строки P2
        Результат третьего (и последнего) поворота ниже с Идентификационная матрица 3×3 синего цвета
        Матрица ниже НЕ является A -1
          (УМЕНЬШЕННЫЙ)
        ДИАГОНАЛЬ
        ФОРМА
        E
        Таким образом, наш последний шаг —
        отделить нужное обратное
        из приведенной выше матрицы :         		 
        А -1 =

        Примечание : МАТРИЧНЫЙ ОБРАТНЫЙ МЕТОД для решения системы уравнений будет использовать вышеупомянутое обсуждение, и даже продолжить вышеупомянутую проблему.

        No related posts.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *