Таблица градусов cos 120 градусов – Косинус 120 градусов

Таблица косинусов

Таблица косинусов — это удобное решение для проведения быстрых расчетов, когда нужно получить числовое значение косинуса того или иного угла. В статье мы узнаем, что такое косинус, чем похожи и как связаны таблица синусов и косинусов, как использовать таблицу синусов Брадиса для получения конкретных числовых значений косинуса того или иного угла.

Что такое косинус угла и как его применять в решении задач

Начнем с того, что каждый знает, что такое прямоугольный треугольник. Им называется такой треугольник, у которого один из углов (C) прямой (равен 90°), остальные два угла (𝛼 и 𝛽) острые. Он имеет стандартное обозначение углов и сторон. Тогда, что такое косинус угла, можно рассмотреть дальше.

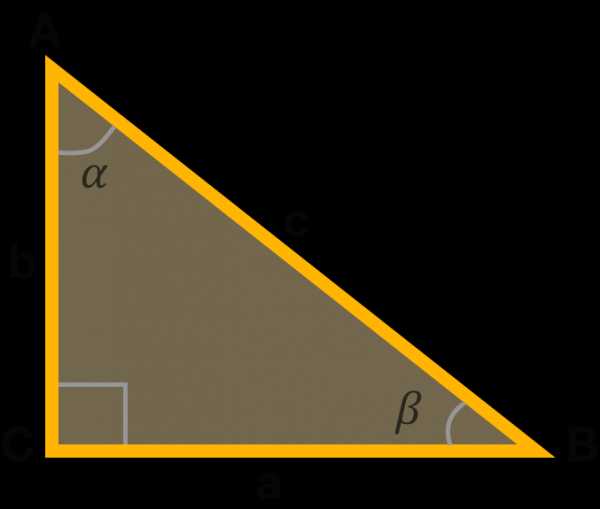Прямоугольный треугольник: стороны a (BC) и b (AC) — катеты, сторона с (AB) — гипотенуза

Прямой угол всегда равен 90°, острый — всегда меньше, а тупой — больше 90°

Согласно теореме косинусов, что бы рассчитать угол α или β, нужно знать длину гипотенузы (АВ) и прилежащий к этому углу катет.

Косинус — это отношение прилежащей стороны к гипотенузе:

• cos α = b деленное на с;
• cos β = а(BC)/с(AB) .

То есть, если вам нужно узнать, например, какой высоты делать крышу над домом, если известна ширина дома и угол наклона крыши, что бы снег не задерживался, то высоту конька рассчитать не составит труда, применяя теорему косинусов. Нужно помнить, что такие функции, как косинусы и синусы в формулах зависят от угла. Синус работает с противолежащей стороной, косинус с работает прилежащей.

Это тригонометрические формулы для вычисления углов в треугольнике через тригонометрические функции синус, косинус, тангенс, котангенс

Косинус — отношение прилежащего катета к гипотенузе

Если треугольник не прямоугольный, его параметры также можно рассчитать, используя теорему Евклида. Суть ее в том, что треугольник, лежащий на плоскости, и имеющий стороны а, b, с, а также углом α, который находится напротив стороны а, может быть рассчитан по следующей формуле:

а²= b²+с²-2²· b· cos α или:

Отсюда можем найти cos α, cos α =( b²+2²- а²) : 2bс.

Небольшое уточнение: если угол α менее 90°, тогда b²+2²- а² > 0, если α =90°, то b²+2²- а²=0, если α >90°,то есть угол тупой, то и b²+2²- а²< 0.

То же самые расчеты делаем для других углов треугольника:

• с² = а² + b² — 2аb cosγ,
• b² = а² + с² — 2ас cosβ.

Как рассчитать косинус угла без формул

Есть некоторые углы, рассчитать косинус которых можно без формул, применяя таблицу синусов и косинусов π. В ней расчет идет через число π, которое делится на целое число, в зависимости от размера угла, то есть sin 30° = π : 6 или 0,5, cos 30° = √3: 2. В такой таблице есть данные косинуса 30 градусов, косинуса 45 градусов, косинуса 60 градусов, косинуса 90 градусов, косинуса 120 градусов, косинус 180 градусов, косинус 270 градусов, косинус 360 градусов, косинус 0, а также аналогичные значения синусов.

Ниже приведена таблица косинусов, дополнительно указаны синусы в их числовом выражении.

Значение угла α (градусов)	Значение угла α в радианах	COS (косинус)
Косинус 0 градусов	0	1
Косинус 15 градусов	π/12	0.9659
Косинус 30 градусов	π/6	0.866
Косинус 45 градусов	π/4	0.7071
Косинус 50 градусов	5π/18	0.6428
Косинус 60 градусов	π/3	0.5
Косинус 65 градусов	13π/36	0.4226
Косинус 70 градусов	7π/18	0.342
Косинус 75 градусов	5π/12	0.2588
Косинус 90 градусов	π/2	0
Косинус 105 градусов	5π/12	-0.2588
Косинус 120 градусов	2π/3	-0.5
Косинус 135 градусов	3π/4	-0.7071
Косинус 140 градусов	7π/9	-0.766
Косинус 150 градусов	5π/6	-0.866
Косинус 180 градусов	π	-1
Косинус 270 градусов	3π/2	0
Косинус 360 градусов	2π	1

Калькулятор расчета косинуса онлайн

Примеры решения задач по геометрии по нахождению неизвестных величин с применением таблицы косинусов Брадиса

Пример 1: Для примера решим следующую задачу. Берем прямоугольный треугольник, у него нужно найти оба угла, но известны гипотенуза с = 12 см, сторона b = 9,2 см. По теореме косинусов cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.

Но наше значение меньше табличного на 0,0006, что становит 3′. Тогда мы вычитаем эту поправку 3′, 39°54′ — 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° — (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа.

1. по формуле а²= b²+с²-2²· b· cos α находим сторону а;
2. по формуле cos β=sinα = а: с, а = с · cos β.

Второй вариант немного проще в вычислении. Обращаемся к таблице Брадиса снова. У нас ближайшее значение 50° 06′ = 0,6414. Поправка на 3′ составляет 0, 0007. Тогда 0, 6414 + 0,0007 = 0,6421.

По условию с = 12 см, тогда а = 12 · 0,6421 = 7,7 см. Задача решена. Если значения углов простые, таблица косинусов и синусов может упростить вычисление. Можно использовать следующие тождества: sin (90°+15°) = cos 15°= cos (90°-75°) = sin 75° Функции повторяются, только нужно учитывать знак. Если нужно найти косинус 145 градусов, находим угол до 90 градусов. 180 °– 145° = 35°. Косинус 35 градусов будет 0,8192 по таблице, если это 145°, это будет значение с отрицательным значением -0,8192.

Пример 2: Рассмотрим треугольник с произвольными углами, ни один из которых не равен 90°. Мы имеем две стороны с =12 см, b = 8,2 см, а также угол α, который равен 31°12′. Найти третью сторону. Формула, которая применялась в предыдущей задаче, не подходит, так как у нас треугольник не прямоугольный (по крайней мере мы это ещё не рассчитали). Используем формулу из теоремы косинусов:

а² = b²+с²-2²· b· cos α. Косинус угла находим на пересечении угла 31° и 12′. Он равен числу 0,8554, которое мы и подставляем в формулу.

а² = 67, 24 + 144 -4 · 8,2 · 0,8554 = 211,24 — 28,07 = 183,17. Находим а = √183,17 = 13, 54 (см)

Если будет стоять задание найти ещё и углы треугольника, используем формулу:

с² = а² + b² — 2аb cos γ, отсюда cos γ = (b² + а² — с²): 2 bс. cos γ = (8,2² + 13,54² — 12²): 2· 8,2·12 = (64,24 + 183, 17 – 144): 196,8 = 0, 5255. Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол:

180° — 58° 18′-31°12′ =89° 30′. Задача решена!

Можно не рассчитывать самому, а использовать сервис и высчитать косинус онлайн, когда регистрируешься на сайте, и любое вычисление приходит автоматически. Минус такого сервиса, его нельзя применять на экзамене по математике. В качестве справочного материала таблицы предоставляются. Естественно, надо хорошо уметь ими пользоваться, так как на экзамен отводится ограниченное количество времени.

COS	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	1′	2′	3′
COS	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	1′	2′	3′
90°											0.0000
89°	0.0000	17	35	52	70	87	105	122	140	157	175	3	6	9
88°	175	192	209	227	244	262	279	297	314	332	349	3	6	9
87°	349	366	384	401	419	436	454	471	488	506	523	3	6	9
86°	523	541	558	576	593	610	628	645	663	680	698	3	6	9
85°	698	715	732	750	767	785	802	819	837	854	0.0872	3	6	9
84°	0.0872	889	906	924	941	958	976	993	1011	1028	1045	3	6	9
83°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	3	6	9
82°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	3	6	9
81°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	3	6	9
80°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	3	6	9
79°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	3	6	9
78°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	3	6	9
77°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	3	6	9
76°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	3	6	8
75°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	3	6	8
74°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	3	6	8
73°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	3	6	8
72°	2942	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	3	6	8
71°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	3	6	8
70°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	3	5	8
69°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	3	5	8
68°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	3	5	8
67°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	3	5	8
66°	3097	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	3	5	8
65°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	3	5	8
64°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	3	5	8
63°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	3	5	8
62°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	3	5	8
61°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	3	5	8
60°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	3	5	8
59°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	3	5	8
58°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	2	5	7
57°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	2	5	7
56°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	2	5	7
55°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	2	5	7
54°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	2	5	7
53°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	2	5	7
52°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	2	5	7
51°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	2	5	7
50°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	2	4	7
49°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	2	4	7
48°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	2	4	7
47°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	2	4	6
46°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	2	4	6
45°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	2	4	6
44°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	2	4	6
43°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	2	4	6
42°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	2	4	6
41°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	2	4	6
40°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	2	4	6
39°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	2	4	6
38°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	2	4	5
37°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	2	4	5
36°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	2	3	5
35°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	2	3	5
34°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	2	3	5
33°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	2	3	5
32°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	2	3	5
31°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	2	3	5
30°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	1	3	4
29°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	1	3	4
28°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	1	3	4
27°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	1	3	4
26°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	1	3	4
25°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	1	3	4
24°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	1	2	4
23°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	1	2	3
22°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	1	2	3
21°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	1	2	3
20°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	1	2	3
19°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	1	2	3
18°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	1	2	3
17°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	1	2	3
16°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	1	2	2
15°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	1	2	2
14°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	1	1	2
13°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	1	1	2
12°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	1	1	2
11°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	1	1	2
10°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	1	1	2
9°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	0	1	1
8°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	0	1	1
7°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	0	1	1
6°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	0	1	1
5°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	0	1	1
4°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	0	0	1
3°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	0	0	0
2°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	0	0	0
1°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	0	0	0
0°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0	0	0
	1.0000

themechanic.ru

cos 120

Доброй ночи! Очень интересный вопрос, надеюсь, мы сможем Вам помочь.  Нам с вами нужно найти cos 120 градусов.
Чаще всего для решения таких задач нужно определить показатели косинуса либо же синуса. Для углов от 0 до 360 градусов практически любое значение cos или sin можно с лёгкостью  найти в соответствующих табличках, которые существуют и распространены. Но что же нам делать, когда в задании просят найти другие величины, которые никак не отражаются в известных таблицах? Далее мы рассмотрим с Вами пример, как найти косинус 120 градусов.
Первым делом мы с Вами вспомним, что синусоида имеет периодичность в графике. Это значит, что определённые участки будут повторяться каждые 180° или через каждые 2пи. А теперь уж подумаем, как мы можем разложить наш косинус 120 градусов, да и таким образом, чтоб получившиеся значения мы легко могли найти в таблице. 

   

cos суммы, как мы вспомним, раскладывается по формуле: произведение cos каждого угла в сумме минус произведение sin каждого угла в сумме: 

   

Теперь давайте попробуем разложить наш cos 120 по этой формуле:

   

 

   

 

   

Надеюсь, данная информация будет для Вас полезна и в дальнейшем, так как благодаря такой схеме можно вычислять значения любых углов.

Ответ: 

ru.solverbook.com

Косинус 120 | Треугольники

Косинус 120 градусов найдем, пользуясь формулой приведения для косинуса тупого угла от 90 до 180 градусов.

Утверждение:

   

Доказательство:

На единичной окружности косинус угла альфа — это абсцисса точки, полученной при повороте на угол альфа относительно точки О из точки (1;0).

Для косинуса тупого угла от 90 до 180 градусов верна следующая формула приведения:

   

Представим 120 градусов как

   

Теперь воспользуемся записанной выше формулой приведения и значением косинуса 60 градусов:

   

Что и требовалось доказать.

Если перевести 120 градусов в радианы, получим

   

Значит, косинус двух пи на три равен

   

Значения тригонометрических функций

www.treugolniki.ru

Таблица косинусов | Cubens

Таблица косинусов — значения косинусов углов записаны в таблицу от 0° до 360°.

Используя таблицу косинусов вы сможете провести расчеты даже если под рукой не окажется инженерного калькулятора.

Чтобы найти значение косинуса нужного вам угла достаточно воспользоваться данной таблицей.

Таблица косинусов в радианах

Таблица косинусов — наровне с таблицей синусов изучается в самом начале тригонометрии. Без понимания таблицы косинусов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.

Тригонометрические функции имеют большое практическое значение в геометрии. Является по сути лишь показателями отношения различных сторон прямоугольного треугольника друг к другу, они способны помощь в решении большинства задач, результат которых сводится к решений прямоугольных треугольников.

Одной из основных тригонометрических функций является косинус. Поэтому в данной таблице косинусов вы сможете найти любое значение косинуса.

Таблица косинусов углов от 0° до 180°

cos(0°) = 1 cos(1°) = 0.999848 cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0.71934 cos(45°) = 0.707107

cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0.069756 cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0

cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0.587785 cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107

cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0.965926 cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1

Косинус 0 (косинус нуля)

равна (равен единице)

Косинус 1 (косинус единицы)

равна

Косинус 3 (косинус трех)

равна

Косинус 90 (косинус 90 градусов)

= 0 (равна нулю)

Косинус 30 (косинус 30 градусов)

равна  

Косинус 45 (косинус 45 градусов)

равна

Косинус 60 (косинус 60 градусов)

равна  

 

Таблица косинусов углов от 181° до 360°

cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.939693 cos(201°) = -0.93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107

cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.515038 cos(240°) = -0.5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0

cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.156434 cos(280°) = 0.173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107

cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.766044 cos(321°) = 0.777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1

Кроме таблицы косинусов, на нашем сайте вы можете просмотреть таблицу синусов, таблица тангенсов, таблица котангенсів.

cubens.com