3.5. Действительные числа
В математике существуют различные построения теории действительного числа:
— по Дедекинду (построение действительного числа с помощью сечений на множестве рациональных чисел),
— по Вейерштрассу (представление действительного числа как бесконечного десятичного ряда),
— по Кантору (построение действительного числа с помощью фундаментальных последовательностей рациональных чисел)…
Но эти построения весьма сложны (не случайно в математике они оформились во второй половине 19 века).
Понятие «действительное число» (как и понятие «бесконечная десятичная дробь»), основные положения теории действительного числа вполне доступны учащимся 7 класса. В настоящее время существует тенденция более раннего изучения действительных чисел, что ускоряет создание цельной системы знаний учащихся о числе, облегчает потребности практики вычислений, позволяет строже изложить некоторые вопросы фундаментальной теории…
Понятие «иррациональное число» появляется в учебниках 8 класса.
Мотивация введения действительных чисел опирается на внутренние потребности математики, а не на практику. Учащиеся убеждаются в необходимости введения новых чисел при решении следующих задач:
— Решить уравнение: х2 = 2.
— Найти отношение длины дуги окружности к ее диаметру.
— Найти сторону квадрата, если его площадь 3 см2.
— Решить графически уравнение: х2 = 3.
— К множеству каких чисел относятся числа 2, 56565…; 7,23233233…; 0, 123123412345…?
Определение иррационального числа дается через отрицание.
Пример: Алгебра – 8(С.А. Теляковский)
Доказывается, что «среди рациональных чисел нет такого числа, квадрат которого равен 2».
Вводится понятие «действительное число»: «Если к положительным бесконечным десятичным дробям присоединить противоположные им числа и нуль, то получим множество чисел, которые называют действительными числами».
Дается определение иррациональных чисел: «Каждую бесконечную десятичную периодическую дробь можно записать в виде отношения m /n, где m – целое число, n – натуральное число. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает отрицание). Иррациональные числа нельзя представить в виде отношения m /n. Таким образом, множество действительных чисел состоит из рациональных и иррациональных чисел
Приводятся примеры иррациональных чисел.
Вводятся «действия» над числами. В школьном курсе действия с иррациональными числами сводятся к операциям с их рациональным приближениями по недостатку и по избытку5.
Остановимся более подробно на методике изучения иррациональных чисел.
Рациональные и иррациональные числа
В 5 – 6 классах учащиеся познакомились с обыкновенными дробями. Перед изучением иррациональных чисел целесообразно обобщить эти знания и на новом уровне рассмотреть множество рациональных чисел Q.
В множестве натуральных чисел N операция деления имеет ограниченный характер: если а и в натуральные числа, то не всегда найдется натуральное число х такое, чтобы
ах = в (приведите примеры). Другими словами, в том случае, когда в не делится нацело на а, уравнение ах = в неразрешимо. Чтобы устранить это несовершенство, вводятся дроби, записываемые в виде отношения m/n, где m,n – натуральные числа. При этом число m называют числителем, а число n знаменателем дроби m/n. Вспомним правила действий с дробями:
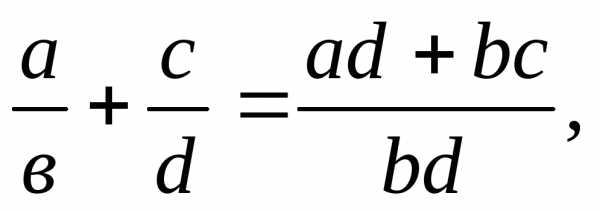
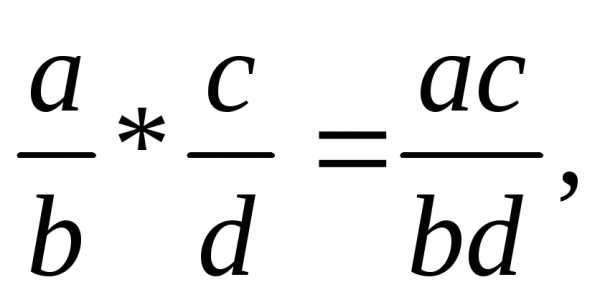
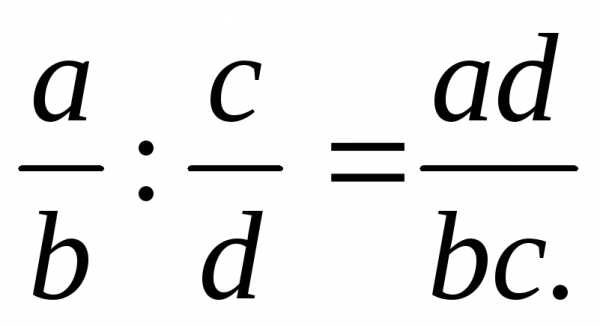 (1)
(1)
Правило 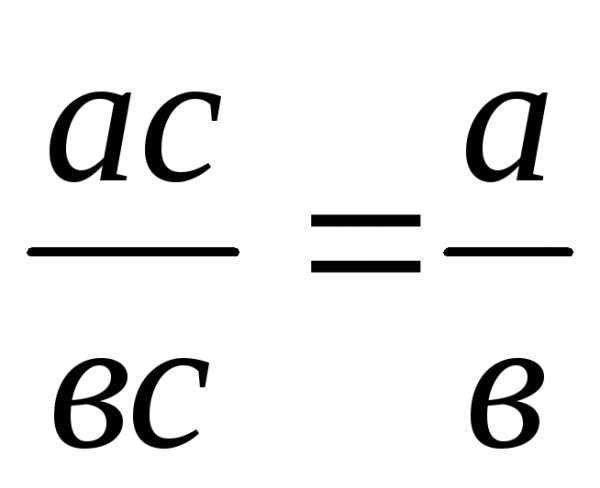 позволяет «сокращать» дробь на общий
для числителя множитель. Например,
позволяет «сокращать» дробь на общий
для числителя множитель. Например,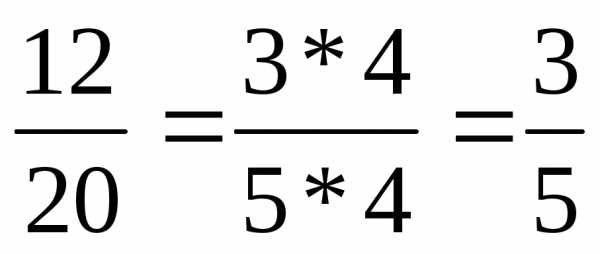 . Как видим, равные дроби могут очень
различаться по внешнему виду. (Убедитесь,
что дроби
. Как видим, равные дроби могут очень
различаться по внешнему виду. (Убедитесь,
что дроби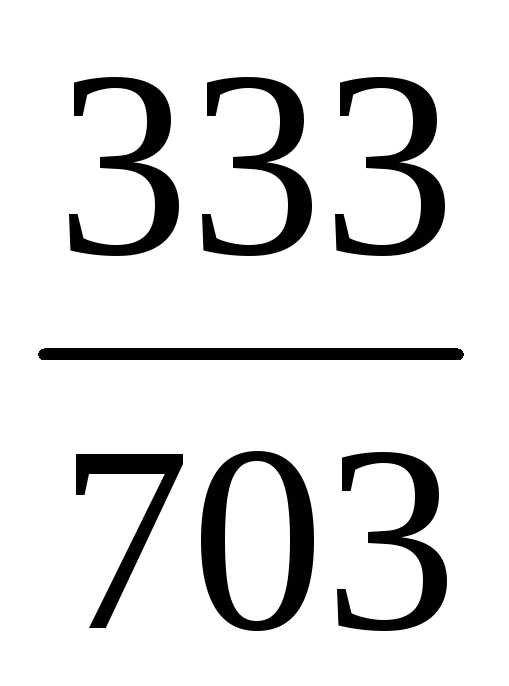
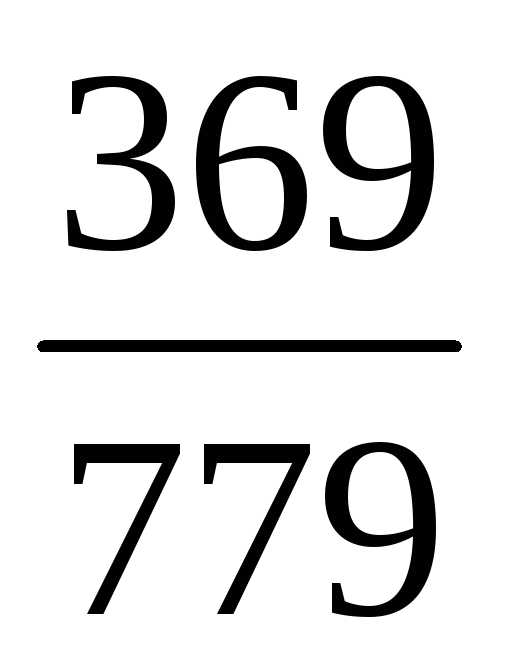 — равные дроби.) Натуральное числоn можно считать частным случаем дроби,
отождествляя его с
— равные дроби.) Натуральное числоn можно считать частным случаем дроби,
отождествляя его с 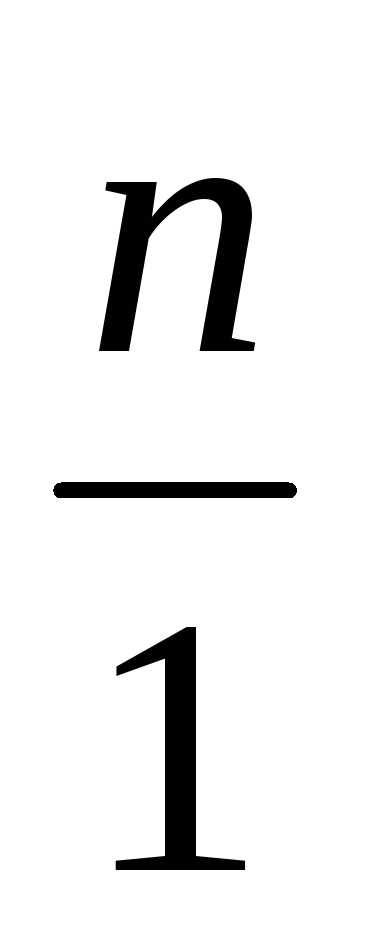 .
. Построенное
расширение натурального ряда обозначим
через Q+ — это положительные
рациональные числа (от латинского ratio
— отношение). Умножение в Q+ ассоциативно и коммутативно, уравнения
вида ах = в,
где а и в – любые числа из Q+,
разрешимы (решением будет х =
положительные
рациональные числа (от латинского ratio
— отношение). Умножение в Q+ ассоциативно и коммутативно, уравнения
вида ах = в,
где а и в – любые числа из Q+,
разрешимы (решением будет х =  ).
Следовательно, (Q+,.)
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
).
Следовательно, (Q+,.)
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
Если ноль и отрицательные числа сначала появились как математические абстракции и лишь впоследствии нашли им содержательное толкование, то дроби были известны с древнейших времен:
— Распределение некоторого общего достояния на индивидуальные доли было повседневной практикой (см., например, в библейской книге Чисел стихи 25 – 46 главы 31).
— Другим видом деятельности, приводившим к дробям, были измерения: если, например, стандарт длины не укладывался между двумя данными точками целое число раз, приходилось прибегать к более мелким его частям6
Присоединяя к
положительным рациональным числам
противоположные им величины и ноль,
получаем все множество рациональных
чисел Q.
Оно состоит, таким образом, из нуля,
положительных и отрицательных целых
чисел, положительных и отрицательных
дробей. Сложение, умножение и деление
в Q
выполняются по формуле (1), вычитание
осуществляется по правилу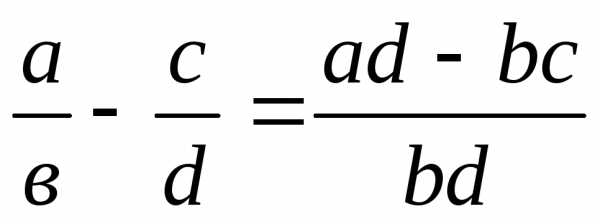
(Выполните действия
с рациональными числами: 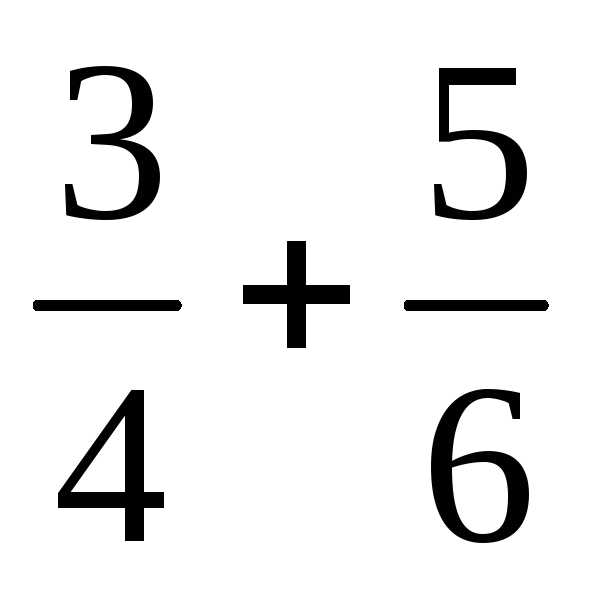 ,
,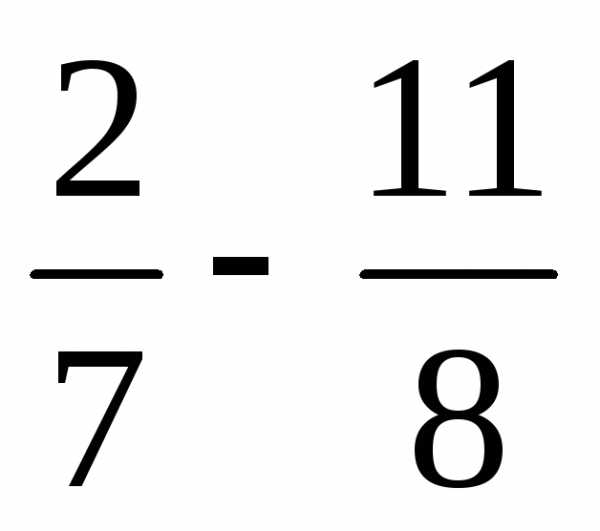 ,
—
,
—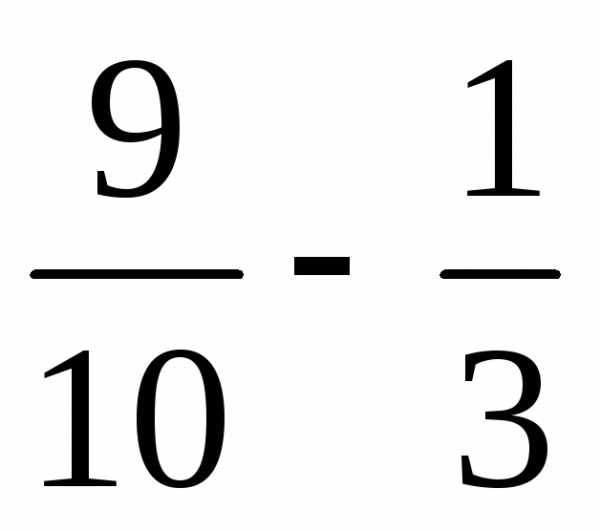 ….
)
….
)
В множестве Q
рациональных чисел все четыре
арифметических операции выполняются
беспрепятственно за одним досадным
исключением: нельзя делить на ноль (один
из доводов в пользу того, что 0 –«ненастоящее»
число). Следовательно, в этом множестве
разрешимы уравнения вида а
+ х = в при
любых а, в и уравнения вида ах
= в при всех а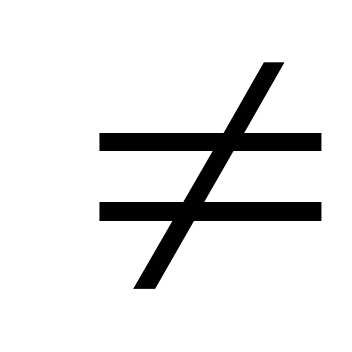 0
и при всехв.
Таким образом, множество Q
является кольцом,
а его ненулевые элементы образуют
коммутативную группу по умножению.
Кольца, обладающие этим свойством,
называются полями.
0
и при всехв.
Таким образом, множество Q
является кольцом,
а его ненулевые элементы образуют
коммутативную группу по умножению.
Кольца, обладающие этим свойством,
называются полями.
Поле рациональных чисел бесконечно, но существуют и конечные поля. Таковым будет, например, любое кольцо Zp остатков от деления натуральных чисел на простое число p. Имея перед собой таблицу умножения поля Z5, легко решить в нем уравнения
2х = 1, 3х = 4, 4х= 5. А вот в кольце Z6 эти уравнения не имеют корней.
В поле рациональных чисел разрешимо любое уравнение ах + в = 0,решением будет
х = —  .
Поле рациональных чисел всюду плотно,
так как между любыми двумя рациональными
числамиr1и r2
.
Поле рациональных чисел всюду плотно,
так как между любыми двумя рациональными
числамиr1и r2
Наглядное
представление о рациональных числах
дает координатная ось. На некоторой
прямой линии выбирается точка 0 – начало
отсчета, указывается единица масштаба,
направление. Если дано положительное
рациональное число 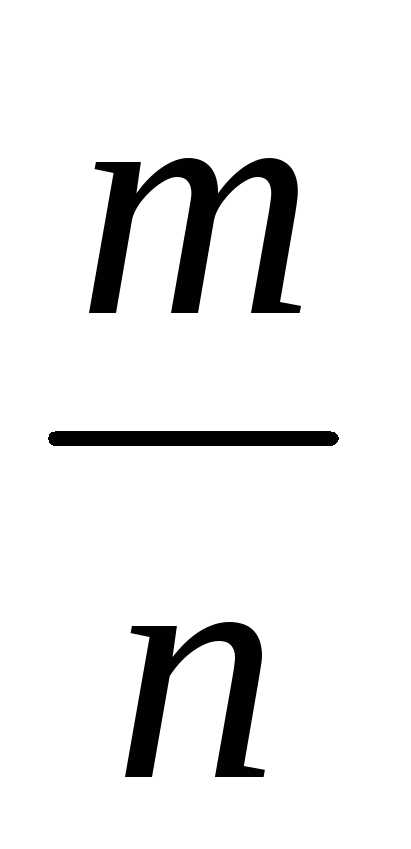 ,то
единица масштаба делится на n равных частей и вправо от нуля эта доля
откладывается m раз. Полученная точка и есть изображение
числа
,то
единица масштаба делится на n равных частей и вправо от нуля эта доля
откладывается m раз. Полученная точка и есть изображение
числа 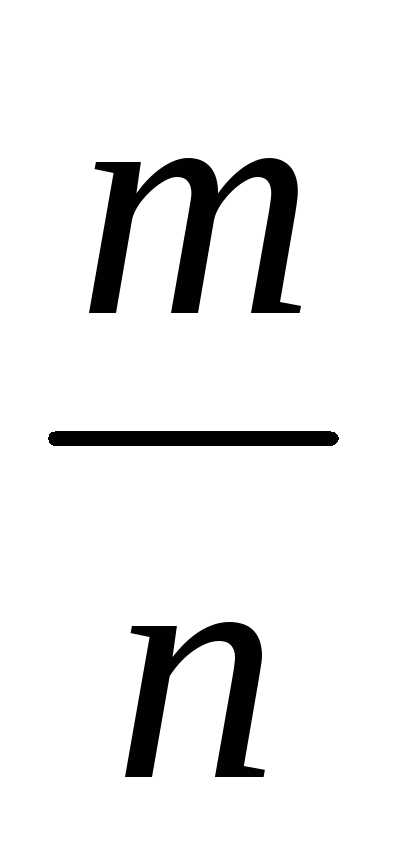 .
Если число отрицательное – откладывание
производят влево от нуля. Например,
.
Если число отрицательное – откладывание
производят влево от нуля. Например,
-2/3 5/3
——!—.—.—!—.—.—!—.—.—!———>
-1 0 1 2
Построив числовое множество Q (поле рациональных чисел), в котором разрешимо любое линейное алгебраическое уравнение ах + в =о, естественно перейти к исследованию квадратных уравнений ах2 + вх + с = 0. В простейшем случае х2 – 1 = 0, т.е. х2 = 1, имеет два решения (корня): х1 =1, х2 = -1. Однако уже следующий напрашивающийся шаг заводит нас в тупик.
Теорема 1. Уравнение х2 = 2 не имеет решений в поле рациональных чисел.
Теорема 2. Диагональ квадрата несоизмерима с его стороной.
Необходимо самостоятельно познакомиться с доказательствами этих теорем, приводимыми авторами школьных учебников.
Т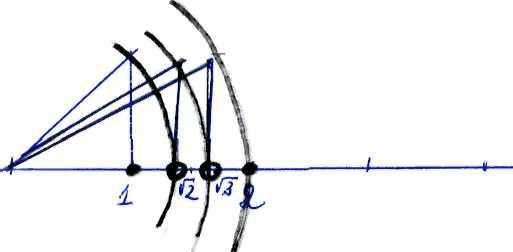
Рис. 1.
еоремы 1 и 2 при всем внешнем несходстве представляют собой лишь разные интерпретации одного и того же математического факта: одна на языке алгебры, другая — в геометрических терминах. (В математике это обычное явление.) Обратимся теперь к координатной оси. Если взять на ней точки, соответствующие рациональным числама и в (пусть а < в), то середина отрезка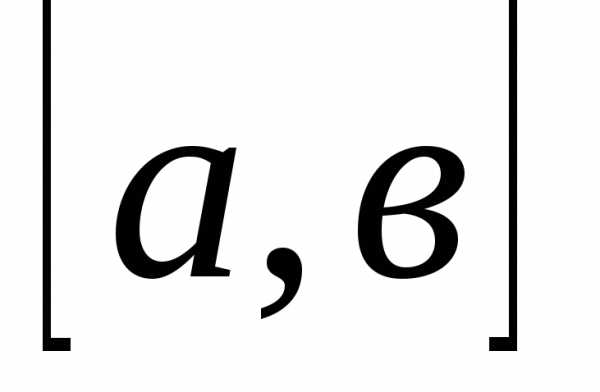 выражается
числомс = (а + в): 2.
Это тоже рациональное число, так что
между любыми двумя рациональными числами
лежит еще одно. Деля пополам отрезки
выражается
числомс = (а + в): 2.
Это тоже рациональное число, так что
между любыми двумя рациональными числами
лежит еще одно. Деля пополам отрезки 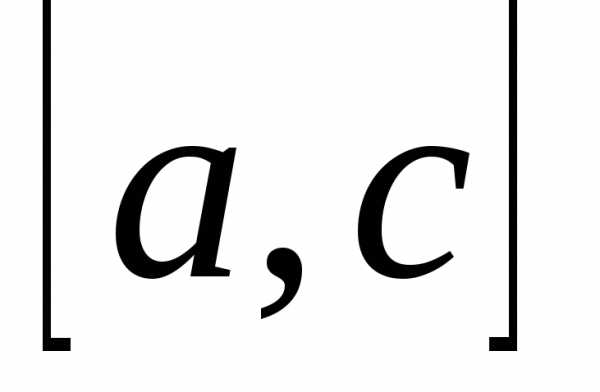 и
и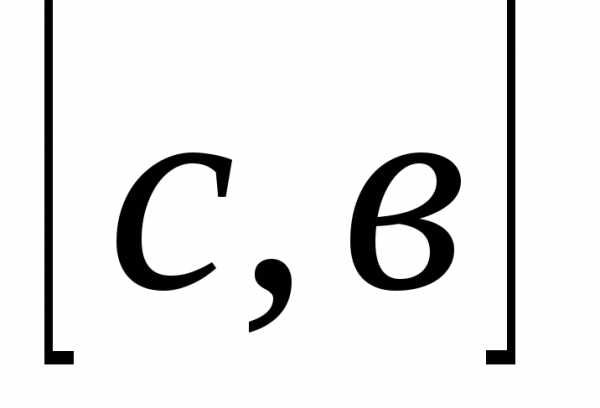 ,
получим еще два рациональных числа
междуа и в и т.д. Поскольку этот процесс деления
пополам (дихотомия) можно продолжать
неограниченно, приходим к выводу, что
между произвольными рациональными
числами а и в находится
бесконечно много других рациональных
чисел. Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка
,
получим еще два рациональных числа
междуа и в и т.д. Поскольку этот процесс деления
пополам (дихотомия) можно продолжать
неограниченно, приходим к выводу, что
между произвольными рациональными
числами а и в находится
бесконечно много других рациональных
чисел. Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка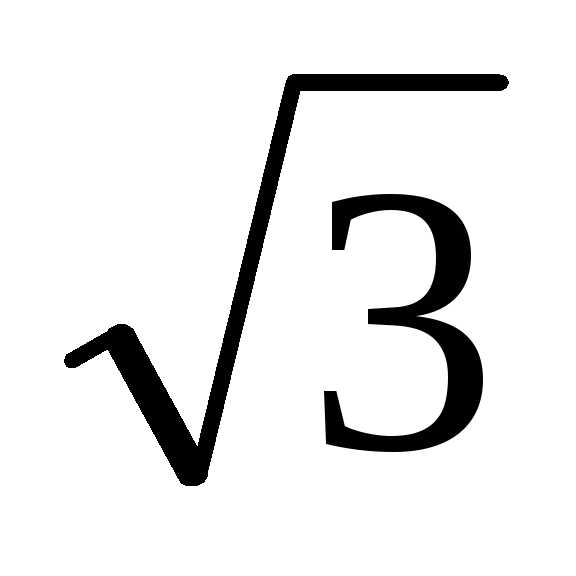 .
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.)
.
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.) Иррациональных
чисел тоже бесконечно много: если  —
иррациональное, аа – рациональное число, то сумма
—
иррациональное, аа – рациональное число, то сумма 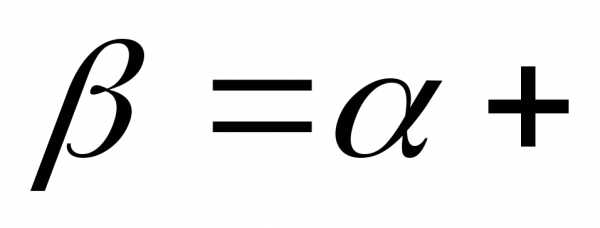 а
и произведение
а
и произведение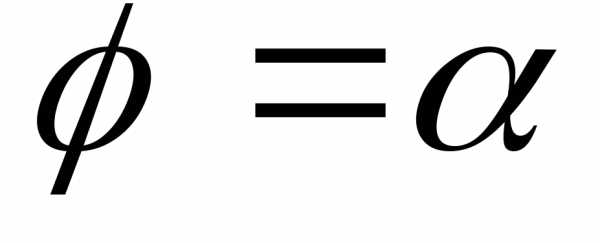 а
(при а
а
(при а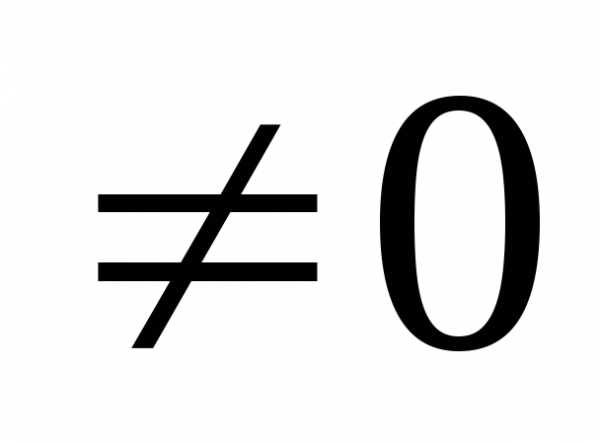 )
тоже будет иррациональное число (иначе,
например,
)
тоже будет иррациональное число (иначе,
например,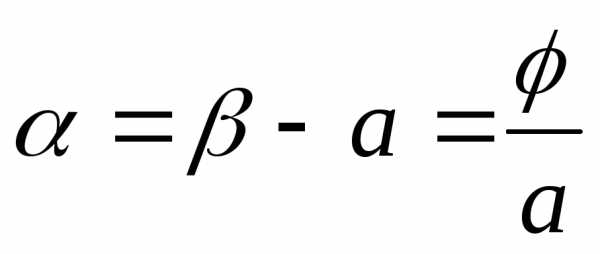 оказалось бы рациональным).
оказалось бы рациональным).
Первый конкретный
пример иррационального числа – это
длина диагонали единичного квадрата,
т.е. положительный корень уравнения х2 = 2, обозначаемый
через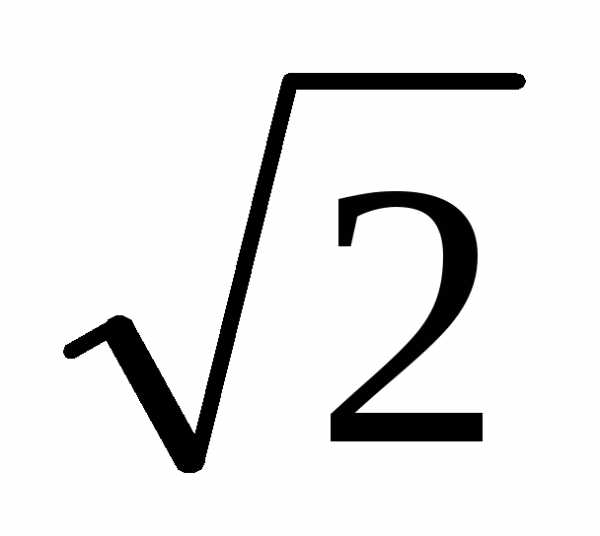 .
Рассуждения, проведенные в доказательстве
теоремы 1, могут быть дословно повторены
и для уравнений х2 = 3, х3 =5, что доказывает иррациональность
чисел
.
Рассуждения, проведенные в доказательстве
теоремы 1, могут быть дословно повторены
и для уравнений х2 = 3, х3 =5, что доказывает иррациональность
чисел 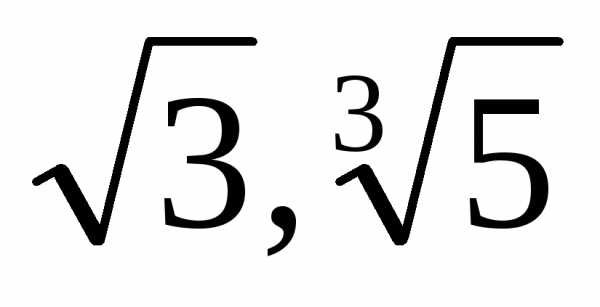 .
.
Изобразив действительные числа на координатной прямой, мы получим, что каждой точке координатной прямой соответствует действительное число (прямая без «дырок») и каждому действительному числу отвечает точка на прямой. Координатная прямая, на которой изображено множество действительных чисел, называется числовой прямой, поле действительных чисел стало непрерывным, то есть отношения и алгебраические операции с действительными числами сводятся к одноименным отношениям и операциям с их рациональными приближениями по недостатку и избытку.
После введения
действительных чисел появилась
возможность дать общую запись для
решений любого квадратного уравнения ах2 + вх + с = 0 с
использованием радикала (знака извлечения
корня), а именно х = 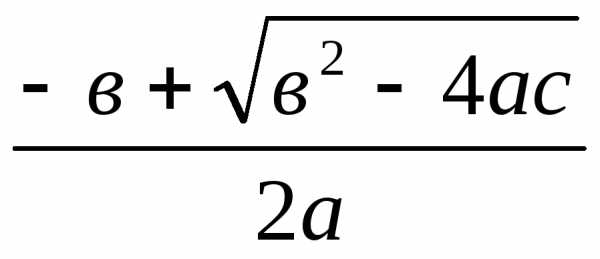 или х =
или х = .
.
Если величина D = в2— 4ас (дискриминант) положительна, уравнение имеет два корня, рациональных или иррациональных в зависимости от того, является дискриминант полным квадратом или нет.
Золотым сечением
называется деление отрезка длины 1 на
две части, большая из которых х является средней пропорциональной
величиной между всем отрезком и его
меньшей частью 1
– х, то есть
принцип золотого сечения (название ввел
Леонардо да Винчи в конце 15 века)
составлял, в частности, теоретическую
основу архитектурных композиций
классической древности и эпохи
Возрождения. Для нахождения х необходимо решить квадратное уравнение х2 + х – 1 = 0,
откуда х = 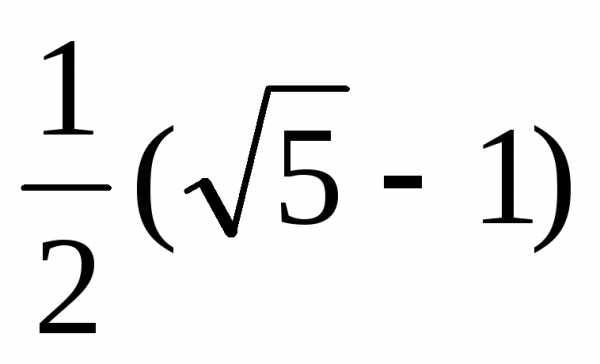 (отрицательный
корень отбрасываем). Для нас иррациональность
этого числа очевидна, в древности же
она была установлена весьма сложным
путем, а сам факт её существования
произвел удручающее впечатление.
(отрицательный
корень отбрасываем). Для нас иррациональность
этого числа очевидна, в древности же
она была установлена весьма сложным
путем, а сам факт её существования
произвел удручающее впечатление.
Пример квадратного уравнения возбудил надежду на то, что алгебраические уравнения и всех других, более высоких степеней, окажутся разрешимыми в радикалах, то есть корни можно будет выразить с помощью арифметических операций и извлечения корней. В середине 16 века итальянские математики Тарталья, Кардано и Феррари нашли подобные формулы для кубического уравнения четвертой степени. (Происходило это в атмосфере ожесточенной полемики о приоритете, с публичными состязаниями в решении соответствующих задач, проклятиями и покаяниями.) В почти три последующие столетия существенных продвижений в этом вопросе не было, и лишь в 1826 году норвежский математик Нильс Хенрик Абель (1802 – 1829) доказал, что для каждого натурального числа n>4 существует алгебраическое уравнение n степени с целыми коэффициентам, неразрешимыми в радикалах (например, х5 – 4х – 2 = 0). Окончательное решение проблемы, занимавшей умы лучших математиков, принадлежит французу Эваристу Галуа (1811 – 1832). Он ввел понятие группы и показал, что каждому алгебраическому уравнению соответствует некоторая группа, по свойствам которой и можно судить, разрешимо или нет уравнение в радикалах.
Н. Абель и Э. Галуа ушли из жизни совсем молодыми (первый скончался от туберкулеза, второй был убит на дуэли), их идеи не были должным образом восприняты современниками, но впоследствии оказали огромное влияние на развитие важнейших разделов математики. Имена этих выдающихся ученых носят многие математические объекты, например, абелевыми называются коммутативные группы, а конечные поля – полями Галуа.
Задания к лекции
Путь построения числового множества в науке отличается от соответствующего пути, принятого в школьной математике. Укажите эти отличия, вскройте их причины.
Проанализируйте методический подход к введению модуля числа, данный в учебниках математики Н.Я. Виленкина. Сравните этот подход с другими, встречающимися в методической и учебной литературе.
3. Познакомьтесь с операциями на множестве Rи разработайте беседу для учащихся 9 класса на тему «Отношения и операции на множестве действительных чисел».
4.Подберите материал и наметьте план беседы для учащихся 9 класса о развитии понятия числа.
Указание1. Большую роль в беседе следует отвести историческим сведениям о развитии понятия числа. 2. Постарайтесь аргументированно обосновать необходимость расширения числовых множеств, показывая при этом потребности практики и науки.
5. Сделайте обзор литературы, которая может быть использована а) учителем для проведения элективного курса по изучению комплексных чисел, б) учеником для самостоятельного чтения при изучении комплексных чисел.
studfiles.net
Действительные числа
Действительные числа
Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел. Множество всех действительных чисел обозначают буквой R. Очевидно, что R.
Основные свойства действительных чисел:
множество действительных чисел упорядоченное, то есть для каждых двух различных действительных чисел иможно указать, какое из них меньшее;
множество действительных чисел всюду плотное, то есть между каждыми двумя действительными числами исуществует еще по крайней мере одно действительное числоа следовательно, и бесконечное множество действительных чисел;
множество действительных чисел непрерывно, то есть в множестве действительных чисел нет ни скачков, ни пробелов, а геометрически это означает, что каждому действительному числу на числовой прямой соответствует точка, имеющая координату, и, обратно, каждая точка числовой прямой имеет действительную координату;
арифметические действия над действительными числами всегда возможны (кроме деления на нуль) и в результате дают действительное число.
Множество действительных чисел R дополняют двумя элементами, обозначаемыми (плюс и минус бесконечность). При этом полагают, что
Но операции не определены. Кроме того, для любого числа полагают, что справедливо неравенство
и справедливы операции
для
для
Операции не определены. Бесконечности называют иногда «бесконечными числами» в отличие от действительных чисел, которые называют «конечными числами». В дальнейшем под числом будем понимать конечное число.
Определение 1. Абсолютной величиной, или модулем, действительного числа называют неотрицательное число обозначаемоеи определяемое следующим образом:
Ясно, что . Еслито это эквивалентно тому, что. Для любых действительных чиселисправедливы следующие соотношения:
Определение 2. Подмножество множества всех действительных чиселназываетсяограниченным снизу, если существует действительное число такое, что оно не больше каждого числаизX, то есть для любого выполняется неравенство. Числоназывают числом, ограничивающим множествоснизу.
Множество, не являющиеся множеством ограниченным снизу, называют множеством неограниченным снизу. Термин «множество неограниченное снизу» означает, что каково бы ни было отрицательное, сколь угодно большое по абсолютной величине число , в данном множестве обязательно найдется еще меньшее число.
Если множество ограничено снизу числом, и числопринадлежит множеству, то числоназываютнаименьшим или минимальным числом множества Если в множестве есть наименьшее число, то оно единственно.
Пример. а) множество чисел ограничено снизу числом1, причем это число 1 является наименьшим;
б) множество X – множество всех неотрицательных чисел (т.е. чисел, удовлетворяющих неравенству) тоже является ограниченным снизу и его наименьшим значением является число;
в) множество Y – множество всех положительных чисел (т.е. чисел, удовлетворяющих неравенству) тоже является ограниченным снизу числом, но множествоY не имеет наименьшего, так как число не принадлежитY. При этом число является наибольшим из всех чисел, ограничивающих множествоY снизу, а элементы множестваY в силу свойств плотности и непрерывности действительных чисел могут быть сколь угодно близки к числу , оставаясь больше его;
г) множество D – множество всех отрицательных чисел неограниченно снизу, так как какое бы отрицательное число ни взять, найдется еще меньше число.
Определение 3. Подмножество множества всех действительных чиселназываетсяограниченным сверху, если существует такое число что оно не меньше каждого числато есть для любоговыполняется неравенствоЧислоназывают числом ограничивающим множествосверху.
Множество, не являющееся множеством ограниченным сверху, называют множеством неограниченным сверху. Термин «множество неограниченное сверху» означает, что каково бы ни было сколь угодно большое положительное число , в данном множестве обязательно найдется еще большее число.
Если множество ограничено сверху числомито числоназываютнаибольшим или максимальным числом множества Если есть в множестве наибольшее число, то оно единственное.
Определение 4. Множество, ограниченное и снизу и сверху, называется ограниченным множеством.
Другими словами, множество ограничено, если существуют числатакие, что для каждогосправедливо неравенство:
Множество, не являющееся ограниченным, называют неограниченным.
Пример. а) множество ограничено, т.к. для всякогосправедливо, причем оно имеет и наименьшее значениеи наибольшее;
б) множество — множество положительных чисел, являясь ограниченным снизу, неограниченно сверху,
в) множество — множество всех целых чисел неограниченно как снизу, так и сверху
Ясно, что чисел ограничивающих множество снизу (сверху) может быть много.
Определение 5. Наибольшее число среди всех чисел, ограничивающих снизу множество , называетсянижней гранью (или инфимумом) множества и обозначается через(инфимум — от латинского словаinfimum – наименьший).
Например, для множества — множества всех положительных чисел нижней гранью является число0, а для множества всех натуральных чисел нижней гранью является число1, оно является и наименьшим.
Определение 6. Наименьшее среди всех чисел, ограничивающих сверху множество , называетсяверхней гранью (или супремумом) множества и обозначается через (супремум – от латинского словаsupremum – наибольший).
Например, для множества всех отрицательных чисел число 0 является верхней гранью.
Если в множестве существует наименьшее (наибольшее) число, то оно является нижней (верхней) гранью этого множества. Всякое ограниченное сверху непустое множество имеет верхнюю грань, а всякое ограниченное снизу непустое множество имеет нижнюю грань.
Множество всех действительных чисел , удовлетворяющих двойному неравенству, называютоткрытым промежутком или интервалом и обозначают
Множество всех действительных чисел , удовлетворяющих двойному неравенству, называютзакрытым промежутком или отрезком и обозначают
Пример 5. Примеры числовых множеств:
1. если2.если
3. если4.если
5. если6.если
7. если8.если
9. если10.если
Множества, приведенные под номерами 1 и 2, называют полуоткрытыми промежутками, множества под номерами 3, 4, 5, 6, 7 называют неограниченными промежутками, причем множество под номером 7 есть множество всех действительных чисел R.
Определение 7. Множество всех действительных чисел , удовлетворяющих двойному неравенству, где, называют — окрестностью точки a.
Этот факт можно записать следующим образом Для любых двух неравных действительных чиселсуществуют непересекающиеся- окрестности.
Числовое множество называют симметричным относительно начала координат, если этому множеству вместе с числом принадлежит и ему противоположное число, то есть, если, то и.
Примерами таких множеств являются множества под номерами 7, 8, 9, а так же множество всех рациональных чисел Q и множество и т.д.
Вопросы и задания
1. Записать определения ограниченного снизу, ограниченного сверху, ограниченного множества. Привести примеры таких множеств. Что такое наименьшее (наибольшее) число множества?
2. Дать опеределение нижней грани (инфимума), верхней грани (супремума).
3. Что такое — окрестность точки a? Изобразить на числовой прямой — окрестность точек A(2), В(3) так, чтобы они: а) не пересекались; б) пересекались. Указать возможные значения для каждого из случаев.
4. Перечислить операции с , которые не определены.
5. Даны множества Указать наименьшее и наибольшее числа каждого из множеств: а)б)в)г)
6. Даны множества Указать точные нижние грани (инфимумы) и точные верхние грани (супремумы) множеств: а)б)в)г)Имеют ли эти множества наименьшее и наибольшее числа?
7. Даны множества Имеют ли эти множества точные нижние и верхние грани, наименьшее и наибольшее числа? Если имеют, то указать их.
8. Изобразить на числовой прямой множества, точки которых удовлетворяют следующим соотношениям: а)б)в)
9. Изобразить на числовой прямой множества, точки которых удовлетворяют следующим соотношениям: а)б)в)
6
studfiles.net
Какие числа называются действительными?

В тринадцатое число ему не везло.
Не везло и во все остальные числа.
__Большие и маленькие, длинные и короткие, целые и дробные, рациональные и не очень — все они составляют одно огромное множество — множество действительных чисел. 1 и 100, два и корень из двух, 1.618, 3.14, -12 и даже +100500 – все это действительные числа.
__Давайте же строго научно определим, какие числа называются действительными, а также попытаемся ответить на следующие часто встречающиеся вопросы:
- является ли ноль действительным числом?
- что такое целая часть действительного числа?
- какими свойствами обладает модуль действительного числа?
__На самом деле эти вопросы не такие уж сложные, как может показаться на первый взгляд. Для начала определимся с самим понятием действительного числа.
Определение1: Действительное число (также его часто называют вещественным ) — это любое положительное число, отрицательное число или нуль.
Определение2: Множеством действительных чисел называют объединение множеств рациональных и иррациональных чисел.
Строго Научное Определение:
Положительным действительным (вещественным) числом «α» называют бесконечную десятичную дробь N, n1 n2… nk,… не оканчивающуюся последовательностью девяток.
Отрицательным действительным числом (вещественным) называют бесконечную десятичную дробь вида «α» = — N, n1 n2… nk. . . не оканчивающуюся последовательностью девяток.
__Добавив к отрицательным и положительным действительным числам число 0 получим полное множество действительных чисел. Обратите внимание на нюанс, указанный в Строго Научном Определении. Все дело в том, что любую конечную десятичную дробь N, n1 n2… nk можно записать в виде бесконечной десятичной дроби N, n1 n2… nk 000…0… оканчивающейся «хвостом» из нулей. Например:
1,1=1,1000…000….
При этом дроби 1,1 соответствует последовательность пар десятичных приближений :
(1,1; 1,2) , (1,10; 1,11) , (1,100; 1,101) и т. д. Заметьте, все приближения по недостатку для этой дроби одинаковы 1,1=1,10=1,100=…
Рассмотрим теперь бесконечную десятичную дробь 1,09999…. Для неё последовательность пар десятичных приближений имеет вид (1,09; 1,10), (1,099; 1,100) и т. д.
В этом случае совпадают все десятичные приближения по избытку: 1,10=1,100=…
__Обратите внимание, приближения по недостатку для первой дроби совпадают с приближениями по избытку для дроби второй. Таким образом обе дроби геометрически выражают одну и ту же длину. Именно поэтому, (для того чтобы не обозначать одно и то же число двумя способами ) условились не использовать бесконечных десятичных дробей, оканчивающихся бесконечной последовательностью девяток. Такие дроби всегда можно заменить конечной десятичной дробью, поставив вместо девяток нули и увеличив на 1 цифру, стоящую перед ними. Например :
4,4749999…99..=4,475000…0..
99,999999999…=100,00000000…
Еще один нюанс: последовательность из девяток должна быть именно бесконечной,
99,999 ≠ 100.
Давайте подведем итог.
- Действительным ( иногда его называют вещественным) числом называется любое целое число, а также все конечные и бесконечные дроби.
- Дроби, оканчивающиеся бесконечной последовательностью девяток для удобства использования округляют в большую сторону.
- Различают положительные действительные числа, отрицательные действительные числа и ноль.
- Множество действительных чисел разделяется на множества рациональных и иррациональных чисел.
__Надеюсь вы разобрались с понятием действительного числа и со всеми теми особенностями, которые присущи таким числам. Если же вам по прежнему что-то непонятно — добро пожаловать в Вопрос-Ответник.
Комментирование и размещение ссылок запрещено.
df-dt.com
Действительные числа — это… Что такое Действительные числа?
Веще́ственные, или действи́тельные[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.
Множество вещественных чисел обозначается (Unicode: ℝ) и часто называется вещественной прямой.
Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.
Примеры
Определения
Существует несколько стандартных путей определения вещественных чисел:
Аксиоматическое определение
См. основную статью Аксиоматика вещественных чисел.
Множество вещественных чисел можно определить как топологически полное, упорядоченное поле, то есть поле с отношением , которое удовлетворяет следующим аксиомам:
- Отношение является отношением линейного порядка:
- Порядок согласован со структурой поля:
- Порядок на удовлетворяет условию полноты:
Примечания
Из свойства 3 следует, что у любого непустого ограниченного сверху множества (то есть такого, что для всех x из A все для некоторого ) существует точная верхняя грань (минимальная из всех), то есть число такое, что
- Для всех x из A все
- Если свойству (1) удовлетворяет также число , то .
Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля .
Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)
Пополнение рациональных чисел
Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике .
Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {ri}. На таких последовательностях можно естественным образом ввести арифметические операции: {ri} + {qi} = {ri + qi} и .
Две такие последовательности и считаются эквивалентными , если при .
Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.
Дедекиндовы сечения
См. основную статью Дедекиндово сечение.
Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества A и B такие, что:
- для любых и ;
- B не имеет минимального элемента.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Например, вещественному числу соответствует дедекиндово сечение, определяемое или и и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить мы рассекли множество на две части: все числа, что левее и все числа, что правее ; соотвеетственно, равно точной нижней грани множества B.
Бесконечные десятичные дроби
Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.
Бесконечной десятичной дробью (со знаком) называется последовательность вида , где di являются десятичными цифрами, то есть .
Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где , либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.
Значение десятичной дроби формально задаётся суммой ряда .
Счетность множества
TODO:
Примечания
- ↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.
Ссылки
- Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
- Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.
См. также
Wikimedia Foundation. 2010.
dal.academic.ru
Действительные числа /qualihelpy
Рациональными числами называют числа, которые можно представить в виде обыкновенной дроби , где и . Множество рациональных чисел обозначают .Рациональными являются натуральные и целые числа, а также конечные и периодические десятичные дроби, так как все они могут быть обращены в обыкновенную дробь.
Множество иррациональных чисел состоит из бесконечных непериодических десятичных дробей. Например, иррациональными являются числа: ; ; .Все рациональные и все иррациональные числа образуют множество действительных чисел. Запись обозначает множество всех действительных чисел или множество всех точек числовой прямой.Координаты точек
Рассмотрим прямую, на которой указаны начало отсчета, положительное направление и единичный отрезок. Каждой точке этой прямой соответствует число, которое называют координатой точки на прямой.
Каждой точке координатной плоскости соответствует пара чисел , которые называют координатами точки на плоскости.Изображения числовых множеств
Отрезок – это множество всех действительных чисел, удовлетворяющих неравенству . С другой стороны это множество точек числовой прямой, состоящее из точек и , а также всех точек, находящихся между ними (рис. 1.7). Например, на рисунке 1.8 отрезок есть множество всех действительных чисел, удовлетворяющих неравенству .Например, на рисунке 1.10 интервал есть множество всех действительных чисел, удовлетворяющих неравенству .Полуинтервалы и – множества всех действительных чисел, удовлетворяющих неравенствам и .Например, полуинтервал – это множество всех действительных чисел, удовлетворяющих неравенству (рис. 1.11), а полуинтервал – множество всех действительных чисел, удовлетворяющих неравенству (рис. 1.12).Отрезки, интервалы и полуинтервалы называют промежутками.
Длина отрезка. Чтобы найти длину отрезка, необходимо из координаты конца отрезка вычесть координату его начала, то есть длина отрезка равна . Середина отрезка. Чтобы найти середину отрезка, необходимо найти полусумму координат концов отрезка, то есть серединой отрезка является число .Операции над числовыми множествами
Например, запишем, что число принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел: , .Например, множество натуральных чисел является подмножеством множества рациональных чисел, а множество рациональных чисел – подмножеством множества действительных чисел: и .Примером объединения множеств является решение совокупности неравенств: решением совокупности неравенств является объединение промежутков и . Примером пересечения множеств является решение системы неравенств: решением системы неравенств является пересечение промежутков и .helpy.quali.me
4. Действительные числа
Одним из источников появления десятичных дробей является деление натуральных чисел, другим — измерение величин. Выясним, например, как могут получиться десятичные дроби при измерении длины отрезка.
ПустьX — отрезок, длину которого надо измерить, е — единичный отрезок. Длину отрезка х обозначим буквой
X, а длину отрезка е — буквой Е. Пусть отрезок х состоит из n отрезков, равных е, и отрезка х1, который короче отрезка е т.е. n∙Е<X<(n+1)∙Е. Числа n и n+1 есть приближенные значения длины отрезка х при единице длины Е с недостатком и с избытком с точностью до 1.
Чтобы получить ответ с большей точностью, возьмем отрезок е1 — десятую часть отрезка е и будем укладывать его в отрезке х1. При этом возможны два случая.
1) Отрезок ех уложился в отрезке х1 точно n раз. Тогда длина n отрезка х выражается конечной десятичной дробью:Например, X= 3,4∙Е.
2)
Отрезок х1,
оказывается состоящим из n отрезков,
равных е1 и отрезка х2, который
короче отрезка е1,.
Тогда ,
где 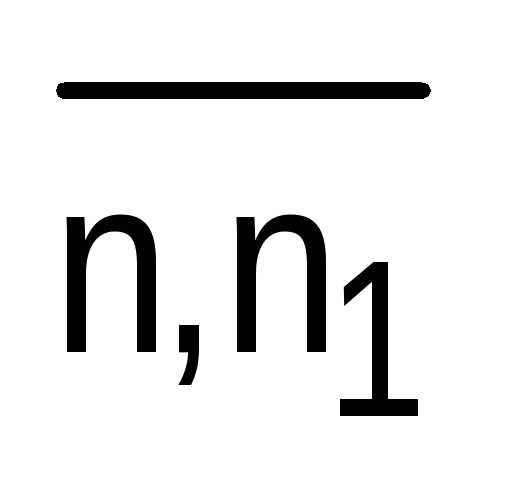 и
и 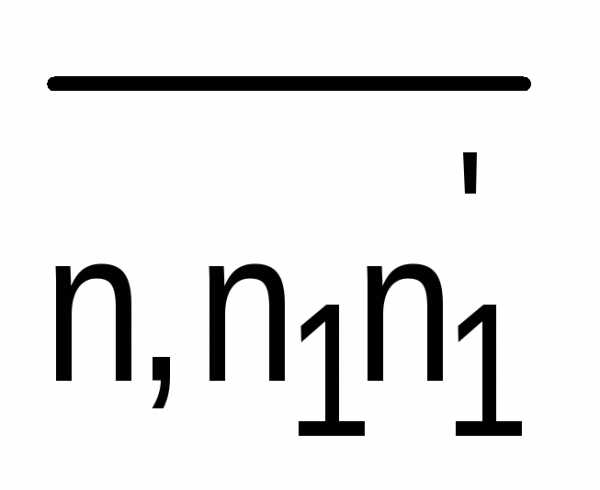 — приближенные значения длины отрезка х с
недостатком и с избытком с точностью
до 0,1.
— приближенные значения длины отрезка х с
недостатком и с избытком с точностью
до 0,1.
Ясно, что во втором случае процесс измерения длины отрезка х можно продолжать, взяв новый единичный отрезок е2 — сотую часть отрезка е.
На практике этот процесс измерения длины отрезка на каком-то этапе закончится. И тогда результатом измерения длины отрезка будет либо натуральное число, либо конечная десятичная дробь. Если же представить этот процесс измерения длины отрезка в идеале (как и делают в математике), то возможны два исхода:
1)
На k-том
шагу процесс измерения окончится. Тогда
длина отрезка х выразится
конечной десятичной дробью вида 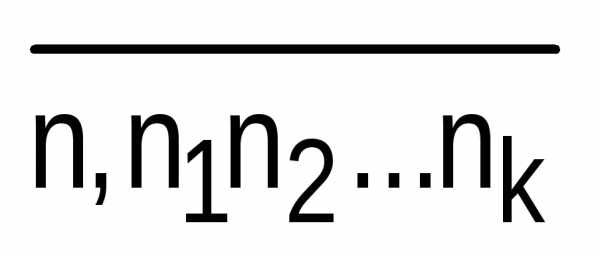 .
.
2)
Описанный процесс измерения длины
отрезка х продолжается
бесконечно. Тогда отчет о нем можно
представить символом 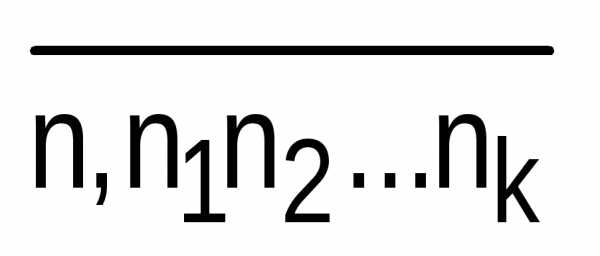 ,который
называют бесконечной
десятичной дробью.
,который
называют бесконечной
десятичной дробью.
Как
убедиться в возможности второго исхода?
Для этого достаточно произвести
измерение длины такого отрезка, для
которого известно, что его длина выражена,
например, рациональным числом 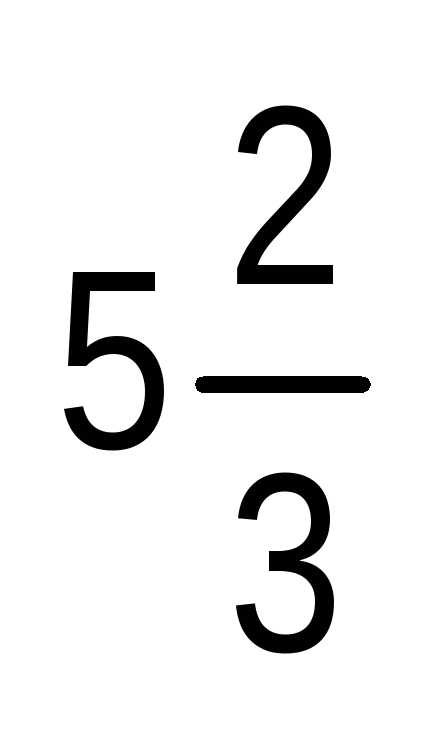 .
Если бы оказалось, что в результате
измерения длины такого отрезка получается
конечная десятичная дробь, то это
означало бы, что число
.
Если бы оказалось, что в результате
измерения длины такого отрезка получается
конечная десятичная дробь, то это
означало бы, что число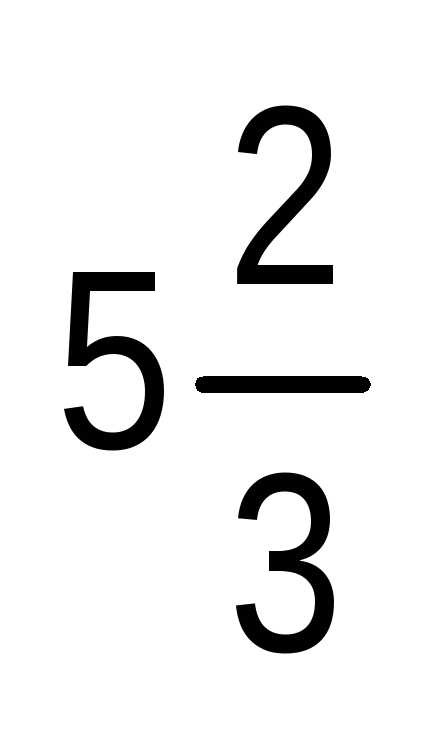 можно представить в виде конечной
десятичной дроби, что невозможно:
можно представить в виде конечной
десятичной дроби, что невозможно: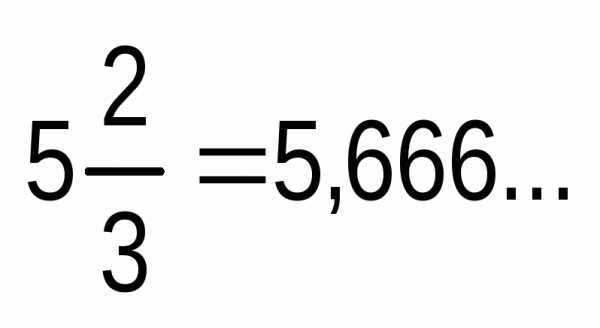 .
.
Итак, при измерении длин отрезков могут получаться бесконечные десятичные дроби. Но всегда ли эти дроби периодические? Ответ на этот вопрос отрицателен: существуют отрезки, длины которых нельзя выразить бесконечной периодической дробью (т.е. положительным рациональным числом) при выбранной единице длины. Это было важнейшим открытием в математике, из которого следовало, что рациональных чисел недостаточно для измерения длин отрезков.
Теорема. Если единицей длины является длина стороны квадрата, то длина диагонали этого квадрата не может быть выражена положительным рациональным числом.
Доказательство. Пусть длина стороны квадрата выражается
числом 1. Предположим противное тому,
что надо доказать, т.е., что длина диагонали АС квадрата ABCD выражается
несократимой дробью 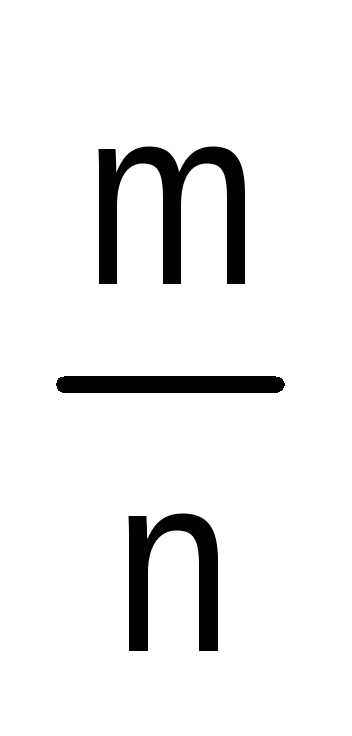 .
Тогда по теореме Пифагора, выполнялось
бы равенство и
.
Тогда по теореме Пифагора, выполнялось
бы равенство и 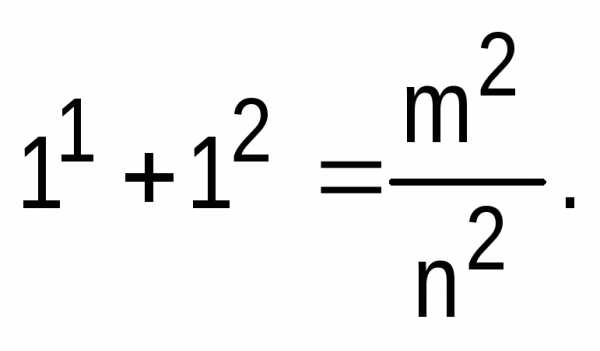 Из него следует, что m2 = 2n2.
Значит,
m2—четное
число, тогда и число m — четно
(квадрат нечетного числа не может быть
четным). Итак, m=2р. Заменив
в равенстве m2 =
2n2 число m на 2р, получаем,
что 4р2 = 2n2,
т.е. 2p2 = n2.
Отсюда следует, что n2 четно, следовательно, n
— четное число. Таким образом, числа m
и n четны,
значит, дробь
Из него следует, что m2 = 2n2.
Значит,
m2—четное
число, тогда и число m — четно
(квадрат нечетного числа не может быть
четным). Итак, m=2р. Заменив
в равенстве m2 =
2n2 число m на 2р, получаем,
что 4р2 = 2n2,
т.е. 2p2 = n2.
Отсюда следует, что n2 четно, следовательно, n
— четное число. Таким образом, числа m
и n четны,
значит, дробь 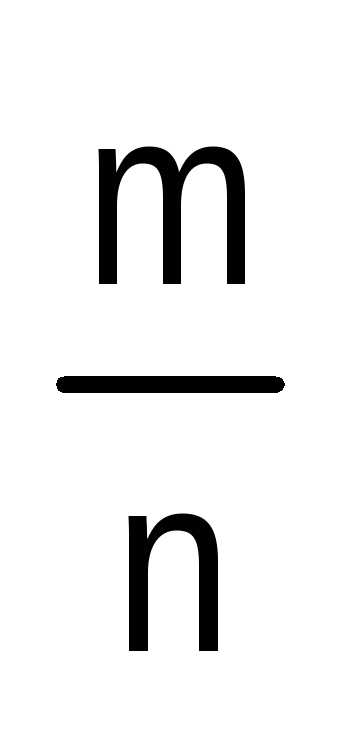 можно
сократить на 2, что противоречит
предположению о ее несократимости.
Установленное противоречие доказывает,
что если единицей длины является длина
стороны квадрата, то длину диагонали
этого квадрата нельзя выразить
рациональным числом.
можно
сократить на 2, что противоречит
предположению о ее несократимости.
Установленное противоречие доказывает,
что если единицей длины является длина
стороны квадрата, то длину диагонали
этого квадрата нельзя выразить
рациональным числом.
Из доказанной теоремы следует, что существуют отрезки, длины которых нельзя выразить положительным числом (при выбранной единице длины), или, другими словами, записать в виде бесконечной периодической дроби. И значит, получаемые при измерении длин отрезков бесконечные десятичные дроби могут быть непериодическими.
Считают, что бесконечные непериодические десятичные дроби являются записью новых чисел — положительных иррациональных чисел. Так как часто понятия числа и его записи отождествляют, то говорят, что бесконечные непериодические десятичные дроби — это и есть положительные иррациональные числа.
Мы
пришли к понятию положительного
иррационального числа через процесс
измерения длин отрезков. Но иррациональные
числа можно получить и при извлечении
корней из некоторых рациональных чисел.
Так, 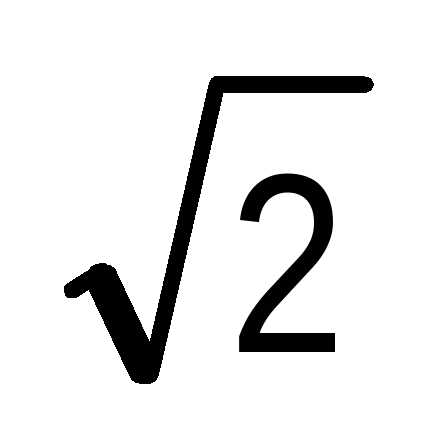 ,
, ,
, — это иррациональное числа. Иррациональными
являются такжеlg
5, sin
31, числа
— это иррациональное числа. Иррациональными
являются такжеlg
5, sin
31, числа  = 3,14…,е
= 2,7828…
и другие.
= 3,14…,е
= 2,7828…
и другие.
Множество положительных иррациональных чисел обозначают символомJ+.
Объединение двух множеств чисел: положительных рациональных и положительных иррациональных называют множеством положительных действительных чисел и обозначают символом R+. Таким образом, Q+J+= R+. При помощи кругов Эйлера эти множества изображены на рисунке 3.
Любое положительное действительное число может быть представлено бесконечной десятичной дробью — периодической (если оно является рациональным), либо непериодической (если оно является иррациональным).
Действия над положительными действительными числами сводятся к действиям над положительными рациональными числами.
Сложение и умножение положительных действительных чисел обладает свойствами коммутативности и ассоциативности, а умножения дистрибутивно относительно сложения и вычитания.
С помощью положительных действительных чисел можно выразить результат измерения любой скалярной величины: длины, площади, массы и т.д. Но на практике часто нужно выразить числом не результат измерения величины, а ее изменение. Причем ее изменение может происходить различно — она может увеличиваться, уменьшаться или оставаться неизменной. Поэтому, чтобы выразить изменение величины, кроме положительных действительных чисел нужны иные числа, а для этого необходимо расширить множество R+, присоединив к нему число 0 (нуль) и отрицательные числа.
Объединение множества положительных действительных чисел с множеством отрицательных действительных чисел и нулем есть множество R всех действительных чисел.
Сравнение действительных чисел и действия над ними выполняются по правилам, известным нам из школьного курса математики.
studfiles.net
Лекция 7. Действительные числа
Лекция 7. Действительные числа
7.1.Действительные числа. Расширенная числовая прямая. Окрестности
7.2.Модуль вещественного числа
7.3.Ограниченные и неограниченные множества. Конечные и бесконечные множества
7.4.Натуральные числа
7.5.Аксиома индукции и следствие из нее. Метод математической индукции
7.6.Принцип Архимеда. Усиленный принцип Архимеда
7.7. Лемма Бореля о покрытии
7.8. Теорема о вложенных промежутках
7.9. Открытые и замкнутые множества
Литература
А.В.Дорофеева «Высшая математика» Глава IV, § 4.1 – 4.4 стр.71-82
Дополнительно
Р.Курант, Г.Роббинс «Что такое математика?» Глава I «Натуральные числа» стр. 25-44, дополнение к главе I «Теория чисел» стр.45-76, глава II Математическая числовая система стр. 77-98
Контрольные задания
1.Как определяются элементы множества действительных чисел?
2.Дайте различные варианты определения модуля вещественного числа
3.Дайте определение инфинума (нижней грани) числового множества
4.Докажите, что ограниченное снизу числовое множество имеет нижнюю грань.
5.Как строится множество натуральных чисел?
6Докажите, что множество натуральных чисел не ограничено сверху
7.Методом математической индукции докажите
8.Сформулируйте определение ограниченного снизу множества и нижней границы, приведите примеры
9.Сформулируйте и докажите теорему Принцип Архимеда
10.Сформулируйте и докажите теорему Усиленный принцип Архимеда (включая доказательство второго случая для x<0).
Определение 7.1.
Множество элементов, обладающих свойствами I-V, содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент — действительным числом.
Это определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет условиям I-V.
Геометрически множество действительных чисел изображается направленной (ориентированной) прямой, а отдельные числа — точками этой прямой (см.рис. 7.1.(2))
Рис. 7.1. (2)
Поэтому совокупность действительных чисел часто называют числовой прямой или числовой осью, а отдельные числа — ее точками. В связи с этим иногда вместо а < b (соответственно вместо b > а) говорят, что точка а лежит левее точки b (точка b лежит правее точки а).
Часто бывает удобно дополнить множество действительных чисел элементами, обозначаемыми через +∞ и — ∞ и называемыми соответственно плюс бесконечностью и минус бесконечностью, считая при этом по определению, что для любого числа х R. выполняется неравенство -∞< х < +∞.
Множество действительных чисел R, дополненное элементами +∞ и —∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается
Иногда бывает удобно дополнить множество действительных чисел R одним элементом ∞ (бесконечностью без знака), в этом случае бесконечность ∞ уже не связана соотношением порядка с действительными числами. Бесконечности +∞, ∞и ∞ называются также бесконечно удаленными точками числовой прямой, в отличие от ее остальных точек, которые называются конечными точками числовой прямой.
Сформулируем определения некоторых важных типов подмножеств расширенной числовой прямой R. Пусть a , b , а ≤b. Множество
[а, b] = {х: х , а ≤x≤b}
называется отрезком, множество
(a,b) = {х: х , а < х < b}
— интервалом, множества
[а, b) = {х: х , а ≤ х < b},
(а,b] = {х: х , а < х ≤b}
— полуинтервалами, а все они — промежутками расширенной числовой оси. Точки а и b называются концами этих промежутков, а точки х такие, что а < х < b, — их внутренними точками. Если а и b — числа, а ≤b, то число b — а называется длиной соответствующего промежутка, а сам промежуток называется конечным.
Определение 7.1(2).
U(a, ε) = (a — ε, a + ε ) (см рис.7.1(3)
Рис. 7.1(3).
Модуль вещественного числа
Определение 7.2.
Модулем действительного числа х называется такое неотрицательное число, обозначающееся |x|, такое, что:
Например, |6|=6, 6≥0, |-7| = -(-7)=+7, -7<0
Если расположить действительные числа на числовой оси, то модуль |x| любого числа х представляет собой расстояние от начала отсчета 0 до соответствующей точки А с абсциссой х: |x|=OA (см.рис. 4.2(1))
Рис.7.2(1).
Наконец, модуль вещественного числа х можно определить следующим образом:
|x| = max {x, -x}.
где max{a,b} – наибольшее из чисел a и b
Например, |2| = max {2, -2}=2,
|-9| = max {-9, -(-9))} = max{-9, 9} = 9.
Если модуль числа х удовлетворяет неравенству
(см. рис.7.2(2))
Рис.4.2.(2)
Замечание 7.2(1).
Замечание 7.2(2).
Таким же образом определяется функция модуль y=F(x)=|x|
То есть в части x≥0 график функции совпадает с графиком y=x, а при x<0 с y=-x, то есть график y=x в этой части отражается относительно оси x
Натуральные числа
Определение 4.4.
Числа вида
2 = 1+1
3 = 2+1
и т.д.
называются натуральными и их множество обозначается N
Множество натуральных чисел обладает следующим характеристическим свойством:
Если:
Теорема 7.4.
Множество натуральных чисел неограниченно сверху
Доказательство
Докажите методом от противного, используя определение верхней грани
Аксиома индукции
Пусть Е – некоторое непустое подмножество множеств натуральных чисел. Тогда в множестве Е есть наименьший элемент.
Замечание 7.5.
Может произойти так, что в последовательности Р(1), Р(2),…P(k),… первым истинным является не первое, а некоторое j-е. Тогда принцип индукции можно сформулировать следующим образом:
1)P(j) истинно (база индукции)
2)Для произвольного k≥j, если P(k) истинно, то истинно P(k+1)
Тогда P(n) истинно для всех n ≥j
То есть не обязательно начинать рассмотрение с к=1 (хотя чаще всего начинают как раз с к=0 или 1).
Пример 7.5.
Используя принцип индукции для целых чисел, нужно доказать, что для любого целого числа n ≥ 4 имеет место неравенство n! > 2n.
При использовании индукции по n, в данном случае нельзя начинать с n = 1, поскольку утверждение для n=1 неверно. Начальной точкой должно быть n = 4, т.к. утверждение неверно также для n = 2 и n = 3.
Таким образом, база индукции рассматривается для первого утверждения, соответствующего n=4
Р(n) — утверждение «n! > 2n«.
Сначала докажем утверждение для n = 4. При n = 4 имеем 4! = 24 и
24 = 16, так что 4! > 24.
Индукционный переход:
По индуктивному предположению имеем k!> 2k. Нам нужно доказать, что (k+1)> 2k+1 метим, что желаемый результат можно получить, если умножить левую часть неравенства на (k+ 1), а правую — на 2. Поэтому, если мы покажем, что (k+1)>2, то получим k!> 2k и (k+1) > 2 и сможем сделать вывод, что (k+1)!> 2k+1. Поскольку k ≥ 4, то k > 2. Следовательно, (k+1)k! > 2 · 2k и (k+1)!> 2k+1. Таким образом, n! > 2n для каждого n > 4.
Принцип Архимеда
Теорема 7.6(1)
Каково бы ни было действительное число а, существует такое натуральное число n, что
n > а.
Доказательство
Если бы утверждение теоремы не имело места, то нашлось бы такое число а, что для всех натуральных чисел n выполнялось бы неравенство n≤а, т. е. множество натуральных чисел N было бы ограничено сверху. Тогда существовала бы конечная верхняя грань:
Поскольку β — 1 < β, то в силу определения верхней грани (найдется такое натуральное число n, что n > β — 1, т. е. n + 1 > β, но n + 1 — также натуральное число: /, поэтому данное неравенство противоречит условию существования верхней грани.
Замечание 7.6
Пусть а=1, тогда для любого действительного х существует единственное целое n такое, что n≤ x< n+1.
n=[x] называется целой частью вещественного числа х (см график соответствующей функции на рис. 7.6(1)
{x} = х – [x] называется дробной частью вещественного числа х (график см. на рис.7.6(2))

Рис.7.6(1) Рис. 7.6(2)




Лекция 7. Действительные числа
7.1.Действительные числа. Расширенная числовая прямая. Окрестности
7.2.Модуль вещественного числа
7.3.Ограниченные и неограниченные множества. Конечные и бесконечные множества
7.4.Натуральные числа
7.5.Аксиома индукции и следствие из нее. Метод математической индукции
7.6.Принцип Архимеда. Усиленный принцип Архимеда
7.7. Лемма Бореля о покрытии
7.8. Теорема о вложенных промежутках
7.9. Открытые и замкнутые множества
Литература
А.В.Дорофеева «Высшая математика» Глава IV, § 4.1 – 4.4 стр.71-82
Дополнительно
Р.Курант, Г.Роббинс «Что такое математика?» Глава I «Натуральные числа» стр. 25-44, дополнение к главе I «Теория чисел» стр.45-76, глава II Математическая числовая система стр. 77-98
Контрольные задания
1.Как определяются элементы множества действительных чисел?
2.Дайте различные варианты определения модуля вещественного числа
3.Дайте определение инфинума (нижней грани) числового множества
4.Докажите, что ограниченное снизу числовое множество имеет нижнюю грань.
5.Как строится множество натуральных чисел?
6Докажите, что множество натуральных чисел не ограничено сверху
7.Методом математической индукции докажите
8.Сформулируйте определение ограниченного снизу множества и нижней границы, приведите примеры
9.Сформулируйте и докажите теорему Принцип Архимеда
10.Сформулируйте и докажите теорему Усиленный принцип Архимеда (включая доказательство второго случая для x<0).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
