Примеры чисел натуральные числа – Натуральные числа. Ряд натуральных чисел. Математика 5 класс

Содержание

Натуральные числа. Ряд натуральных чисел. Математика 5 класс

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.

Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

Наименьшее натуральное число – единица.
У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
Натуральный ряд не имеет наибольшего числа, он бесконечен.

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.

tutomath.ru

Натуральные числа

История

Натуральные числа и различные системы для их обозначения использовались еще в древних цивилизациях: Древнем Междуречье, Древнем Египте, Древнем Китае, в племенах Майя. Понятие числа «ноль», по видимому, появилось позже понятия натуральных чисел в позднем Вавилоне и у Майя.

Замечание 1

В самые древние времена для счета использовали палочки. Такой способ записи сохранился в римском исчислении. Число при такой записи представляло собой сумму или разность палочек, которая была записана без каких-либо знаков.

С развитием систем счисления определенные числа стали обозначать буквами алфавита. В современных системах счисления значение каждой цифры числа определяет ее место в записи числа. Первой такой системой счисления была вавилонская (шестидесятеричная) и индийская (десятичная).

Вариантом индийской десятичной системой счисления является современная арабская система с тем различием, что в индийской системе отсутствовал ноль. Цифру $0$ придумали арабы, после чего система счисления приняла современный вид.

Для счисления времени используется шестидесятеричная система (за основу взято число $60$): $1$ час содержит $60$ минут, $1$ минута — $60$ секунд.

В работах математика Пьера де Ферма были положены основы теории чисел или высшей арифметики как отдельной науки, которая изучает чистые, формальные свойства натуральных чисел.

Натуральные числа. Множество натуральных чисел

Натуральные числа $1, 2, 3, \dots$ используются для счёта (одна груша, две груши, три груши и т.д.) или для указания порядкового номера предмета среди ему подобных.

Натуральные числа принято записывать с помощью арабских цифр: $0, 1, 2, 3, 4, 5, 6, 7, 8, 9$.

Рисунок 1.

Определение 1

Натуральные числа (или естественные числа) — числа, которые возникают естественным образом при подсчете чего-либо.

Пример 1

Натуральными будут числа: $3, 48, 157, 1089, 25556$.

Если выстроить все натуральные числа в порядке их возрастания, то получим

натуральный ряд.

Для определения натуральных чисел существует два подхода:

Числа, которые возникают при подсчете (нумерации) предметов (например, первый, второй и т.д.).
Числа, которые используют для обозначения количества предметов (нет стула, один стул, два стула и т.д.).

При первом подходе натуральный ряд начинается с единицы, при втором — с нуля.

Математики не пришли к единому выводу считать ли ноль натуральным числом. В большинстве российских источников традиционным является первый подход. Второй подход широко используется в программировании (например, при индексации массивов, нумерации битов машинного кода и т.д.).

Замечание 2

К натуральным числам не относятся ни отрицательные, ни нецелые числа.

Определение 2

Множество всех натуральных чисел обозначается $N=\left\{1,\ 2,\ 3,\ 4,\ \dots ,\ n,\ \dots \right\}$ и характеризуется своей бесконечностью, т.к. для любого натурального числа $n$ существует натуральное число, которое будет большее $n$.

Пример 2

Какие из чисел являются натуральными?

\[-6;\ \ 5;\ \ 0,6;\ \ \ \frac{1}{2};\ \ \ \sqrt[3]{5};\ \ 38;\ \ \ -38;\ \ 12,5;\ \ 4.\]

Ответ: $5;\ \ 38;\ \ \ 4.$

При формулировке и доказательстве многих теорем арифметики натуральных чисел удобно использовать и ноль, поэтому при первом подходе применяется понятие расширенного множества натуральных чисел, которое содержит ноль и обозначается $N_0$ или $Z_0$.

Ноль как натуральное число

В русской литературе принято исключать нуль из числа натуральных чисел ($0\notin N$), а множество натуральных чисел с нулём обозначают $N_0$.

В международной математической литературе множество $\left\{1,\ \ 2,\ \ 3,\ \dots \right\}$ принято называть множеством положительных целых чисел и обозначать $Z+$. Множество $\left\{0,\ \ 1,\ \ 2,\ \dots \right\}$ принято называть

множеством неотрицательных целых чисел и обозначать $Z{\ge 0}$.

Чтобы прочитать натуральное число, нужно выполнить следующие действия:

Разбить число справа налево на группы из $3$ цифр.
Прочитать слева направо по очереди группы из $3$ цифр и добавить название класса.
Название класса пропускают, если в группе цифр все нули.

Рисунок 2.

Каждую цифру класса называют разрядом класса.

Меньшим натуральным числом является то, которое при проведении подсчета используется раньше. Например, число $9$ меньше $20$ (записывается $9 55$.

Аксиомы Пеано для натуральных чисел

Множество $N$ будем называть множеством натуральных чисел, если зафиксирован некоторый элемент единица $1\in N$ и функция следования $S:N\to N$ так, что выполнены следующие условия:

$1\in N$: единица является натуральным числом.
Если $x\in N$, то $S\left(x\right)\in N$: Если число — натуральное, то следующее число за ним тоже натуральное}.
$\nexists x\in N\ \left(S\left(x\right)=1\right)$: Не существует натурального числа, которое находится перед единицей}.
Если $S\left(b\right)=a$ и $S\left(c\right)=a$, тогда $b=c$: Если натуральное число $a$ следует за числом $b$ и за числом $c$, то $b=c$.
Аксиома индукции. Пусть $P\left(n\right)$ — некоторый одноместный предикат, который зависит от натурального числа $n$. Тогда:

Если $P\left(1\right)$ и $\forall n\left(P\left(n\right)\Longrightarrow P\left(S\left(n\right)\right)\right)$, то $\forall n\ P\left(n\right)$:

Если некоторое высказывание $P$ верно для $n=1$ и для любого $n$ из истинности $P\left(n\right)$ следует истинность $P\left(n+1\right)$, то $P\left(n\right)$ верно для любого натурального $n$.

Все аксиомы отражают представление о натуральном ряде и числовой линии.

Теоретико-множественное определение натуральных чисел (определение Фреге—Рассела)

По теории множеств единственным объектом конструирования любых математических систем является множество.

Таким образом, исходя из понятия множества натуральные числа вводятся по двум правилам:

$0=\emptyset $
$S\left(n\right)=n\cup \left\{n\right\}$
Заданные таким образом числа называются порядковыми или ординальными.

Описываются первые порядковые числа и натуральные числа, которые им соответствуют, следующим образом:

$0=\emptyset $
$1=\left\{0\right\}=\left\{\emptyset \right\}$
$2=\left\{0,\ \ 1\right\}=\left\{\emptyset ,\ \ \left\{\emptyset \right\}\right\}$
$3=\left\{0,\ \ 1,\ \ 2\right\}=\left\{\emptyset ,\ \ \left\{\emptyset \right\},\ \ \left\{\emptyset ,\ \ \left\{\emptyset \right\}\right\}\right\}$

spravochnick.ru

Натуральные числа — основы, двузначные числа, однозначные числа

Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.

Yandex.RTB R-A-339285-1

Общее представление о натуральных числах

На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.

Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.

Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.

Десятичная запись натурального числа

Вспомним, как изображаются следующие знаки (укажем их через запятую): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Указанные знаки мы называем цифрами.

Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.

Укажем примеры правильной записи натуральных чисел: 703, 881, 13, 333, 1 023, 7, 500 001. Отступы между цифрами не всегда одинаковы, об этом подробнее будет сказано ниже при изучении классов чисел. Заданные примеры показывают, что при записи натурального числа не обязательно должны присутствовать все цифры из указанного выше ряда. Некоторые из них или все могут повторяться.

Определение 1

Записи вида: 065, 0, 003, 0791 не являются записями натуральных чисел, т.к. слева располагается цифра 0.

Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.

Количественный смысл натуральных чисел

Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.

Приступим к натуральным числам, записи которых совпадают с записями цифр, т.е.: 1, 2, 3, 4, 5, 6, 7, 8,

zaochnik.com

Материал по математике «Числа. Натуральные числа»

Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т. е. для вычисления их количества и порядка.

Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.

Натуральные числа — это числа, начиная с единицы. Они образуются естественным образом при счёте.

Например, 1, 2, 3, 4, 5… – первые натуральные числа.

Наименьшее натуральное число — один. Наибольшего натурального числа не существует. При счёте число ноль не используют, поэтому ноль натуральное число.

Натуральный ряд чисел — это последовательность всех натуральных чисел. Запись натуральных чисел:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…

В натуральном ряду каждое число больше предыдущего на единицу.

Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.

Система счёта (счисления) , которую мы используем, называется десятичной позиционной.

Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т. е. от разряда, где она записана.

Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.

Всякое натуральное число легко записать в виде разрядных слагаемых.

Числа 1, 10, 100, 1000… – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:

307 898 = 300 000 + 7 000 + 800 + 90 + 8

Самые употребляемые числа имеют не больше 12 разрядов. Числа, которые имеют больше 12 разрядов,относятся к группе больших чисел.

Когда запись натурального числа состоит из одного знака — одной цифры, его называют однозначным числом.

числа 1, 5, 8 — однозначные числа.

Если запись числа состоит из 2-х знаков — двух цифр, его называют двузначным числом.

числа 14, 33, 28, 95 — двузначные числа,

числа 386, 555, 951 — трехзначные числа,

числа 1346, 5787, 9999 — четырехзначные числа и т. д.

Обозначение натуральных чисел:

Множество натуральных чисел обозначают символом N.

Таблица натуральных (простых) чисел до 10 000.

Классы натуральных чисел.

Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Для чтения натуральных чисел их разбивают, начиная справа, на группы по 3 цифры в каждой. 3 первые цифры справа – это класс единиц, 3 следующие – это класс тысяч, далее классы миллионов, миллиардов и так далее. Каждая из цифр класса называется его разрядом.

Сравнение натуральных чисел.

Из 2-х натуральных чисел меньше то число, которое при счете называется ранее. Например, число 7 меньше 11 (записывают так: 7 < 11). Когда одно число больше второго, это записывают так: 386 > 99.

Весь материал — в документе.

videouroki.net

Натуральные числа — Циклопедия

Kampus.kz: Математика. Урок 1 — Числа: Натуральные числа

Математика. Натуральные числа: Натуральные числа. Центр онлайн-обучения «Фоксфорд» [4:55]

Натуральные числа — это ряд 1, 2, 3, 4, 5… — чисел, каждое из которых выражает счетное количество предметов: мощность конечного множества элементов, означающих те предметы. Указывают количество и порядок следования перенумерованных объектов (каждое натуральное число имеет «свое» место — уникальный номер).

В полной совокупности натуральные числа суть математический объект: это бесконечное множество, вполне упорядоченное, с минимальным элементом (нуль или единица), со сложением и умножением.

Понятие и соответствующая теоретическая концепция прослеживается с глубокой древности человечества. Познание натуральных чисел на элементарном уровне называется арифметикой, а на более глубоком уровне — является частью теории чисел («высшей арифметики»). Натуральные числа стали основой для развития ряда дисциплин классической математики.

В математической традиции с XIX века натуральные числа определяются через аксиомы и зачастую включают 0 (нуль или ноль,) — мощность пустого множества, «количество» «ни одного предмета» (в российской математической литературе 0 обычно не считается натуральным числом). Распространенное обозначение множества натуральных чисел — [math]\mathbb{N}[/math].

[править] Формальное определение

Индуктивное (рекурсивное) определение: Натуральные числа, не считая ноля, — это единица или её сумма с любым другим натуральным числом.

Натуральные числа могут быть описаны аксиоматически. Одна из возможных систем — аксиомы арифметики Пеано:

Единица есть натуральное число: [math]1\in \mathbb{N}[/math];
Число, следующее за натуральным, также является натуральным числом: [math]n \in \mathbb{N} \implies n+1 \in \mathbb{N}[/math];
Единица не следует ни за каким натуральным числом: [math]\nexists n : n+1=1[/math]
Если натуральное число a следует за натуральным числом b и a следует за натуральным числом с, то b = c: [math](a=b+1) \land (a=c+1) \implies b=c[/math];
Аксиома математической индукции: Если утверждение (зависящее от параметра) доказано для числа 1 (база индукции) и если из допущения, что оно верно для натурального числа n, следует, что оно верно для следующего за n натурального числа (индукционное предположение), то это утверждение верно для всех натуральных чисел.

Последняя аксиома позволяет доказывать утверждения сразу обо всей бесконечной последовательности натуральных чисел с помощью метода математической индукции.

[править] Система обозначения

Существуют различные методы обозначения натуральных чисел, обычно называемые системами счисления. С дополнением метки-заполнителя — структурного ноля — натуральные числа можно записать в произвольной позиционной системе счисления, например, — в двоичной (обычно применяемой в компьютерах): 1, 10, 11, 100, 101… — или в распространенной в настоящее время в литературе и в быту десятичной: десятью арабскими цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно записать любое число: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … 99, 100, 101, 102 … В языке выражаются через числительные.

Всякая из этих систем — способ производства уникального номера для любого из бесконечного множества чисел. Из формы этого названия можно обычно без справочных материалов получить идентичность натурального числа, его место в ряду натуральных и другие свойства (например, делимость.)

Ряд древних цивилизаций: Древнее Междуречье, Древний Египет, Древний Китай, Майя знали натуральные числа и имели различные знаковые системы для указания (фиксации, означения). Концепция числа ноль, по видимому, появилась позже, чем понятие натуральных чисел: явное употребление структурного нуля известно у культур Вавилон и Майя.

Как отдельная наука, изучающая чистые, формальные свойства натуральных чисел, Теория чисел, или высшая арифметика, основополагается в работах математика-любителя Пьера де Ферма.

Натуральные числа целиком охвачены арифметикой, так как можно:

их складывать и перемножать любым образом,
вычитать меньшее число из большего,
делить число на любой из образующих его множителей.

По сложению натуральные числа образуют коммутативную полугруппу: любые два натуральных числа можно сложить, и сложение коммутативно и ассоциативно:

[math]a+b=b+a[/math] (коммутативность или перестановочное свойство: от перемены мест слагаемых сумма не меняется)

[math](a + b) + c=a + (b + c)[/math] (ассоциативность)

Умножение натуральных чисел также коммутативно и ассоциативно:

[math]a \cdot b = b \cdot a[/math]

[math](a \cdot b) \cdot c=a \cdot (b \cdot c)[/math]

Умножение дистрибутивно по сложению:

[math]a\cdot(b+c) = a \cdot b + a \cdot c[/math]

Натуральные числа — множество вполне упорядоченное: в любом подмножестве будет минимальный элемент. Это словно «отражение» правила индукции, принцип метода бесконечного спуска.

Если из большего числа «отсчитать обратно по единице», «вычесть», меньшее, то получится другое меньшее, а [math]a-b=b, a \gt b \iff a=2b[/math]. Уже́ у целых чисел такое определение нарушается ровно в «другой половине случаев», когда вычитается отрицательное, выдавая число, большее первого.

Каждое натуральное число >1 обладает единственным с точностью до порядка сомножителей разложением (факторизацией) на простые множители. Это Основная теорема арифметики.

[править] Расширение до целых чисел и дальше

Если к натуральным числам добавить ноль и отрицательные числа (обратные натуральным по сложению), то в совокупности получится расширение понятия числа до кольца целых чисел [math]\mathbb{Z}[/math], которое наиболее четко являет основу теории чисел. Отрицательные числа можно мыслить, как получаемые от обратного счёта — последовательного убавления по единице — которое вводит ряд отрицательных чисел. Из тех каждое сложением обнуляет противоположное ему натуральное: [math]n+(-n)=0[/math].

Если рассматривать отношения целых чисел — дроби — то получится поле рациональных чисел [math]\mathbb{Q}[/math]. Пополнение этого поля по стандартной метрике (расстояние между числами равно модулю их разности) будет представлять собой поле действительных чисел [math]\mathbb{R}[/math], представимое как допустимо бесконечные и апериодичные цепные дроби. Алгебраическое замыкание поля действительных чисел образует поле комплексных чисел [math]\mathbb{C}[/math] (его можно представлять как поле действительных чисел, к которому добавлена мнимая единица [math]i[/math]: [math]i^2=-1[/math].

Бухштаб А. А. Теория чисел — М.: «Просвещение», 1966.
К. Айерленд, М. Роузен, Классическое введение в современную теорию чисел — М., 1987.

cyclowiki.org

Что такое натуральное число в математике

Все дети с ранних лет изучают математику. Поначалу она позволяет узнать простые вещи, легко применимые в жизни, но с течением времени задачи постоянно усложняются. Появляется и новая терминология, по которой не всегда можно понять, что имеется в виду. Например, что такое натуральное число в математике?

В древние времена люди не пользовались цифрами так, как делают это сейчас, однако счет всё равно был им необходим. Предметы сравнивались по количеству с чем-то, например, кто-то имел столько же ягод, сколько и пальцев на одной руке. Постепенно люди изобрели систему счета, а с ней появились и новые термины.

Что такое натуральное число в математике?

Это понятие относится к одним из самых старых, так как оно родилось из-за древней необходимости научиться считать количество обычных предметов. Что значит натуральное число? Чаще всего дается следующее определение – это числа, которые возникают при подсчете, причем происходит подобное естественным образом.

Отсюда берется и второе название этого термина – естественные числа. Своей последовательностью, расположенностью по возрастанию, они образуют натуральный ряд. Иначе говоря, все цифры, начиная с единицы, которые используются для подсчета предметов, являются натуральными.

Таким образом, существует самое малое натуральное число – им является единица. Наибольшего же не бывает, так как к любой цифре можно добавить ещё один. Ноль не входит в натуральный ряд, так как с его помощью нельзя ничего посчитать, хотя далеко не все ученые с этим согласны.

Определение натуральных чисел

Подобные цифры определяются двумя главными методами. Первый из них подразумевает перечисление всего имеющегося, а второй называет итоговое количество.

Первый метод определения является подсчетом или нумерацией имеющихся предметов. Например, видя перед собой несколько яблок, человек может посчитать их – одно, два, три…
Второй метод определения называет итоговое количество имеющихся предметов. Таким образом, если яблок нет совсем, то можно сказать, что предметов нет. Это значит, что при подсчете появляется ноль.

В этой цифре и заключается основная разница между двумя данными методами определения. В первом случае минимальным числом является единица, а во втором возможно и использование нуля. Математики так и не смогли прийти к единогласному решению о том, какой метод лучше, и стоит ли ставить ноль в один ряд с другими натуральными числами.

Как правило, применяется всё же первый вариант, оставляющий спорную цифру в стороне. Тем не менее, в некоторых трудах, вроде Бурбаки, используется другой подход. Помимо этого, ноль является неотъемлемой и широко применяемой частью в мире программирования.

Особенности натуральных чисел

Главное, о чем нужно помнить при упоминании подобных чисел, так это об их обязанности быть естественными. Они должны быть такими, чтобы с их помощью было возможно подсчитать количество каких-то предметов. Естественные числа должны быть доступными и понятными для всех.

По этой причине к ним не относятся отрицательные показатели и различные нецелые числа. Например, рациональное, обозначающееся в виде дроби, или вещественные, представляющее собой математический объект, не смогут стать частью натурального ряда.

Что такое натуральное число в математике? Все эти цифры принято обозначать буквой N. Её выбрали потому, что на латинском языке слово естественный пишется как naturalis, то есть начинается с литеры N. Число, подразумеваемое под этим обозначением, бесконечно.

Нередко для доказательства сложных теорем полезно помнить и о нуле. Он входит в расширенный натуральный ряд, который обозначают с помощью соответствующей цифры, приписанной снизу к букве N. Иногда вместо неё применяете Z, вновь с тем же маленьким нулем рядом.

Операции с натуральными числами

В математике существует понятие замыкания. Оно обозначает минимально возможное расширение какого-то множества, операции с которым не выходят за его пределы. В отношении натуральных чисел выделяется несколько таких замкнутых операций.

В первую очередь, это сложение. Естественные числа легко можно сложить друг с другом, чтобы получить какую-то сумму.
Возможно и умножение. Два натуральных множителя дадут произведение.
Наконец, используется возведение в степень. Оно состоит из основания и показателя. В том случае, если обе части представлены натуральными числами, то и результат получится таким же.

Иногда в данном вопросе рассматриваются ещё две операции. Их проблема заключается в том, что они применимы не для всех случаев. Иногда подобное может существовать, а иногда нет. К этим операциям относятся:

Вычитание. Оно даст натуральное число только в том случае, если первая цифра будет больше второй. Иначе возможно получение отрицательного числа, не относящегося к натуральным, или же нуля, который является спорным;
То же самое относится и к делению. В самых простых примерах все числа в итоге будут естественными, однако существует множество ситуаций, в результате которых получатся нецелые.

Как правило, наука сосредотачивается на первых двух операциях – сложении и вычитании. Интересно, что именно они способствуют созданию кольца целых чисел – это происходит через бинарные сложения и умножения.

Что стоит знать о натуральных числах?

Цифры, используемые для счета, не всегда были такими, как мы их знаем сегодня. Изначально применялось относительно схематическое изображение, постепенно сформировавшееся в римские цифры.

Современный же вариант зародился в Индии, примерно полторы тысячи лет назад. Впоследствии они были привезены в европейские страны арабами, за что и получили своё известное название – арабские цифры. Несмотря на то, что натуральных чисел может быть любое количество, цифр всего десять – от нуля и до девятки.

Если рассматривать натуральный ряд, то в нем каждое число будет отличаться от предыдущего или последующего на единицу, при том, что сам ряд бесконечен. Однако, в процессе счета появляется так называемая десятичная позиционная.

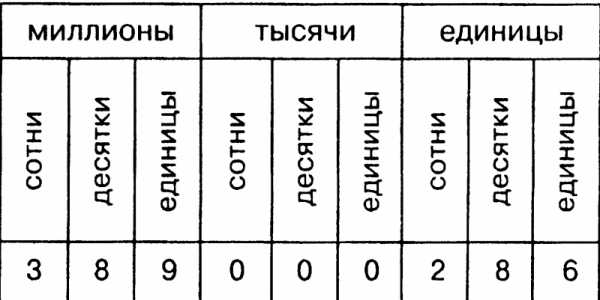
Под этим словом подразумевается тот факт, что когда числа доходят до десяти, они образуют новую единицу старшего разряда. Эти разряды бывают самыми разными – в частности, к ним относятся миллионы и миллиарды. В зависимости от их количества, разряды объединяют по классам.

Например, миллиарды могут исчисляться десятками или сотнями. Это будут разряды, но все они в целом образуют класс миллиардов. То же самое происходит и с разрядами миллионов, тысяч, сотен, десяток и единиц.

topkin.ru

Натуральные числа. Натуральный ряд. Однозначные числа | Учеба-Легко.РФ

Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Например: триста двадцать восемь — 328

пятьдесят тысяч четыреста двадцать один — 50421

Такую запись чисел называют десятичной. Последовательность всех натуральных чисел называют натуральным рядом:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

Самое маленькое натуральное число — единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего.

Натуральный ряд бесконечен, наибольшего числа в нем нет.

Значение цифры зависит от ее места в записи числа.

Например 375:

цифра 5 означает: 5 единиц, она на последнем месте в записи числа (в разряде единиц),

цифра 7 — десятки, она находится на предпоследнем месте (в разряде десятков),

цифра 3 — сотни, она стоит на третьем месте от конца (в разряде сотен) и т. д.

Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль».

Это число означает «ни одного». Помните! Нуль не относят к натуральным числам.

Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным.

Например, числа 1, 5, 8 — однозначные.

Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.

числа 14, 33, 28, 95 — двузначные,

числа 386, 555, 951 — трехзначные,

числа 1346, 5787, 9999 — четырехзначные и т. д.

uclg.ru