Алгебраические дроби. Сокращение алгебраических дробей
Тема: Разложение многочленов на множители
Урок: Алгебраические дроби. Сокращение алгебраических дробей
При делении числа на число мы получаем целое число :
Но при делении числа на число мы получаем уже не целое число, и это выражение называем арифметической дробью:
При делении некоторого одночлена на другой одночлен мы получаем третий одночлен:
Но при делении того же самого одночлена на другой одночлен мы не получаем одночлен, а получаем выражение, называемое алгебраической дробью:
Итак, при делении различных одночленов мы можем получить результат в двух видах: в виде одночлена или в виде алгебраической дроби, аналогично целым числам, когда в результате деления целого числа на целое число мы можем получить третье целое число либо арифметическую дробь.
Такая же ситуация возникает и при делении многочлена на одночлен.
в результате деления получен многочлен;
в результате деления получена алгебраическая дробь;
Обратим внимание, что целые числа, одночлены и многочлены также можно рассматривать как алгебраическую дробь в виде выражения деленного на единицу.
Алгебраическая дробь – это деление одного многочлена на другой многочлен: , P – числитель дроби, Q – знаменатель дроби; данные многочлены можно преобразовывать, раскладывать на множители любыми известными нам методами. Дробь можно сокращать на общие множители, то есть упрощать исходную дробь, так же как мы делали с арифметическими выражениями. Рассмотрим пример:
Пример 1:
Чтобы упростить данное выражение, нужно разложить числитель и знаменатель на простые множители:
Теперь можно сократить на общий множитель:
Итак, при работе с арифметическими дробями для упрощения выражения мы и числитель, и знаменатель разлагали на простые множители, опираясь на основную теорему арифметики о разложении составных чисел на простые множители, после чего сокращали общие множители.
По аналогии действия с алгебраическими дробями заключаются в следующем: нужно и числитель, и знаменатель разложить на множители, а после этого, если есть возможность общие множители сократить. Рассмотрим примеры:
Пример 2:
В результате деления одночленов получен новый одночлен;
Пример 3:
В результате деления одночленов получена алгебраическая дробь;
Пример 4:
Разложим числитель и знаменатель на множители:
В результате деления многочленов получена алгебраическая дробь;
Пример 5:
Раскладываем числитель и знаменатель на множители методом вынесения общего множителя:
Применим в знаменателе формулу разности кубов:
=
Сократим общий множитель:
В результате деления многочленов получена алгебраическая дробь;
Разложим числитель и знаменатель на множители:
Сократим общие множители:
В результате деления многочленов получена алгебраическая дробь;
Вывод: в данном уроке мы изучили новое понятие – алгебраическая дробь, и сравнили ее с уже известной нам арифметической дробью. Мы решили много различных примеров на сокращение алгебраических дробей.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет:
1. Вся элементарная математика (Источник).
2. Школьный помощник (Источник).
3. Интернет-портал Nado5.ru (Источник).
Рекомендованное домашнее задание:
Задание 1: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 435, ст.151;
Задание 2: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 436, ст.151;
Задание 3: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 445, ст.152;
interneturok.ru
Алгебраические дроби. Сокращение алгебраических дробей
Алгебраическая дробь – это дробь, числитель и знаменатель которой являются многочленами. Другими словами, алгебраическая дробь – это деление двух многочленов, записанное с помощью дробной черты.
Любую алгебраическую дробь можно представить в виде выражения:
где a и b – это многочлены и b≠0.
Дробная черта в записи алгебраической дроби заменяет собой скобки, которые должны были бы присутствовать, если частное было бы записано не в виде дроби:
| (a + 3) : (a2 + 9) = | a + 3 |
| a2 + 9 |
Примеры алгебраических дробей:
| a + 3 | ; | 7 | ; | 1 |
| a2 + 9 | x | 2 |
Обратите внимание на последний пример: обыкновенные дроби являются одновременно и алгебраическими, так как любое число можно считать многочленом, состоящим из одного члена.
Любой многочлен можно записать в виде алгебраической дроби, знаменатель которой равен единице:
| a2 + 9 = | a2 + 9 | ; 15 = | 15 | ; x2 + 2xy + y2 = | x2 + 2xy + y2 |
| 1 | 1 | 1 |
Сокращение алгебраических дробей
Основное свойство алгебраической дроби:
Если числитель и знаменатель алгебраической дроби умножить или разделить на один и тот же многочлен, то получится дробь равная данной.
В виде буквенной формулы основное свойство алгебраической дроби можно записать так:
| a | = | a · c | и | a | = | a : c |
| b | b · c | b | b : c |
где c≠0.
Используя основное свойство алгебраических дробей выполняют их сокращение. Сокращение алгебраических дробей
Чтобы сократить алгебраическую дробь надо числитель и знаменатель разложить на множители. Если числитель и знаменатель имеют общие множители, то дробь можно сократить. Если у числителя и знаменателя общих множителей нет, то дробь является несократимой.
Пример 1. Сократить дробь:
Решение: Разложим числитель и знаменатель на множители, выделим их общий множитель и сократим дробь на него:
| ab2 + bc | = | b(ab + с) | = | ab + с |
| ab2 | b · ab | ab |
Пример 2. Упростить дробь:
Решение: Сначала мы можем сократить дробь на общий множитель x в первой степени:
| 3x (a + b) | = | 3(a + b) |
| x2(b — a) | x(b — a) |
Теперь стоит внимательно посмотреть на многочлены заключённые в скобки:
a + b и b — a
Чтобы многочлен из знаменателя привести к тому же виду, что и у многочлена в числителе, надо поменять у многочлена b — a знак на противоположный и переставить члены местами:
b — a = -(-b + a) = -(a — b)
Теперь и в числителе и в знаменателе у нас есть общий множитель, который можно сократить:
| 3(a + b) | = | 3(a + b) | = — | 3 |
| x(b — a) | —x(a + | x |
Пример 3. Сократите дробь:
Решение: числитель и знаменатель дроби являются одночленами. Каждый одночлен – это произведение, состоящее из множителей, значит можно сразу переходит к сокращению:
- Начинаем с числового множителя. Числовые множители можно сократить на их наибольший общий делитель. Для чисел 24 и 16 – это число 8. После сокращения от 24 останется 3, а от 16 – 2.
- Буквенные множители сокращаем на степень с наименьшим встречающимся показателем:
- a и a5 сокращаем на a. Единицу в числитель не пишем, а в знаменателе остаётся a4.
- b3 и b3 сокращаем на b3, единицы в результат не записываем.
- c5 и c сокращаем на c, в числитель пишем c4 в знаменатель не пишем ничего.
Следовательно:
| 24ab3c5 | = | 3c4 |
| 16a5b3c | 2a4 |
naobumium.info
8 класс. Алгебра. Алгебраические дроби. — Сложение и вычитание алгебраических дробей.
Комментарии преподавателя
В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему – сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров
Сформулируем правило сложения (вычитания) алгебраических дробей с одинаковыми знаменателями (оно совпадает с аналогичным правилом для обыкновенных дробей): То есть для сложения или вычитания алгебраических дробей с одинаковыми знаменателями необходимо составить соответствующую алгебраическую сумму числителей, а знаменатель оставить без изменений.
Это правило мы разберём и на примере обыкновенных дробей, и на примере алгебраических дробей.
Пример 1. Сложить дроби: .
Решение
Сложим числители дробей, а знаменатель оставим таким же. После этого разложим числитель и знаменатель на простые множители и сократим. Получим: .
Примечание: стандартная ошибка, которую допускают при решении подобного рода примеров, заключается в следующем способе решения: . Это грубейшая ошибка, поскольку знаменатель остаётся таким же, каким был в исходных дробях.
Ответ: .
Пример 2. Сложить дроби: .
Решение
Данная задача ничем не отличается от предыдущей:
www.kursoteka.ru
Алгебраические дроби. Сокращение алгебраических дробей в более сложных случаях
Тема: Разложение многочленов на множители
Урок: Алгебраические дроби. Сокращение алгебраических дробей в более сложных случаях
Напомним, что алгебраическая дробь есть отношение многочленов:
В предыдущем уроке мы провели аналогию между алгебраической дробью и арифметической дробью. Напомним:
– результат разложения на множители числителя и знаменателя некоторой дроби;
Конкретно это была дробь
Сократим заданное выражение:
Заменим числа переменными x, y, z, получим:
Напомним, что основная задача при работе с алгебраическими дробями – разложить числитель и знаменатель на множители и если появится такая возможность сократить общие множители.
Рассмотрим примеры:
Пример 1:
Преобразуем числитель с помощью формулы разности квадратов:
Сократим появившийся общий множитель:
В результате деления двучленов получен двучлен, который мы расписали по формуле разности кубов и получили его разложение на множители;
Пример 2:
Разложим на множители числитель и знаменатель. В знаменателе в явном виде стоит формула квадрата суммы, а в числителе под квадратом стоит разность квадратов:
Раскроем квадрат в числителе, для этого каждый множитель возведем в квадрат:
Сократим общий множитель:
Пример 3 – упростить дробь и вычислить ее значение при :
Разложим на множители числитель и знаменатель:
Сократим общий множитель:
Подставим значение и вычислим значение дроби:
Пример 4 – упростить дробь и вычислить ее значение при :
Применим к числителю формулу разности квадратов, а к знаменателю формулу квадрата суммы:
Подставим значение и вычислим:
Пример 5 – разложить на множители:
Применим способ группировки для разложения числителя и знаменателя:
Сократим общий множитель:
Вывод: в данном уроке мы вспомнили, что такое алгебраическая дробь и каковы основы работы с ней. Мы научились решать сложные примеры и закрепили навыки решения заданий с алгебраическими дробями.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет:
1. Вся элементарная математика (Источник).
2. Школьный помощник (Источник).
Рекомендованное домашнее задание:
Задание 1: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 446, ст.152;
Задание 2: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 447, ст.152;
Задание 3: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 448, ст.152;
interneturok.ru
Умножение и деление алгебраических дробей
Умножение дробей
Чтобы умножить одну алгебраическую дробь на другую надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата), и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).
Правило умножения алгебраических дробей в виде формулы:
| a | · | c | = | ac | (b≠0 и d≠0) |
| b | d | bd |
Пример. Выполнить умножение алгебраических дробей:
Решение: перед тем как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители – это поможет сократить алгебраическую дробь, которая получится в результате:
| 2a2 | · | a + b | = | 2a2 | · | a + b | = | 2a2(a + b) |
| a2 — b2 | a | (a + b)(a — b) | a | (a + b)(a — b)a |
теперь сокращаем полученную дробь:
| 2a2(a + b) | = | 2a |
| (a + b)(a — b)a | a — b |
Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.
Пример. Выполнить умножение многочлена на алгебраическую дробь:
Решение:
| (2x + 6) · | x — 2 | = | (2x + 6)(x — 2) |
| x + 3 | x + 3 |
разложим первый многочлен числителя на множители и сократим дробь:
| (2x + 6)(x — 2) | = | 2(x + 3)(x — 2) | = 2(x — 2) = 2x — 4 |
| x + 3 | x + 3 |
Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:
| a · | b | = | ab | или | b | · a | = | ab | (c≠0) |
| c | c | c | c |
Возведение алгебраических дробей в степень
Чтобы возвести в степень алгебраическую дробь надо возвести в эту степень отдельно её числитель и отдельно знаменатель.
Правило возведения алгебраических дробей в степень в виде формулы:
Пример. Выполнить возведение в степень:
| а) ( | a2 | )3 б) (- | 2x3 | )2 |
| b | y2 |
Решение:
| а) ( | a2 | )3 = | (a2)3 | = | a6 |
| b | (b)3 | b3 |
| б) (- | 2x3 | )2 = | (2x3)2 | = | 4x6 |
| y2 | (y2)2 | y4 |
Посмотреть правила возведения степени в степень вы можете на странице Свойства степени
.
Деление дробей
Чтобы разделить одну алгебраическую дробь на другую надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.
Правило деления алгебраических дробей в виде формулы:
| a | : | c | = | a | · | d | = | ad |
| b | d | b | c | bc |
Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.
Пример. Выполнить деление алгебраических дробей:
Решение: переворачиваем делитель и умножаем дроби по правилам умножения:
| ab + ac | : | ab — ac | = | ab + ac | · | bc | = | (ab + ac)bc |
| bc | bc | bc | ab — ac | bc(ab — ac) |
теперь можно приступать к сокращению полученной дроби:
| (ab + ac)bc | = | ab + ac | = | a(b + c) | = | b + c |
| bc(ab — ac) | ab — ac | a(b — c) | b — c |
Чтобы разделить многочлен на алгебраическую дробь надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.
Правило деления многочлена на алгебраическую дробь в виде формулы:
| a : | b | = a · | c | = | ac |
| c | b | b |
Пример. Выполнить деление:
Решение:
| 6xy2 : | x | = 6xy2 · | y | = 6y3 |
| y | x |
Чтобы разделить алгебраическую дробь на многочлен надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.
Правило деления алгебраической дроби на многочлен в виде формулы:
| a | : c = | a | : | c | = | a | · | 1 | = | a |
| b | b | 1 | b | c | bc |
Пример. Выполнить деление:
Решение:
| 2xy | : 6y = | 2xy | : | 6y | = | 2xy | · | 1 | = | 2xy | = | x |
| 3 | 3 | 1 | 3 | 6y | 18y | 9 |
naobumium.info
Сложение и вычитание алгебраических дробей
Сложение и вычитание с одинаковыми знаменателями
Чтобы выполнить сложение или вычитание алгебраических дробей с одинаковыми знаменателями надо найти сумму или разность числителей, а знаменатель оставить без изменений.
Пример 1. Выполните сложение алгебраических дробей:
| а) | a + 3 | + | a — 3 | б) | 2b — 1 | + | b + 4 |
| b | b | 2 | 2 |
Решение: складываем числители дробей и выполняем приведение подобных членов (если они есть):
| а) | a + 3 | + | a — 3 | = | (a + 3) + (a — 3) | = | a + 3 + a — 3 | = | 2a |
| b | b | b | b | b |
| б) | 2b — 1 | + | b + 4 | = | (2b — 1) + (b + 4) | = | 2b — 1 + b + 4 | = | 3b + 3 |
| 2 | 2 | 2 | 2 | 2 |
Пример 2. Выполните вычитание алгебраических дробей:
| а) | x + 5 | — | 5x | б) | a + b | — | a + 4 |
| 3 | 3 | a — 5 | a — 5 |
Решение: вычитаем из числителя первой дроби числитель второй дроби и выполняем приведение подобных членов (если они есть):
| а) | x + 5 | — | 5x | = | x + 5 — 5x | = | 5 — 4x |
| 3 | 3 | 3 | 3 |
| б) | a + b | — | a + 4 | = | (a + b) — (a + 4) | = | a + b — a — 4 | = | b — 4 |
| a — 5 | a — 5 | a — 5 | a — 5 | a — 5 |
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями в виде общих формул:
| a | + | b | = | a + b | и | a | — | b | = | a — b | (c≠0) |
| c | c | c | c | c | c |
Если дроби имеют знаменатели, состоящие из противоположных выражений, то есть выражений, отличающихся только знаком, надо тождественно преобразовать одну из дробей, чтобы привести их к общему знаменателю. Преобразование выполняется в соответствии с правилами знаков:
Данное преобразование можно рассматривать как умножение числителя и знаменателя дроби на -1. Следовательно, если числитель и знаменатель алгебраической дроби заменить на противоположные выражения, то получится дробь равная данной. Полученную дробь можно переписать, поставив один из минусов перед дробью:
| a | = | —a | = — | a | = — | —a |
| b | —b | —b | b |
Также, любую отрицательную дробь можно сделать положительной, перенеся минус, стоящий перед дробью, в числитель или знаменатель:
Пример 1. Найдите сумму дробей:
Решение: чтобы выполнить сложение, поменяем знаки перед второй дробью и в её знаменателе на противоположные:
| 5a | + | 3a | = | 5a | — | 3a | = | 5a | — | 3a | = | 2a |
| b — c | c — b | b — c | -(c — b) | b — c | b — c | b — c |
Пример 2. Найдите разность дробей:
Решение: чтобы выполнить вычитание, перенесём знак минус, стоящий перед второй дробью в её знаменатель:
| n + 5 | — | 2n | = | n + 5 | + | 2n | = | n + 5 | + | 2n | = | 3n + 5 |
| n2 — m | m — n2 | n2 — m | -(m — n2) | n2 — m | n2 — m | n2 — m |
Сложение и вычитание с разными знаменателями
Чтобы найти сумму или разность алгебраических дробей с разными знаменателями надо:
- найти общий знаменатель
- привести алгебраические дроби к общему знаменателю
- выполнить сложение или вычитание
- сократить полученную дробь, если это возможно
Пример 1. Выполните сложение дробей:
Решение: находим общий знаменатель, он будет равен произведению знаменателей данных дробей:
(a + b)(a — b)
Как находить общий знаменатель вы можете узнать на странице Приведение алгебраических дробей к общему знаменателю
. Далее умножаем числитель каждой дроби на дополнительный множитель:
2a(a — b) = 2a2 — 2ab
b(a + b) = ab + b2
Общий знаменатель можно свернуть в разность квадратов. В итоге у нас получится:
| 2a | + | b | = | 2a2 — 2ab | + | ab + b2 | = |
| a + b | a — b | a2 — b2 | a2 — b2 |
| = | 2a2 — 2ab + ab + b2 | = | 2a2 — ab + b2 |
| a2 — b2 | a2 — b2 |
Пример 2. Выполните вычитание дробей:
Решение: разложим знаменатель первой дроби на множители:
a2 — ab = a(a — b)
Так как данное выражение делится на знаменатель второй дроби, то возьмём его в качестве общего знаменателя. Значит теперь нам надо умножить числитель второй дроби на дополнительный множитель a:
2 · a = 2a
Получаем:
| b | — | 2 | = | b | — | 2a | = | b — 2a |
| a2 — ab | a — b | a(a — b) | a(a — b) | a(a — b) |
Пример 3. Выполните сложение:
Решение: запишем первое слагаемое в виде дроби и приведём её к знаменателю 1 — x:
| x + | x2 | = | x | + | x2 | = | x(1 — x) | + | x2 | = | x — x2 | + | x2 |
| 1 — x | 1 | 1 — x | 1 — x | 1 — x | 1 — x | 1 — x |
Теперь можно выполнить сложение дробей с одинаковыми знаменателями:
| x — x2 | + | x2 | = | x — x2 + x2 | = | x |
| 1 — x | 1 — x | 1 — x | 1 — x |
Точно также можно выполнять сложение и вычитание алгебраических дробей с любыми многочленами.
naobumium.info
Задание №7 Действия с алгебраическими дробями
Задание № 7
Действия с алгебраическими дробями
Сложение и вычитание алгебраических дробей:
С одинаковыми знаменателями выполняется по правилу:
С разными знаменателями: Привести все дроби к общему знаменателю; если они с самого начала имели одинаковые знаменатели, то этот шаг алгоритма опускают. Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями.
Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей: Разложить все знаменатели на множители.
Из первого знаменателя выписать произведение всех его
множителей, из остальных знаменателей приписать к этому
произведению недостающие множители. Полученное произведение
будет общим знаменателем.
Найти дополнительные множители для каждой из дробей.
Записать каждую дробь с новым числителем и общим знаменателем.
Умножение и деление алгебраических дробей:

 .
.
Пример:
1. ;
2. 3.
Тренировочные упражнения:
Выполни действия:
1)  ;
2)
;
2)  ;
3)
;
3)  ;
4)
;
4)  ;
;
5)  ;
6)
;
6)  7)
7)  8)
8)  .
.
Контрольные задания:
Выполни действия:
1) 
а)  б)
б)  в)
в)  г)
г) 
2) 
a)  б)
б)  в)
в)  г)
г) 
3) 
a)  б)
б) 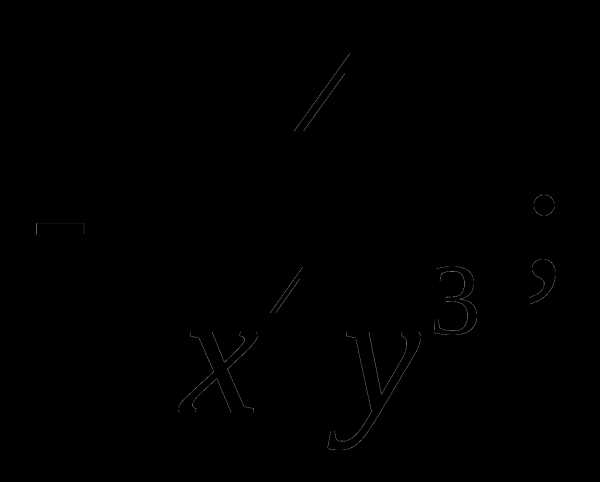 в)
в)  г)
г) 
4) 
a)  б)
б)  в)
в)  г)
г) 
5) 
a)  б)
в)
б)
в)  г)
г)
6) 
a)  б)
б)  в)
в) 
 г)
г) 
Ответы: 1) б;
2) а;
3) г;
4) в;
5) б;
6) в.
gigabaza.ru


 .
.