Как умножить число на дробь
Правило умножения числа на дробь несложное:
Чтобы умножить число на дробь, надо числитель умножить на это число, а знаменатель оставить тем же.
Рассмотрим, как умножить число на дробь, на конкретных примерах.
Решение:
Чтобы умножить дробь на число, числитель умножаем на это число, а знаменатель оставляем без изменения. Сократить здесь ничего нельзя.
Чтобы умножить число на дробь, числитель умножаем на это число, а знаменатель оставляем тем же. 5 и 35 сокращаем на 5. Получаем правильную дробь, значит это — окончательный ответ.
Здесь также умножаем числитель на число, а знаменатель не изменяем. 12 и 9 сокращаем на 3. Полученная при умножении дробь — неправильная. Выделяем целую часть.
Как умножить число на дробь, если число больше знаменателя? Все по тому же правилу: числитель умножаем на число, знаменатель переписываем. 16 и 32 умножаем на 16. Поскольку в результате знаменатель равен единице, его не пишем. Ответ — целое число.
www.for6cl.uznateshe.ru
Умножение дробей | Математика
Умножение дробей — тема, включающая в себя действия с обыкновенными дробями, смешанными числами, десятичными дробями.
Запишем на одной странице все правила, касающиеся умножения обыкновенных дробей, смешанных и натуральных чисел.
1. Умножение обыкновенных дробей.
Чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель — на знаменатель.
Произведение числителей записывают в числитель, знаменателей — в знаменатель. Если возможно, дроби следует сократить. Проще сокращать множители, чем результат.
Примеры умножения обыкновенных дробей:
2. Умножение обыкновенной дроби на натуральное число.
Чтобы умножить обыкновенную дробь на натуральное число, надо числитель умножить на это число, а знаменатель оставить тем же.
Если возможно, дробь следует сократить. Если в результате получили неправильную дробь, нужно выделить из неё целую часть.
Примеры умножения обыкновенной дроби на натуральное число:
3. Умножение смешанных чисел.
Чтобы умножить смешанные числа, надо перевести их в неправильные дроби и применить правило умножения обыкновенных дробей.
Примеры умножения смешанных чисел:
Примеры умножения смешанного числа и обыкновенной дроби:
4. Умножение смешанного числа на натуральное число.
1) Чтобы смешанное число умножить на натуральное, можно смешанное число перевести в неправильную дробь и применить правило умножения дроби на натуральное число.
Примеры умножения смешанного числа на натуральное число по первому правилу:
2) Чтобы умножить смешанное число на натуральное, можно отдельно умножить на это число целую часть, отдельно — дробную, и полученные произведения сложить.
Примеры умножения смешанного и натурального чисел по второму правилу:
В следующий раз рассмотрим все правила, касающиеся умножения десятичных дробей.
www.for6cl.uznateshe.ru
умножение десятичной дроби на натуральное число
Записи с меткой «умножение десятичной дроби на натуральное число»
I. Чтобы умножить десятичную дробь на натуральное число, нужно умножить ее на это число, не обращая внимания на запятую, и в полученном произведении отделить запятой столько цифр справа, сколько их было после запятой в данной дроби.
Примеры. Выполнить умножение: 1) 1,25·7; 2) 0,345·8; 3) 2,391·14.
Решение.
Смотрите видео: « Как умножить десятичную дробь на натуральное число».
II. Чтобы умножить одну десятичную дробь на другую, нужно выполнить умножение , не обращая внимания на запятые, и в полученном результате отделить запятой справа столько цифр, сколько их было после запятых в обоих множителях вместе.
Примеры. Выполнить умножение: 1) 18, 2·0,09; 2) 3,2·0,065; 3) 0,54·12,3.
Решение.
Смотрите видео: «Умножение десятичных дробей.»
III. Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 3,25·10; 2) 0,637·100; 3) 4,307·1000; 4) 2,04·1000; 5) 0,00031·10000.
Решение.

Смотрите видео: «Умножение десятичных дробей на 10, 100, 1000 и т. д.»
IV. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.
Примеры. Выполнить умножение: 1) 28,3·0,1; 2) 324,7·0,01; 3) 6,85·0,01; 4) 6179,5·0,001; 5) 92,1·0,0001.
Решение.
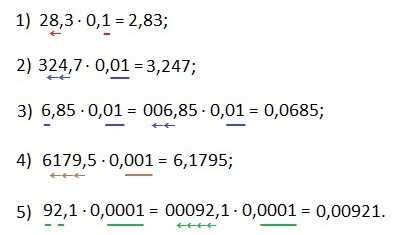
Смотрите видео: «Умножение десятичных дробей на 0,1; 0,001; 0,0001 и т. д.»
www.mathematics-repetition.com
Умножение дробей
Умножение обыкновенных дробей
Чтобы умножить две дроби нужно выполнить следующие шаги:
- 1 Перемножить числители дробей между собой 5 × 6 = 30.
- 2 Перемножить знаменатели дробей между собой 8 × 7 = 56.
- 3 Сократим полученную дробь , в результате получим .
Нахождения произведения дробей можно записать в виде:
При умножение дробей не имеет значения, имеют ли они одинаковый знаменатель или разный.
Пример Найти произведение дробей
.
Чтобы проверить результат умножения дробей, можно воспользоваться калькулятором дробей.
Пример Умножить дроби .
.
Умножение дроби на число
Чтобы умножить дробь на число, нужно умножить число на числитель, а знаменатель оставить без изменения.
Пример Умножить число на дробь
.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
calcs.su
Как умножить десятичную дробь на число
Рассмотрим, как умножить десятичную дробь на натуральное число.
Правило умножения числа на десятичную дробь
Чтобы умножить десятичную дробь на натуральное число:
1) Умножаем числа, не обращая внимания на запятую.
2) В результате отделяем после запятой столько цифр, сколько их после запятой в десятичной дроби.
Примеры.
Выполнить умножение десятичных дробей на натуральные числа:
1) 12,3∙4;
2) 34,07∙3;
3) 0,54∙25;
4) 52,783∙34;
5) 0,00078∙12.
Решение:
1) 12,3∙4=?
Чтобы умножить десятичную дробь 12,3 на натуральное число 4, сначала умножаем эти числа, не обращая внимания на запятую, то есть умножаем 123 на 4: 123∙4=492.
В полученном произведении отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 12,3, то есть одну цифру: 49,2. Таким образом, 12,3∙4=49,2.
2) 34,07∙3=?
Умножаем числа, не обращая внимания на запятую: 3407∙3=10221.
В результате отделяем после запятой столько цифр, сколько их в десятичной дроби 34,07, то есть две: 102,21.
Таким образом, 34,07∙3=102,21.
3) 0,54∙25=?
Сначала умножим эти числа, не принимая во внимания запятую: 54∙25=1350.
Затем отделяем после запятой столько цифр, сколько их после запятой в десятичной дроби 0,54, то есть две цифры: 13,50. В конце записи после запятой стоит нуль, его следует отбросить:
0,54∙25=13,50=13,5.
4) 52,783∙34=?
Умножаем числа, отбросив запятую: 52783∙34=1794622.
Так как в записи десятичной дроби 52,783 после запятой стоит три цифры, в полученном произведении после запятой также должно стоять три цифры: 1794,622.
Итак, 52,783∙34=1794,622.
5) 0,00078∙12=?
Умножение десятичной дроби на натуральное число заменяем умножением натуральных чисел: 78∙12=936.
Теперь нужно отделить после запятой столько цифр, сколько их после запятой в десятичной дроби 0,00078, то есть пять цифр: 0,00936.
В результате имеем: 0,00078∙12=0,00936.
Поскольку от перемены мест множителей произведение не меняется (переместительное свойство умножения), умножение числа на натуральную дробь проводят точно так же.
Примеры.
Выполнить умножение натуральных чисел на десятичные дроби:
1) 958∙0,007;
2) 31∙0,000046;
Решение:
1) 958∙0,007=?
Умножаем натуральные числа 958 и 7 ( то есть не обращаем внимания на запятую): 958∙7= 6706.
В полученном произведении отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 0,007, то есть три цифры: 6,706.
Таким образом, 958∙0,007=6,706.
2) 31∙0,000046=?
Умножение числа на десятичную дробь заменяем умножением натуральных чисел: 31∙46=1426.
В результате отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 0,000046, то есть шесть цифр: 0,001426 (недостающее количество цифр дополняем двумя нулями и перед запятой также пишем нуль).
Итак, 31∙0,000046=0,001426.
Для умножения десятичных дробей на 10, 100, 1000 и т.д. проще использовать другие правила.
www.for6cl.uznateshe.ru
Как умножать дроби | Математика
Правило умножения обыкновенных дробей простое, и его несложно запомнить:
Чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель — на знаменатель.
Эта формула наглядно показывает, как умножать дроби:
Если это возможно, то дробь сокращаем. Причем сокращать проще множители, а не готовый результат.
Теперь рассмотрим, как умножать дроби, на конкретных примерах.
Решение:
здесь сократить ничего нельзя, поэтому просто умножаем числитель на числитель, знаменатель — на знаменатель и получаем окончательный результат.
Семерки сокращаем на 7, 3 и 12 — на 3. Оставшиеся после сокращения результаты перемножаем.
Здесь 15 и 45 сокращаем на 15, а 34 и 17 — на 17.
В этом примере 14 и 35 сокращаем на 7, а 18 и 27 — на 9. Остается перемножить числа, полученные при сокращении.
В следующий раз рассмотрим, как дробь умножить на целое число.
www.for6cl.uznateshe.ru
Правила умножения дробей
Для того чтобы произвести арифметические действия умножения над дробями, следует перемножить их числители и знаменатели, а результат записать в соответствующей форме.
Умножение простой дроби на числоПри умножении простой дроби на натуральное число, ее числитель следует умножить на этот множитель, а знаменатель оставить без изменения.
3 8 |
× | 4 | = | 3 × 4 8 |
= | 12 8 |
= | 1 | 4 8 |
= | 1 | 1 2 |
При необходимости умножения смешанной дроби на натуральное число следует произвести данное арифметическое действие с целым числом этой дроби и её числителем.
| 1 | 2 5 |
× | 3 | = | 1 × 3 | + | 2 × 3 5 |
= | 3 | 6 5 |
= | 4 | 1 5 |
Когда нужно умножить простую дробь на простую дробь, следует перемножить числители, а затем знаменатели.
3 6 |
× | 4 8 |
= | 3 × 4 6 × 8 |
= | 12 48 |
= | 1 4 |
При выполнении операции умножения смешанных чисел, их следует записать в виде неправильных дробей, после чего перемножить их по соответствующим правилам.
| 2 | 1 3 |
× | 4 | 3 5 |
= | 7 3 |
× | 23 5 |
= | 7 × 23 3 × 5 |
= | 161 15 |
= | 10 | 11 15 |
simple-math.ru
