Способы задания множеств
I. Перечисление (список элементов).
II. Порождающая процедура.
III. Разрешающая процедура (описание характеристических свойств, которыми должны обладать элементы).
I. Задание множества списком
Списком можно задать лишь множества, содержащие несколько элементов. Задание типа
N = 1, 2, 3 . . .
не список, а условное обозначение, допустимое, когда оно заведомо не вызывает разногласий.
Пример:
Определим А как множество все целых чисел х строго между 6 и 10. Это можно записать следующим образом:
и прочитать как : “А — множество, содержащее 7, 8, 9”.
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например,
.
Мы не делаем никакой оговорки о порядке, в котором рассматриваются элементы, поэтому было бы неправильно допускать какой-либо определенный порядок.
Выясним далее, какие из приведенных определений верные:
.
Если число членов множества В легко вычисляется, и среди элементов множества нет повторений, то определение верно.
Множество С также выглядит правильным, за исключением лишь того, что число 6 повторяется дважды. Мы можем проверить, принадлежит ли элемент или нет. Таким образом, это наиболее важное требование в определении множества выполнено. Следовательно, мы можем рассматривать эту запись как верную и эквивалентную . Однако в этой ситуации возникают следующие проблемы. Если мы рассмотрим первоначальное определение С и выбросим одно из чисел 6 из множества, то мы, очевидно, будем иметь и. Возникает противоречие. Поэтому мы будем рассматривать повторение символов в определении множеств как упоминание одного и того же символа, а его дублирование как недосмотр.
Определение D также справедливо. Заметим, что это множество множеств, такое, что оно имеет только два элемента, в частности, , даже еслии. Это легко проверить, так каки только В и С являются элементами D.
II. Порождающая процедура
Описывает способ получения элементов множества из уже полученных элементов либо других объектов. Тогда элементы множества — все объекты, которые могут быть получены (построены) с помощью такой процедуры.
Примеры:
1) Описание множества (множество всех чисел вида), где исходные объекты для построения множества — натуральные числа, а порождающая процедура для вычисления описана формулой.
Порождающая процедура определяется двумя правилами:
а) ; б) если, то.
Правила, описанные таким образом, называются индуктивными или рекурсивными.
3) Множество , заданное следующим образом.
Пусть имеется процедура вычисления цифр разложения числа в бесконечную десятичную дробь
= 3,1415926536 . . .
По мере вычисления будем образовывать из последовательности цифр данной десятичной дроби трехзначные числа
314, 159, 265 и т. д.
Множество всех таких чисел образует множество .
4) Распространенная порождающая процедура — образование новых множеств из других множеств с помощью операций над множествами.
III. Задание множества описанием его элементов (разрешающая процедура)
Примеры:
— множество всех натуральных чисел (N).
— множество всех решений уравнения .— множество всех действительных чисел.
— множество всех чисел , гдеможно интерпретировать как описание свойства его элементов, заключающегося в возможности представить их в виде.
— заданное как “множество всех целых чисел, являющихся степенью двойки”, . Такой способ задания множества применяется, когда свойство элементов М может быть описано коротким выражением. Например, P(x) читается: «х обладает свойством Р», то М задается при помощи обозначениячитается: «М — множество элементов х, обладающих свойством Р».
Пример:
1) .
2) .
Требования к описанию свойств — точность и недвусмысленность.
Пример:
Множество всех красивых первокурсниц математического факультета 2002 г. не строго определено, так как у разных людей – различные критерии отбора.
Надежный способ точно описать свойства элементов данного множества — задание распознающей (разрешающей) процедуры, которая для любого объекта устанавливает, обладает он свойством или нет (т. е. является элементом множества или нет).
Пример:
Для , то есть для свойства, быть степенью двойкиразрешающей процедурой является любой метод разложения целых чисел на простые множители. Здесь разрешающая процедура не является порождающей. Но ее нетрудно таковой сделать: например, порождающая процедура может быть таковой. Берем последовательно все натуральные числа и каждые из них разлагаем на простые множители: те числа, которые не содержат множителей, отличных от двойки, включаем в .
С другой стороны порождающая процедура может не быть разрешающей. Например, при получении действует порождающая процедура. Но с ее помощью нельзя определить, будет ли произвольное трехзначное число принадлежатьили нет, т. е. множествобесконечно, и если при построении n — чисел множества некоторое (проверяемое) число не встретилось, то еще нельзя утверждать, что оно не принадлежит.
Обобщение: Суть порождающей процедуры в том, что с ее помощью из уже полученных элементов множества или других объектов получают (или могут получить) все последующие элементы.
Суть разрешающей процедуры в том, что она разрешает (или не разрешает) предложенному для проверки объекту быть или не быть элементом данного множества в зависимости от его свойств.
Понятие “точно заданное множество” нуждается в уточнении. Одна из основных трудностей задания множества (даже из множеств, точность описания которых не вызывает сомнения) с помощью вполне, казалось бы, законных средств — в том, что можно сконструировать описание множеств, которые приводят к противоречиям — “парадоксам теории множеств”. Например, множество всех подмножеств по смыслу своего описания этого множества должно содержать все мыслимые множества. Но оно само содержится в множестве своих подмножеств в качестве элемента.
Перед дальнейшим изложением будет удобно определить два специальных множества.
Определение: Пустое множество (обозначается ) есть множество, обладающее свойством:
при любом х.
Другое множество, определение которого зависит от задачи, называют универсальным множеством.
Определение: Универсальное множество (обозначается U) есть множество всех рассматриваемых в данной задаче элементов.
Рассмотрим теперь множество. Оно имеет n элементов. Будем говорить, что мощность этого множества есть n.
Определение: Мощностью (длиной, размерностью) множества называется число элементов этого множества. Обозначим .
Далее любое множество В, которое имеет то же число элементов, что и А, имеет такую же мощность, и естественно, эти элементы не надо пересчитывать. Для небольших множеств достаточно легко пересчитать элементы, но для других множеств, например N, это может быть невозможно. Далее следует строгое, но неформальное определение количества элементов.
Определение: Говорят, что множество Х конечно, если или для некоторогосуществует множествотакое, что оно имеет то же самое число элементов, что и X. Еслии никакого n не может быть найдено, то Х называютбесконечным.
studfiles.net
Способы задания множеств
I. Перечисление (список элементов).
II. Порождающая процедура.
III. Разрешающая процедура (описание характеристических свойств, которыми должны обладать элементы).
I. Задание множества списком
Списком можно задать лишь множества, содержащие несколько элементов. Задание типа
N = 1, 2, 3 . . .
не список, а условное обозначение, допустимое, когда оно заведомо не вызывает разногласий.
Пример:
Определим А как множество все целых чисел х строго между 6 и 10. Это можно записать следующим образом:
и прочитать как : “А — множество, содержащее 7, 8, 9”.
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например,
.
Мы не делаем никакой оговорки о порядке, в котором рассматриваются элементы, поэтому было бы неправильно допускать какой-либо определенный порядок.
Выясним далее, какие из приведенных определений верные:
.
Если число членов множества В легко вычисляется, и среди элементов множества нет повторений, то определение верно.
Множество С также выглядит правильным, за исключением лишь того, что число 6 повторяется дважды. Мы можем проверить, принадлежит ли элемент или нет. Таким образом, это наиболее важное требование в определении множества выполнено. Следовательно, мы можем рассматривать эту запись как верную и эквивалентную . Однако в этой ситуации возникают следующие проблемы. Если мы рассмотрим первоначальное определение С и выбросим одно из чисел 6 из множества, то мы, очевидно, будем иметь и. Возникает противоречие. Поэтому мы будем рассматривать повторение символов в определении множеств как упоминание одного и того же символа, а его дублирование как недосмотр.
Определение D также справедливо. Заметим, что это множество множеств, такое, что оно имеет только два элемента, в частности, , даже еслии. Это легко проверить, так каки только В и С являются элементами D.
II. Порождающая процедура
Описывает способ получения элементов множества из уже полученных элементов либо других объектов. Тогда элементы множества — все объекты, которые могут быть получены (построены) с помощью такой процедуры.
Примеры:
1) Описание множества (множество всех чисел вида), где исходные объекты для построения множества — натуральные числа, а порождающая процедура для вычисления описана формулой.
2) Множество
Порождающая процедура определяется двумя правилами:
а) ; б) если, то.
Правила, описанные таким образом, называются индуктивными или рекурсивными.
3) Множество , заданное следующим образом.
Пусть имеется процедура вычисления цифр разложения числа в бесконечную десятичную дробь
= 3,1415926536 . . .
По мере вычисления будем образовывать из последовательности цифр данной десятичной дроби трехзначные числа
314, 159, 265 и т. д.
Множество всех таких чисел образует множество .
4) Распространенная порождающая процедура — образование новых множеств из других множеств с помощью операций над множествами.
III. Задание множества описанием его элементов (разрешающая процедура)
Примеры:
— множество всех натуральных чисел (N).
— множество всех решений уравнения .
— множество всех действительных чисел.
— множество всех чисел , гдеможно интерпретировать как описание свойства его элементов, заключающегося в возможности представить их в виде.
— заданное как “множество всех целых чисел, являющихся степенью двойки”, . Такой способ задания множества применяется, когда свойство элементов М может быть описано коротким выражением. Например, P(x) читается: «х обладает свойством Р», то М задается при помощи обозначениячитается: «М — множество элементов х, обладающих свойством Р».
Пример:
1) .
2) .
Требования к описанию свойств — точность и недвусмысленность.
Пример:
Множество всех красивых первокурсниц математического факультета 2002 г. не строго определено, так как у разных людей – различные критерии отбора.
Надежный способ точно описать свойства элементов данного множества — задание распознающей (разрешающей) процедуры, которая для любого объекта устанавливает, обладает он свойством или нет (т. е. является элементом множества или нет).
Пример:
Для , то есть для свойства, быть степенью двойкиразрешающей процедурой является любой метод разложения целых чисел на простые множители. Здесь разрешающая процедура не является порождающей. Но ее нетрудно таковой сделать: например, порождающая процедура может быть таковой. Берем последовательно все натуральные числа и каждые из них разлагаем на простые множители: те числа, которые не содержат множителей, отличных от двойки, включаем в .
С другой стороны порождающая процедура может не быть разрешающей. Например, при получении действует порождающая процедура. Но с ее помощью нельзя определить, будет ли произвольное трехзначное число принадлежатьили нет, т. е. множествобесконечно, и если при построении n — чисел множества некоторое (проверяемое) число не встретилось, то еще нельзя утверждать, что оно не принадлежит.
Обобщение: Суть порождающей процедуры в том, что с ее помощью из уже полученных элементов множества или других объектов получают (или могут получить) все последующие элементы.
Суть разрешающей процедуры в том, что она разрешает (или не разрешает) предложенному для проверки объекту быть или не быть элементом данного множества в зависимости от его свойств.
Понятие “точно заданное множество” нуждается в уточнении. Одна из основных трудностей задания множества (даже из множеств, точность описания которых не вызывает сомнения) с помощью вполне, казалось бы, законных средств — в том, что можно сконструировать описание множеств, которые приводят к противоречиям — “парадоксам теории множеств”. Например, множество всех подмножеств по смыслу своего описания этого множества должно содержать все мыслимые множества. Но оно само содержится в множестве своих подмножеств в качестве элемента.
Перед дальнейшим изложением будет удобно определить два специальных множества.
Определение: Пустое множество (обозначается ) есть множество, обладающее свойством:
при любом х.
Другое множество, определение которого зависит от задачи, называют универсальным множеством.
Определение: Универсальное множество (обозначается U) есть множество всех рассматриваемых в данной задаче элементов.
Рассмотрим теперь множество. Оно имеет n элементов. Будем говорить, что мощность этого множества есть n.
Определение: Мощностью (длиной, размерностью) множества называется число элементов этого множества. Обозначим .
Далее любое множество В, которое имеет то же число элементов, что и А, имеет такую же мощность, и естественно, эти элементы не надо пересчитывать. Для небольших множеств достаточно легко пересчитать элементы, но для других множеств, например N, это может быть невозможно. Далее следует строгое, но неформальное определение количества элементов.
Определение: Говорят, что множество Х конечно, если или для некоторогосуществует множествотакое, что оно имеет то же самое число элементов, что и X. Еслии никакого n не может быть найдено, то Х называютбесконечным.
studfiles.net
Множества. способы задания множеств — математика, уроки
ПрактическАЯ РАБОТА
Тема: Множества. Способы задания множеств.
Цели:
ознакомиться с понятием множества;
ознакомиться со способами задания множеств;
ознакомиться с основными видами множеств.
Оснащение занятия: конспект лекций.
Порядок выполнения работы
Задание 1.
1. Ознакомиться с лекцией 1.
2. Выписать в тетрадь определения. Ответить на вопросы:
а). Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.
б). Что значит задать множество?
в). Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.
г). Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.
д). Дайте определение характеристического свойства элементов множества.
3. Записать в тетрадь образцы решения заданий
Лекция 1.
Тема «Множества. Способы задания множеств»
Множества.
Множество — совокупность различных элементов, мыслимая как единое целое. Элемент множества — объект А называется элементом множества, если он обладает характеристическим свойствами этого множества.
Способы задания множеств.
1) Перечислением — при перечислении множества его элементы принято заключать в фигурные скобки:
{2,4,6,…} — множество четных чисел,
{3,6,9,…}— множество чисел кратных трем.
Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.
2) Описание свойств — для задания (описания) некоторого множества
X, состоящего из элементов, обладающих свойством α, используют запись X={x |α(x)}. Читается как: «X — множество элементов x таких, что α(x)». Например, Y={y | y∈N и y — множество натуральных чисел, меньших 7.
Характеристическое свойство множеств.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.
Равные множества, подмножества.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи:
{a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}.
Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:
Универсальное множество.
Определение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области.
Конечные и бесконечные множества.
Множества, состоящие из бесконечного числа элементов, называются бесконечными, из конечного – конечными.
Пустое множество.
Множество, не содержащее ни одного элемента, называется пустым. ∅
Основные числовые и геометрические множества.
Z− множество целых чисел;
Q− множество рациональных чисел;
I− множество иррациональных чисел;
R− множество действительных чисел;
C− множество комплексных чисел.
Образцы решения заданий
Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.
Ответ: .
Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:
. Ответ: М = {1; 2; 3; 4}.
Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:
Примеры для самостоятельного решения.
Задание 2. Выполните указанные примеры.
Приведите примеры множеств, составленных из объектов следующих видов:
а) неодушевленных предметов;
б) животных;
в) растений;
г) геометрических фигур;
д) населенных пунктов;
е) водоемов;
ж) политических деятелей.
2. Назовите элементы, принадлежащие множеству:
а) студентов вашей группы;
б) предметов, изучаемых в I семестре вашей специальности;
в) всех частей света;
г) субъектов федерации, входящих в Российскую Федерацию.
3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:
а) восьмиугольник;
б) параллелограмм;
в) отрезок;
г) параллелепипед;
д) круг;
е) полукруг?
4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?
5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:
а) 270 N; ж) -3 Z;
б) 0 N; з) Q;
в) –3 N; и) R;
г) 1 Q; к) sin 2,3 R;
д) –7 N; л) tg R.
е) 22 N;
6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?
а) Франция Е; з) Волга Е;
б) Испания Е; и) Нигерия А;
в) Монголия А; к) Гималаи А;
г) Индия А; л) Япония А;
д) Ирак Е; м) Альпы Е;
е) Турция А; н) Швеция А.
ж) Байкал А;
7. Запишите перечислением элементов следующие множества:
а) А – множество нечетных чисел на отрезке [1; 15];
б) В – множество натуральных чисел, меньших 8;
в) С – множество натуральных чисел, больших 10, но меньших 12;
г) D – множество двузначных чисел, делящихся на 10;
д) Е – множество натуральных делителей числа 18;
е) F – множество чисел, модуль которых равен .
8. Запишите перечислением элементов следующие множества:
а) множество различных букв в слове «головоломка»;
б) множества цифр числа 134433154.
9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x:
а) x 5,3;
б) x ≤ –3,8;
в) – 4,5 ≤ x
г) 2,7 ≤ x ≤ 9.
10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:
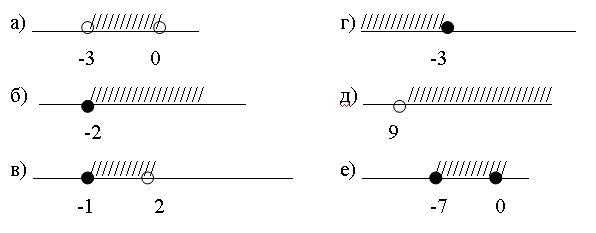
11. Найдите длину каждого из следующих множеств и назовите их элементы:
а) {а}; б) {{а}}; в) ; г) {}; д) {{ a; b }, { а }}; е) {{ a; b; c}, а };
ж) {{ а }, а, }.
2) Из каких элементов состоят следующие множества:
а) множество трехзначных чисел, составленных с помощью цифр 1 и 3;
б) множество трехзначных чисел, составленных с помощью цифр 1, 3, 5, причем так, что никакие две цифры не встречаются дважды;
в) множество трехзначных чисел, составленных из цифр 1, 3, 5 так, что любые две соседние цифры различны;
г) множество трехзначных чисел, сумма цифр которых равна 5.
3) Задайте перечислением элементов множество делителей числа 36. Можно ли задать таким образом множество чисел, кратных числу 36?
Контроль знаний обучающихся:
kopilkaurokov.ru
2.Способы задания множества
Множество можно задать, перечислив все его элементы.
Например, множество А состоит из чисел 3, 4, 5 и 6. Поскольку все его элементы окажутся перечисленными, то это множество задано. При этом возможна запись А = 3, 4, 5, 6, в которой перечисленные элементы заключаются в фигурные скобки.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно, таким образом, и задать конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множеств: указывают характеристическое свойство его элементов.
Определение. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Пример
Множество А – двузначных чисел. Свойство, которым обладает любой элемент данного множества, — “быть двузначным числом”. Это характеристическое свойство дает возможность решить вопрос о том, принадлежит ли какой-либо объект множеству А или не принадлежит. Так, число 21 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит – оно не является двузначным.
Иногда одно и тоже множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными сторонами и как множество ромбов с прямыми углами.
Вывод: чтобы задать некоторое множество, достаточно либо перечислить все его элементы, либо указать характеристическое свойство его элементов. Второй способ более общий: он позволяет задавать и конечные и бесконечные множества в отличие от первого способа, который, как правило, можно использовать для задания конечных множеств с небольшим количеством элементов. Хотя первый способ используется иногда и для задания бесконечных множеств. Например, множество натуральных чисел может быть задано в виде = 1, 2, 3, …. Однако такой способ записи возможен лишь тогда, когда по записанной части множества ясно, что означает многоточие.
Одно и тоже множество может быть задано и первым и вторым способом.
Пример
Множество В натуральных чисел, меньших 7, заданное посредством указания характеристического свойства его элементов, можно задать и так: В=1,2,3,4, 5, 6, т.е. перечислив все его элементы.
3. Отношения между множествами. Подмножество
Даны два множества:
А = a, b, c, d, e и B = b, d, k, e. Видим, что элементы b и d принадлежат одновременно множеству А и множеству В. Говорят, что b и d – общие элементы множеств А и В, а сами множества пересекаются.
Замечание. Если множества не имеют общих элементов, то говорят, что они не пересекаются.
Рассмотрим теперь множества А = a, b, c, d, e и В = c, d, e. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. В этом случае говорят, что множество В включено в А или что множество В является подмножеством множества А.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А.
Если В – подмножество множества А, то пишут: В А – и читают: «В – подмножество А», «В – включается в А».
Считают, что пустое множество является подмножеством любого множества, т. е. А, и что любое множество является подмножеством самого себя, т.е. А А. Поэтому среди всех подмножеств заданного множества А должно быть обязательно пустое множество и само множество А.
studfiles.net
Способы задания множества
Произвольные множества будем обозначать прописными, а элементы множества — строчными буквами латинского алфавита, пустое множество — символом Ø.
Существуют два различных способа задания множества. Можно дать полный перечень элементов этого множества. Этот способ называется перечислением множества. Элементы перечисляемого множества заключают обычно в фигурные скобки. Например, множество А, состоящее из букв русского алфавита, вместе с пробелом (его обозначают знаком ∆) запишется так: А = {а, б, в, …, ю, я, ∆}. Множество студентов учебной группы определяется списком в соответствующем журнале. Понятно, что этот способ задания множества применим только для конечных множеств. Обычно его используют в тех случаях, когда число элементов множества не очень велико.
Другой способ состоит в том, что задается свойство, которым обладает каждый элемент, принадлежащий рассматриваемому множеству, и не обладает ни один элемент, ему не принадлежащий. Этот способ называют описанием множества, а свойство, определяющее множество, характеристическим.
При описании множеств используются различные символы, операции. Если A есть некоторое множество, а x — входящий в него объект, то символическая запись x A означает, что x является элементом множества A; при этом говорят: «x входит в А», «x принадлежит А». Если x не принадлежит множеству А, то пишут x А. Пусть, например, А есть множество букв русского алфавита, тогда, обозначив букву д как элемент х, а букву d как элемент y, можно записать х A, y А. В том случае, когда речь идет о нечетком множестве, указывается степень достоверности, с которой x принадлежит множеству A, Это выражается записью P (x A). Например, пусть A — множество юношей, а x обозначает девятнадцатилетнего мужчину; тогда, исходя из приведенных выше рассуждений, можно записать 0,5 (x A).
Отношения между множествами
Чтобы наглядно изображать множества и отношения между ними, английский математик Джон Венн (1834 — 1923) предложил использовать замкнутые фигуры на плоскости. Намного раньше Леонард Эйлер (1707 — 1783) для этих целей использовал круги, при этом точки внутри круга считались элементами множества. Такие изображения сейчас называют диаграммами Эйлера — Венна.
Пусть даны два произвольных множества A и B, тогда возможны пять случаев отношений между ними:
Множества A и B не имеют общих элементов (см. рис. 1а).
Множества A и B имеют общие элементы, но не все элементы множества A принадлежат множеству B , и не все элементы множества B принадлежат множеству A. В этом случае говорят о пересечении множеств A и B (см. рис. 1б).
Все элементы множества B принадлежат множеству A, но не все элементы множества А принадлежат множеству В. В этом случае говорят о включении множества В во множество А (см. рис. 1в).
Определение: Если имеются два множества A и B, причем каждый элемент множества В принадлежит множеству А, то множество В называется подмножеством множества А. Записывается это так: В А.
Само множество A и пустое множество Ø называют несобственными подмножествами множества А. Все остальные подмножества называются собственными.
Все элементы множества A принадлежат множеству B, но не все элементы множества B принадлежат множеству A. В этом случае говорят о включении множества A во множество B (А В) (см. рис. 1г).
Все элементы множества A принадлежат множеству B и все элементы множества B принадлежат множеству A. В этом случае говорят, что множества A и B равны (см. рис. 1д).
Определение: а) Два множества A и B называются равными (или совпадающими), если А В и В А.
б) Два множества A и B называются равными, если они состоят из одних и тех же элементов. Записывается это так: А = В.
а)
б)
в)
г)
д)
Рис. 1
Определение: Множество, относительно которого все множества, рассматриваемые в данной задаче, являются подмножествами, называется универсальным. Универсальное множество будем обозначать буквой U.
Упражнения: Ответьте, какой из ситуаций, отображенных на рисунке 1, соответствуют отношения множеств, описанных ниже.
А — множество успевающих студентов и В — множество участников художественной самодеятельности.
А — множество студентов-юношей и В — множество студенток.
А — множество отличников учебной группы и В — множество всех студентов этой же учебной группы.
Какое соотношение между множеством успевающих студентов юридического факультета (А) и множеством всех студентов того же факультета (В) является мечтой деканата этого факультета.
В — множество студентов, присутствующих на лекции и А — множество всех студентов данного потока.
studfiles.net
Способы задания множеств
Поиск ЛекцийТема 2: Элементы теории множеств
Каждый с самого рождения бессознательно пользуется теорией множеств, так же как Мольеров Журден из «Мещанина во дворянстве» разговаривает прозой, сам того не ведая.
М. Стоун
Основные понятия теории множеств
В конце XIX века в математической науке возникла необходимость уточнить смысл таких ведущих понятий, как функция, непрерывность и т. д. Для этого нужно было строго определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей, поэтому в конце XIX начале XX столетий происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 – 1918). За небольшой срок теория множеств стала фундаментом всей математики.
Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в многообразный мир окружающих его объектов и явлений. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие и т. п.), объединяя тем самым объекты в некоторые совокупности.
В математике понятие множествоиспользуется для описания предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.
Создатель теории множеств Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью», а так же «множество есть многое мыслимое нами как единое». Эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует. Понятие множества относится к исходным (не определяемым), на основании которых строятся остальные понятия математики.
Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой и т. д. Объекты, входящие в данное множество называются элементами множества. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств.
Множества обычно обозначаются большими буквами A, B, X, а их элементы – малыми буквами а, b, x.
Множество называется конечным, если количество его элементов можно выразить целым неотрицательным числом (причем неважно, известно это число или нет, главное, оно существует), в противном случае множество называется бесконечным.
Пример 1: Множество книг в библиотеке, множество студентов в группе являются конечными. Множество натуральных чисел, множество точек прямой являются бесконечными.
Количество элементов множества обозначается |A|.
Пример 2: Пусть В – множество правильных многоугольников. Тогда В = {тетраэдр, куб, октаэдр, додекаэдр, икосаэдр}. |B| = 5.
Запись x Х, означает что объект х есть элемент множества Х, читается «х принадлежит множеству Х», «х входит в множество Х». Если х не принадлежит множеству Х, то пишут х Х.
Например, если через Nобозначим множество натуральных чисел, то 3 N,20 N,0 N, N.
Если все элементы множества А принадлежат какому-то множеству В, то говорят, что множество А является подмножеством множества В. Записывают А В (множество А содержится во множестве В). Любое множество является подмножеством самого себя, т. е. справедливо утверждение А А.
Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом Ø. Пустое множество является подмножеством любого множества.
Подмножества, которые содержат не все элементы множества В, называют собственными подмножествами множества В.
Пример 3: Дано множество М = {a; c; m}. Найти все его подмножества.
Решение:
M1 = {a}, M2 = {c}, M3 = {m}, M4 = {a; c}, M5 = {a; m}, M6 = {c; m}, M7 = {a; c; m}, M8 = Ø.
Множества M7 и M8 называются несобственными подмножествами множества М.
Множества А и В называют равными (А = В), если. они состоят из одних и тех же элементов,т.е. В А и А В.
Например, множества А = {3, 5, 7, 9} и В = {7, 3, 9, 5} равны, т. к. состоят из одинаковых элементов.
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
Ν={1; 2; 3; …; n; …} – множество натуральных чисел – множество чисел, использующихся при счете предметов;
Ζ0={0; 1; 2; …; n; …} – множество целых неотрицательных чисел – множество натуральных чисел с нулем;
Ζ={0; ±1; ±2; …; ±n; …} – множество целых чисел – множество целых неотрицательных чисели им противоположных;
Q={ : m Z, n N} – множество рациональных чисел – множество чисел, которые можно представить в виде обыкновенной дроби – множество конечных и бесконечных периодических десятичных дробей;
R – множество действительных чисел – объединение множеств рациональных и иррациональных чисел.
Между этими множествами существует соотношение: .
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ½=0,5 (=0,5000…), ⅓=0,333… – рациональные числа.
Действительные числа, не являющиеся рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Например, = 1,4142356…, π = 3,1415926… – иррациональные числа.
Способы задания множеств
Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?
Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5, и 6, то мы задали это множество, поскольку все его элементы окажутся перечисленными. При этом возможна запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {3, 4, 5, 6}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества: указывают характеристическое свойство его элементов.
Характеристическое свойство– это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Рассмотрим, например, множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, – «быть двузначным числом». Это характеристическое свойство дает возможность решать вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так, число 45 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит, так как оно не является двузначным.
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными соседними сторонами и как множество ромбов с прямым углом.
В тех случаях, когда характеристическое свойство элементов множества можно представить в символической форме, возможна соответствующая запись множества. Например, множество А натуральных чисел, меньших 7, можно задать так: А = {х| х Nи х < 7}. При такой записи буквой х обозначается элемент множества А. для этих целей можно использовать и другие буквы латинского алфавита.
Пример 5: Даны множества: М = {2; 3; 5; 7}, N = {-5; -4; -3; -2}, F = {x| x Z, -6 < x < -1}, D = {x| x N, x < 10, x – простое число}. Какие множества равны между собой?
Решение: Множества F и D заданы характеристическими свойствами. Для того, чтобы сравнить их между собой и с остальными множествами, сформулируем их характеристические свойства словами, а затем зададим их перечислением элементов.
F – множество целых чисел, больших «-6» и меньших «-1». Этому свойству удовлетворяют числа -5, -4, -3, и -2. Из этих чисел состоит множество N. Значит, F = N.
D – множество натуральных чисел, которые меньше 10 и являются простыми. Этому свойству удовлетворяют числа 2, 3, 5 и 7. Из этих чисел состоит множество M. Следовательно, D = M.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
21. Понятие множества. Способы задания множеств. Чёткие и нечёткие, конечные и бесконечные множества
Имеется два существенно различных способа задания множеств. Можно либо перечислить все элементы множества, либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект. Таким образом, множество можно задать с помощью перечисления или с помощью описания.
При перечислении множества его элементы принято заключать в фигурные скобки: — множество четных чисел, — множество чисел кратных трем. Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.
С другой стороны, для задания (описания) некоторого множества , состоящего из элементов, обладающих свойством, используют запись. Читается как: «— множество элементовтаких, что». Например,и — множество натуральных чисел, меньших 7.
Примеры в лингвистики – модификаторы «слегка» «или» «очень» «самый» и т.д.
22. Отношения между множествами. Основные операции над множествами.
Операции над множествами
Сравнение множеств
Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.
Два множества называются равными, если они содержат одинаковые наборы элементов.
ТЕОРЕМА
Пустое множество Ø является подмножеством всех множеств.
Универсальное множество U содержит все множества.
Если , то В надмножество А.
ПРИМЕР
А={0, 1, 2, 3}, В={0, 1}, .
Объединением двух множеств называется множество, содержащее все элементы обоих множеств.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я},
.
Пересечением двух множеств называется множество, состоящее из общих элементов обоих множеств.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, ={К, Т, Я}.
Разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, А \ В={A}, В \ А ={О, С}.
Симметрической разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В и всех элементов множества В не содержащихся в А.
ПРИМЕР
А={К, А, Т, Я}, В={К, О, С, Т, Я}, А Δ В={A,О,С}.
Дополнением (дополнением до универсального множества) множества А называется множество, состоящее из всех элементов универсального множества не содержащихся в А.
Прямым или декартовым произведением множеств A и B, называется множество всех упорядоченных пар (a, b), где первый элемент a из множества A, а второй элемент b из множества B.
ПРИМЕР
,
Степенью множества называется декартовое произведение множества A само на себя n раз.
ПРИМЕР
, .
Свойства операций над множествами
1) Коммутативность.
2) Ассоциативность.
3) Дистрибутивность.
4) Закон поглощения.
5) Идемпотентность.
6) Инволютивность.
7) Свойство нуля.
АØ=А
АØ= Ø
8) Свойство единицы.
9) Закон де Моргана
Отношения между множествами
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие множествам А и В одновременно, то говорят, что эти множества пересекаются. Например, пусть множество А={a,b,c,d,e} и B = {b, c, d, k, l}. Элементы b, d принадлежат и множеству А, и множеству В. Значит, множества А и В имеют общие элементы, а сами множества пересекаются: АВ.
Если множества не имеют общих элементов, например, А = {1, 2, 3} и B = {4, 5},то они не пересекаются: А В.
Иногда приходится рассматривать не все множество, а только его часть. Например, не все множество натуральных чисел, а только множество простых чисел. Тогда речь идет о подмножестве. Если любой элемент множества А принадлежит так же и множеству В, то А называют подмножеством В. Записывают АВ. Знак называютзнаком включения.
Любое множество является подмножеством самого себя, т.е. АА. Пустое множество является подмножеством любого множества: ¾А. Все множества являются подмножествами одного и того же множества, называемого универсальным U.
Количество подмножеств множества, состоящего из n элементов равно . В нашем примере множество состоит из трех элементов, значит количество подмножеств равно=8.
Если множества состоят из одинаковых элементов и их количество равно, и каждый элемент множества А является элементом множества В и наоборот, то АВ и ВА и говорят, что множества А и В равны: А=В. Например, А={a, d, c, d}, B={c, b, d, а}, значит А=В. Для равных множеств порядок их элементов не является существенным.
Таким образом, между множествами возникают следующие отношения: множества могут пересекаться, не пересекаться, быть равными и включаться одно в другое.
Для наглядности употребляют изображения множеств на плоскости, которые называют диаграммами Эйлера-Венна(множества наглядно представляют в виде кругов, овалов), где штриховкой обозначают нужные области. Тогда вышеперечисленные отношения можно изобразить следующим образом.
Нередко бывает так, что рассматривают только подмножества одного и того же множества I. Такое множество I называют универсальным множеством. Так, если А – множество студентов первого курса, В – множество студенток в этом же институте, С – множество спортсменов этого же института, то в качестве универсального множества I можно взять множество студентов данного института, потому, что тогда АI, BI, CI.На диаграммах Эйлера-Венна универсальное множество часто изображается в виде прямоугольника, а его подмножества – кругами.
Различные числовые множества можно изображать на числовой прямой. Пусть а и b различные числа такие, что а<b. Тогда их запись и изображение таково:
studfiles.net
