Подобие прямоугольных треугольников | Треугольники
Подобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
1- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по острому углу)
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по острому углу).
2- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по двум катетам)
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по двум катетам).
3- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по катету и гипотенузе)
Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
— прямоугольные (∠C=90º, ∠C=90º).
Если
то
(по катету и гипотенузе).
Из подобия прямоугольных треугольников следуют соотношения между высотой, проведённой к гипотенузе, гипотенузой, катетами и проекциями катетов на гипотенузу, а также свойство биссектрисы треугольника.
www.treugolniki.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.
| ||||||||||
dpva.ru
Подобие прямоугольных треугольников
Подобие треугольников применяется для нахождения средних пропорциональных отрезков в прямоугольном треугольнике, через свойство биссектрисы угла.
Признаки подобия прямоугольных треугольников:
- По острым углом. Если прямоугольные треугольники имеют по равному острому углу, то такие треугольники подобны. У прямоугольного треугольника один угол прямой, поэтому для сходства двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.
- За двумя пропорциональными катетами. Если катеты одного прямоугольного треугольника пропорциональны катетам второго прямоугольного треугольника, то такие треугольники подобны.
- По пропорциональными катетом и гипотенузой. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.
Обратите внимание! Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два треугольника, подобные друг другу и подобные данном треугольнике.
Соотношение в прямоугольном треугольнике:
- Биссектриса треугольника делит противоположную сторону на отрезки, соответственно пропорциональны двум другим сторонам.
- Катет прямоугольного треугольника есть среднее пропорциональное (или средним геометрическим) между гипотенузой и проекцией этого катета на гипотенузу. Есть квадрат катета прямоугольного треугольника равен произведению гипотенузы на проекцию этого катета на гипотенузу.
- Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное (средним геометрическим) между проекциями катетов на гипотенузу есть квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равна произведению проекций катетов на гипотенузу.
xn—-7sbfhivhrke5c.xn--p1ai
Признаки подобия треугольников. Подобие прямоугольных треугольников — Геометрия — Мастер-класс
Признаки подобия треугольников. Сходство прямоугольных треугольников
Подобие треугольников играет важную роль в геометрии. Она широко применяется при вычерчивании и построении моделей. Два треугольники называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны.
Обратите внимание!
При обозначении подобных треугольников следите за тем, чтобы в названиях подобных треугольников вершины соответствующих равных углов стояли на одинаковых местах.
Для того чтобы два треугольника были подобными, достаточно, чтобы их стороны или углы удовлетворяли определенные условия, высказанные в признаках подобия.
Признаки подобия треугольников:
1. Если три стороны одного треугольника пропорциональны трем сторонам второго треугольника, то такие треугольники подобные.
2. Если две стороны одного треугольника пропорциональны двум сторонам второго треугольника и углы между этими сторонами равны, то такие треугольники подобны.
3. Если два угла одного треугольника равны двум углам второго треугольника, то такие треугольники равны.
4. Если две стороны одного треугольника пропорциональны двум сторонам второго треугольника и наибольший из противоположных им углов одного треугольника равен соответствующему углу второго треугольника, то такие треугольники подобны.
Признаки подобия прямоугольных треугольников:
За острым углом. Если прямоугольные треугольники имеют по равному острому углу, то такие треугольники подобны. У прямоугольного треугольника один угол прямой, поэтому для подобия двух прямоугольных треугольников достаточно, чтобы у них было по ровно остром углу.
За двумя пропорциональными катетами. Если катеты одного прямоугольного треугольника пропорциональные катетам второго прямоугольного треугольника, то такие треугольники подобные.
По пропорциональным катетом и гипотенузой. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.
Обратите внимание!
na-uroke.in.ua
Признаки подобия треугольников, подобие прямоугольных треугольников.
№ 345 -347 работа по учебнику
Дан четырехугольник, по рисунку необходимо сформулировать задачу. Найти:  BAD.
BAD.
Сформулируйте задачу.
— Назовите, что дано. Что требуется найти.
— Начертите рисунок в тетрадь и запишите, что дано, что требуется найти.
Дано: ABCD – четырехугольник,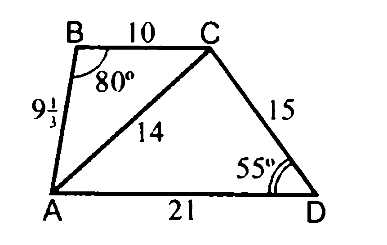
АС – диагональ,
ВС = 10, СD = 15, AD = 21, AC = 14, АВ = 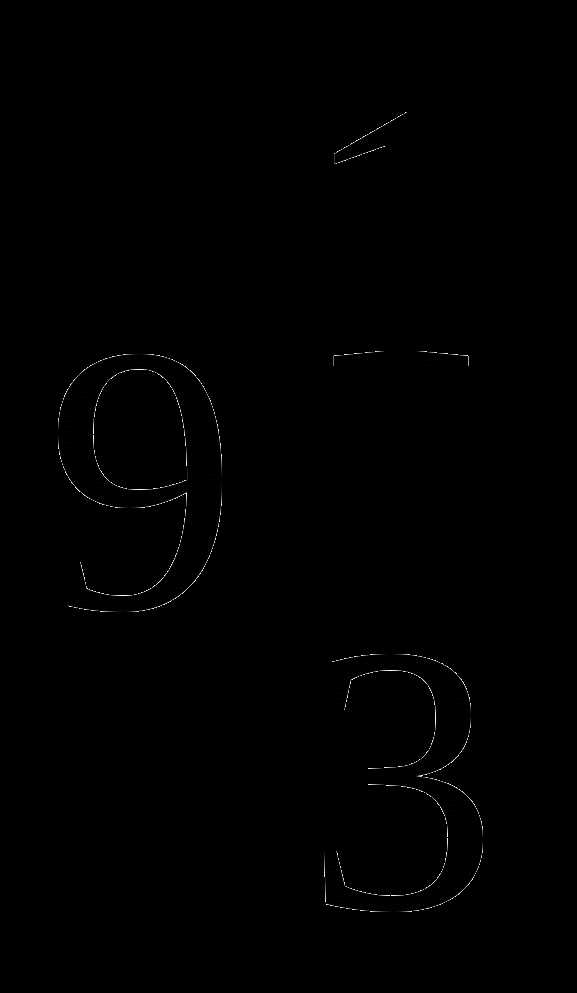 ,
,
 В = 80º,
В = 80º,  D = 55º.
D = 55º.
Найти:  BAD.
BAD.
— Прочитайте, что у вас получилось.
Поиск решения задачи:
— Что нам надо найти?  BAD
BAD
— Что достаточно знать, чтобы
найти этот угол?  ВАС
ВАС  САD
САD
— Откуда мы найдем эти углы? ∆ АВС ∆ ACD
— Если в треугольнике мы знаем один угол, что поможет нам найти другие углы? Для чего даны стороны? (устанавливаем отношение между сторонами, покажем, что треугольники подобны)

— Чему равен коэффициент подобия? 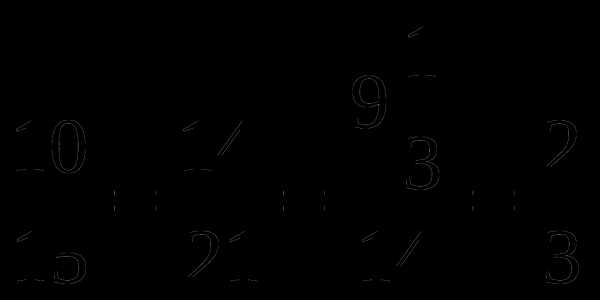
— Что из этого следует? ∆ АВС подобен ∆ ACD
— По какому признаку? (по 3 признаку)
— Что следует из подобия? равенство углов
— Какие углы сможем найти?  ВАС
ВАС  САD
САD
— А зная их, найдем…  BAD
BAD
— План решения понятен? Повторите.
План решения задачи:
— устанавливаем подобие треугольников ∆ АВС и ∆ ACD;
— доказательство подобия, через соотношение сторон;
— устанавливаем равенство соответствующих углов в подобных треугольниках;
— по свойству суммы углов треугольника находим углы  ВАС и
ВАС и  САD;
САD;
— находим угол  BAD.
BAD.
multiurok.ru
Признаки подобия прямоугольных треугольников. Пропорциональные отрезки в прямоугольном треугольнике — ГЕОМЕТРИЯ — Уроки для 8 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 32
Тема. Признаки подобия прямоугольных треугольников. Пропорциональные отрезки в прямоугольном треугольнике
Цель: сформулировать признак подобия прямоугольных треугольников с острым углом, на основе которой доказать метрические соотношения в прямоугольном треугольнике. Добиться усвоения учащимися содержания признаки подобия прямоугольных треугольников и метрических соотношений в прямоугольном треугольнике га их доведения.
Сформировать первичные умения воспроизводить изученные утверждение, записывать метрические соотношения между отрезками прямоугольного треугольника по условию задачи, а также выполнять вычисления неизвестных отрезков прямоугольного треугольника, используя записи соответствующих метрических соотношений.
Тип урока: усвоение умений и навыков.
Наглядность и оборудование: конспект «Подобие прямоугольных треугольников».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Правильность выполнения задач домашней работы проверяется во время устной фронтальной работы с рисунками к задачам, выполненными на доске заранее.
III. Формулировка цели и задач урока
Учитель напоминает ученикам о том, что в геометрии выделяют различные виды треугольников (по сторонами или углами). Поскольку в последнее время на уроках были изучены общие определения и признаки подобия треугольников, то возникает вопрос о возможной трансформации изученных утверждений для отдельных видов треугольников (кстати, некоторые из этих случаев было уже рассмотреть — см. признаки подобия равносторонних и равнобедренных треугольников).
Среди всех видов треугольников (по углам) выделяются треугольники, о которых можно сказать, что:
· один из углов всегда равна сумме двух других;
· они не могут быть равносторонними, но могут быть равнобедренного;
· для того чтобы определить остальных углов этого треугольника, достаточно знать только один из его меньших углов.
(Понятно, что речь идет о прямоугольные треугольники.)
Итак, цель урока — формулировка признаки подобия прямоугольных треугольника и исследование сферы ее практического применения.
IV. Актуализация опорных знаний
С целью успешного усвоения учащимися признаки подобия прямоугольных треугольников, метрические соотношения в прямоугольном треугольнике, а также их доведения, ученикам следует активизировать такие знания и умения: признак подобия треугольников по двум углам; определение прямоугольного треугольника и свойства острых углов прямоугольного треугольника; применение понятия о перпендикуляр к прямой, наклонная и проекция наклонной на данную прямую; основные свойства пропорции.
Выполнение устных упражнений
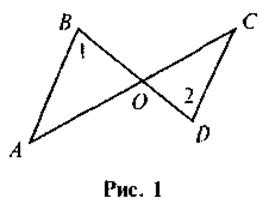
1. Докажите, что ΔАВО ~ ΔDCO , если 1 = 2 (рис. 1).
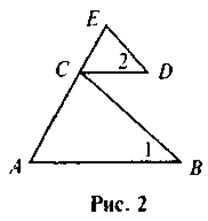
2. Докажите, что ΔАВС ~ ΔCDE , если AB || CD, 1 = 2 (рис. 2).
3. В каждом из приведенных случаев вычислите меру угла х (рис. 3).
4. Сделайте рисунок, на котором один и тот же отрезок был бы одновременно и перпендикуляром и наклонной.
5. Если 7а = 9b, то = ?
V. Усвоение знаний
План изучения нового материала
1. Признак подобия прямоугольных треугольников (с острым углом).
2. Представление о содержании понятия среднее пропорциональное число между двумя числами.
3. Теорема (метрические соотношения в прямоугольном треугольнике): формулировка и доказательство.
@ Признаки подобия прямоугольных треугольников, а также метрические соотношения в прямоугольном треугольнике, непосредственно вытекающим из признаки подобия прямоугольных треугольников с острым углом, традиционно изучаются в теме «Подобие треугольников» (в некоторых пособиях метрические соотношения называют средние пропорциональные отрезки в прямоугольном треугольнике). Содержание соответствующего параграфа нового учебника почти полностью повторяет содержание соответствующих разделов традиционного учебника геометрии. Поэтому изучение материала урока проводится по традиционной схеме.
Схема
Доказательства признаков подобия прямоугольных треугольников с острым углом |
Доведение сходства любого прямоугольного треугольника и прямоугольных треугольников, эту образуются, если в данном треугольнике провести высоту до гипотенузы |
Запись равенств отношений соответствующих сторон подобных прямоугольных треугольников v виде пропорции |
Использование полученных пропорции, основного свойства пропорции |
Некоторые изменения, внесенные авторами нового учебника к содержанию материала относительно подобия прямоугольных треугольников, является дополнительной информацией.
Так, дополнительно авторы учебника предлагают изучить:
Признаки подобия прямоугольных треугольников по двум катетами и гипотенузой и катетом.
1. Сформулируйте и докажите признак подобия прямоугольных треугольников с двумя катетами.
2. Сформулируйте и докажите признак подобия прямоугольных треугольников с гипотенузой и катетом.
Содержание понятие о среднее пропорциональное число между двумя данными числами (для лучшего понимания учениками содержания теоремы, а потому для лучшего запоминания формулировки теоремы).
А сами метрические соотношения в прямоугольном треугольнике авторы учебника записали в виде теоремы (ранее эти соотношения рассматривали как некоторые соотношения в прямоугольном треугольнике). Изменение статуса этих утверждений, без изменения их содержания, имеет чисто психологическое значение — знание формулировки теоремы и умение ее применять является обязательной программной требованием.
Материала, представленного в учебнике, автор пособия предлагает добавить один из полезных следствий из метрических соотношений, а именно: если а, b — катеты прямоугольного треугольника, с — его гипотенуза, a hc — высота, проведенная к гипотенузы, то . (Доведение с этого следствия можно провести как решение соответствующей дополнительной задачи.)
Поскольку учебный материал не является сложным, то предлагаем учащимся самостоятельную работу по его изучению (по учебнику).
Конспект 12 |
||
Подобие прямоугольных треугольников |
||
Признаки |
||
Метрические соотношения |
||
а2 = с · ас, b2 = c · bc, Последствия из метрических соотношений: |
||
1) ; |
2) |
|
V. Формирование первичных умений
Понимание признаки подобия прямоугольных треугольников с острым углом достигается во время выполнения задания. Подобны ли два прямоугольных треугольника, если:
а) они имеют общий угол;
б) они имеют общий острый угол;
в) один из них имеет угол 20°, а другой — угол 70°;
г) один из них имеет угол 50°, а катет второго вдвое меньше гипотенузы?
Формирование первичных умений применять изученную признак происходит на этапе решения учащимися упражнений.
Выполнение устных упражнений
1. На рис. 4 найдите пары подобных треугольников. Свои соображения обоснуйте. Запишите пропорциональность соответствующих сторон.
2. На рисунке 5 найдите подобные треугольники и докажите их подобие.
На применение подобия прямоугольных треугольников учащиеся решают письменные упражнения.
Выполнение письменных упражнений
Наблюдатель, находящийся в точке А, видит конец шеста В и верхнюю точку башни D, причем точки А, В и D расположены на одной прямой (рис. 6). Определите высоту башни, если ВС= 4 м, АС = 6 м, АЕ = 90 м.
VI. Формирование навыков и умений
Формированию умений записывать и использовать метрические соотношения будет способствовать выполнение устных упражнений.
Выполнение устных упражнений
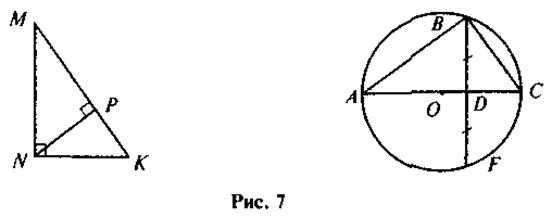
Запишите метрические соотношения для изображенных на рис. 7 прямоугольных треугольников:
Выполнение письменных упражнений
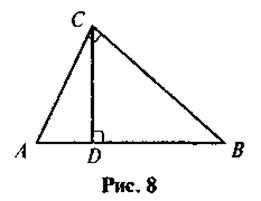
1. В прямоугольном треугольнике ABC (C = 90°) проведена высоту CD (рис. 8). Найдите:
а) CD, если AD = 4 см, DB = 25 см;
б) АС и ВС, если АВ = 50 см, AD = 18см.
2. Докажите, что проекции катетов на гипотенузу прямоугольного треугольника относятся как квадраты катетов: .
@ При доказательстве подобия треугольников требуем от учеников выполнения соображений по изученной на предыдущих уроках схеме с поправкой на содержание признаки. (Рассмотрим треугольники… и … У них углы… и… — прямые, углы… и… — равны, следовательно, треугольники… и… подобные по острым углом).
Решая задачи на применение метрических соотношений в прямоугольном треугольнике, следует требовать от учеников сначала воспроизведения словесного формулирования, а уже потом — исполнение соответствующих им символических записей.
VII. Итоги урока
Правильные записи сделаны в соответствии с рис. 9? Если нет, исправьте ошибку.
1) АМ + ВМ = АВ;
2) ВС2 = МВ · МА;
3) CM = AM · MB;
4) ;
5) АС2 = АМ · АВ.
VIII. Домашнее задание
Изучить содержание и доказательства признаков подобия прямоугольных треугольников.
Решить задачи.
1. Для построения четвертого пропорционального отрезка х = ученик предложил построить прямоугольный треугольник с катетами а и b и гипотенузой с и провести в нем высоту hc, которая будет равняться х. Второй ученик утверждает, что этот способ неправильный. Кто из учеников прав?
2. На рисунке 10 найдите подобные треугольники и докажите их подобие.
3. Высота дерева равна 9,2 м, а длина тени человека, рост которого 1,8 м, равна 2,7 м. Найдите длину тени дерева.
4. Найдите периметр прямоугольного треугольника, высота которого делит гипотенузу на отрезки длиной 4,5 см и 8 см.
na-uroke.in.ua
Признаки подобия треугольников — это… Что такое Признаки подобия треугольников?
- Признаки подобия треугольников
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.
Признаки подобия треугольников
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Первый признак
Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, ∠B=∠B1.Доказать: ∆ABC ∆A1B1C1.
Доказательство
Второй признак
Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
Дано: ∆ABC и ∆A1B1C1, ∠A=∠A1, = .Доказать: ∆ABC ∆A1B1C1.
Доказательство
Третий признак
Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.
Дано: ∆ABC и ∆A1B1C1, = = .Доказать: ∆ABC ∆A1B1C1.
Доказательство
Признаки подобия прямоугольных треугольников
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. второй признак.
Свойства подобных треугольников
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
Связанные определения
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
Литература
- Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
См. также
Ссылки
Wikimedia Foundation. 2010.
- Признак Абеля
- Признание: Два лица зла (фильм)
Смотреть что такое «Признаки подобия треугольников» в других словарях:
Признаки равенства треугольников — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
Подобие треугольников — Признаки подобия треугольников геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов. Содержание 1 Признаки подобия треугольников 1.1 Первый признак … Википедия
Преобразование подобия — Подобие преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны … Википедия
Подобные треугольники — Подобные треугольники треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак … Википедия
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где положительное число, называемое… … Википедия
Подобные фигуры — Подобие преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны … Википедия
подобие — я; ср. 1. Пренебр. Нечто похожее, сходное с чем л. Жалкое п. старинного полонеза. П. человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на себя). 2. Матем … Энциклопедический словарь
Площадь треугольника — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
подобие — я; ср. 1) пренебр. Нечто похожее, сходное с чем л. Жалкое подо/бие старинного полонеза. Подо/бие человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на… … Словарь многих выражений
dik.academic.ru


