Производная корня
См. также:
Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке.
Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени — это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби.
Пояснение:
( √x )’ = ( х1/2 )’
Квадратный корень — это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
Производная кубического корня (производная корня третьей степени)
Производная кубического корня находится точно по такому же принципу, что и квадратного.Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.
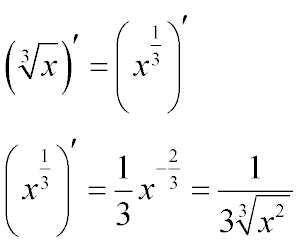
Степень -2/3 получается в следствие вычитания единицы из 1/3
Производная переменной под корнем произвольной степени
Данная формула пригодна для нахождения производной корня любой степени:( n√x )’ = 1 / ( n n√xn-1 )
В более удобном для глаза виде она представлена на картинке выше.Здесь:
n — степень корня, для которой находится производная
x — переменная, для которой находится производная
profmeter.com.ua
производная корня | математика-повторение
На этом занятии мы будем учиться применять формулы и правила дифференцирования.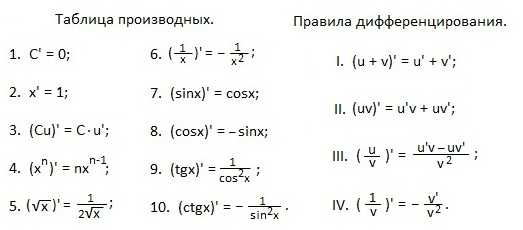
Примеры. Найти производные функций.
1. y=x7+x5-x4+x3-x2+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:
y’=7x6+5x4-4x3+3x2-2x+1.
2. y=3x6-2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x5-2=18x5-2.
Применяем правило I, формулы 3, 5 и 6 и 1.
Применяем правило IV, формулы 5 и 1.
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример
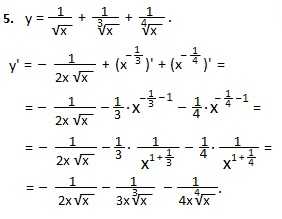 Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4. Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
www.mathematics-repetition.com
Производная степенной функции (степени и корни)
Производная от x в степени a равна a, умноженному на x в степени a минус один:
(1) .
Производная от корня степени n из x в степени m равна:
(2) .
Вывод формулы производной степенной функции
Случай x > 0
Рассмотрим степенную функцию от переменной x с показателем степени a:
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .
Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.
Теперь находим производную, применяя правило дифференцирования сложной функции:
;
.
Здесь .
Формула (1) доказана.
Вывод формулы производной от корня степени n из x в степени m
Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .
Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.
По формуле (1) находим производную:
(1) ;
;
(2) .
На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).
Случай x = 0
Если , то степенная функция определена и при значении переменной x = 0. Найдем производную функции (3) при x = 0. Для этого воспользуемся определением производной:
.
Подставим x = 0:
.
При этом под производной мы понимаем правосторонний предел, для которого .
Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0.
Случай x < 0
Снова рассмотрим функцию (3):
(3) .
При некоторых значениях постоянной a, она определена и при отрицательных значениях переменной x. А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.
Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x. Например, при n = 3 и m = 1 мы имеем кубический корень из x:
.
Он определен и при отрицательных значениях переменной x.
Найдем производную степенной функции (3) при и при рациональных значениях постоянной a, для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:
.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .
Производные высших порядков
Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.
Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;
.
Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.
Заметим, что если a является натуральным числом, , то n-я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .
Примеры вычисления производных
Пример
Найдите производную функции:
.
Решение
Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.
Находим производные степеней:
;
.
Производная постоянной равна нулю:
.
Применяем правило дифференцирования суммы и выносим постоянные за знак производной:
.
Применяем правило дифференцирования сложной функции:
.
Здесь .
Преобразуем степени в корни:
;
;
;
;
;
.
Ответ
Еще примеры
Найти производные следующих функций, зависящих от переменной x:
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >
Найти производную шестого порядка следующей функции:
.
Решение > > >
Все примеры > > >
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Производная корня икс — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ
Производная корня икс равна единице, деленной на два таких же корня.
Данную формулу можно получить из формулы производной степенной функции , представив корень в виде дробного показателя:
Примеры решения задач по теме «Производная корня»
ПРИМЕР 1
Найти производную функции
Искомая производная
По правилам дифференцирования производная суммы равна сумме производных. То есть тогда
Производная первого слагаемого, как константы, равна 0:
Найдем производную второго слагаемого
Вначале по правилу дифференцирования вынесем константу за знак производной:
Далее находим производную от корня по формуле . И так как подкоренное выражение есть сложная функция (оно отлично от просто x), то еще дробь нужно будет умножить на производную от подкоренного выражения:
Производная от суммы равна сумме производных:
Первая производная от независимой переменной равна единице, а производная от константы 2 равна нулю, то есть имеем:
Итак,Ответ
ПРИМЕР 2
Производная от корня равна единице деленной на два таких же корня. Но так как подкоренное выражение является сложной функцией (под корнем стоит не просто x, а sin x ), то еще надо домножить на производную от подкоренного выражения, то есть синуса. Производная от синуса равна косинусу . Тогда имеем:
Ответ
sciterm.ru
Как найти производную корня
В задачах по математическому анализу иногда требуется найти производную корня. В зависимости от условий задачи, производная от функции «корень квадратный» (кубический) находится непосредственно или путем преобразования «корня» в степенную функцию с дробным показателем.Вам понадобится
- — карандаш;
- — бумага.
Инструкция
- Перед тем как находить производную корня, обратите внимание на остальные функции, присутствующие в решаемом примере. Если в задаче имеется много подкоренных выражений, то воспользуйтесь следующим правилом нахождения производной квадратного корня:(√х)’ = 1 / 2√х.
- А для нахождения производной кубического корня примените формулу:(³√х)’ = 1 / 3(³√х)²,где через ³√х обозначен кубический корень из х.
- Если в примере, предназначенном для дифференцирования, встречается переменная в дробных степенях, то переведите обозначение корня в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓:√х = х ^ ½,³√х = x ^ ⅓,где символ ^ обозначает возведение в степень.
- Для нахождения производной степенной функции вообще и х^½, x^⅓, в частности, воспользуйтесь следующим правилом:(х ^ n)’ = n * x^(n-1).Для производной корня из этого соотношения вытекает:(х^½)’ = ½ x ^ (-½) и
(x^⅓)’ = ⅓ x ^ (-⅔). - Продифференцировав все корни, внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.
- Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
• производная константы (постоянного числа, C) равняется нулю: C’ = 0;
• постоянный множитель выносится за знак производной: (k*f)’ = k * (f)’ (f – произвольная функция) ;
• производная суммы нескольких функций равняется сумме производных: (f + g)’ = (f)’ + (g)’;
• производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)’ = (f)’g + f (g)’;
• производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)’ = ((f)’g – f(g)’) / g².
completerepair.ru
Решение квадратных уравнений через производные / Habr
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль». Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
habr.com
