Производная синус 2 х – Производная sin 2x

Найти производную y’ = f'(x) = 2^sin(x^2) (2 в степени синус от (х в квадрате))

Решение

$$2^{\sin{\left (x^{2} \right )}}$$

Подробное решение

[LaTeX]

1. Заменим .

3. Затем примените цепочку правил. Умножим на :

   1. Заменим .

   2. Производная синуса есть косинус:

4. Затем примените цепочку правил. Умножим на :

   1. В силу правила, применим: получим

   В результате последовательности правил:

В результате последовательности правил:

Теперь упростим:

---

Ответ:

Первая производная

[LaTeX]

        / 2\               
     sin\x /    / 2\       
2*x*2       *cos\x /*log(2)

$$2 \cdot 2^{\sin{\left (x^{2} \right )}} x \log{\left (2 \right )} \cos{\left (x^{2} \right )}$$

Вторая производная

[LaTeX]

      / 2\                                                         
   sin\x / /     2    / 2\      2    2/ 2\             / 2\\       
2*2       *\- 2*x *sin\x / + 2*x *cos \x /*log(2) + cos\x //*log(2)

$$2 \cdot 2^{\sin{\left (x^{2} \right )}} \left(- 2 x^{2} \sin{\left (x^{2} \right )} + 2 x^{2} \log{\left (2 \right )} \cos^{2}{\left (x^{2} \right )} + \cos{\left (x^{2} \right )}\right) \log{\left (2 \right )}$$

Третья производная

[LaTeX]

        / 2\                                                                                                              
     sin\x / /       / 2\      2    / 2\        2/ 2\             2    3/ 2\    2         2    / 2\           / 2\\       
4*x*2       *\- 3*sin\x / - 2*x *cos\x / + 3*cos \x /*log(2) + 2*x *cos \x /*log (2) - 6*x *cos\x /*log(2)*sin\x //*log(2)

$$4 \cdot 2^{\sin{\left (x^{2} \right )}} x \left(- 6 x^{2} \log{\left (2 \right )} \sin{\left (x^{2} \right )} \cos{\left (x^{2} \right )} + 2 x^{2} \log^{2}{\left (2 \right )} \cos^{3}{\left (x^{2} \right )} — 2 x^{2} \cos{\left (x^{2} \right )} — 3 \sin{\left (x^{2} \right )} + 3 \log{\left (2 \right )} \cos^{2}{\left (x^{2} \right )}\right) \log{\left (2 \right )}$$

www.kontrolnaya-rabota.ru

Найти производную y’ = f'(x) = (sin((x+h)/2))/(sin(x/2)) ((синус от ((х плюс h) делить на 2)) делить на (синус от (х делить на 2)))

Решение

   /x + h\
sin|-----|
   \  2  /
----------
     /x\  
  sin|-|  
     \2/  

$$\frac{\sin{\left (\frac{1}{2} \left(h + x\right) \right )}}{\sin{\left (\frac{x}{2} \right )}}$$

Подробное решение

[LaTeX]

1. Применим правило производной частного:

   и .

   Чтобы найти :

   1. Заменим .

   2. Производная синуса есть косинус:

2. Затем примените цепочку правил. Умножим на :

   1. Производная произведения константы на функцию есть произведение этой константы на производную данной функции.

      1. дифференцируем почленно:

         1. В силу правила, применим: получим

         2. Производная постоянной равна нулю.

         В результате:

      Таким образом, в результате:

   В результате последовательности правил:

Чтобы найти :

1. Заменим .

2. Производная синуса есть косинус:

3. Затем примените цепочку правил. Умножим на :

   1. Производная произведения константы на функцию есть произведение этой константы на производную данной функции.

      1. В силу правила, применим: получим

      Таким образом, в результате:

   В результате последовательности правил:

Теперь применим правило производной деления:

Теперь упростим:

---

Ответ:

Первая производная

[LaTeX]

   /x + h\      /x\    /x + h\
cos|-----|   cos|-|*sin|-----|
   \  2  /      \2/    \  2  /
---------- - -----------------
      /x\             2/x\    
 2*sin|-|        2*sin |-|    
      \2/              \2/    

$$\frac{\cos{\left (\frac{1}{2} \left(h + x\right) \right )}}{2 \sin{\left (\frac{x}{2} \right )}} — \frac{\cos{\left (\frac{x}{2} \right )}}{2 \sin^{2}{\left (\frac{x}{2} \right )}} \sin{\left (\frac{1}{2} \left(h + x\right) \right )}$$

Вторая производная

[LaTeX]

/                  /x\    /h + x\\       
|               cos|-|*sin|-----||       
|     /h + x\      \2/    \  2  /|    /x\
|- cos|-----| + -----------------|*cos|-|
|     \  2  /            /x\     |    \2/
|                     sin|-|     |       
\                        \2/     /       
-----------------------------------------
                     2/x\                
                2*sin |-|                
                      \2/                

$$\frac{\cos{\left (\frac{x}{2} \right )}}{2 \sin^{2}{\left (\frac{x}{2} \right )}} \left(- \cos{\left (\frac{1}{2} \left(h + x\right) \right )} + \frac{\cos{\left (\frac{x}{2} \right )}}{\sin{\left (\frac{x}{2} \right )}} \sin{\left (\frac{1}{2} \left(h + x\right) \right )}\right)$$

Третья производная

[LaTeX]

     /x\    /h + x\        3/x\    /h + x\        2/x\    /h + x\             
  cos|-|*sin|-----|   3*cos |-|*sin|-----|   3*cos |-|*cos|-----|             
     \2/    \  2  /         \2/    \  2  /         \2/    \  2  /      /h + x\
- ----------------- - -------------------- + -------------------- + cos|-----|
           /x\                 3/x\                   2/x\             \  2  /
        sin|-|              sin |-|                sin |-|                    
           \2/                  \2/                    \2/                    
------------------------------------------------------------------------------
                                        /x\                                   
                                   4*sin|-|                                   
                                        \2/                                   

$$\frac{1}{4 \sin{\left (\frac{x}{2} \right )}} \left(\cos{\left (\frac{1}{2} \left(h + x\right) \right )} — \frac{\cos{\left (\frac{x}{2} \right )}}{\sin{\left (\frac{x}{2} \right )}} \sin{\left (\frac{1}{2} \left(h + x\right) \right )} + \frac{3 \cos^{2}{\left (\frac{x}{2} \right )}}{\sin^{2}{\left (\frac{x}{2} \right )}} \cos{\left (\frac{1}{2} \left(h + x\right) \right )} — \frac{3 \cos^{3}{\left (\frac{x}{2} \right )}}{\sin^{3}{\left (\frac{x}{2} \right )}} \sin{\left (\frac{1}{2} \left(h + x\right) \right )}\right)$$

www.kontrolnaya-rabota.ru

2) Производная синуса.

При определении производной синуса удобно брать приращение аргумента не одностороннее, а двустороннее, с одинаковым интервалом h влево и вправо от исследуемой точки графика. Тогда

x = 2 · h ; y = sin (x + h) – sin (x – h) =

=(sin x·cos h + cos x·sin h) – (sin x·cos h – cos x·sin h) = 2·cos x·sin h ;

y/x = (2 · cos x · sin h) / (2 · h) = cos x · sin h / h ;

Отношение sin h / h есть первый замечательный предел, равный1при стремлении аргумента к нулю, поэтому окончательно имеем

dy/dx =cos x .

Производная синуса равна косинусу того же аргумента.

3) Производная натурального логарифма:

y = ln x;введем промежуточное обозначениеt=x/x. Тогда

y = ln (x+x) – ln x = ln ((x+x)/x) = ln (1+x/x) = ln (1+1/t),

или y/x = (1/x) · ln (1+1/t) = (t/x) · ln (1+1/t) = (1/x) · ln (1+1/t)t .

П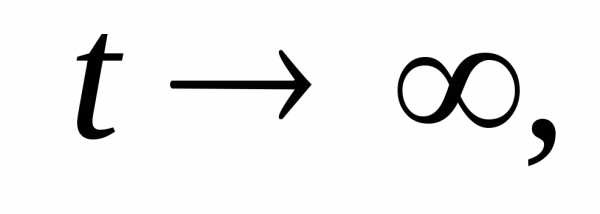

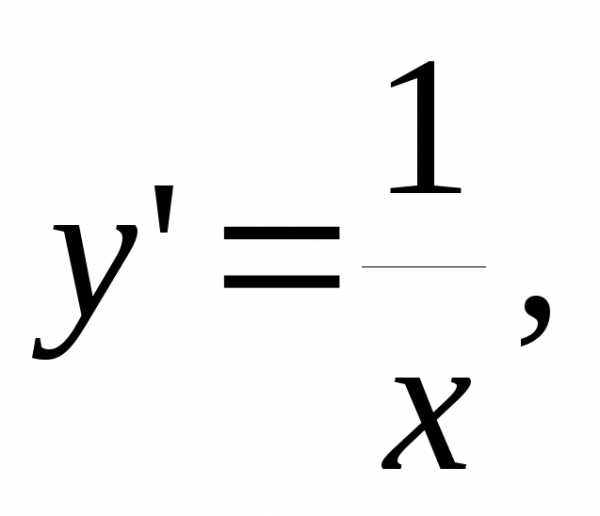
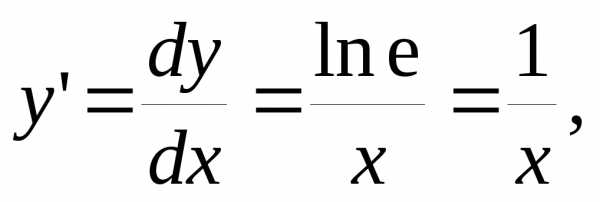ри имеем и видно, что выражение под знаком логарифма есть второй замечательный предел – числоe– основание натуральных логарифмов. По определению,ln e = 1,и тогда : или, короче,

или Производная натурального логарифма есть обратная величина аргумента.

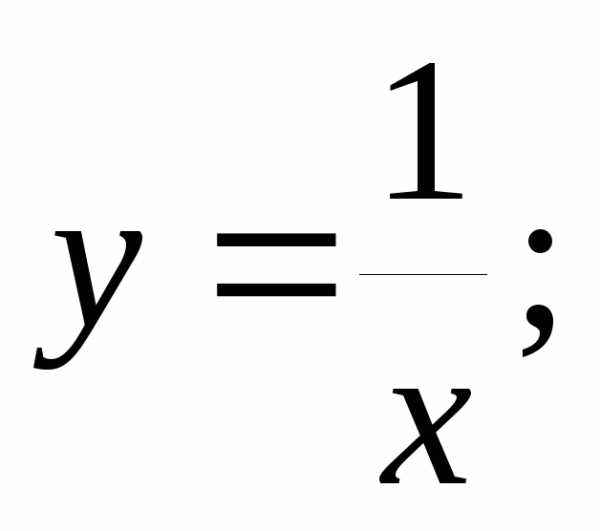
4) Производная обратной величины.

Вычисляем разность приращенного и исходного значений функции:

Делим на приращение аргумента и переходим к пределу:

Производная обратной величины равна минус обратному квадрату аргумента.

Замечание. Обратная величина есть частный случай степенной функции, так что выведение этой формулы является избыточным. Оно, однако, полезно, показывая достижимость одного и того же результата разными путями.

4.3. Функции с одноканальной зависимостью от аргумента

Мы переходим к выводу правил дифференцирования сложных функций, используя правила преобразований структурных схем (см. главу 3) и формулы для дифференцирования трех функций, принятых за основные (см. п. 4.2). На самом деле, большинство из них сложными не являются, но действия с ними выполняются по единообразным правилам для сложных функций из аппарата МСС.

Функции, рассматриваемые ниже в п. 4.3-4.5, а также и ряд других, относят к элементарным и сводят в справочные таблицы. Вопрос об отнесении их к этой категории есть вопрос практического удобства – что проще: каждый раз выводить формулу заново или иметь длинный перечень табличных формул, требующих запоминания или поиска.

Вывод формул дифференцирования с помощью МСС

производится в следующем порядке.

1. Составляем структурную схему для исходной формулы.

2. Определяем коэффициенты передачи частных связей (КПЧС) для всех стрелок схемы.

3. Свертываем схему, определяя ее результирующий коэффициент передачи (РКП) – это и есть искомая производная.

Использование этой методики выявляет не замечавшиеся раньше особенности процедуры. Так, в традиционной схеме не уделяется должного внимания числу каналов влияния аргумента на функцию. При работе с МССстановится ясно, что функции полезно классифицировать именно по этому признаку.

studfiles.net