Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Пример 1. Найти производную функции
y = cos 2x
Решение. Воcпользовавшись формулой для производной сложной функции y = cos (kx + b) в случае, когда k = 2, b = 0, получим
(cos 2x)’ = – 2sin 2x .
Замечание. Очень часто школьники, а также и студенты, при решении примера 1 пишут:
(cos 2x)’ = – sin 2x .
Это ошибка !!!
Перепишем верный ответ еще раз:
(cos 2x)’ = – 2sin 2x .
Приведем также верные ответы в похожих примерах:
Пример 2. Найти производную функции
y = sin3x
Решение. Воcпользовавшись формулой для производной сложной функции y = ( f (x)) c в случае, когда f (x) = sin x , а c = 3, получим
Ответ:
Пример 3. Найти производную функции
y = (3x – 7)5 .
Решение. Воcпользовавшись формулой для производной сложной функции y = (kx + b)c в случае, когда k = 3, b = – 7, а c = 5, получим
y’ = 15(3x – 7)4 .
Ответ:
Пример 4 . Найти производную функции
Решение. Поскольку
,
то исходную функцию можно переписать в виде
Воcпользовавшись формулой для производной сложной функции y = ( f (x)) c в случае, когда
,
а c = 8, получим

Ответ:

Пример 5 . Найти производную функции
Решение. Воcпользовавшись правилом 5 для вычисления производной частного двух функций и формулой для производной сложной функции y = arccos (kx + b) в случае, когда k = 3, b = 0, получим

Ответ:
.Пример 6. Найти производную функции
Решение. Воcпользовавшись правилом 4 для вычисления производной произведения двух функций, формулой для производной сложной функции y = arctg (kx + b) в случае, когда k = 5, b = 0, и формулой для производной сложной функции y = akx + b в случае, когда a = 3, k = 2, b = 0, получим

Ответ:
Пример 7 . Найти производную функции
Решение. Поскольку
то, воcпользовавшись формулой для производной сложной функции y = e f (x) в случае, когда , и формулой для производной сложной функции y = (kx + b)c в случае, когда с = – 1, k = 7, b = – 1, получим

Ответ:
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Производные тригонометрических функций, примеры
Теория по производным тригонометрических функций
Производные тригонометрических функций равны соответственно:
Используя эти производные и правила дифференцирования, выведем формулу для нахождения производной функции . Представим эту функции как , тогда
Далее по правилу дифференцирования частного, получим
Учитывая, что в числителе у нас записано основное тригонометрическое тождество, окончательно получим:
Аналогично можно вывести формулу для котангенса
Примеры
| Понравился сайт? Расскажи друзьям! | |||
Решение производных
Для того чтобы понять определение производной рассмотрим следующий график функции.
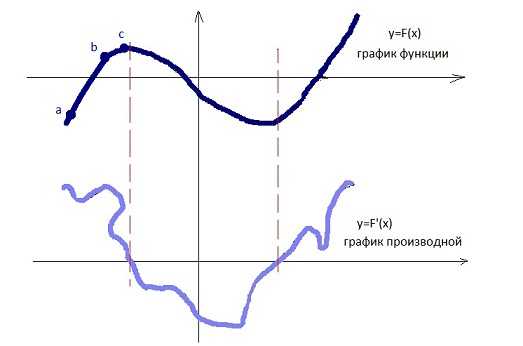
Рис.1. Пример функции и ее производной.
Глядя на рисунок можно увидеть места, где функция растет быстрее, а где убывает. Например, с точки a до точки b график поднимается стремительнее, чем с точки b до точки c.
Если перенести точки с графика функции на новую систему координат таким образом, чтобы точки возрастания располагались выше по оси x, а точки убывания ниже оси x (соблюдая масштаб) и соединить эти точки, то получится новый график новой функции (нижний график на рис. 1). Данная функция и есть производная от основной функции. Данный график есть не что иное, как показатель скорости изменения функции. Другими словами, производная – показатель скорости изменения функции. На практике производные применяются для определения скорости изменения каких-нибудь процессов: физических, химических, экономических и т.д.
Если говорить более сложным языком, то производная – это предел, к которому стремится отношение приращения x к приращению y. В общем виде производная функция выглядит и определяется следующим образом:
Процесс вычисления производной функции называется дифференцированием.
Функций на практике встречается великое множество, но есть простые функции (элементарные), такие как, F(x)=sinx, F(x)=C (где С-константа), F(x)=lnx и т.д. Для этих элементарных функций уже определены производные, и достаточно выучить их наизусть. Производные простых (элементарных) функций приведены в таблице ниже.
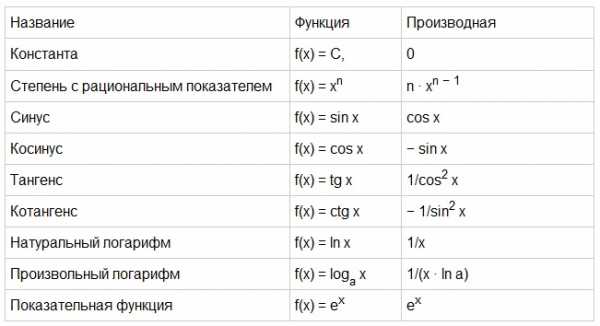
Решение производных, говоря простым языком, заключается в превращении одной функции в другую, следуя определенным правилам (исключением, является экспоненциальная функция F(x)=e^x, которая не меняется).
Рассмотрим пример. Необходимо найти производную функции F(x)=х^3 + 3x^2 — 72x + 90
Для решения производной достаточно воспользоваться таблицей производных простых (элементарных) функций. В соответствии с данными из таблицы получим производную:
F’(x)= (х^3 + 3x^2 — 72x + 90)’=3x^2+6x-72
Решение сложных производных
На практике с решением производных сложных функций приходится сталкиваться значительно чаще, чем с простыми.
Правило определения производной сложной функции выглядит следующим образом:
(a(b))’=a’(b)*b’, где a-внешняя функция, b-внутренняя функция.
Рассмотрим пример
Необходимо найти производную функции F(x)=sin(3x-5)
Найти производную данной функции, воспользовавшись таблицей простых (элементарных) функций, не получится, так как под sin находится целое выражение, т.е. функция состоит из двух функций a=sin(x)(внешняя функция) и b=3x-5 (внутренняя функция).
Воспользуемся правилом определения производной сложной функции и получим:
F’(x)=(sin(3x-5))’=cos(3x-5)*(3x-5)’=3cos(3x-5).
заметка: деревянные окна (http://www.woodlan.ru/) и Продвижение товара и услуг в интернете недорого от частного специалиста подробнее на http://seoshnig.ru.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
