Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
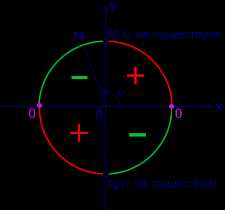
Знаки тригонометрических функций
Знаки чисел
sin α , cos α , tg α , ctg α
определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3, 4).
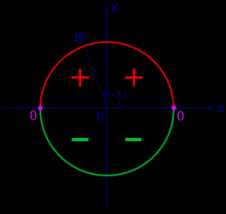 |  |
| Рис.1. Знак sin α | Рис.2. Знак cos α |
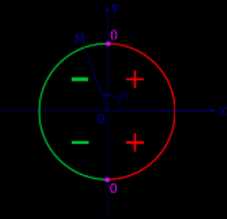
 | |
| Рис.3. Знак tg α | Рис.4. Знак ctg α |
Периодичность тригонометрических функций. Полупериодичность синуса и косинуса
Рассмотрим рисунок 5.
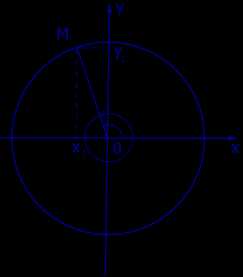
Рис.5
Если луч OM1, изображенный на рисунке 5, повернуть по ходу или против хода часов на полный угол (360 градусов или 2π радиан), то он совместится с самим собой. Следовательно, справедливы формулы:
sin (α° + 360°) = sin α°, cos (α° + 360°) = cos α°,
sin (α° – 360°) = sin α°, cos (α° – 360°) = cos α°,
а также формулы:
sin (α + 2π) = sin α , cos (α + 2π) = cos α ,
sin (α – 2π) = sin α, cos (α – 2π) = cos α .
Поворачивая луч OM1 на полный угол по ходу или против хода часов n раз ( 360n градусов или 2nπ радиан), получаем следующие формулы:
Таким образом, в случае, когда углы измеряются в градусах, периодами синуса и косинуса являются углы 360° n, .
В случае, когда углы измеряются в радианах, периодами синуса и косинуса являются числа 2nπ, .
В случае, когда углы измеряются в градусах, наименьшим положительным периодом синуса и косинуса является угол 360°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом синуса и косинуса является число 2π .
Теперь рассмотрим рисунок 6.

Рис.6
Если луч OM1, изображенный на рисунке 6, повернуть по ходу или против хода часов на развернутый угол (180 градусов или π радиан), то он совместится с лучом OM2 . Следовательно, справедливы формулы:
sin (α° + 180°) = – sin α°, cos (α° + 180°) = – cos α°,
sin (α° – 180°) = – sin α°, cos (α° – 180°) = – cos α°,
а также формулы:
sin (α + π) = – sin α , cos (α + π) = – cos α ,
sin (α – π) = – sin α, cos (α – π) = – cos α.
Полученные формулы описывают свойство полупериодичности синуса и косинуса.
Таким образом, в случае, когда углы измеряются в градусах, угол 180° является полупериодом синуса и косинуса.
В случае, когда углы измеряются в радианах, полупериодом синуса и косинуса является число π.
Следствие. Поскольку
то справедливы формулы:
Таким образом, в случае, когда углы измеряются в градусах, периодами тангенса и котангенса являются углы 180° n,
В случае, когда углы измеряются в радианах, периодами тангенса и котангенса являются числа nπ, .
В случае, когда углы измеряются в градусах, наименьшим положительным периодом тангенса и котангенса является угол 180°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом тангенса и котангенса являются число π.
Четность тригонометрических функций
Рассмотрим рисунок 7.
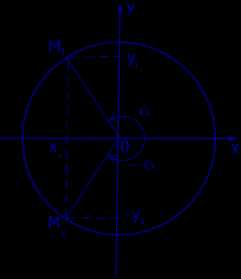
Рис.7
На этом рисунке

Следовательно, справедливы формулы:
sin ( – α ) = – sin α , cos ( – α ) = cos α ,
откуда вытекают формулы:
tg ( – α ) = – tg α , ctg ( – α ) = – ctg α .
Таким образом, косинус – четная функция, а синус, тангенс и котангенс – нечетные функции.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Свойства тригонометрических функций
III. Актуализация знаний.
Используя прием «Путешествие по галерее» переходим к новой теме. Реферат «История возникновения тригонометрии».
Что означает в переводе с греческого слово «тригонометрия». Слово «тригонон» — треугольник, а слово «метрезис» или «метрео» – измеряю, значит тригонометрия – это «измерение треугольников». Тригонометрия дает методы решения реальных задач, возникающих в физике, электротехнике, астрономии, геодезии, картографии и других науках. В своем развитии она прошла две стадии. Изначально тригонометрия возникла в античном мире и развивалась в тесной связи с астрономией. Тригонометрические знания были нужны для определения положения небесных светил, составления карты звездного неба, предсказания солнечных затмений, расчетов траекторий комет и т.п. В средневековое время она развивалась благодаря потребностям географии, геодезии, военного дела. Тригонометрия приобрела современный вид, наиболее удобный для решения задач в 18 веке в трудах Леонардо Эйлера. Эйлер внёс огромный вклад в изучении свойств тригонометрических функции.
И на этом тема нашего урока «Свойства тригонометрических функции».
Постановка цели урока (изучить тему, научиться использовать свойства при решении задач).
Из определения тригометрических функции следует, что знаки «+» и «-» каждой функции зависят от того в какой координатной четверти лежит его конец.
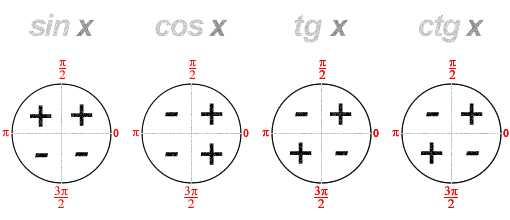
Знаки тригонометрических функции можно указать также в виде таблицы.
Например:
1. Определите знак tg, если tgα0, cosα
2. Определите знак произведения:
А) (положительный)
Б) (отрицательный)
Так как значение тригонометрических функции принимают те же значения и при полном обороте, они называются периодическими функциями. Отсюда при нахождении значений угла больше 3600 применяем данные формулы.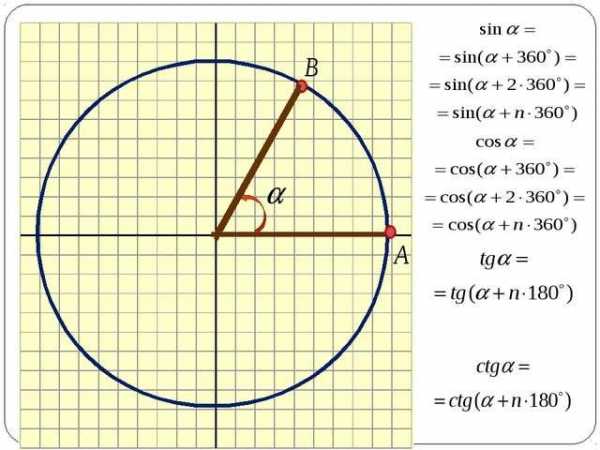
Например:
Вычислите: cos4200=
До сих пор мы рассматривали тригонометрические функции, где . Теперь перейдём к рассмотрению формулы, которая выражает тригонометрические функций отрицательного аргумента через значения тригонометрических функций с положительным аргументом. Для этого в прямоугольной координатной системе, возьмём окружность с центром в начале координат и с радиусом ОР.
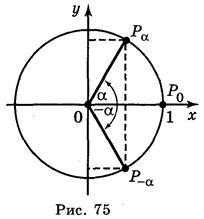
Если радиус повернёт против часовой стрелки, он займёт положение ОРα, если по часовой стрелке, то займёт положение ОР-α.
Здесь одинаковые абсциссы и противоположные ординаты. Отсюда, если координаты ОРα(х;у), то координаты точки ОР-α(х;-у). Значит
Запишем это в виде формулы следующим образом:
Определение:
Если изменение знака аргумента влечёт за собой и изменение знака функции, то функция называется нечетной, а если знак не изменился, то функция называется четной. Следовательно: синус, тангенс, котангенс являются нечетными функциями. Косинус является четной функцией.
Например:
Найдите значения выражений:
Cos(-π)+2sin(-π/6)=
compedu.ru
Тригонометрические функции, их свойства и графики.
Количество просмотров публикации Тригонометрические функции, их свойства и графики. — 1838
Функция синус y = sin(x).
Изобразим график функции синус, его называют «синусоида».
Свойства функции синус y = sinx:
- Областью определения: .
- Область значений:
- Наименьший положительный период функции синуса равен .
- Функция обращается в ноль при , где , Z – множество целых чисел.
- Функция синус — нечетная.
- Функция убывает при , возрастает при .
- Функция синус имеет локальные максимумы в точках , локальные минимумы в точках .
- Функция y = sinx вогнутая при , выпуклая при .
- Координаты точек перегиба .
- Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют «косинусоида») имеет вид:
Свойства функции косинус
1.Область определения функции косинус: .
2.Область значений: .
3.Наименьший положительный период функции косинус равен .
4.Функция обращается в ноль при , где , Z – множество целых чисел.
5.Функция косинус — четная.
6.Функция убывает при , возрастает при .
7.Функция y = cosx имеет локальные максимумы в точках , локальные минимумы в точках .
8.Функция вогнутая при , выпуклая при .
9.Координаты точек перегиба .
10.Асимптот нет.
Функция тангенс y = tg(x).
График функции тангенс (его называют «тангенсоида») имеет вид:
Свойства функции тангенс y = tgx:
1.Область определения функции тангенс: , где , Z – множество целых чисел.
2.Область значений функции тангенс: .
3.Наименьший положительный период функции тангенс равен .
4.Функция обращается в ноль при , где , Z – множество целых чисел.
5.Функция тангенс — нечетная.
6.Функция возрастает при .
7.Функция вогнутая при ,
выпуклая при .
8.Координаты точек перегиба .
9.Наклонных и горизонтальных асимптот нет.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют «котангенсоида»):
Свойства функции котангенс y = ctgx:
1.Область определения: , где , Z – множество целых чисел.
2.Область значений: .
3.Наименьший положительный период функции котангенс равен .
4.Функция обращается в ноль при , где , Z – множество целых чисел.
5.Функция нечетная.
6.Функция котангенс убывает при .
7.Функция котангенс вогнутая при , выпуклая при .
8.Координаты точек перегиба .
9.Наклонных и горизонтальных асимптот нет.
referatwork.ru
Свойства тригонометрических функций: гармонические колебания
Рассмотрим свойства тригонометрических функций, их особенности и отличия друг от друга.
Функция sin(x)
1. Область определения: R
2. Область значений: [-1;1]
3. Нечетная.
4. Наименьший положительный период: 2*pi
5. Координаты точек пересечения графика функции с осью Ох: (pi*n; 0)
6. Координаты точек пересечения графика функции с осью Оу: (0;0)
7. Промежутки, на которых функция положительна: (2*pi*n; pi+2*pi*n)
8. Промежутки, на которых функция отрицательна: (-pi + 2*pi*n; 2*pi*n)
9. Промежутки возрастания: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
10. Промежутки убывания: [pi/2 +2*pi*n; 3*pi/2 +2*pi*n]
11. Точки минимума: -pi/2 +2*pi*n
12. Минимумы функции: -1
13. Точки максимума: pi/2 +2*pi*n
14. Максимумы функции: 1
Функция cos(x)
1. Область определения: R
2. Область значений: [-1;1]
3. Четная
4. Наименьший положительный период: 2*pi
5. Координаты точек пересечения графика функции с осью Ох: (pi/2 +pi*n; 0)
6. Координаты точек пересечения графика функции с осью Оу: (0;1)
7. Промежутки, на которых функция положительна: (-pi/2 +2*pi*n; pi/2 +2*pi*n)
8. Промежутки, на которых функция отрицательна: (pi/2 +2*pi*n; 3*pi/2 +2*pi*n)
9. Промежутки возрастания: [-pi + 2*pi*n; 2*pi*n]
10. Промежутки убывания: [2*pi*n; pi+2*pi*n]
11. Точки минимума: pi+2*pi*n
12. Минимумы функции: -1
13. Точки максимума: 2*pi*n
14. Максимумы функции: 2*pi*n
Функция tg(x)
1. Область определения: (-pi/2 +pi*n; pi/2 +pi*n)
2. Область значений: R
3. Нечетная
4. Наименьший положительный период: pi
5. Координаты точек пересечения графика функции с осью Ох: (pi*n; 0)
6. Координаты точек пересечения графика функции с осью Оу: (0;0)
7. Промежутки, на которых функция положительна: (pi*n; pi/2 +pi*n)
8. Промежутки, на которых функция отрицательна: (-pi/2 +pi*n; pi*n)
9. Промежутки возрастания: (-pi/2 + pi*n; pi/2 + pi*n)
10. Промежутки убывания: нет
11. Точки минимума: нет
12. Минимумы функции: нет
13. Точки максимума: нет
14. Максимумы функции: нет
Функция ctg(x)
1. Область определения: (pi*n; pi +pi*n)
2. Область значений: R
3. Нечетная
4. Наименьший положительный период: pi
5. Координаты точек пересечения графика функции с осью Ох: (pi/2 + pi*n; 0)
6. Координаты точек пересечения графика функции с осью Оу: нет
7. Промежутки, на которых функция положительна: (pi*n; pi/2 +pi*n)
8. Промежутки, на которых функция отрицательна: (-pi/2 +pi*n; pi*n)
9. Промежутки возрастания: нет
10. Промежутки убывания: (pi*n; pi +pi*n)
11. Точки минимума: нет
12. Минимумы функции: нет
13. Точки максимума: нет
14. Максимумы функции: нет
Гармонические колебания
Колебания, которые происходят согласно следующим законам
f(t) = A*cos(w*t+f),
f(t) = A*sin(w*t+f),
называются гармоническими.
Здесь A – амплитуда колебания, w – циклическая частота, f – начальная фаза колебания. Время, за которое совершается одно полное колебание, называется периодом. Период гармонических колебаний равен 2*pi/w.
Графиками гармонических колебаний будут косинусоида и синусоида. Примером гармонических колебаний, являются колебания шарика подвешенного на пружине.
Нужна помощь в учебе?
Предыдущая тема: Периодичность тригонометрических функций: четные и нечетные
Следующая тема:   Решение простейших тригонометрических уравнений: графики и примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
