Тангенс выразить через синус: Размещение рекламы на Studygide.ru

alexxlab / / Разное

Тригонометрия: основные формулы — intmag24.ru

Опубликовано от Admin — Оставить комментарий

Тригонометрия (определения и основные формулы) являются одной из базовых тем геометрии. Соотношения между основными тригонометрическими функциями (синусом, косинусом, тангенсом и котангенсом) задаются тригонометрическими формулами. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье по порядку перечислены все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Определение

Прямые тригонометрические функции

sin

Синус угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.

cos

Косинус угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.

Производные тригонометрические функции
tg

Тангенс угла в прямоугольном треугольнике– это отношение противолежащего катета к прилежащему.

ctg

Котангенс угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.

Другие тригонометрические функции

 

sec

Секанс угла в прямоугольном треугольнике — отношение гипотенузы к прилежащему катету

cosec

Косеканс угла в прямоугольном треугольнике — отношение гипотенузы к противолежащему катету.

Тригонометрия: основные тригонометрические формулы
Основные тригонометрические тождества

задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они позволяют выразить одну тригонометрическую функцию через другую.

Формулы суммы и разности тригонометрических функций 

предназначены для упрощения тригонометрических выражений. Они используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители, сумму и разность синусов и косинусов.

Формулы произведения тригонометрических функций 

предназначены для упрощения тригонометрических выражений. Они используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители, сумму и разность синусов и косинусов.

Формулы произведения тригонометрических функций  в степени

Формулы сложения и вычитания аргументов

Формулы двойного, половинного и тройного углов
Формулы понижения степени

Тригонометрия: основные значения

Угол, градусы

0°

30°

45°

60°

90°

120°

180°

270°

360°

sin

0

1/2

√2/2

√3/2

1

√3/2

0

-1

0

cos

1

√3/2

√2/2

1/2

0

-1/2

-1

0

1

tg

0

√3/3

1

√3

—

-√3

0

—

0

ctg

—

√3

1

√3/3

0

-√3/3

—

0

—

sec

1

2√3/3

√2

2

—

-2

-1

—

1

cosec

—

2

√2

2√3/3

1

2√3/3

—

-1

—

Угол, радианы

0

π/6

π/4

π/3

π/2

2π/3

π

3π/2

2π

 

 

Рубрика: Для школьников

Метки Математика, Геометрия

Основные формулы тригонометрии — Без Сменки

26 мая, 2022

1 мин

Самая полезная формула в тригонометрии — основное тригонометрическое тождество. Из него можно выразить синус через косинус, или наоборот косинус через синус. 

✅А если вспомнить, что тангенс — это отношение синуса к косинусу, а котангенс — это тангенс наоборот, то можно найти еще две формулы: тангенс, если известен только косинус, и котангенс, если известен только синус. Все самые полезные формулы в одной картинке для тебя. Наслаждайся! 

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Честно. Понятно. С душой.

40 подписчиков

+ Подписаться

Редакция Без Сменки

07 июня, 2022

1 мин

Англ 🇬🇧

Пунктуация в английском языке

♦️ Когда ставим запятую в английском? 1️⃣ Перед вводными словами и выражениями (кстати, не. ..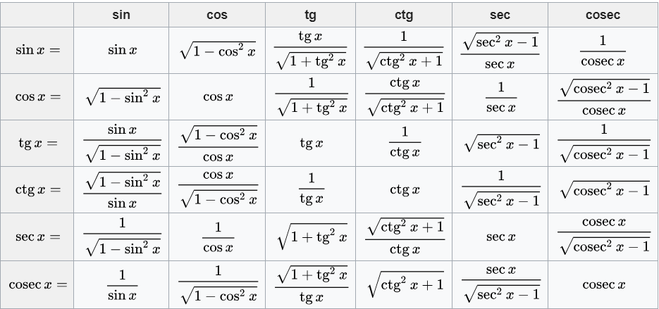

Редакция Без Сменки

11 января, 2022

1 мин

Био 🦠

Термины генетики

Генетика — это не только 28 задание в ЕГЭ по биологии! Вопросы по ней могут встретиться и в тесте,…

Редакция Без Сменки

01 июля, 2022

1 мин

Лит 📚

Анафора и эпифора

Из пункта А в пункт Э выехали художественные средства, основанные на повторе. Это были Анафора…

Редакция Без Сменки

29 июня, 2022

1 мин

Ист 🤴

Крымская война [1853-1856 гг. ]

Разбираем одну из самых важных войн в XIX веке, которую иногда даже называют «нулевой мировой». …

Редакция Без Сменки

06 июня, 2022

1 мин

Общ 👨‍👩‍👧

Государство и его функции

Теперь о признаках: 🔹 наличие публичной власти — это те или иные органы законодательной и…

Редакция Без Сменки

03 июня, 2022

1 мин

Ист 🤴

Дворцовые перевороты

👉🏻 ПРИЧИНЫ ДВОРЦОВЫХ ПЕРЕВОРОТОВ: — 1722 г.

2}$$ Фух. 92-1}\,dx$

Tan Theta Formula — GeeksforGeeks

Тангенс — это функция в тригонометрии, которая представляет собой раздел математики, занимающийся специфическими функциями углов. Он имеет дело с соотношением между длинами сторон и углами треугольников. Он в основном используется для нахождения неизвестных длин сторон, углов прямоугольного треугольника с использованием тригонометрических функций и формул. Есть шесть функций, которые широко используются в тригонометрии. Это синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (cosec). В этой статье мы собираемся обсудить формулу тангенса θ.

Что такое тан тета?

tan θ — это часто используемая тригонометрическая функция наряду с другими 5 функциями. tan θ также называется законом тангенса. Формулу тангенса прямоугольного треугольника можно определить как отношение противоположной стороны треугольника к прилежащей стороне. Его также можно представить как отношение синуса угла к косинусу угла.

Прямоугольный треугольник

tan θ = Противоположная сторона/Смежная сторона

где.

θ — один из острых углов.

Ниже приведены значения загара под разными углами.

θ

0°

30°

45°

60°

90°

tan θ

0

1/√3

1

√3

∞

Важные формулы для

TAN THETA
  • TAN (θ) = SIN (θ)/COS (θ)
  • TAN (θ) = SIN (θ)/COS (θ)
  • . cot(θ)
  • tan 2 (x)=sec 2 (x)-1
  • tan(-x)=-tan(x)
  • tan(90 o -x)=cot( x)
  • tan(x+π)=tan(x)
  • tan(π-x)=-tan(x)
  • tan(x+y)= \frac{tan(x)+tan(y) }{1-tan(x). tan(y)}
  • tan(xy)= \frac{tan(x)-tan(y)}{1+tan(x).tan(y)} 92(x)}
  • tan(x/2)=\sqrt{\frac{1-cos(x)}{1+cos(x)}}

Примеры вопросов

Вопрос 1. Найдите θ для прямоугольного треугольника, если длина противоположной стороны и смежной стороны относительно θ равны 3 см и 3√3 см соответственно.

Решение:

Дано

Длина противоположной стороны = 3 см

Длина смежной стороны = 3√3 см0005

= 3/3√3

= 1/√3

TAN 30 ° = 1/√3

TAN (θ) = TAN 30 °

θ = 30 °

Вопрос 2: Найдите TAN θ для данной COT θ = 0.

Решение:

Указано

Cot θ = 0

Связь между Tanθ и COTθ, то есть,

TAN θ = 1/COT θ

=1/0

тангенс θ = ∞

Вопрос 3: Найдите тангенс θ по заданным sin θ = 1/2 и cos θ = √3/2.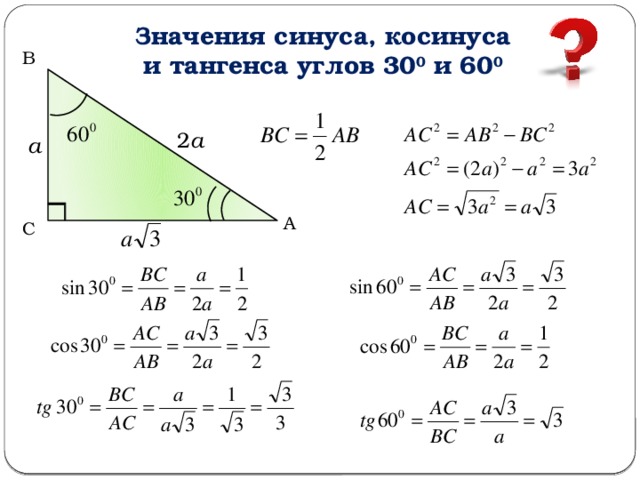

Решение:

Дано,

sin θ = 1/2

cos θ = √3/2

tan θ = 0 √ 0 9 / cos 0 9 3/2)

= (1×2) / (2×√3)

тангенс θ = 1/√3

Вопрос 4: Найдите тангенс х по заданной секунде х=2/5.

Решение:

Учитывая

сек x = 2/5

мы знаем, что сек 2 x – тангенс 2 x = 1

Из этого тангенса 2 х = сек 2 х – 1

= (2/5) 2 -1

= (4/25)-1

= (4-25)/25

tan 2 (x) = -21/25

tan(x) = √(-21/25)

tan(x) = √(-21)/5

32 Вопрос : Найдите результат загара (60°+45°).

Решение:

Дано

A=60° 

B=45°

Мы знаем, что tan(A+B)= \frac{tan(A)+tan(B)}{1 -загар(А).загар(В)}

tan(60°+45°)=\frac{tan(60°)+tan(45°)}{1-tan(60°).

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *