Функция модуль числа – Модуль числа — Youclever.org

Модуль числа в Python 3 — Функция abs библиотеки math

Очень часто возникает необходимость вычисления модуля числа в Python. Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.

Модуль числа

Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.

При вычислении модуля возможны 3 ситуации:

• Когда число больше 0. Если взять его по модулю — не изменится.
• Модуль нуля так же равен нулю.
• У отрицательного числа отбрасываем знак. То есть умножаем его на -1.

Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?

Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.

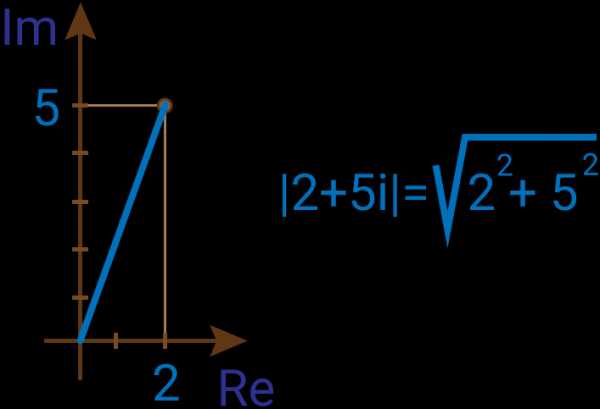
Исходя из теоремы Пифагора получаем, что модуль комплексного числа это корень квадратный из суммы квадратов мнимой и действительной частей.

Вычисление

Вычислять модуль можно следующими способами:

• Используя стандартную функцию abs.
• С помощью функции fabs библиотеки math.
• При помощи самостоятельно написанной функции.

Все эти функции работают как в Python 2, так и в Python 3.

abs

Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.

a = -10
b = abs(a)
print(b)
print(type(b))

10
<class 'int'>

fabs

Можно так же воспользоваться функцией fabs из библиотеки math. Библиотеку можно подключить с помощью from math import fabs.

from math import fabs
a = -10
b = fabs(a)
print(b)
print(type(b))

10.0
<class 'float'>

Отличие abs от fabs заключается в том, что функция abs возвращает значение того же типа, что и аргумент. Функция же fabs вначале преобразует тип аргумента к вещественному числу.

Свое решение

Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.

Например, можно вычислить воспользоваться тернарным оператором.

a = -10
b = a if a > 0 else -a
print(b)

10

На основе такого условия сделаем свою функцию.

def my_abs(a):
    return a if a > 0 else -a
print(my_abs(-3))

3

Модуль комплексного числа

Мы разобрались как происходит вычисление с действительными числами. Теперь посмотрим, как в языке программирования Python можно получить модуль комплексного.

Функцией fabs мы не сможем воспользоваться. Если попытаемся это сделать, то получим ошибку приведения комплексного числа к действительному (TypeError).

from math import fabs
a = -10-2j
b = fabs(a)
print(b)

Traceback (most recent call last):
  File "main.py", line 3, in <module>
    b = fabs(a)
TypeError: can't convert complex to float

А вот с помощью abs преобразование удается.

a = -10-2j
b = abs(a)
print(b)

10.19803902718557

Или же напишем свою функцию:

from math import sqrt
def my_abs_complex(c):
    return sqrt(c.real**2 + c.imag**2)
a = -10-2j
b = my_abs_complex(a)
print(b)

10.198039027185569

Результаты получились одинаковыми. Но нам все равно пришлось подключить библиотеку math для вычисления квадратного корня.

all-python.ru

Модуль числа в Excel | TutorExcel.Ru

Выясним как посчитать модуль числа в Excel с помощью функции ABS, а также дополнительно рассмотрим несколько различных вариантов вычисления формулы модуля.

Для нахождения значения по модулю в Excel существует стандартная функция ABS.
В общем и целом поиск абсолютного значения является достаточно простой операцией для вычисления, поэтому данная функция является стандартной во многих языках программирования, к примеру, на языке VBA (Visual Basic for Applications) формула модуля также записывается как Abs.

Функция модуля в Excel

Синтаксис и описание функции ABS:

ABS(число)
Возвращает модуль (абсолютную величину) числа.

• Число (обязательный аргумент) — действительное число, модуль которого требуется посчитать.

В качестве аргумента функции задаем произвольное действительное число, в результате получаем его абсолютную величину:

Несмотря на то, что знак модуля в математике обозначается как вертикальная черта |, попытка поставить знак модуля в Excel для поиска значения по модулю приведет к ошибке, например, при вводе формулы =|-29| Excel выдаст ошибку.

Альтернативные способы расчета

Если вдруг формула ABS вылетела из головы, и Вы забыли как посчитать модуль в Excel с ее помощью, то рассмотрим несколько способов поиска абсолютной величины числа без использования данной формулы.

С помощью функции ЗНАК

Согласно определению, модуль — это неотрицательное значение исходного числа, поэтому умножая число на 1 или -1 в зависимости от знака числа (то есть положительное умножаем на 1, отрицательное умножаем на -1), мы в итоге получим абсолютную величину:

С помощью функции КОРЕНЬ

Чтобы найти модуль мы также можем воспользоваться свойством вычисления квадратного корня в Excel.
Напомним, что в Excel используется понятие арифметического корня для вычисления корней четных степеней.
Другими словами, корень четной степени в Excel всегда принимает неотрицательное значение, поэтому при извлечении квадратного корня от числа возведенного в квадрат, мы опять в результате получим абсолютную величину:

Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!

Поделиться с друзьями:

Поиск по сайту:

tutorexcel.ru

Функция модуль в Excel

Модуль – это абсолютная положительная величина любого числа. Даже у отрицательного числа модуль будет всегда положительным. Давайте выясним, как рассчитать величину модуля в приложении Microsoft Excel.

Функция ABS

Для расчета величины модуля в приложении Excel существует специальная функция под названием ABS. Синтаксис этой функции очень простой: «ABS(число)». Либо, формула может принимать такой вид «ABS(адрес_ячейки_с_числом)».

Для того, чтобы рассчитать, например, модуль от числа -8, нужно вбить в строку формул или в любую ячейку на листе, следующую формулу: «=ABS(-8)».

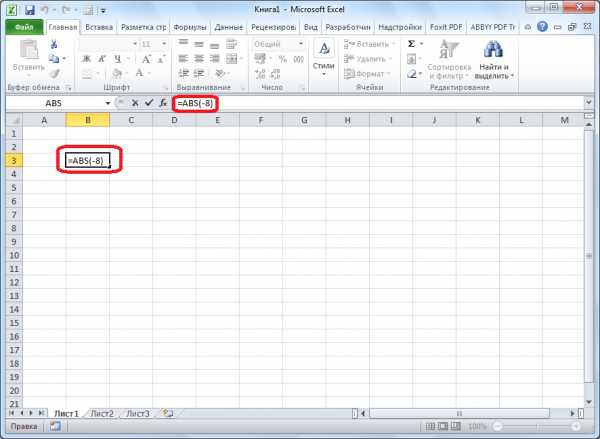
Чтобы произвести расчет, жмем на кнопку ENTER. Как видим, программа выдает в ответ положительное значение числа 8.

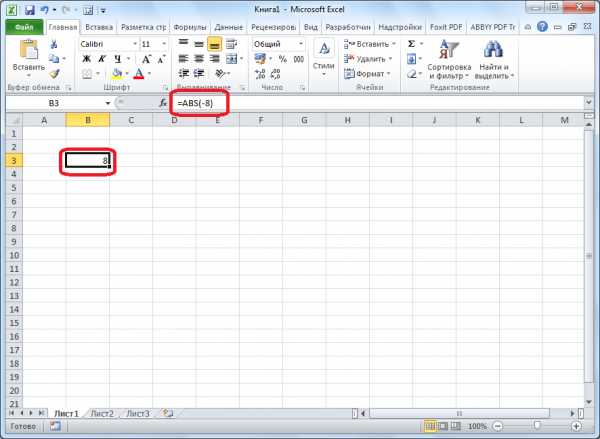
Существует ещё один способ расчета модуля. Он подойдет для тех пользователей, которые не привыкли держать в голове различные формулы. Кликаем по ячейке, в которой хотим, чтобы хранился результат. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.

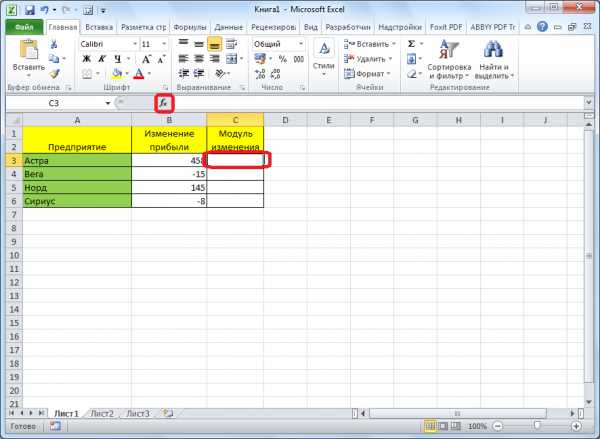
Запускается окно Мастера функций. В списке, который расположен в нем, нужно найти функцию ABS, и выделить её. Затем нажимаем на кнопку «OK».

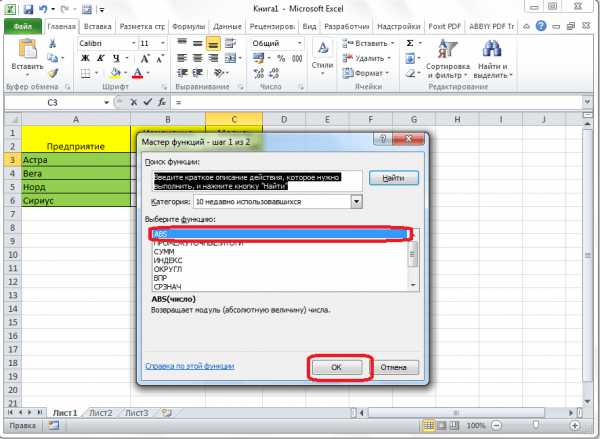
Открывается окно аргументов функции. Функция ABS имеет всего один аргумент — число. Вводим его. Если же вы хотите взять число из данных, которые хранятся в какой-либо ячейке документа, то нажмите на кнопку, размещенную справа от формы ввода.

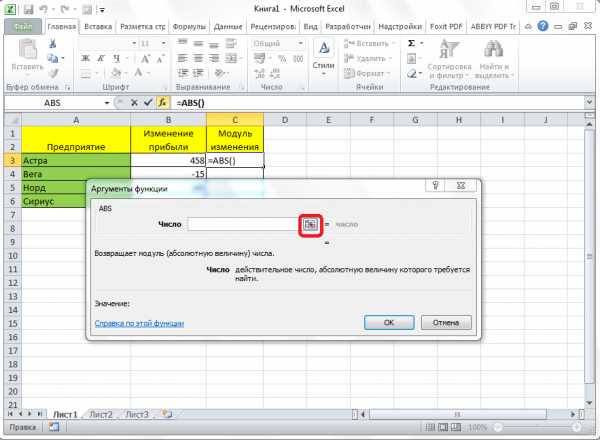
После этого, окно сворачивается, а вам нужно кликнуть по ячейке, где содержится число, от которого хотите рассчитать модуль. После того, как число добавлено, опять жмите на кнопку справа от поля ввода.

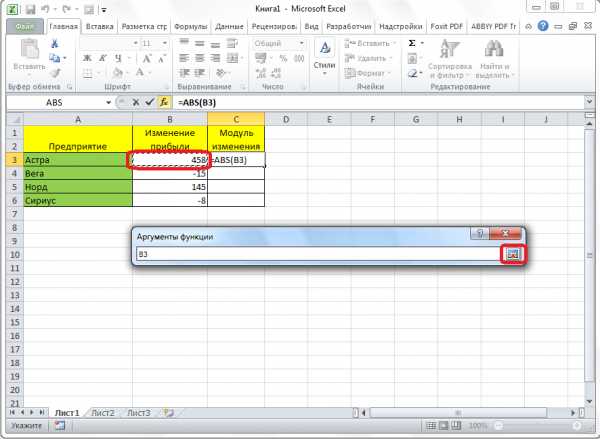
Снова запускается окно с аргументами функции. Как видим, поле «Число» заполнено значением. Жмем на кнопку «OK».

Вслед за этим, в ранее указанной вами ячейке выводится значение модуля того числа, которое вы выбрали.

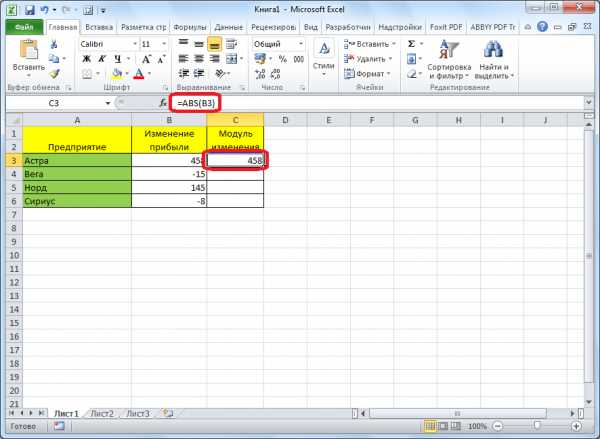
Если значение расположено в таблице, то формулу модуля можно скопировать и на другие ячейки. Для этого, нужно стать на нижний левый угол ячейки, в которой уже есть формула, зажать кнопку мыши, и провести ею вниз до конца таблицы. Таким образом, в данном столбце в ячейках появятся значение по модулю исходных данных.

Важно заметить, что некоторые пользователи пытаются записать модуль, как это принято в математике, то есть |(число)|, например |-48|. Но, в ответ они получают ошибку, так как Excel не понимает подобный синтаксис.

Как видим, в расчете модуля из числа в приложении Microsoft Excel нет ничего сложного, так как данное действие выполняется с помощью простой функции. Единственное условие состоит в том, что данную функцию нужно просто знать.

Помогла ли вам эта статья?

lumpics.ru

Модуль числа Вики

Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.

В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

 |x|={  x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}

Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной^[1]. Он определяется по формуле:

|z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}

Основные свойства[ | код]

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина |x1−x2|{\displaystyle |x_{1}-x_{2}|} означает расстояние между точками x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Вещественные числа[ | код]

• Область определения: (−∞;+∞){\displaystyle (-\infty ;+\infty )}.
• Область значений: [0;+∞){\displaystyle [0;+\infty )}.
• Функция чётная.
• Функция дифференцируема всюду, кроме нуля. В точке x=0{\displaystyle x=0} функция претерпевает излом.

Комплексные числа[ | код]

Алгебраические свойства[ | код]

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие соотношения:

•  |x|=x2=x⋅sgn⁡x=max{x,−x}{\displaystyle \ |x|={\sqrt {x^{2}}}=x\cdot \operatorname {sgn} x={\rm {max}}\,\{x,\,-x\}} (см. Функция sgn(x)).
• a⩽|a|{\displaystyle a\leqslant |a|}
• −|a|⩽a{\displaystyle -|a|\leqslant a}.
• Квадрат модуля числа равен квадрату этого числа: |a|2=a2{\displaystyle |a|^{2}=a^{2}}

Как для вещественных, так и для комплексных a,b{\displaystyle a,b} имеют место соотношения:

История[ | код]

Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

В языках программирования[ | код]

Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа. В программе Wolfram Mathematica Abs[x].

Обобщение[ | код]

Понятие абсолютной величины можно ввести в произвольном упорядоченном кольце или упорядоченном поле, и свойства её будут аналогичны приведенным выше.

Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую ‖x‖{\displaystyle \|x\|}. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.

См. также[ | код]

Примечания[ | код]

ru.wikibedia.ru

Модуль действительного числа, функция модуля

Работа устно

Работа устно

Работа устно

• Решить уравнения:

Построение графика функции

у= |x+m|+t

Домашнее задание

№ 16.15

№ 16.16 (г)

№ 16.19

№ 16.36 (а)

Повторение теории

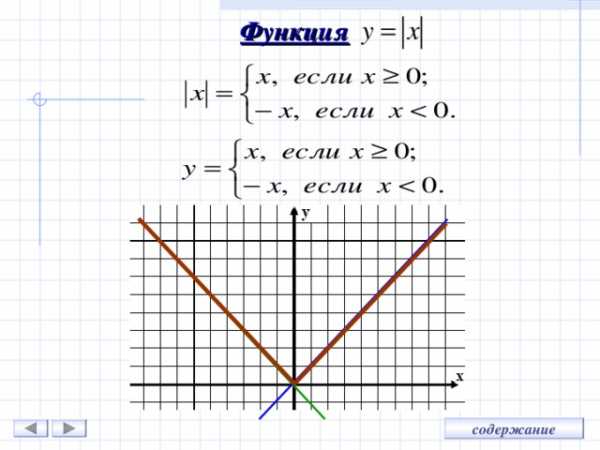
Определение : модулем неотрицательного действительного числа х называют само это число; модулем отрицательного действительного числа х называют противоположное число.

| x | — расстояние от 0 до х

Геометрический смысл модуля

x

5

-5

0

|5| = 5 , т.к. расстояние от 0 до 5 равно 5

| — 5| = 5 , т.к. расстояние от 0 до -5 равно 5

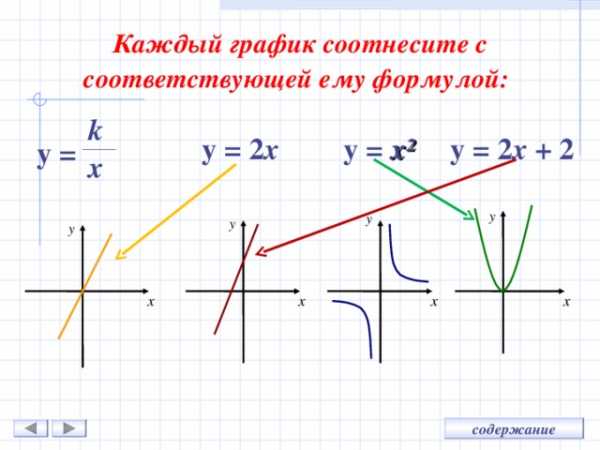
Каждый график соотнесите с соответствующей ему формулой:

k

y = 2 x + 2

y = 2 x

y = x²

y =

x

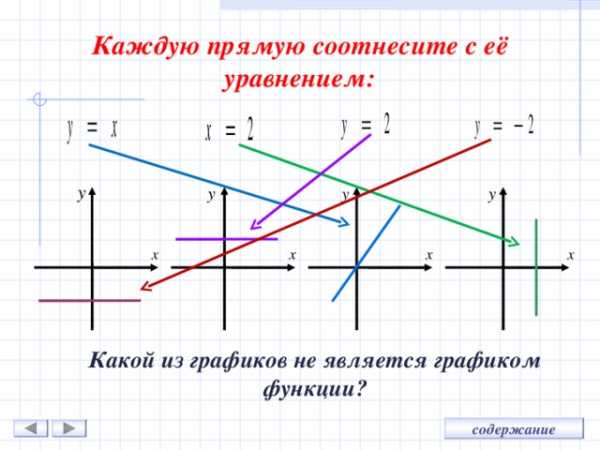
Каждую прямую соотнесите с её уравнением:

Какой из графиков не является графиком функции?

Повторение

формула

график

название

Прямая, 2 точки

Линейная

Парабола, 5 точек, в середине вершина

Квадратичная

Ветка параболы относительно оси Ох, 4 точки

Квадратный корень

Кубическая парабола

Степенная

y = | х |

Модуль

«Галочка»

Функция

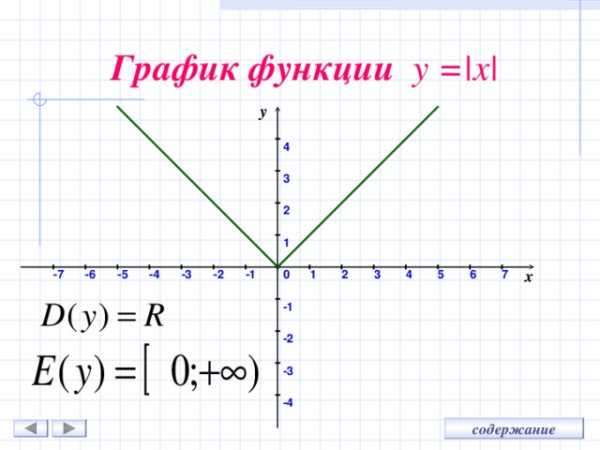
График функции у = |x|

y

4

3

2

1

x

5

6

4

7

3

2

-5

1

-1

-2

-3

-4

-6

-7

0

-1

-2

-3

-4

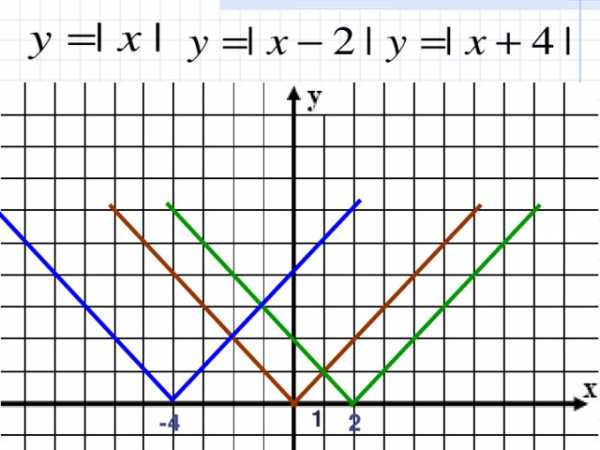
С помощью графика функции y = |x|

можно построить график функции

y = |x + m| методом движения вдоль оси Ох на m единиц:

влево , если m 0

вправо , если m

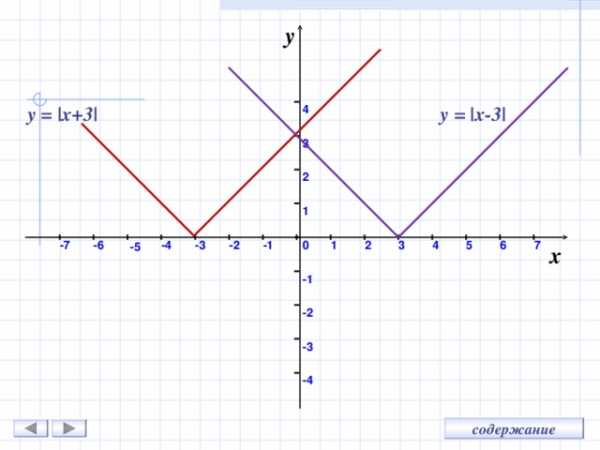
y

y = |x+ 3 |

y = |x-3|

4

3

2

1

-2

-3

7

0

6

5

4

-4

3

2

1

-7

-6

-1

-5

x

-1

-2

-3

-4

1

2

-4

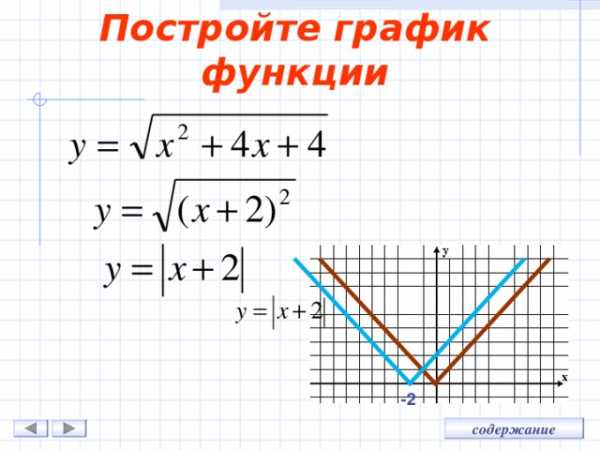
Постройте график функции

-2

С помощью графика функции y = |x| можно построить график функции

y = |x|+t методом движения вдоль оси Оу на t единиц:

вверх , если t 0

вниз , если t

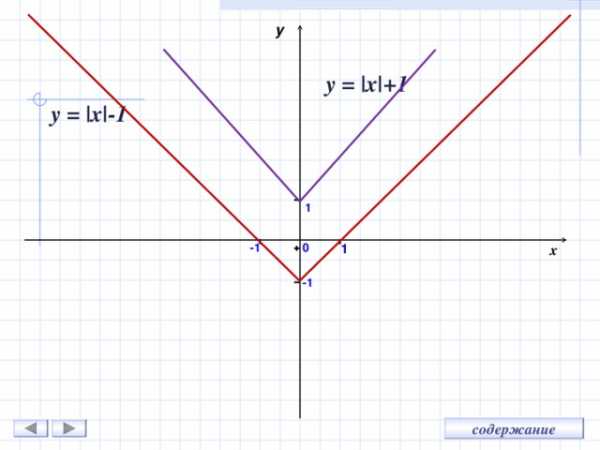
y

y = |x| + 1

y = |x| -1

1

-1

x

0

1

-1

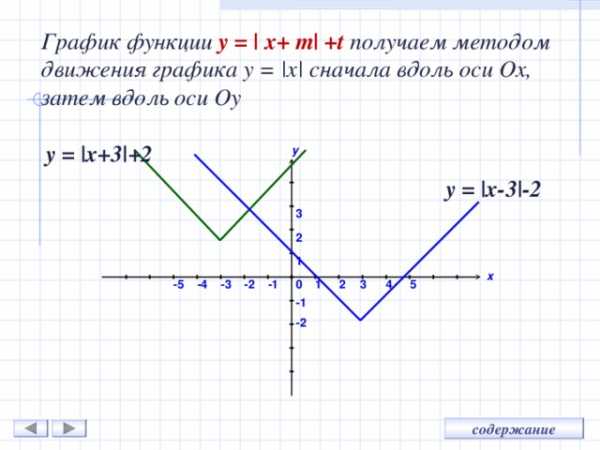
График функции y = | x+ m| +t получаем методом движения графика y = |x| сначала вдоль оси O х, затем вдоль оси O у

y = |x+3|+2

y

y = |x-3|-2

3

2

1

x

4

1

-2

2

-3

3

-1

-4

5

-5

0

-1

-2

у

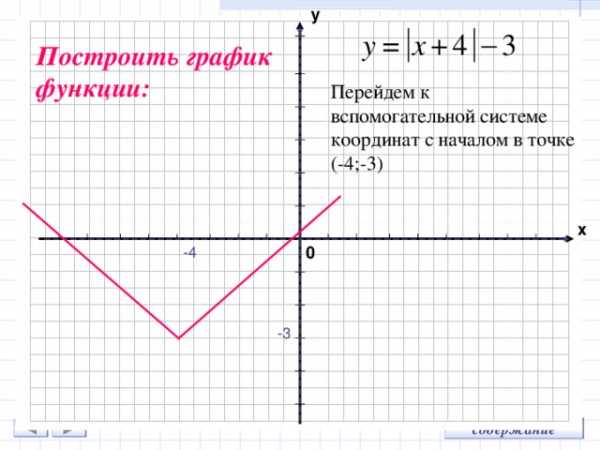
Построить график функции:

Перейдем к вспомогательной системе координат с началом в точке (-4;-3)

х

0

— 4

— 3

Самостоятельная работа

В самостоятельной работе 6 заданий . Вам необходимо определить каким уравнением задаётся график функции.

Найти его среди предложенных ответов.

Записать себе в тетрадь номер задания и вариант ответа.

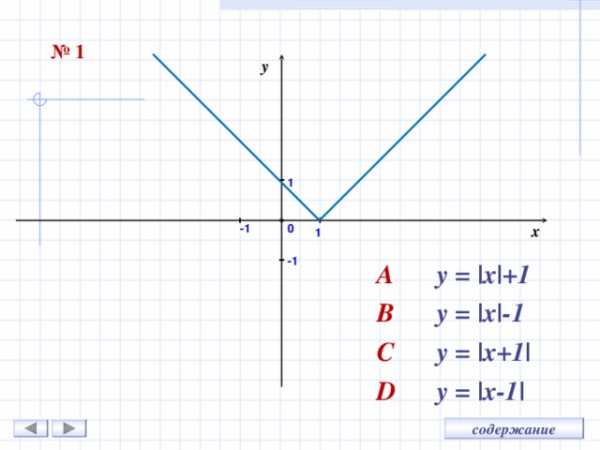
№ 1

y

1

x

0

-1

1

A y = |x|+1

B y = |x|-1

C y = |x+1|

D y = |x-1|

-1

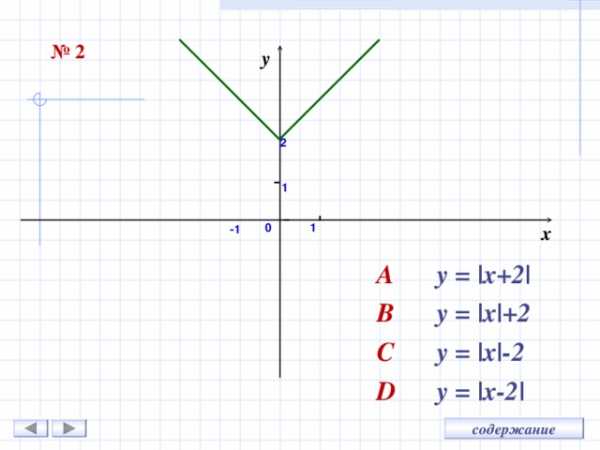
№ 2

y

2

1

0

x

1

-1

A y = |x+2|

B y = |x|+2

C y = |x|-2

D y = |x-2|

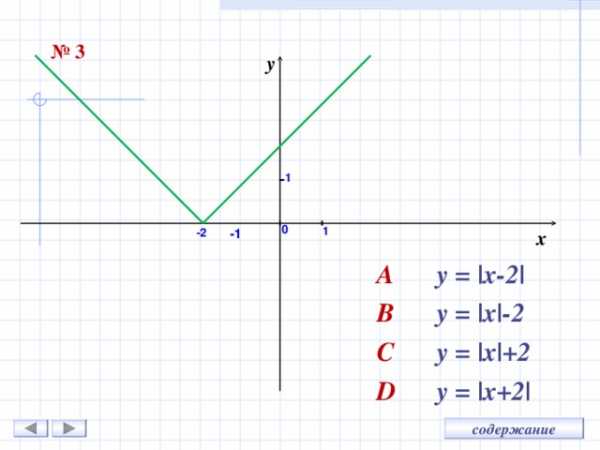
№ 3

y

1

0

1

x

-1

-2

A y = |x- 2 |

B y = |x|- 2

C y = |x|+ 2

D y = |x+ 2 |

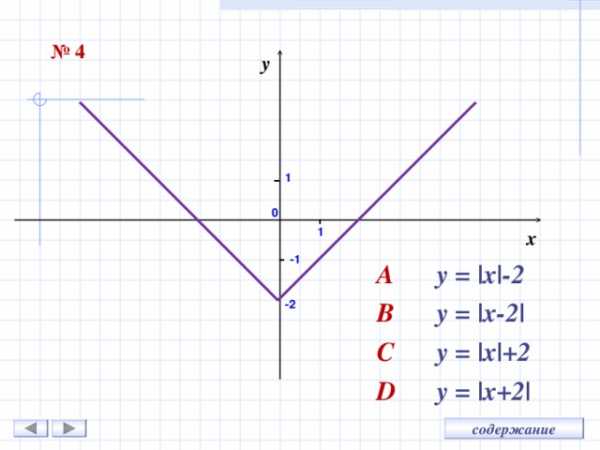
№ 4

y

1

0

1

x

-1

A y = |x|- 2

B y = |x- 2 |

C y = |x|+ 2

D y = |x+ 2 |

-2

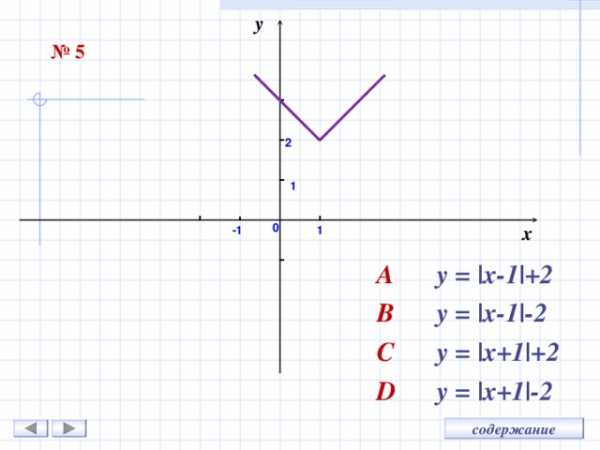
y

№ 5

2

1

0

x

-1

1

A y = |x -1 |+ 2

B y = |x -1 | — 2

C y = |x +1 |+ 2

D y = |x+ 1 |-2

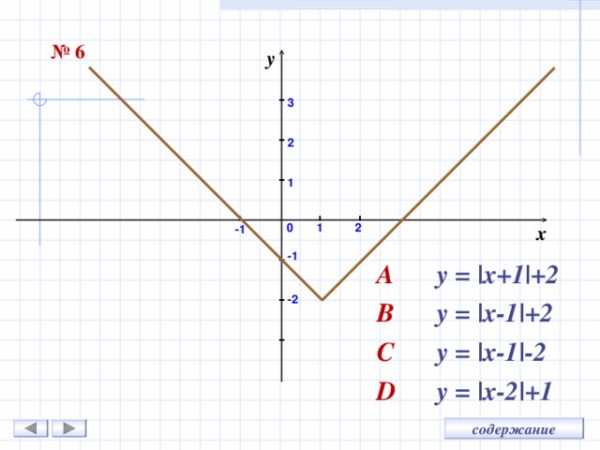
№ 6

y

3

2

1

0

1

2

x

-1

-1

A y = |x+1|+2

B y = |x-1|+2

C y = |x-1|-2

D y = |x-2|+1

-2

Проверьте свои ответы по ключу

• Задание 1 – D
• Задание 2 – B
• Задание 3 – D
• Задание 4 – A
• Задание 5 – A
• Задание 6 – С

Оценка самостоятельной работы

• Нет ошибок — 5 (пять) .
• Одна ошибка — 4 (четыре).
• Две ошибки — 3 (удовлетворительно)

videouroki.net

Модуль числа Википедия

Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.

В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

 |x|={  x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}

Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной^[1]. Он определяется по формуле:

|z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}

Основные свойства

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина |x1−x2|{\displaystyle |x_{1}-x_{2}|} означает расстояние между точками x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Вещественные числа

• Область определения: (−∞;+∞){\displaystyle (-\infty ;+\infty )}.
• Область значений: [0;+∞){\displaystyle [0;+\infty )}.
• Функция чётная.
• Функция дифференцируема всюду, кроме нуля. В точке x=0{\displaystyle x=0} функция претерпевает излом.

Комплексные числа

Алгебраические свойства

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие соотношения:

•  |x|=x2=x⋅sgn⁡x=max{x,−x}{\displaystyle \ |x|={\sqrt {x^{2}}}=x\cdot \operatorname {sgn} x={\rm {max}}\,\{x,\,-x\}} (см. Функция sgn(x)).
• a⩽|a|{\displaystyle a\leqslant |a|}
• −|a|⩽a{\displaystyle -|a|\leqslant a}.
• Квадрат модуля числа равен квадрату этого числа: |a|2=a2{\displaystyle |a|^{2}=a^{2}}

Как для вещественных, так и для комплексных a,b{\displaystyle a,b} имеют место соотношения:

История

Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

В языках программирования

Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа. В программе Wolfram Mathematica Abs[x].

Обобщение

Понятие абсолютной величины можно ввести в произвольном упорядоченном кольце или упорядоченном поле, и свойства её будут аналогичны приведенным выше.

Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую ‖x‖{\displaystyle \|x\|}. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.

См. также

Примечания

wikiredia.ru

Модуль в Excel. Модуль в Эксель. Функция ABS. Формула модуля в таблицах

Продолжаем серию статей о математических формулах в Excel. Сегодня разберем формулу записи «модуль в Excel». Модуль числа применяется для определения абсолютной величины числа, например длины отрезка. Ниже мы приводим несколько способов расчета модуля числа в Эксель, основная функция — ABS, а дополнительный расчет при помощи функций ЕСЛИ и КОРЕНЬ.

Как следует из определения, модуль числа — это неотрицательное число, значение самого числа. Т.е. если у нас есть отрицательное число -7, то по модулю оно будет равняться 7. Записывается модуль как две вертикальные линии:

|-7| = 7

Для чего применяется? Если у нас есть значение вектора равное -7, где минус обозначает его обратное направление, то чтобы найти длину самого вектора, нам необходимо высчитать модуль числа (т.к. длина не может быть отрицательной величиной).

Так же довольно часто, использование модуля можно встретить при расчете отрицательного значения времени, но про это у нас есть отдельная статья.

=ABS()

=ЕСЛИ(A1<0;A1*-1;A1)

=КОРЕНЬ(A1*A1)

A=Abs(-7)