Высшая математикаВекторыОпределение
Сложение векторовСумма нескольких векторовВычитание векторовУмножение вектора на числоПример
Проекция вектора на осьКоординатные векторыРазложение вектора на составляющиеФормула модуля вектораКоординаты вектораСкалярное произведение векторовОпределение
Физический смысл скалярного произведения
Выражение скалярного произведения через координаты перемножаемых векторов
Свойства скалярного произведенияПримерПример
Векторное произведениеОпределение
Обозначение векторного произведения векторовПонятие «правой» тройки векторов
Векторные произведения координатных векторовВыражение векторного произведения через координаты перемножаемых векторовПример
Свойства векторного произведенияПримерНаправляющие косинусы вектораФормула связи направляющих косинусовЕдиничный вектор
Координаты единичного вектораПример
Физический смысл векторного произведенияУсловия коллинеарности двух векторовКомпланарные векторы
Условия компланарности трёх векторовКоллинеарные векторы
Условие коллинеарности двух векторовНекоторые кривыеПоверхности второго порядка |
rpp.nashaucheba.ru
Лекция Векторная алгебра. Векторы.
Скачать с Depositfiles
ВЕКТОРНАЯ АЛГЕБРА
Лекция № 4. Тема 1 : Векторы
1.1. Определение вектора
Все величины, с которыми нам приходилось встречаться до настоящего времени в физике, технике были двух видов: скалярные, которые харак-теризуются одним числовым значением и векторные, характеризуются числовым значением и направлением.
Пример 1. Скалярные величины: масса, объём, температура и т.д. Векторные величины: сила, скорость, ускорение и т. д.
Определение 1. Направленный отрезок называется вектором и обозна-чается 
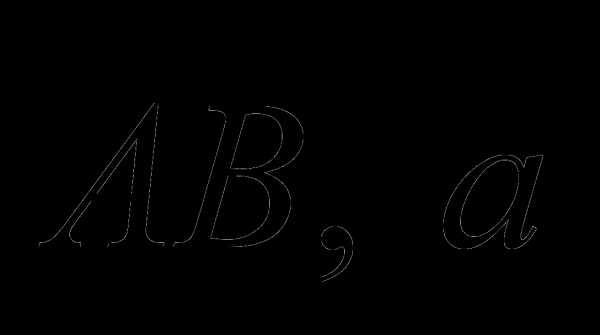 .А
.А
Определение 2. Расстояние между началом и концом вектора называется его длиной или модулем и обозначается
Если  или
или 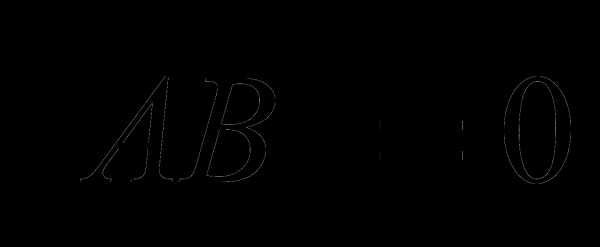 , то векторы называются соответственно единичным и нулевым.
, то векторы называются соответственно единичным и нулевым.
Определение 3. Векторы называются коллинеарными, если существует прямая, которой они параллельны.
Определение 4. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Определение 5. Два вектора называются равными, если они коллине-арные, одинаково направлены и имеют равные модули (равные длины).
Пусть задан некоторый вектор  и ось l.
и ось l.
Определение 6. Проекцией вектора 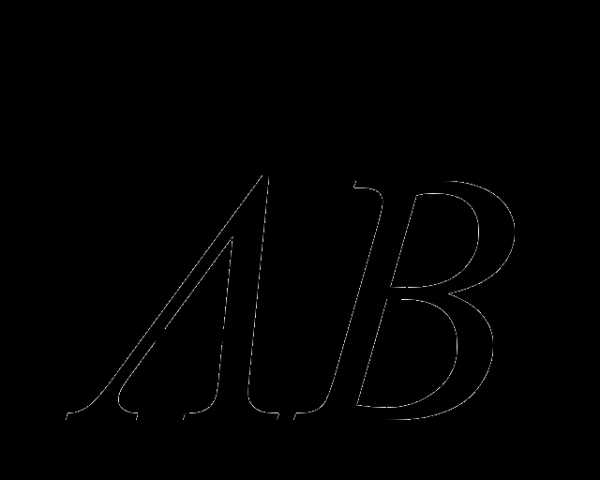 на ось l называется величина где
на ось l называется величина где  угол между вектором
угол между вектором 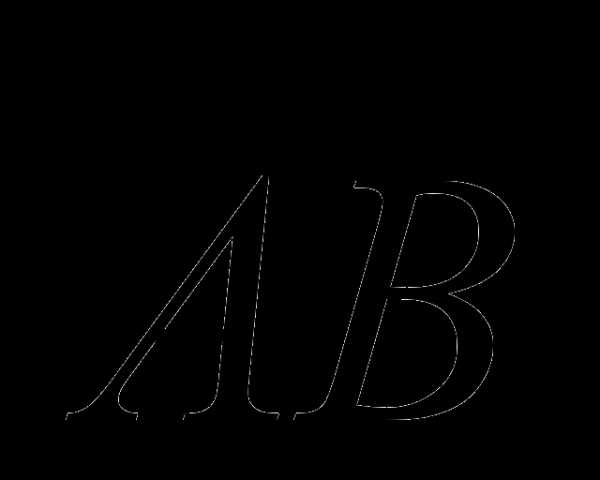 и осью l.
и осью l.
В
А

l
1.2. Линейные операции над векторами
1. Произведение вектора на число.
Определение 7. Произведением вектора  на число
на число 
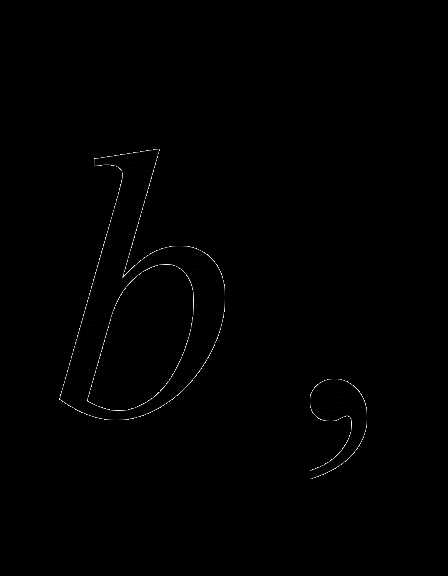 определяемый следующими условиями: вектор
определяемый следующими условиями: вектор 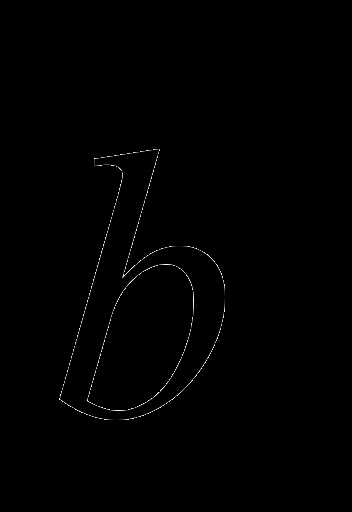 коллинеарен вектору
коллинеарен вектору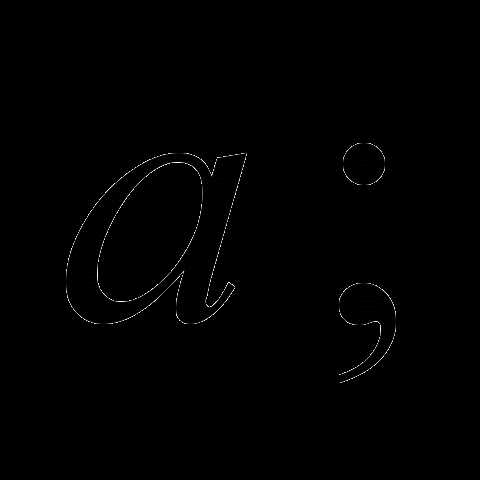 векторы
векторы 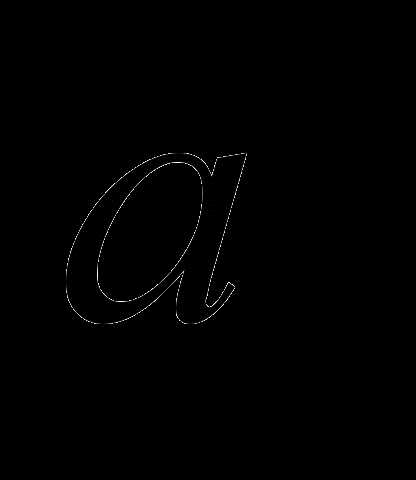 и
и 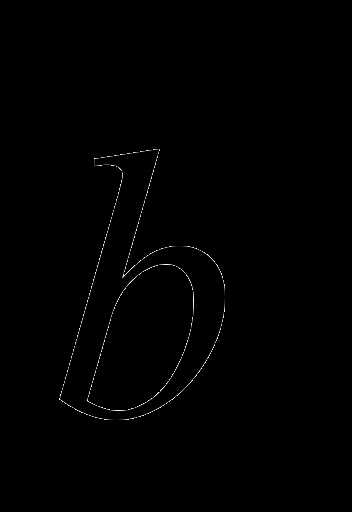 одинаково направлены, если
одинаково направлены, если 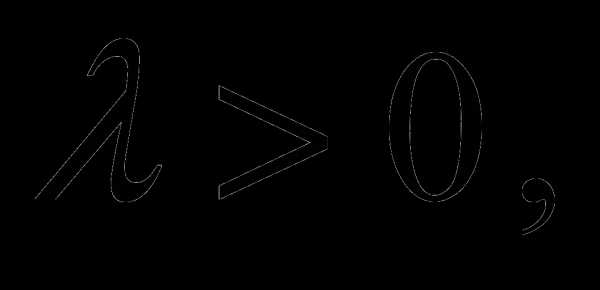 и противоположны, если
и противоположны, если 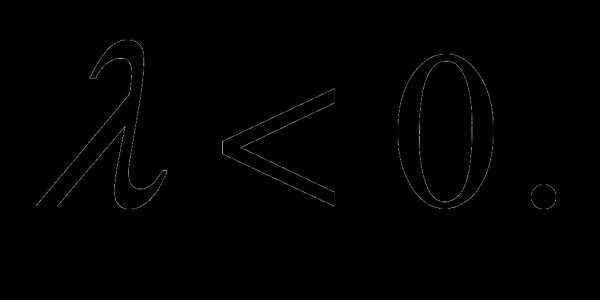
Пример 2. Построить вектор 
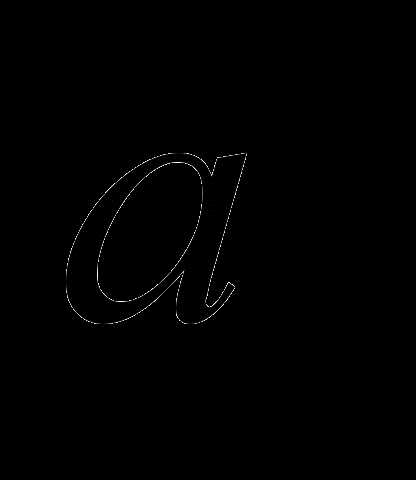


Из этого определения следует условие коллинеарности двух векторов:
Пусть  ненулевой вектор, тогда для любого коллинеарного ему вектора
ненулевой вектор, тогда для любого коллинеарного ему вектора 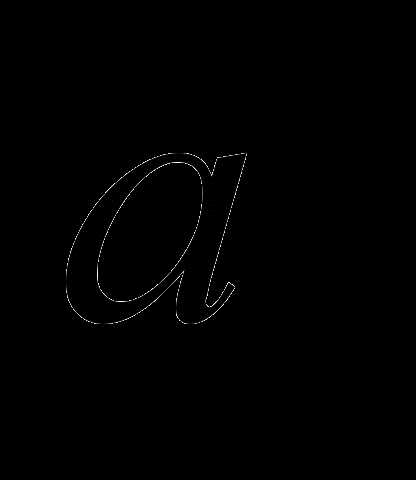 существует единственное число
существует единственное число  удовлетворяющее равенству
удовлетворяющее равенству 
Действительно,  если векторы одинаково направлены и
если векторы одинаково направлены и  если они противоположно направлены.
если они противоположно направлены.
2. Сложение векторов.
Определение 8. Суммой двух векторов 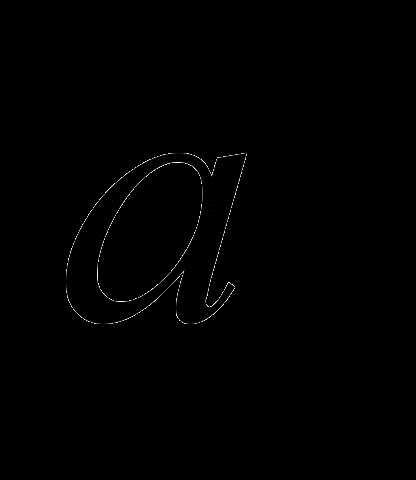
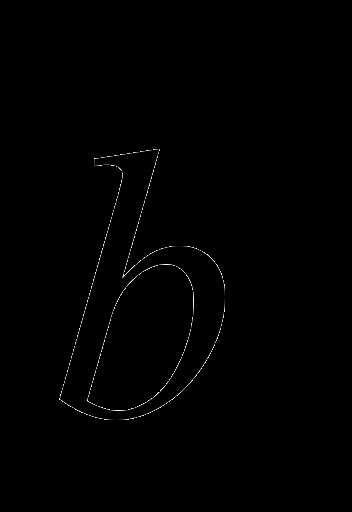 называется вектор
называется вектор  выходящий из их общего начала, который служит диагональю паралле-лограмма, сторонами которого являются векторы
выходящий из их общего начала, который служит диагональю паралле-лограмма, сторонами которого являются векторы 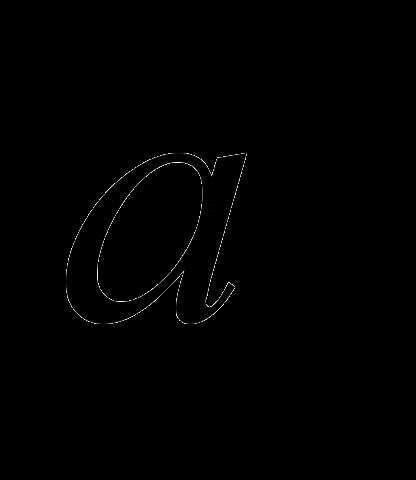 и
и  , и обозначается
, и обозначается

 или
или 
Второй способ построения суммы двух векторов легко распространить на любое число слагаемых. В результате получаем, так называемое правило многоугольника:
Чтобы построить сумму векторов, нужно в конце первого вектора построить второй, в конце второго – третий и т.д. Вектор, соединяющий начало первого с концом последнего и представляет собой искомую сумму.




С помощью рисунков легко убедиться в справедливости следующих свойств:
1. сложение коммутативно;
2. ассоциативно.
3. Вычитание векторов.
Определение 9. Вектор, коллинеарный данному вектору  , равный ему по модулю и противоположно направленный, называется противоположным вектором и обозначается
, равный ему по модулю и противоположно направленный, называется противоположным вектором и обозначается 
Определение 10. Разностью  векторов
векторов  и
и  называется сумма векторов
называется сумма векторов  и
и 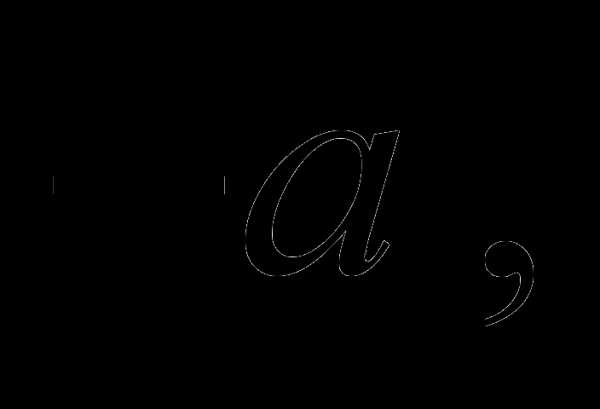 т.е.
т.е.
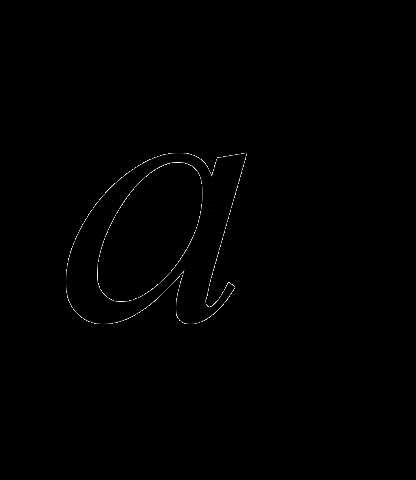
основано на построении суммы 
векторов 

Замечание 1. Из определений 6 и 8 геометрически весьма просто показать следующие свойства:
1.
2.
1.3. Декартова система координат
Зададим в пространстве три единичных взаимно перпендикулярных вектора: 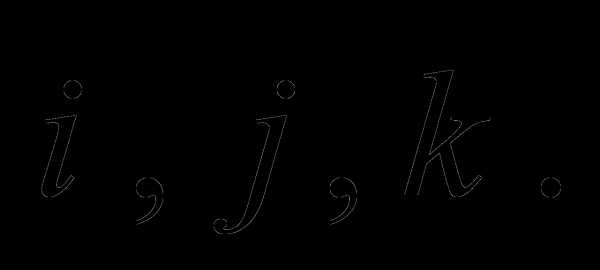 Приведём их к общему началу – точке О. Рассмотрим систему координат, направление осей: z
Приведём их к общему началу – точке О. Рассмотрим систему координат, направление осей: z
векторами  Такая система
Такая система
координат называется декартовой M
системой координат. Векторы 

называются базисом, а каждый из 
этих векторов – ортом. 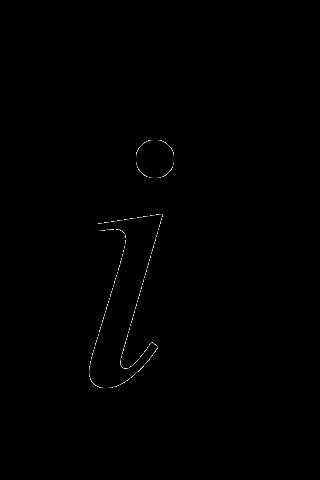
 y
y
Покажем, что если задан базис O B

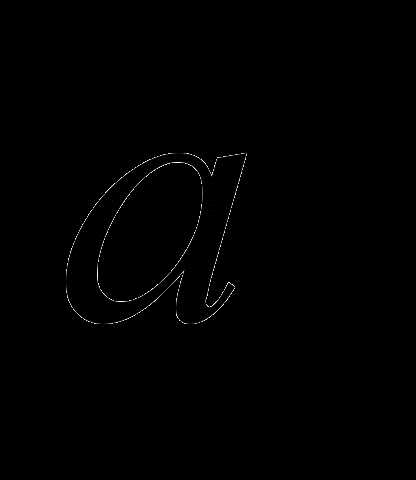 A N
A Nпространства можно единственным x
образом разложить по нему, т.е. представить в виде
(1)
Приведём вектор  к началу системы координат – точке О. Из конца вектора
к началу системы координат – точке О. Из конца вектора  точки М опустим перпендикуляр MN на плоскость Оху. Проведём из точки Nпрямые, параллельные осям координат. Построим векторы Из построения получаем
точки М опустим перпендикуляр MN на плоскость Оху. Проведём из точки Nпрямые, параллельные осям координат. Построим векторы Из построения получаем
(2)
А так как то выражение (2) примет следующий вид
(3)
В силу коллинеарности векторов 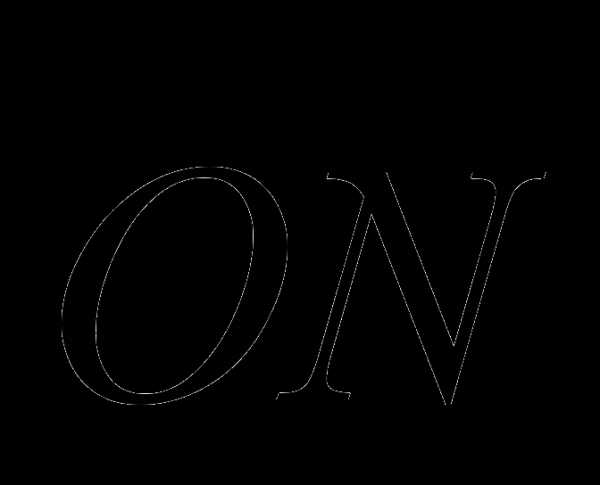
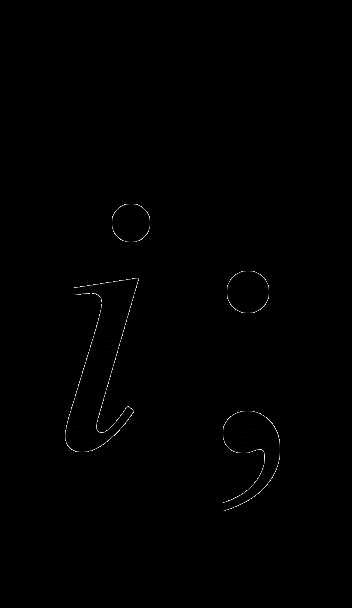
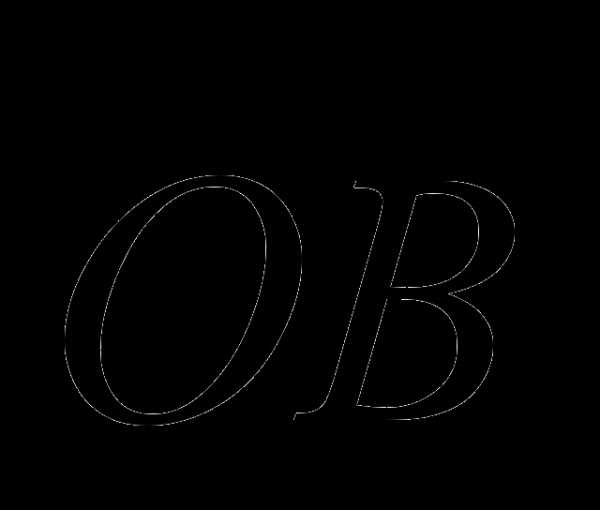 и
и 
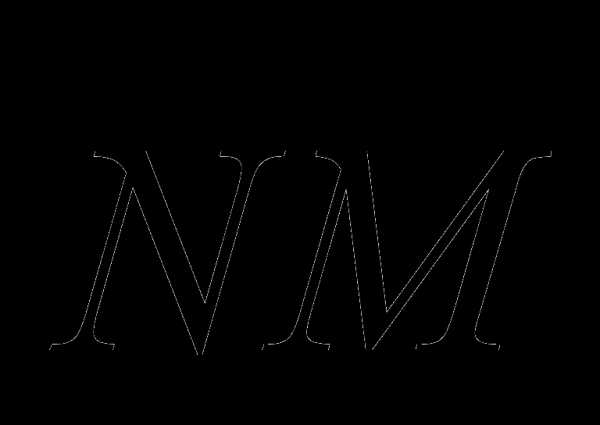 и
и  существуют такие числа
существуют такие числа 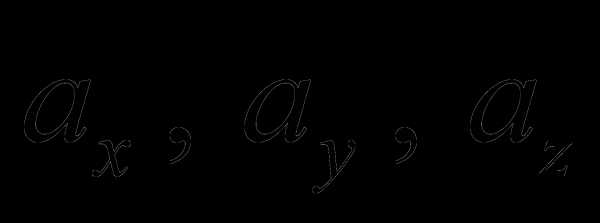 , для которых выполняется
, для которых выполняется(4)
Тогда формула (3) с учетом (4) принимает вид (1), что и требовалось доказать. Единственность разложения легко доказать от противного.
Сокращенно формула (1) записывается в виде
Определение 11. Числа 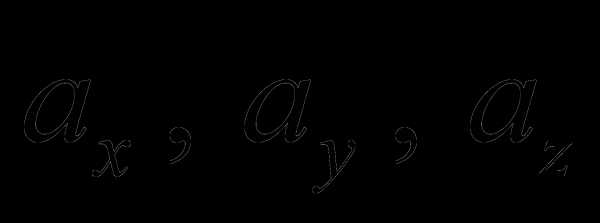 называются координатами вектора
называются координатами вектора  или его компонентами.
или его компонентами.
Используя соотношение (1), легко доказать следующие теоремы:
Теорема 1. Если и , то их сумма
Теорема 2. Если и  любое число, то произведение вектора
любое число, то произведение вектора  на это число
на это число
Следствие. Если векторы  и
и 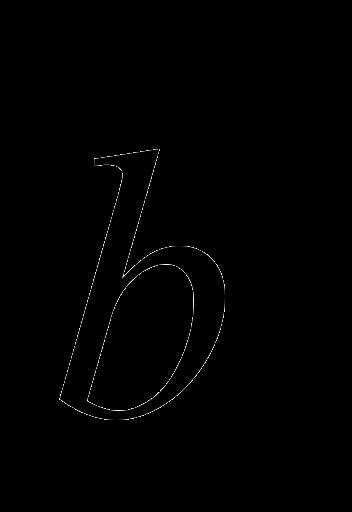 коллинеарны, то
коллинеарны, то 

 и тогда условие коллинеарности векторов имеет вид
и тогда условие коллинеарности векторов имеет вид

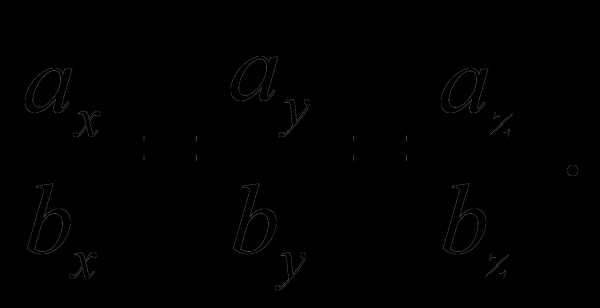 (6)
(6)
Определение 12. Радиус-вектором точки М z
называется вектор  М
М
Определение 13. Координаты радиус–вектора 
точки М называются координатами точки М
и при этом пишут 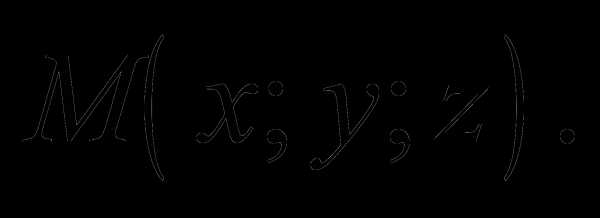 x O y
x O y
Замечание 2. Аналогично определяется система координат на плоскости Оху. Здесь образуют базис векторы 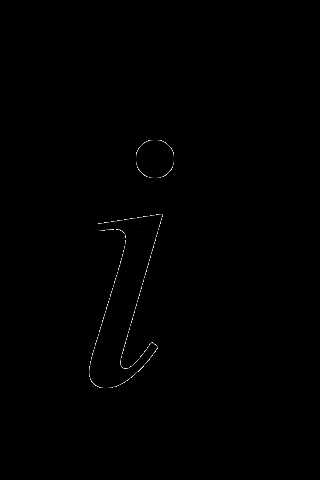 и
и  , а оси Ох и Оу. Тогда получим
, а оси Ох и Оу. Тогда получим
.
Замечание 3. Из доказательства формулы (1) следует, что геометрически координаты вектора 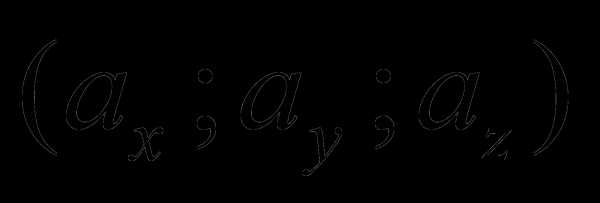 – суть его проекции на соответствующие координатные оси.
– суть его проекции на соответствующие координатные оси.
Замечание 4. Аналогично можно показать, что базис в пространстве образуют любые три некомпланарных вектора: 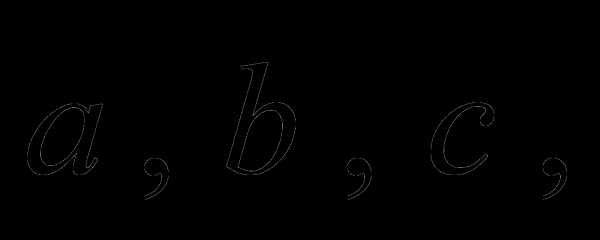 т.е. любой вектор
т.е. любой вектор  можно представить в виде
можно представить в виде
greleon.ru
Векторная алгебра
Теорема (правило Лопиталя раскрытия неопределенностей вида
$\frac{0}{0}$ или $\frac{\infty}{\infty}$).
Пусть функции $f(x)$ и $g(x)$ :
а) дифференцируемы в окрестности точки $a,$ за исключением, быть
может, самой точки $a,$ причем $g'(x)\neq 0$ в этой окрестности;
б) функции $f(x)$ и $g(x)$ являются одновременно либо бесконечно
малыми либо бесконечно большими при $x\rightarrow a;$
в) существует конечный $\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$
Тогда существует $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}$ и
выполняется равенство $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$
Если функции $f(x)$ и $g(x)$ дифференцируемы в точке $a,$
$g(a)=f(a)=0,$ $ g'(a)\neq ,0$ то $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\frac{f'(a)}{g'(a)}.$
Примеры:
1. $\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}=\lim\limits_{x\rightarrow 1}\frac{5x^4}{6x^2-1}=1.$
2. $\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$$\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{1-\frac{1}{1+x^2}}{3x^2}=\lim\limits_{x\rightarrow 0}\frac{x^2}{3x^2(1+x^2)=\frac{1}{3}.}$$
3. $\lim\limits_{x\rightarrow 1}\frac{\ln x}{\sqrt{x}}$
Имеем неопределенность вида $\frac{\infty}{\infty}.$ Применяя правило Лопиталя, получим:
$$\lim\limits_{x\rightarrow +\infty}\frac{\ln x}{\sqrt{x}}=\lim\limits_{x\rightarrow +\infty}\frac{1/x}{1/(2\sqrt{x})}=\lim\limits_{x\rightarrow +\infty}\frac{2}{\sqrt{x}}=0.$$
4. $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}.$
Имеем неопределенность вида $\frac{0}{0}.$ Замечая, что $\sin x\sim x$ при $x\rightarrow 0,$ по правилу Лопиталя находим
$\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}=\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{\cos x-\cos x+x\sin x}{3x^2}=$ $\frac{1}{3}\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}=\frac{1}{3}.$
5. $\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}.$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}=\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}.$
Пользуясь еще раз правилом Лопиталя, находим
$\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}=2\lim\limits_{x\rightarrow 1}\frac{x^9-1}{x^4-1}=2\lim\limits_{x\rightarrow 1}\frac{9x^8}{4x^3}=\frac{9}{2}.$
6. $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}},$ где $\alpha>0,$ $\beta>0.$
Пусть $k=[\alpha]+1;$ тогда $\alpha-k<0.$
Применяя правило Лопиталя $k$ раз, получаем $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}}=\lim\limits_{x\rightarrow+\infty}\frac{\alpha x^{\alpha-1}}{\beta e^{\beta x}}=…=\lim\limits_{x\rightarrow+\infty}\frac{\alpha(\alpha-1)…(\alpha-k+1)x^{\alpha-k}}{\beta^k e^{\beta x}}=0.$
7. $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}},$ где $\alpha>0,$ $\beta>0.$
Пусть $\ln x =t;$ тогда $x=e^t$ и $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}}=\lim\limits_{t\rightarrow+\infty}\frac{t^{\alpha}}{e^{\beta t}}=0$ (пример 6).
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
8. $\lim\limits_{x\rightarrow +0}x\ln x$
Преобразуя неопределенность вида $0\cdot\infty$ к виду $\frac{\infty}{\infty}$ и применяя правило Лопиталя имеем
$$\lim\limits_{x\rightarrow +0}x\ln x=\lim\limits_{x\rightarrow +0}\frac{\ln x}{1/x}=\lim\limits_{x\rightarrow +0}\frac{1/x}{-1/x^2}=\lim\limits_{x\rightarrow +0}(-x)=0.$$
9. $\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}.$
Имеем неопределенность вида $\frac{0}{0}.$ Полагая $1/x^2=t,$ получаем
$$\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}=\lim\limits_{x\rightarrow 1}\frac{t^{25}}{e^t}=0.$$
10. $\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right).$
Преобразуя неопредленность вида $\infty-\infty$ к виду $\frac{0}{0}$ и используя асимптотическую формулу $\sin x \sim x$ при $x\rightarrow 0,$ получаем
$$\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right)=\lim\limits_{x\rightarrow 0}\frac{\sin^2 x-x^2\cos^2 x}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{(\sin x+x\cos x)(\sin x-x\cos x)}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}\cdot\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}.$$
Так как
$$\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}=\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}+\lim\limits_{x\rightarrow 0}\cos x=2,$$
а $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\frac{1}{3}$ (см. пример 4), то искомый предел равен $2/3.$
mathportal.net
Векторная алгебра и аналитическая геометрия
Видео — Векторная алгебра и аналитическая геометрия
Векторы
Понятие вектора 4:24
Проекция вектора 3:12
Действия над векторами 5:56
Разложение вектора по векторам (базису) 14:54
Скалярное произведение векторов 4:23
Векторное произведение векторов 5:44
Векторное произведение векторов в координатной форме 7:08
Смешанное произведение векторов 3:59
Смешанное произведение векторов в координатной форме 5:44
Аналитическая геометрия на плоскости
Прямоугольная система координат 5:02
Полярная система координат 6:07
Простейшие задачи аналитической геометрии 7:17
Деление отрезка пополам. Середина отрезка 4:34
Деление отрезка в данном отношении 5:37
Длина отрезка. Расстояние между двумя точками 6:15
Уравнение линии 5:14
Уравнение прямой с угловым коэффициентом 5:25
Угол между прямыми 5:46
Уравнение прямой, проходящей через две точки 4:09
Общее уравнение прямой 5:52
Уравнение прямой в отрезках 3:02
Нормальное уравнение прямой 6:50
Расстояние от точки до прямой 5:36
Нахождение площади треугольника на плоскости 1:41
Окружность 5:07
Эллипс 8:00
Гипербола 8:16
Парабола 5:28
Общее уравнение кривой 2 порядка 3:46
Преобразование координат 6:59
Приведение общего уравнения кривой 2 порядка к каноническому виду 6:45
Приведение общего уравнения кривой к каноническому виду (без поворота осей) 9:25
Приведение общего уравнения кривой к каноническому виду (с поворотом осей) 11:05
Аналитическая геометрия в пространстве
Прямоугольная система координат в пространстве 6:25
www.matem96.ru
Высшая математика
42
УТВЕРЖДАЮ
Ректор университета
____________ А.В. Лагерев
«___»__________2012 г.
Методические указания и примеры
решения типовых задач по темам
«Векторная алгебра» и «Аналитическая геометрия»
для студентов I курса очной формы обучения
инженерно – технических направлений
(I семестр)
Брянск 2012
УДК 511
Высшая математика [Текс] + [Электронный ресурс]: методические указания и примеры решения типовых задач по темам: «Векторная алгебра» и «Аналитическая геометрия» для студентов I курса очной формы обучения инженерно – технических направлений (I семестр). – Брянск: БГТУ, 2012. – 36с.
Разработали: Н.А.Ольшевская, доц.
Г.Г. Цуленева, доц.
К.А. Сенько, асс.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол № 5 от 31.01.12)
Содержание
Глава 1. Векторная алгебра
Векторы. Основные понятия.
Линейные операции над векторами…………………………….….4
1.2. Скалярное произведение двух векторов..……………………………6
1.3. Векторное произведение двух векторов…………………………….8
1.4. Смешанное произведение трех векторов……………………..……10
1.5. Задачи для самостоятельного решения…………………………….12
Глава 2. Аналитическая геометрия
2.1. Прямая линия на плоскости…………………………………………13
2.2. Кривые второго порядка на плоскости……………………..………19
2.3. Плоскость в пространстве………………………………….…..……24
2.4. Прямая в пространстве. Прямая и плоскость…………….…..…….27
2.5. Задачи для самостоятельного решения……………………..………34
Список рекомендуемой литературы……………………………………..……..35
ГЛАВА 1. ВЕКТОРНАЯ АЛГЕБРА
Векторы. Основные понятия.
Линейные операции над векторами
Геометрический вектор – это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
Длиной вектора (модулем) называют длину отрезка АВ. Векторы обозначают как , а их длины.
Два вектора называются равными, если они имеют равные длины и одинаковое направление.
Вектор, начало и конец которого совпадают, называется нулевым.
Произведением вектора на некоторое число αR называется вектор, длина которого равна длине вектора , умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора, если α>0, и противоположно ему, если α<0.
Суммой нескольких векторов называется вектор, проведенный из начала первого вектора в конец последнего при условии, что начало каждого последующего вектора совмещается с концом предыдущего.
Проекцией вектора на ось Ох называется число, равное длине вектора , умноженной на косинус угла между вектороми положительным направлением оси Ох.
Радиусом-вектором точки М называется вектор соединяющий начало координат с этой точкой.
Единичные векторы координатных осей называются ортами.
Углы α, β, γ между вектором и положительными направлениями осей координат называются направляющими, при этом для векторас координатами Х,Y, Z
причем =1.
Если векторы и заданы своими координатами как и , то координаты векторабудут равны: {ma1 +nb1, ma2 +nb2, ma3 +nb3}, а вектор ma1 +nb1)+(ma2 +nb2)+(ma3 +nb3).
studfiles.net
Высшая математикаВекторыОпределение
Сложение векторовСумма нескольких векторовВычитание векторовУмножение вектора на числоПример
Проекция вектора на осьКоординатные векторыРазложение вектора на составляющиеФормула модуля вектораКоординаты вектораСкалярное произведение векторовОпределение
Физический смысл скалярного произведения
Выражение скалярного произведения через координаты перемножаемых векторов
Свойства скалярного произведенияПримерПример
Векторное произведениеОпределение
Обозначение векторного произведения векторовПонятие «правой» тройки векторов
Векторные произведения координатных векторовВыражение векторного произведения через координаты перемножаемых векторовПример
Свойства векторного произведенияПримерНаправляющие косинусы вектораФормула связи направляющих косинусовЕдиничный вектор
Координаты единичного вектораПример
Физический смысл векторного произведенияУсловия коллинеарности двух векторовКомпланарные векторы
Условия компланарности трёх векторовКоллинеарные векторы
Условие коллинеарности двух векторовНекоторые кривыеПоверхности второго порядка |
dok.opredelim.com
ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ — Лекции по высшей математике
Лекции по высшей математикеДоступные файлы (30):
n1.doc
ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ
Аналитическая геометрия изучает геометрические образы (точки, прямые, плоскости, поверхности и т.д.) при помощи аналитического метода. В основе этого метода лежит метод координат Рене Декарта (французский математик 1596-1650), позволяющий ввести соответствия между основными понятиями геометрии (точки, прямые, плоскости) и упорядоченными тройками вещественных чисел. Изучение свойств и взаимного расположения геометрических образов в аналитической геометрии сводится к изучению описывающих эти образы уравнений с привлечением методов алгебры и математического анализа.
I. Вектор, геометрическое определение вектора. Равные векторы.
Пусть на некоторой прямой заданы две точки A и B . Тем самым выделен отрезок AB этой прямой с концами в точках A и B.
Можно считать, что точка A — начало отрезка, B — конец. Тогда мы зададим так называемый направленный отрезок, определяемый упорядоченной парой точек.
Определение . Направленный отрезок (упорядоченную пару точек) называют вектором. Вектор обозначается или . Если точки A и B совпадают, то говорят, что вектор нулевой или нуль-вектор .
Расстояние между началом и концом вектора называется его длиной или модулем и обозначается .
В
екторы называются коллинеарными, если они имеют общую параллельную прямую. При совмещении начал коллинеарных векторов они оказываются лежащими на одной прямой.
В
екторы называются компланарными, если они параллельны одной и той же плоскости. При совмещении начал компланарных векторов они оказываются лежащими в одной плоскости.
Теперь можно ввести следующее определение: два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
, если
, хотя но
Из определения равенства векторов следует, что каждый вектор можно перенести в любое место параллельно самому себе и не изменить его. Тем самым мы ввели так называемый свободный вектор, задать который — значит задать его модуль и направление. Многие физические величины характеризуются не только числовым значением, но и направлением, и, следовательно, являются векторными (сила, скорость, перемещение, магнитная индукция…).
II. Линейные операции над векторами, их свойства.
Понятие о линейном пространстве.
К линейным операциям над векторами относятся сложение векторов и умножение вектора на скаляр.
Сложение двух векторов выполняется по правилу параллелограмма: сумма двух векторов представляет собой диагональ параллелограмма, построенного на равных им векторах.
Сумма нескольких векторов определяется как вектор, замыкающий ломаную линию, звеньями которой служат векторы-слагаемые, и направленный из начала первого вектора в конец последнего.
Определение: произведением вектора на вещественное число называется
такой вектор , что 1)
2) вектор коллинеарен ,
3) векторы и направлены одинаково,
если ,
и противоположно, если :
,если , ,если .
Вектор называется противоположным вектору . Сумма двух противоположных векторов равна нулевому вектору: .
Вычитание векторов — операция, обратная сложению:
Перечислим свойства введенных нами линейных операций:
1
) коммутативность сложения: ;
2) ассоциативность сложения: ;
3) существование нуль-вектора: ;
4) существование противоположного вектора: ;
5) дистрибутивность сложения по отношению к умножению на число:
6) дистрибутивность сложения:
A B C D E
7) ассоциативность умножения: т.к.
8) существование единицы: это следует из определения
операции умножения.
Пространство, для элементов которого вводятся операции сложения и умножения на число, обладающие свойствами (1)-(8), называют линейным (векторным) пространством. Элементы линейного пространства обычно называют векторами.
III. Разложение вектора по базису. Координаты вектора.
Пусть заданы векторы и числа Составим комбинацию из этих векторов, используя только введенные линейные комбинации сложения и умножения вектора на число. В самом общем случае она имеет вид: . Такие комбинации называются линейными комбинациями векторов , а числа — коэффициентами линейной комбинации.
Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.
Пусть дан ненулевой вектор . Покажем, что любой коллинеарный ему вектор может быть представлен в виде единственным образом.
По определению операции умножения вектора на число векторы и коллинеарны, следовательно, коллинеарны и векторы и . Одинаковое направление векторов и обеспечивается выбором знака числа . Наконец, из равенства модулей равных векторов следует, что . Единственность представления следует из того, что при умножении вектора на другое число получается новый вектор: при .
Теорема 1. Любой вектор на плоскости может быть разложен по двум неколлинеарным векторам и единственным образом.
Доказательство: В общем случае отложим все три вектора из общей точки О. Из конца вектора (точки А) проведем прямые АР и AQ, параллельные векторам и . Тогда по правилу параллелограмма
.
Вектор коллениарен вектору и, следовательно, единственным образом может быть представлен в виде . Вектор коллинеарен вектору , поэтому . Тогда — единственное разложение вектора по векторам и .
Неколлинеарные векторы и , взятые в определенном порядке, называются базисом на плоскости, а коэффициенты линейной комбинации 1 и 2 — координатами вектора в базисе и .
Т
.
еорема2: любой вектор единственным образом раскладывается по трем фиксированным некомпланарным векторам:
Некомпланарные векторы образуют базис пространства. Коэффициенты разложения называют координатами вектора в базисе .
Таким образом, в пространстве с выбранным базисом нам удалось каждому вектору поставить в соответствие тройку чисел — его координат. Теперь при выполнении введенных линейных операций над векторами можно заменить геометрические построения аналитическими выражениями.
Пусть
тогда
и
Таким образом, при умножении вектора на число все его координаты умножаются на это число, а при сложении векторов складываются их соответствующие координаты, если они определены относительно одного и того же базиса.
IV. Линейная зависимость векторов. Размерность линейного пространства.
Запишем линейную комбинацию векторов Она называется тривиальной, если все ее коэффициенты одновременно равны нулю, то есть , и нетривиальной, если хотя бы один из коэффициентов отличен от нуля.
Определение: векторы называют линейно зависимыми, если можно найти их нетривиальную комбинацию, равную нулю:
при .
Определение: если для векторов обращается в нуль только их тривиальная комбинация, то такие векторы называют линейно независимыми:
при .
Векторы линейно зависимы, если хотя бы один из них можно представить как линейную комбинацию остальных. Пусть , тогда
Тогда на основании доказанных выше теорем оказывается, что линейно зависимыми являются любые два коллинеарных вектора (), любые три компланарных вектора () и любые четыре вектора в пространстве (). В свою очередь линейно независимыми всегда являются базисные векторы, т.е. два неколлинеарных вектора на плоскости и три некомпланарных вектора в пространстве.
Определение: количество векторов, образующих базис линейного пространства, называют размерностью этого пространства.
Размерность определяется наибольшим числом линейно независимых векторов пространства. Линейное пространство, имеющее размерность n, принято обозначать .
V. Системы координат.
Определение: декартовой системой координат называются совокупность точки и базиса.
Точка О называется началом координат,
Ox,Oy,Oz — координатными осями,
Oxy,Oyz,Oxz — координатными плоскостями.
Декартова система координат, базисные векторы которой взаимно перпендикулярны и имеют единичные длины, называется декартовой прямоугольной системой, а ее базис – ортонормированным.
Координатами точки А в выбранной cистеме координат называются координаты радиус-вектора этой точки в этой системе координат.
Если заданы координаты точек и , то можно найти выражение для координат вектора .
Из рисунка 6 следует, что , тогда . Если , то — координаты вектора .
На практике пользуются и другими системами координат, например, косоугольной декартовой, полярной, цилиндрической, сферической и др.
perviydoc.ru
