Как определить функцию – Функции. Основные виды, графики, способы задания

Как определить функцию системы

До сих пор мы говорили так, будто функция любой системы управления поведением настолько очевидна, что ее можно воспринимать, как нечто само собой разумеющееся. Действительно, ни у ко не возникает вопрос, в чем состоит функция потребления пищи, высиживания яиц или миграции. Тем не менее имеется ряд поведенческих систем, функции которых, как давно признано, остаются неясными. Одна из известных систем такого рода — это территориальное поведение многих видов птиц и млекопитающих. Никто не сомневается, что такое поведение попадает в общую категорию, называемую нами инстинктивным поведением, однако какое именно преимущество (или преимущества) оно дает биологическому виду часто остается неясным. В современной биологической науке утвердилось мнение, что любое инстинктивное поведение обладает своей специфической функцией (или функциями), способствующей выживанию вида. (Несмотря на разные точки зрения относительно сущности данной функции.)

Задача точного определения функции какого-то компонента инстинктивного поведения может быть достаточно трудной. Во-первых, необходимо установить, что в зоне эволюционной адаптированности вида особи, обладающие таким поведением, имеют более многочисленное потомство, чем те, у которых оно отсутствует, и, во-вторых, должна быть раскрыта причина такого поведения. Лучше всего необходимое исследование проводить в естественных условиях. Его метод связан с экспериментальным вмешательством: необходимо сделать так, чтобы одни представители вида не могли бы вести себя привычным образом, а затем сравнить успешность их выживания и размножения с такими же данными об особях, в жизнь которых не вмешивались. В последние годы Тинберген (Tinbergen, 1963) проводил такие эксперименты. Он исследовал некоторые особенности поведения чаек, связанного с выведением птенцов. Без таких экспериментов с интересующим нас (или, по крайней мере, с близким к нему) видом любая дискуссия о том, какой именно из многих обычно получаемых результатов определенного компонента инстинктивного поведения является его функциональным результатом, будет бесплодной и умозрительной.

В гл. 12 утверждается, во-первых, что поведение маленького ребенка, направленное на то, чтобы находиться рядом с матерью (оно называется поведением привязанности), является примером инстинктивного поведения и, во-вторых, что его функция обсуждалась совершенно недостаточно и все еще остается спорной. При этом выдвигается гипотеза, которая до настоящего момента мало рассматривалась в кругах клиницистов.

Проблемы терминологии

Теперь, когда мы в основных чертах обрисовали альтернативную теорию инстинктивного поведения, пора кратко обсудить полезность или, напротив, бесполезность некоторых традиционно используемых понятий.

Во вступлении к гл. 3 отмечалось, что пока слово «инстинктивный» используется описательно, в качестве прилагательного, оно приемлемо и полезно, но как только мы обращаемся к существительному «инстинкт», возникают трудности. Рассмотрим, почему так происходит.

Выдвигаемая нами теория инстинктивного поведения подразумевает, что такое поведение является результатом активации особых условиях внешней среды систем управления поведением, которые интегрированы или в цепи, или в иерархии, или в сочетания того и другого; и что любая система управления поведением и любой комплекс таких систем устроены так, что их активация, как правило, приводит к достижению результата, имеющего значение для выживания. Возникает вопрос, к чему же конкретно; относится субстантивное существительное «инстинкт»? Должно ли оно относиться к самому поведению? Или к системе, управляющей поведением? Или к причинным условиям, которые активизируют систему управления поведением? Или к его прогнозируемому результату? Или, может быть, к функции, которую оно выполняет?

Дело в том, что известные исследователи использовали термин «инстинкт» во всех этих значениях. С одной стороны, он употреблялся в довольно узком значении — применительно к паттернам фиксированного (в большей или меньшей степени) действия, таким, как «поворачивание головы», и к таким движениям, как схватывание добычи, т.е. к конечному звену целой цепочки движений, образующих какую-либо форму инстинктивного поведения. С другой стороны, этот термин использовался в очень широком значении — применительно к силам, которые рассматриваются как причинные факторы и связаны с такими общими состояниями, как жизнь или смерть. Иногда этим термином обозначают прогнозируемый результат последовательных реакций, образующих инстинктивное поведение, например, «инстинкт сооружения гнезда» и «половой инстинкт», или же его относят к биологической функции — «инстинкт воспроизведения». Иногда этот термин используется применительно к эмоции, которая сопровождает поведение, например «инстинкт страха».

Ясно, что такое неупорядоченное использование термина приводит только к путанице. Возникает вопрос: нельзя ли прийти к какому-то общепринятому употреблению этого термина. Существуют две веские причины, по которым это невозможно. Во-первых, термину, который использовался так широко, нелегко дать новое определение и начать употреблять в точном соответствии с новым значением. Во-вторых, из-за интегративного характера систем управления поведением любого уровня сложности чрезвычайно трудно провести границу и решить, что все комплексы управляющих систем, находящиеся по сложности ниже нее, следует называть инстинктами, а все комплексы систем, находящиеся выше нее, так называть не следует. Это было бы похоже на разделение промышленных концернов по уровню их организационной сложности на две группы и присвоение менее сложным специального названия. Нет необходимости подчеркивать трудность этой задачи, но главный вопрос в том, будет ли от этого польза?

Выделение неких управляющих систем поведения — по каким бы критериям оно ни проводилось — и обозначение их термином «инстинкт» не достигло бы никакой практической цели. А кроме того, оно закрепило бы широко распространенную ошибку, связанную с предположением, будто системы, входящие в единый комплекс, имеют общие причины, которые можно представить в качестве «влечений».

В гл. 6 было описано взаимодействие различных факторов, активизирующих управляющие системы, ведущие к сооружению гнезда у канареек. Это исследование также может проиллюстрировать положение, которое мы будем сейчас обсуждать. В сооружении гнезда канарейками выделяются следующие действия: сбор материала для устройства гнезда; доставка материала в гнездо; строительство гнезда (последним птица занимается, сидя в самом гнезде). Поскольку все эти действия варьируются более или менее согласованно, можно было бы посчитать, что ими управляет некое «влечение к сооружению гнезда». Анализ факторов, приводящих в действие три названных компонента активности, показывает, что они имеют общие причинные факторы: все компоненты находятся под влиянием уровня эстрогенов и тормозятся раздражителями, находящимися в гнезде. Тем не менее соотношение между тремя компонентами активности подвержено и другим воздействиям: у каждого имеются свои специфические факторы, а последовательность их выполнения, по-видимому, соблюдается благодаря эффекту самоподавления при завершении каждого вида деятельности. Поэтому представление о неком едином влечении к сооружению гнезда совершенно неадекватно. То же самое было бы и в случае, если бы мы утверждали, что каждому компоненту деятельности по сооружению гнезда соответствует отдельное влечение, поскольку каждое действие можно разложить на отдельные составляющие его движения, варьирующиеся относительно независимо друг от друга.

На самом деле, чем лучше мы начинаем понимать причинные факторы инстинктивного поведения, тем менее состоятельной становится концепция влечения. Пока побудительные причины действия неизвестны, легко предположить, что какая-то особая сила движет поведением, причем не только инициирует его, но и таинственным образом направляет по правильному пути. Но если мы правы, считая, что поведение является результатом активации систем управления поведением и что активация вызвана описанными причинами, тайна раскрывается и необходимость в постулировании влечений отпадает. Инженерам не нужно постулировать специальное «влечение к уничтожению самолетов», чтобы объяснить действие самонаводящегося орудия, а физиологам — «влечение к кровоснабжению» для объяснения деятельности сердечно-сосудистой системы.

Поэтому в нашем дальнейшем изложении не используется ни понятие «инстинкт» (как отдельная форма поведения), ни понятие; «влечение».

Описательный термин «инстинктивное поведение» может использоваться, однако, применительно к такому поведению, которое в среде эволюционной адаптированности дает важные для выживания вида результаты и управляется системами, в этой среде обычно довольно стабильными. В то же время нужно признать, что даже если слово «инстинктивный» используется исключительно в качестве прилагательного, оно несет две опасности. Первая связана с тем, что может возникать предположение, будто все виды инстинктивного поведения управляются системами только одного типа. Вторая опасность — создание ложной дихотомии между инстинктивным поведением и всеми другими видами поведения. На самом деле поведение, традиционно описываемое как инстинктивное, управляется множеством систем различных типов, и эти системы образуют непрерывные ряды — от самых стабильных до самых лабильных систем и от наиболее необходимых для выживания вида систем до вносящих в него минимальный вклад. Поэтому между тем, что мы называем инстинктивным поведением, и тем, что так называть нельзя, четкая граница может отсутствовать.

В некоторых психоаналитических теориях (Schur, 1960а, 1960b) прилагательные «инстинктивный» (instinctive) и «инстинктуальный» (instinctual) используются в разных значениях: термин «инстинктивный» сохраняется за поведением, которое в данной работе также называется инстинктивным, а термин «инстинктуальный» применяется по отношению к постулируемой автором «психической энергии влечения», которая, как он полагает, разряжается посредством инстинктивного поведения. Поскольку в теории, выдвигаемой в нашей работе, никакой психической энергии влечения не предполагается, прилагательное «инстинктуальный» не используется совсем

1. Прилагательное «инстинктивный» используется как в отношении такого рода поведения, так и в отношении поведенческих систем, управляющих этим поведением.

__________

¹В опубликованном ранее исследовании по проблеме страха и печали термин «системы инстинктуальных реакций» по существу использовался применительно к системам управления, отвечающим за инстинктивное поведение. По изложенным выше причинам в переработанных вариантах этого материала (он будет включен в том II и том III трилогии) терминология была изменена.

Также требует рассмотрения ряд других терминов, используемых при обсуждении инстинктивного поведения и психопатологии. К ним относятся такие термины, как «потребность», «желание», «цель», «намерение» и многие другие. Возникает вопрос: какое место занимает каждый из них в данной схеме и как они соотносятся с такими понятиями, как «прогнозируемый результат», «установочная цель» и «функциональный результат»?

Во избежание пристрастного отношения к какой-либо определенной теории инстинктивного поведения, а также для указания на явно целевой характер систем управления поведением иногда используют термин «потребность» или «система потребности». Однако это неправильно, во-первых, потому, что этим термином часто пользуются для обозначения того, что необходимо для выживания, например «витальная потребность». Во-вторых, он может увести в сферу телеологического рассуждения. Рассмотрим эти трудности более внимательно.

В этой главе подчеркивалось, что наличие у животного определенного вида какой-либо стабильной (в отношении условий внешней среды) системы управления поведением объясняется тем, что деятельность этой системы обычно приводит к результату, имеющему значение для выживания вида. Результатом активности системы, ответственной за пищевое поведение, как правило, является прием пищи. Системы управления, ответственные за поведение спаривания, обычно в качестве результата приводят к воспроизведению потомства. Поскольку деятельность этих систем столь очевидным образом служит удовлетворению биологических потребностей, почему бы не назвать их «системами потребностей» («need systems»)?

Однако имеется, по крайней мере, три веские причины не делать это. Во-первых, в каждом конкретном случае деятельность системы управления поведением, о которой идет речь, может иметь совершенно другие результаты. Например, система, прямо связанная с потреблением пищи, может в качестве результата приводить к сосанию большого пальца или трубки¹. В другом случае система, прямо направленная на спаривание, может в качестве основного результата приводить к сексуальной активности, направленной на фетиш или на представителя того же пола. В этих примерах деятельность системы не представляет никакой ценности с точки зрения выживания. Поэтому назвать такую систему системой потребности нельзя — это вызовет путаницу, которая лишь усилится, если (ради ее избежания) станут постулировать новые потребности, например потребность сосать палец. Во-вторых, как уже отмечалось, существует ряд видоспецифичных систем управления поведением, биологические функции которых еще неясны. Это обстоятельство маскируется, если каждую систему управления поведением называть системой потребности, поскольку термин «потребность» обычно подразумевает, что полезность системы самоочевидна. И в-третьих, термин «система потребности» может легко привести к предположению, что потребность способна выступать в качестве причины активации системы, — давнее заблуждение телеологии.

____________

¹Однако в некоторых случаях сосание может быть по своей сути не связано с питанием; см. гл. 13 и 14.

При правильном использовании термин «потребность» должен ограничиться обозначением того, что необходимо для выживания вида. Можно сказать, что для сохранения вида животному необходима пища, тепло, место для выращивания потомства, самец или самка и так далее. Очевидно, ни одна из этих потребностей не является системой управления поведением, и ни одна из них не вызывает активацию системы управления поведением. В то же время функция многих систем управления поведением состоит в удовлетворении той или иной из этих потребностей; именно ради реализации этих функций, необходимых для выживания вида, и происходила эволюция систем управления конкретными формами поведения. Потребности, следовательно, не являются причинами инстинктивного поведения. Их задача — определять те функции, которые должна выполнять система управления поведением. Таким образом, они как бы заключают в себе требования естественного отбора, в условиях которого происходит эволюция систем управления поведением.

Так же как потребности не являются причинами инстинктивного поведения, так же ими не являются желания (wishes) и хотения (desires). Термины «желание» и «хотение» относятся к осознанию человеком установочной цели какой-либо системы управления поведением или комплекса таких систем, которые уже находятся в состоянии активации либо, по крайней мере, готовы к действию. Высказывание «У меня есть желание поесть» или «Мне хочется есть» означает активацию комплекса систем управления поведением, установочной целью которых является прием пищи (возможно, только его начальная стадия), а также то, что человек ее осознает. Обычно подобные высказывания верны, но психоаналитики знают, что так бывает далеко не всегда. На самом деле субъект может неправильно идентифицировать установочную цель системы управления поведением, находящейся в активном состоянии. В свою очередь ошибочная идентификация сама может быть результатом вмешательства со стороны действующей системы, имеющей установочную цель, несовместимую с первой. Это приводит нас к понятию бессознательного желания.

Когда мы говорим, что желание неосознанно, это означает, что у человека, о котором идет речь, система управления поведением или комплекс систем, имеющих такую-то установочную цель, находятся в состоянии активации, но сам человек об этом не знает.

В то время как термин «желание» относится к установочной цели системы управления поведением, термин «намерение» обычно относится к какой-то стадии на пути к достижению установочной цели. Когда я говорю, что намеренсделать то-то и то-то, это обычно означает, что «то-то и то-то» является частью плана, направляющего в данный момент мое поведение (это положение разработано Миллером, Галантером и Прибрамом [Miller, Galanter, Pribram, I960]).

Существует целый ряд различных терминов для обозначения того, что в этой главе называется «прогнозируемым результатом» и его частным случаем — «установочной целью». Сюда входят понятия «цель как намерение» (purpose), «цель как стремление» (aim) и просто «цель» (goal). О недостатках термина «цель» мы уже говорили (см. гл. 5).

С употреблением терминов «цель-намерение» и «цель-стремление» имеются определенные трудности, так как каждый из них несет в себе оттенок телеологического представления о причинной обусловленности. Более серьезные трудности связаны с тем, что их привычное использование не позволяет провести различие между прогнозируемым результатом системы и ее функцией — возникает неустранимая путаница. По этой причине ни тот, ни другой термин в этой книге не используются. Интересно, что хотя английское слово «aim» обычно применяется в обоих этих значениях, Фрейд почувствовал при его использовании некоторые трудности, когда формулировал определение цели инстинкта. Например, в своей работе «Влечения и судьбы влечений» (Freud, 1915а) он признавал фундаментальное различие между завершающими стимулами, с одной стороны, и функцией, с другой стороны, и использовал термин «цель-стремление» только в том значении, которое в терминах; принятых в данной работе, передается как «достижение завершающих условий рассматриваемой системы управления поведением».

Для обозначения того, что в нашей работе называется прогнозируемым результатом или установочной целью, в литературе вводились специальные термины. Термин «основное условие» (focal condition) Зоммерхоффа — очень близкий моему термину «прогнозируемый результат», хотя он может не распространяться на прогнозируемый результат наиболее простых форм поведения, например перекатывание яйца. Немецкий термин «золльверт» (sollwert), введенный Миттельштадтом и используемый Хайндом, обозначает определенного вида установочные цели, т.е. состояние, которое» «должно быть», или состояние, которого должна достигнуть и/или поддерживать система. Один недостаток этого термина может быть в том, что он был введен применительно к установочным целям, для достижения которых требуется учет характеристик только одного вида, например, положение конечности или пение ноты, их; невозможно так легко применить к более сложным установочным целям, для достижения которых необходим учет двух и более характеристик. Другой возможный недостаток термина «золльверта» в том, что состояние, которое «должно быть», может ошибочно быть принято за норму, которая способствует выживанию. На самом деле, как уже неоднократно подчеркивалось, установочная цель (или золльверт системы управления поведением), у каждой отдельной особи может быть атипичной и даже неблагоприятной для выживания.

Иногда нами использовалось прилагательное «целевой» для описания системы, обладающей установочной целью. Однако здесь существует опасность истолкования его в духе телеологической причинной обусловленности (еще большая опасность возникает в отношении близкого ему по значению прилагательного «целенаправленный» (purposeful). Питтендрай (Pittendrigh, 1958) противопоставил этому термин «телеономический». Его можно использовать для обозначения любой живой или механической системы, которая, активизируясь в зоне адаптированности, достигает прогнозируемого результата. По этой причине все системы управления поведением, о которых мы ведем речь, можно назвать телеономическими.

Возвращаясь еще раз к понятию «установочная цель», нужно заметить, что установочная цель системы управления поведением (как и в случае любой другой системы управления) может быть двух основных типов. Первый — это поддержание постоянного значения некой характеристики. Например, некоторые простейшие организмы снабжены системами управления поведения, имеющими в качестве установочной цели задачу удерживать организм в среде, температура которой не выходит за узкие рамки допустимого диапазона. Задача таких систем управления поведением никогда не снимается с повестки дня: у нее нет высшей точки их деятельности и нет драмы. Это однообразная рутинная задача. Другим типом установочной цели является акт, ограниченный по времени осуществления и служащий финальным аккордом деятельности. Яркими примерами этого типа являются сексуальное совокупление и перехват добычи. Для некоторых систем управления поведением характерно расположение установочной цели между этими крайними точками.

В отношении человека явно прослеживалась тенденция придавать неоправданно большое значение системам управления поведением, у которых имеются конечные установочные цели (например, оргазм), и слишком мало уделять внимания системам, имеющим установочные цели постоянного характера (например, близость как нахождение рядом или в пределах досягаемости какого-то объекта во внешней среде). Поведение привязанности может рассматриваться как результат деятельности систем управления поведением, имеющих постоянную установочную цель, особенностью которой служат определенного рода отношения с другим индивидом.

studfiles.net

Как проверить функцию на четность и нечетность 🚩 как исследовать функцию на четность и нечетность 🚩 Математика

20 февраля 2012

Автор КакПросто!

Большую часть школьной программы математики занимает исследование функций, в частности, проверка на четность и нечетность. Этот метод является важной составляющей процесса изучения характера поведения функции и построения ее графика.

Статьи по теме:

Инструкция

Свойства четности и нечетности функции определяется исходя из влияния знака аргумента на ее значение. Это влияние отображается на графике функции в определенной симметрии. Иными словами, выполняется свойство четности, если f(-x) = f(x), т.е. знак аргумента не влияет на значение функции, и нечетности, если справедливо равенство f(-x) = -f(x).

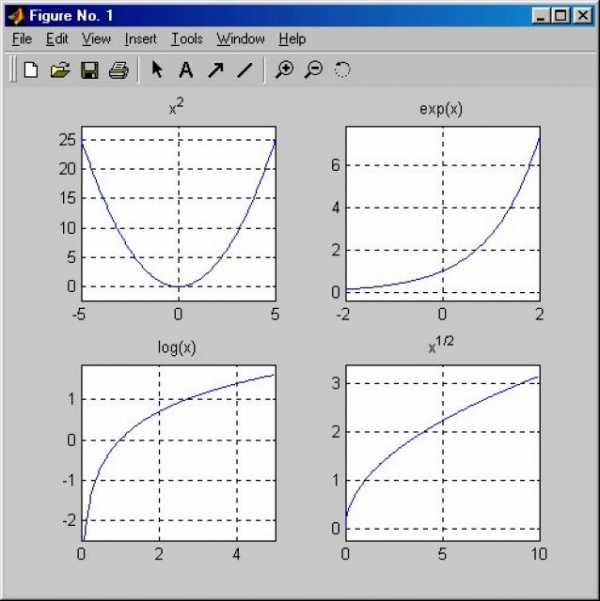
Нечетная функция графически выглядит симметричной относительно точки пересечения координатных осей, четная – относительно оси ординат. Примером четной функции может служить парабола x², нечетной – f = x³.

Пример № 1Исследовать на четность функцию x²/(4·x² — 1).Решение:Подставьте в данную функцию –x вместо x. Вы увидите, что знак функции не изменится, поскольку аргумент в обоих случаях присутствует в четной степени, которая нейтрализует отрицательный знак. Следовательно, исследуемая функция является четной.

Пример № 2Проверить функцию на четность и нечетность: f = -x² + 5·x.Решение:Как и в предыдущем примере, подставьте –x вместо x: f(-x) = -x² – 5·x. Очевидно, что f(x) ≠ f(-x) и f(-x) ≠ -f(x), следовательно, функция не обладает свойствами ни четности, ни нечетности. Такая функция называется индифферентной или функцией общего вида. Исследовать функцию на четность и нечетность можно также наглядным образом при построении графика или нахождении области определения функции. В первом примере областью определения является множество x ∈ (-∞; 1/2) ∪ (1/2; +∞). График функции симметричен относительно оси Oy, значит, функция четная. В курсе математики сначала изучают свойства элементарных функций, а затем полученные знания переносят на исследование более сложных функций. Элементарными являются степенные функции с целым показателем, показательные вида a^x при a>0, логарифмические и тригонометрические функции.

Чётные и нечётные функции – это числовые функции, области определения которых (и в первом, и во втором случае) симметричны относительно системы координат. Как же определить, какая из двух представленных числовых функций является чётной?

Вам понадобится

• лист бумаги, функция, ручка

Инструкция

Для того чтобы определить чётную функцию, прежде всего запомните её определение. Функцию f (x) можно назвать чётной, если для любого значения х (икс) из области определения выполняются оба равенства: а) -x € D;
б) f (-x) = f (x). Запомните, что если при противоположных значениях x (икс) значения y (игрек) равны, то исследуемая функция является чётной. Рассмотрите пример чётной функции. Y = x?. В этом случае при значении x = -3, y = 9, и при противоположном значении x = 3 y = 9. Обратите внимание, данный пример доказывает, что при противоположных значениях x (икс) (3 и -3) значения y (игрек) равны. Обратите внимание, что на всей области определения график чётной функции симметричен оси OY, в то время как график нечётной функции на все области определения симметричен относительно начала координат. Простейшим примером чётной функции служат функции y = cos x; y = ?x?; y = x? + ?x?.

Если точка (a; b) принадлежит графику чётной функции, то и симметричная ей относительно оси ординат точка
(-a; b) также принадлежит данному графику, из чего следует, что график чётной функции симметричен относительно оси ординат.

Помните, что не каждая функция обязательно является либо чётной, либо нечётной. Некоторые из функций могут быть суммой чётной и нечётной функций (примером может служить функция f (x) = 0).

При исследований функции на чётность, запомните и оперируйте следующими утверждениями: а) сумма чётных (нечётных) функций также является чётной (нечётной) функцией; б) произведение двух чётных или нечётных фунций является чётной функцией; в) произведение нечётной и чётной функций является нечётной функцией; г) если функция f чётна (либо нечётна), то и функция 1/f также является чётной (либо нечётной).

Функция называется чётной, если при изменении знака аргумента значение функции остаётся неизменным. f (x) = f (-x). Используйте этот простой способ для определения чётности функции: если значение останется неизменным при умножении на -1, то функция – чётная.

Видео по теме

Исследование функции на четность или нечетность — один из шагов общего алгоритма исследования функции, необходимого для построения графика функции и изучения её свойств. В этом шаге необходимо определить, является ли функция четной или нечетной. Если про функцию нельзя сказать, что она является четной или нечетной, то говорят, что это функция общего вида.

Инструкция

Запишите функцию в виде зависимости y=y(x). Например, y=x+5. Подставьте вместо аргумента x аргумент (-x) и посмотрите, что получилось в итоге. Сравните с изначальной функцией y(x). Если y(-x)=y(x), имеем четную функцию. Если y(-x)=-y(x), имеем нечетную функцию. Если y(-x) не равняется y(x) и не равняется -y(x), имеем функцию общего вида. Запишите вывод к данному шагу исследования функции. Возможные варианты вывода:y(x) — четная функция,y(x) — нечетная функция,y(x) — функция общего вида.

Переходите к следующему шагу исследования функции, используя стандартный алгоритм.

Исследование функции на четность и нечетность помогает строить график функции и изучать характер ее поведения. Для этого исследования необходимо сравнить данную функцию, записанную для аргумента «х» и для аргумента «-х».

Инструкция

Запишите функцию, исследование над которой необходимо провести, в виде y=y(x).

Замените аргумент функции на «-х». Подставьте этот аргумент в функциональное выражение.

Упростите выражение.

Таким образом, вы получили одну и ту же функцию, записанную для аргументов «х» и «-х». Посмотрите на две эти записи.
Если y(-x)=y(x), то это четная функция.
Если y(-x)=-y(x), то это нечетная функция.
Если же про функцию нельзя сказать, что y(-x)=y(x) или y(-x)=-y(x), то по свойству четности это функция общего вида. То есть, она не является ни четной, ни нечетной.

Запишите сделанные вами выводы. Теперь вы можете их использовать в построении графика функции или же в дальнейшем аналитическом исследовании свойств функции.

Говорить о четности и нечетности функции можно также и в том случае, когда уже задан график функции. Например, график послужил результатом физического эксперимента.
Если график функции симметричен относительно оси ординат, то y(x) — четная функция.
Если график функции симметричен относительно оси абсцисс, то x(y) — четная функция. x(y) — функция, обратная функции y(x).
Если график функции симметричен относительно начала координат (0,0), то y(x) — нечетная функция. Нечетной будет также обратная функция x(y). Важно помнить, что понятие о четности и нечетности функции имеет прямую связь с областью определения функции. Если, например, четная либо нечетная функция не существует при х=5, то она не существует и при х=-5, чего нельзя сказать про функцию общего вида. При установлении четности и нечетности обращайте внимание на область определения функции.

Исследование функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции достаточно рассмотреть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает значения от А до В, то те же значения она будет принимать и при x<0.
Для нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну часть функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).

www.kakprosto.ru

Как определить функцию по графику

Содержание Инструкция Координата абсолютно любой точки на плоскости определяется двумя ее величинами: по оси абсцисс и оси ординат. Совокупность множества таких точек и представляет собой график функции. По нему вы видите, как меняется значение Y в зависимости от изменения значения Х. Также вы можете определить, на каком участке (промежутке) функция возрастает, а на каком убывает. Инструкция Что можно сказать о функции, если ее график представляет собой прямую линию? Посмотрите, проходит ли эта прямая через точку начала отсчета координат (то есть, ту, где величины Х и Y равны 0). Если проходит, то такая функция описывается уравнением y = kx. Легко понять, что чем больше будет значение k, тем ближе к оси ординат будет располагаться эта прямая. А сама ось Y фактически соответствует бесконечно большому значению k. Посмотрите на направлении функции. Если она идет «слева снизу – направо наверх», то есть через 3-ю и 1-ю координатные четверти, она возрастающая, если же «слева сверху – направо вниз» (через 2-ю и 4-ю четверти), то она убывающая. Когда прямая не проходит через начало координат, она описывается уравнением y = kx + b. Прямая пересекает ось ординат в точке, где y = b, и значение y может быть как положительным, так и отрицательным. Функция называется параболой, если описывается уравнением y = x^n, и ее вид зависит от величины n. Если n – любое четное число (простейший случай – квадратичная функция y = x^2), график функции представляет собой кривую, проходящую через точку начала координат, а также через точки с координатами (1;1), (-1;1), поскольку единица в любой степени останется единицей. Все значения y, соответствующие любым значениям X, отличным от нуля, могут быть только положительными. Функция симметрична относительно оси Y, а ее график расположен в 1-й и 2-й координатных четвертях. Легко можно понять, что чем больше величина n, тем приближеннее график будет к оси Y. Если n – нечетное число, график этой функции представляет собой кубическую параболу. Кривая располагается в 1-й и 3-й координатных четвертях, симметрична относительно оси Y и проходит через начало координат, а также через точки (-1;-1), (1;1). Когда квадратичная функция представляет собой уравнение y = ax^2 + bx + c, форма параболы совпадает с формой в простейшем случае (y = x^2), однако ее вершина не находится в точке начала координат. Функция называется гиперболой, если она описывается уравнением y = k/x. Легко можно видеть, что при значении х, стремящемся к 0, значение y возрастает до бесконечности. График функции представляет собой кривую, состоящую из двух ветвей и располагающуюся в разных координатных четвертях.

completerepair.ru

Как определить периодичность функции 🚩 периодичность функций 🚩 Математика

26 сентября 2011

Автор КакПросто!

По школьным урокам математики каждый помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный промежуток — обладают и многие другие функции. Они называются периодическими. Периодичность — очень важное свойство функции, часто встречающееся в различных задачах. Поэтому полезно уметь определять, является ли функция периодической.

Статьи по теме:

Инструкция

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

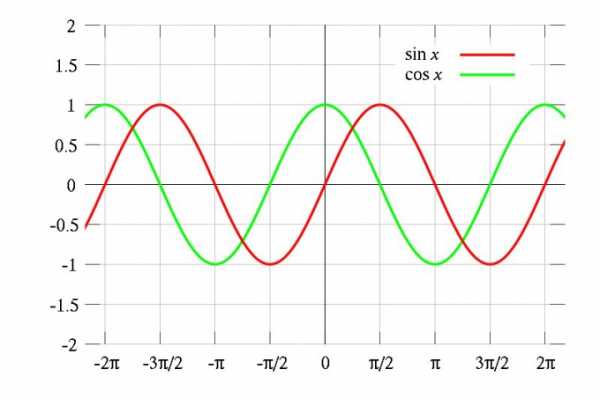
Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.

Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.

Периодической функцией называется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции называется число, при добавление которого к аргументу функции значение функции не меняется.

Вам понадобится

• Знания по элементарной математике и началам анализа.

Инструкция

Обозначим период функции f(x) через число К. Наша задача найти это значение К. Для этого предположим, что функция f(x), пользуясь определением периодической функции, приравняем f(x+K)=f(x). Решаем полученное уравнение относительно неизвестной K, так, как будто x — константа. В зависимости от значения К получится несколько вариантов. Если K>0 — то это и есть период вашей функции.

Если K=0 — то функция f(x) не является периодической.

Если решение уравнения f(x+K)=f(x) не существует ни при каком K не равном нулю, то такая функция называется апериодической и у неё тоже нет периода.

Видео по теме

Обратите внимание

Все тригонометрические функции являются периодическими, а все полиномиальные со степенью больше 2 — апериодическими.

Полезный совет

Периодом функции, состоящей из двух периодический функций, является Наименьшее общее кратное периодов этих функций.

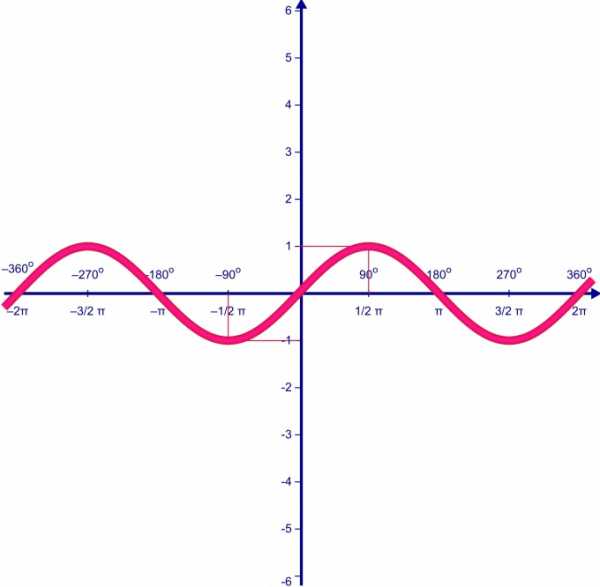
Если рассматривать точки на окружности, то точки x, x + 2π, x + 4π и т.д. совпадают друг с другом. Таким образом, тригонометрические функции на прямой периодически повторяют свое значение. Если известен период функции, можно построить функцию на этом периоде и повторить ее на других.

Инструкция

Период — это число T, такое что f(x) = f(x+T). Чтобы найти период, решают соответствующее уравнение, подставляя в качестве аргумента x и x+T. При этом пользуются уже известными периодами для функций. Для функций синуса и косинуса период составляет 2π, а для тангенса и котангенса — π.

Пусть дана функция f(x) = sin^2(10x). Рассмотрите выражение sin^2(10x) = sin^2(10(x+T)). Воспользуйтесь формулой для понижения степени: sin^2(x) = (1 — cos 2x)/2. Тогда получите 1 — cos 20x = 1 — cos 20(x+T) или cos 20x = cos (20x+20T). Зная, что период косинуса равен 2π, 20T = 2&#960. Значит, T = π/10. Т — наименьший положительный период, а функция будет повторяться и через 2Т, и через 3Т, и в другую сторону по оси: -T, -2T и т.д.

Полезный совет

Пользуйтесь формулами для понижения степени функции. Если вам уже известны периоды каких-либо функций, пробуйте свести имеющуюся функцию к известным.

Функция, значения которой повторяются через определенное число, называется периодической. То есть сколько бы периодов вы ни прибавили к значению х, функция будет равна одному и тому же числу. Любое исследование периодических функций начинается с поиска наименьшего периода, чтобы не выполнять лишнюю работу: достаточно изучить все свойства на отрезке, равном периоду.

Инструкция

Воспользуйтесь определением периодической функции. Все значения х в функции замените на (х+Т), где Т – наименьший период функции. Решите полученное уравнение, считая Т неизвестным числом.

В результате вы получите некое тождество, из него попробуйте подобрать минимальный период. Например, если получилось равенство sin(2T)=0,5, следовательно, 2Т=П/6, то есть Т=П/12.

Если равенство получается верным только при Т=0 или параметр Т зависит от х (например, получилось равенство 2Т=х), делайте вывод о том, что функция не периодична. Для того чтобы узнать наименьший период функции, содержащей лишь одно тригонометрическое выражение, воспользуйтесь правилом. Если в выражении стоит sin или cos, периодом для функции будет 2П, а для функций tg, ctg ставьте наименьший период П. Учтите при этом, что функция не должна быть возведена в какую-либо степень, а переменная под знаком функции не должна быть умножена на число, отличное от 1. Если cos или sin внутри функции возведены в четную степень, уменьшите период 2П в два раза. Графически вы можете увидеть это так: график функции, расположенный ниже оси ох, симметрично отразится вверх, поэтому функция будет повторяться в два раза чаще.

Чтобы найти наименьший период функции при том, что угол х умножен на какое либо число, действуете так: определите стандартный период этой функции (например, для cos это 2П). Затем разделите его на множитель перед переменной. Это и будет искомый наименьший период. Уменьшение периода хорошо видно на графике: он сжимается ровно во столько раз, на сколько умножен угол под знаком тригонометрической функции.

Обратите внимание, если перед х стоит дробное число меньше 1, период увеличивается, то есть график, напротив, растягивается.

Если в вашем выражении две периодические функции умножены друг на друга, найдите наименьший период для каждой по отдельности. Затем определите наименьший общий множитель для них. Например, для периодов П и 2/3П наименьший общий множитель будет 3П (он делится без остатка как на П, так и на 2/3П).

www.kakprosto.ru