Пропорция уравнение – Уравнение пропорции. Решить уравнение пропорцией.

Решение пропорций | Математика

Рассмотрим решение пропорций на конкретных примерах. 

Решить уравнения с пропорцией:

 1)  25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:

   

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

   

Ответ: 45.

   

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

   

   

   

Ответ: 13,5.

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

   

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

   

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100,  мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10: 

   

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

   

Еще раз сокращаем 4 и 2 на 2:

   

   

Ответ: 18.

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

   

Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:

   

Смешанные числа переводим в неправильные дроби:

   

   

   

Ответ: 28.

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

   

Произведение крайних членов пропорции равно произведению средних членов:

   

Здесь удобно упростить уравнение, разделив обе части на 5:

   

   

   

   

   

   

Ответ: 10,5.

   

Произведение крайних членов пропорции равно произведению ее средних членов:

   

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

   

   

   

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Ответ: 1,12.

www.for6cl.uznateshe.ru

Уравнение пропорции и его решение

Определение и уравнение пропорции

ОПРЕДЕЛЕНИЕ Пропорцией называется равенство двух отношений: или .

Например. или

ОПРЕДЕЛЕНИЕ Величины и называются крайними членами, а величины и — средними членами пропорции.

Если равенство верно, то пропорция называется правильной.

Например. Пропорция , является правильной, поскольку и

Основное свойство пропорции

Основное свойство пропорции. В правильной пропорции произведение крайних равно произведению средних ее членов:

   

Чтобы найти неизвестный крайний член пропорции, надо перемножить средние члены и произведение разделить на известный крайний член:

   

Чтобы найти неизвестный средний член пропорции, надо перемножить крайние члены~ и произведение разделить на известный средний член.

   

ПРИМЕР 1

Задание	Решить уравнение
Решение	Если данное уравнение рассматривать как пропорцию, то неизвестным является ее средний член, а тогда
Ответ

ru.solverbook.com

Как решать уравнения с пропорциями онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Довольно часто в математике встречаются простые линейные уравнения, которые сильно напоминают обыкновенную пропорцию. Например, вот такое уравнение:

\[\frac{x}{2} = \frac{4}{5}\]

Чтобы решить уравнениt с пропорцией применяют правила креста. Данное правило заключается в том, что если в члене пропорции имеются знаки «\[+\] или \[-\], то в обязательном порядке необходимо взять данный член пропорции в скобки перед применением правила пропорции.

Так же читайте нашу статью «Решить уравнение с разделяющими переменными онлайн»

Другими словами данное правило можно описать так: если нарисовать крест поверх пропорции, то произведения членов пропорции, лежащих на концах креста, равны.

Допустим, дано уравнения следующего вида, которое мы решим используя правила пропорции:

\[x \cdot 5 = 2 \cdot 4\]

Оперируя простыми арифметически действиями, решим данное уравнение:

\[5x = 8 \mid \div 5\]

\[\frac{5x}{5} = \frac{8}{5}\]

\[x = \frac{8}{5}\]

\[x = 1\frac{3}{5}\]

Все предельно просто, главное помнить правила пропорции и не забывать о смене знака на противоположные при переносе члена с одной стороны на другую.

Где можно решить уравнение пропорцией онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Задачи и задания на пропорции: примеры и решение

Решение заданий на пропорции

Если один из членов пропорции неизвестен и надо его найти, то говорят, что надо решить пропорцию. Решение пропорций всегда выполняется с помощью свойства пропорции.

Задание 1. Найдите неизвестный член пропорции:

a)	x	=	3	;     б)	1	=	5
	2		1		3		x

Решение: Так как неизвестны крайние члены пропорции, то для их нахождения надо умножить средние члены и разделить полученный результат на известный крайний член:

a) x =	2 · 3	,   x = 6.	б) x =	3 · 5	,   x = 15.
	1			1

Ответ: а) x = 6, б) x = 15.

Задание 2. Решите пропорции:

a)	30	=	5	;     б)	7	=	x
	x		8		5		10

Решение: Так как неизвестны средние члены пропорции, то для их нахождения надо умножить крайние члены и разделить полученный результат на известный средний член:

a) x =	30 · 8	,   x = 48.	б) x =	7 · 10	,   x = 14.
	5			5

Ответ: а) x = 48, б) x = 14.

Задание 3. Известно, что 21x = 14y. Найдите отношение x к y.

Решение: сначала сократим обе части равенства на общий множитель 7:

получим:

3x = 2y

Теперь разделим обе части на 3y, чтобы в левой части у

x убрать множитель 3, а в правой части избавиться от y:

После сокращения отношений у нас остаётся:

Ответ: 2 к 3.

Задачи на пропорции с решением

Задача 1. Из 300 читателей библиотеки 108 человек – студенты. Какой процент всех читателей составляют студенты?

Решение: Примем всех читателей библиотеки за 100% и запишем условие задачи кратко:

300 – 100%
108 – ?%

Составим пропорцию:

Найдём x:

x =	108 · 100	= 36
	300

Ответ: 36% всех читателей составляют студенты.

Задача 2. При варке варенья используют ягоды и сахар в отношении 5:2. Сколько надо ягод, если взяли 450 грамм сахара?

Решение: составим пропорцию:

Найдём x:

x =	5 · 450	= 1125
	2

Ответ: На 450 гр сахара надо взять 1125 гр ягод.

naobumium.info

Урок «Пропорции и уравнения 6 класс»

Министерство образования Республики Саха (Якутия)

Ленское районное управление образования

Муниципальное бюджетное образовательное учреждение

«Средняя общеобразовательная школа п. Пеледуй» муниципального

образования «Ленский район» Республики Саха (Якутия)

Урок «Пропорции и уравнения 6 класс»

Учитель математики

Николаева А.П.

Пеледуй, 2017 год

Открытый урок по математике 6 класс

Тема: «Пропорции и уравнения»

Цель урока:1) обучение решению задач разными способами

2) научить мыслить и управлять своей мыслью для решения задач

3) научить понимать силу и красоту математики

Тип урока: игра, урок проводится во время декады математики в школе

Оборудование: плакаты, карточки, видеопроектор

«Человек разумный» есть в первую очередь «человек играющий» , поэтому обучать даже самым серьезным вещам следует по возможности играя, эта мысль приходила в голову выдающимся педагогам на протяжении всей истории человечества.

Девиз: «Для того, чтобы научиться решать задачи, нужно решать их»

Мудрые мысли: 1) « Предмет математики настолько серьезен, что полезно не упускать случаев, делать его немного занимательным» Б.Паскаль

2) «Больше думай, не болтай, но и формул, правил ты не забывай»

Открытие

В труде применяем сложение,

Сложению и честь и почет;

К умению прибавим терпение,

А сумма –успех принесет!

Нельзя забывать вычитание

Чтоб зря не потратился день,

Из суммы старанья и знания

Мы вычтем безделье и лень!

В труде умножение поможет

Чтоб дельной работа была,

Сократ трудолюбие умножит-

Умножаться наши дела

Деление нам служит на деле,

Оно нам поможет всегда:

Кто поровну трудности делит,

Разделит успехи труда!

Поможет любое из действий,

Они нам удачу несут

И в жизни поэтому вместе

Шагают наука и труд!

Представление команд :

«Математики» Девиз: «К математике способность проявляй, лениться мысли не позволяй»

« Пифагорейцы»: Девиз: «Посредством уравнений ,теорем мы уйму разрешим проблем»

1 конкурс Из истории математики ( это задание было дано заранее )

А) Пропорции

Слово «пропорция» означает «соразмерность», Определенное соотношение частей между собой»

Учение об отношениях и пропорциях особенно успешно развивалось в 4 веке до н.э. в Древней Греции, славившейся произведением искусства, архитектуры, развитыми ремеслами. С Пропорциями связано представление о красоте, порядке и гармонии о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в « Началах» Евклида ( 3 век до н.э.) там приводится и доказательство основного свойства пропорции. Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного изображения предмета. Знаменитая скульптура Аполлона Бельведерского разделена в таком отношении, которое называют « Золотое Сечение». Окружающие нас предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длины, близкое к числу 0,618. Рассматривая расположение листьев на общем стебле растений, можно заметить, что отношение расстояния между парами листьев является примером «Золотого сечения»

Красивейшее произведение древнегреческой архитектуры, Парфенон, было построено в 5 веке до н.э. Отношение высоты фасада здания к его длине равно о,618

Б) Уравнения

Среди задач, которые с древних времен приходилось решать людям. Много было похожих, однотипных: вычисление площадей участков, нахождение объемов фигур определенной формы, деление доходов, вычисление стоимости товара, измерение массы с помощью различных единиц и другие.

Для однотипных задач в разное время, в разных странах пытались отыскать общие способы, правила решения. В этих правилах рассказывалось, как найти неизвестную величину через данные числа для группы похожих задач. Так возникла алгебра,_ один из разделов математики, в котором вначале в основном рассматривалось решение различных уравнений.

Некоторые алгебраические понятия и общее примеры решения задач знали уже в Древнем Вавилоне и Египте более 4000лет назад. Большой вклад в создание алгебры внес выдающийся древнегреческий математик ДИОФАНТ (3 век), которого по праву считают «отцом алгебры». Диофант умел решать очень сложные уравнения, применял для неизвестных буквенные обозначения, ввел специальный символ вычитания, использовал сокращение слов

В начале нашей эры греческая наука и культура пришли в упадок. Но к этому времени больших успехов в развитии математики достигли индийские ученые. С 5 по 12век ими было сделано много открытий. Культуру древних индейцев усвоили их соседи: арабы, узбеки, персы, таджики другие народы. И в 9-15 веке мировым центром наук становится Средняя Азия, подарившая миру много ученых математиков. Их труды оказали большое влияние на развитие науки в Европе.

Конкурс капитанов

1. Что за чиж на черном поле 1) Говорит она без звучно,

Чертит клювом белый след? Но понятно и не скучно,

У чижа ни ног, ни крыльев, Ты беседуй чаще с ней

Ни пера, ни пуха нет (мел) станешь лучше и умней ( книга)

2. Ног нет, а хожу Что проходит сквозь окно, не боится

Рта нет, а скажу: никого (луч света)

Когда спать, когда вставать (будильник)

3)Не видно и не слышно ее Она всегда с трудом дается нам

Стоит заговорить о ней Зато потом, когда ответ получен,

И она исчезнет (тишина) То словно свет блеснет по сторонам,

Где только, что еще бродили тучи ) (задача)

Разминка команд

1. У семи братьев по одной сестрице, много сестер? ( одна)

2. Ты да я , да мы с тобой. Много ли нас стало? (двое)

3. Я –цифра, меньше десяти, меня тебе легко найти

Но если букве Я прикажешь рядом встать,

Я все: отец, и ты, и дедушка, и мать ( семь семья)

4)Я приношу с собою боль

Лица на форме искажения, а Ф на П заменишь коль

То я всего лишь знак сложения ( флюс плюс)

Вопросы болельщикам

Арифметический я знак, В задачниках меня найдешь во многих строчках, Лишь О ты вставишь, зная как

И я _ географическая точка( плюс полюс)

Я не люблю у школьников быть в дневнике,

Ему из-за меня вся не мила природа

Но если внутрь меня поставишь Е

То- среди женского я рода (два дева)

Задание командам

Определите, является ли прямо пропорциональной, обратно пропорциональной зависимость между величинами:

1 путем, пройденным машиной с постоянной скоростью и временем ее

Движения

2 стоимостью товара, купленного по одной цене, и его количеством

3 площадью квадрата и длиной его стороны

4 массой стального бруска и его объемом

5 числом рабочих, выполняющих с одинаковой производительностью труда

Некоторую работу, и временем выполнения этой работы.

6 Стоимостью товара и его количеством, купленным на определенную сумму денег

7 Объемом куба и длиной его ребра

8 Периметром квадрата и длиной его стороны.

ЗАДАНИЕ КОМАНДАМ

Каждой команде и болельщикам раздаются карточки с заданием: реши уравнение, реши две задачи. Верно выполненное задание приносит команде 3 балла, эти баллы умножаются на количество участников команды. Баллы болельщиков прибавляются к баллам участников команды.

ЗАМОРОЧКИ ИЗ БОЧКИ

1 Что называется пропорцией?

2 Приведи пример пропорции в буквенном виде, как называется каждая буква для пропорции

3 Назови основное свойство пропорции

4 Что называется уравнением?

5 Что такое корень уравнения?

6 Продолжи фразу:

А) Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части уравнения в другую,( изменив при этом его знак)

Б) корни уравнения не изменятся, если обе части уравнения умножить или разделить ( на одно и то же число, не равное нулю)

7 Какое двузначное число при отражении в зеркале увеличится в 4,5 раза

(18 и 81 )

8 На листе написано число 66. Как увеличить это число в полтора раза, не делая над ним никаких действий. ( 66 перевернуть лист 99)

9 Сколько раз нужно распилить 5-ти метровое бревно, чтобы получить метровые чурки (4 раза )

10) 60 листов книги имеют толщину 1см. Какова толщина всех листов книги, если в ней 240 страниц (2 см)

ЗАДАНИЕ КОМАНДАМ И БОЛЕЛЬЩИКАМ ( использован местный материал)

Работник «Сургутнефтегаз» от поселка Пеледуй до поселка Витим, расстояние

между которыми 30 км, ехал на легковой машине со скоростью 6о км\ч, а от

Витима до Талака на ехал на автобусе для рабочих вахты, скорость которого в

1,5 раза меньше легковой машины. На весь путь работник затратил 3,5 часа. Найти расстояние от Витима до Талакана

infourok.ru

Урок математики «Пропорция. Решение уравнений»

МБОУ «Большеатнинская СОШ»

Атнинского муниципального района Республики Татарстан

Разработка урока математики

по теме «Пропорция. Решение

уравнений» (6 класс)

2014 год

План конспект урока математики в 6 классе

Тема: «Пропорция. Решение уравнений.»

Цель: формировать навык нахождения неизвестных членов пропорции, решения уравнений, имеющих вид пропорции;

закрепить основное свойство пропорции на практике: при решении задач и при решении уравнений;

воспитывать умение оценивать объективно труд своих товарищей.

Тип урока: урок повторения изученного материала..

Вид урока: комбинированный.

Оборудование: учебник, интерактивная доска.

Ход урока:

1.Организационный момент.

Посмотрите, всё ль в порядке:

Книжка, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

2. Устный счет.

Тейк офф – тач даун (встает тот, кто знает ответ на заданный вопрос)

1. У стола квадратной формы отпилили 1 угол. Сколько углов осталось? (5)

2. Сколько концов у трех с половиной палок? (8)

3. Врач прописал 5 уколов. Через полчаса — по уколу. Через сколько часов после первого укола будет сделан последний укол? (2ч.)

4. На столе горят 7 свечей, 3 свечи потушили. Сколько свечей останется на столе через 5-6 часов? (3)

5. Назовите взаимно обратные числа.(3/5 и 5/3; 2,5 и 2,5)

6. Найдите 10% от 500; 40% от 300; 50% от 600; 100% от 520.

3. Актуализация знаний.

1) Найдите отношения:

А) 12кг к 400г; (30)

Б) 40м к 2 км; (0,02)

Какой вывод можно сделать? (Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения).

2) Как называется равенство двух отношений? (пропорция)

4. Сообщение темы урока.

Континиус Раунд Робин (учитель задает вопрос и дает время подумать; четыре ученика в команде по очереди отвечают по кругу до того момента, пока учитель не остановит процесс).

Подумайте, что вы знаете про пропорции? (анализ ответов учащихся)

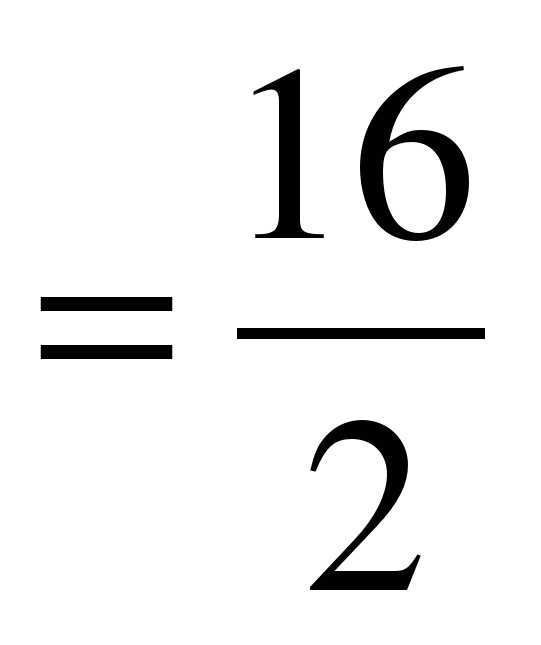
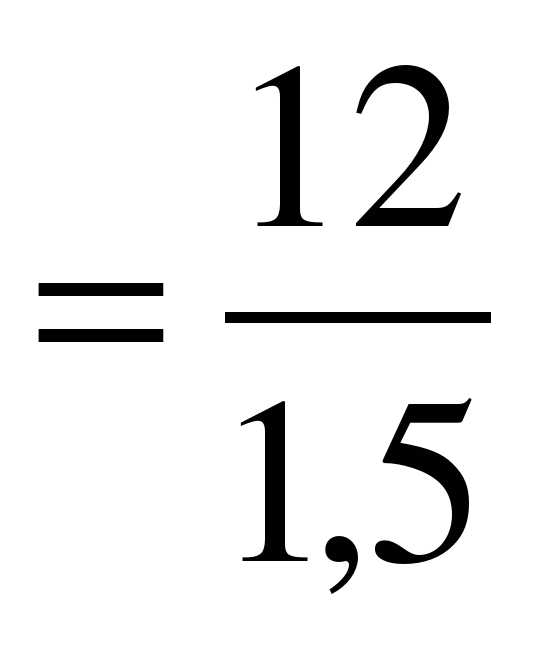
С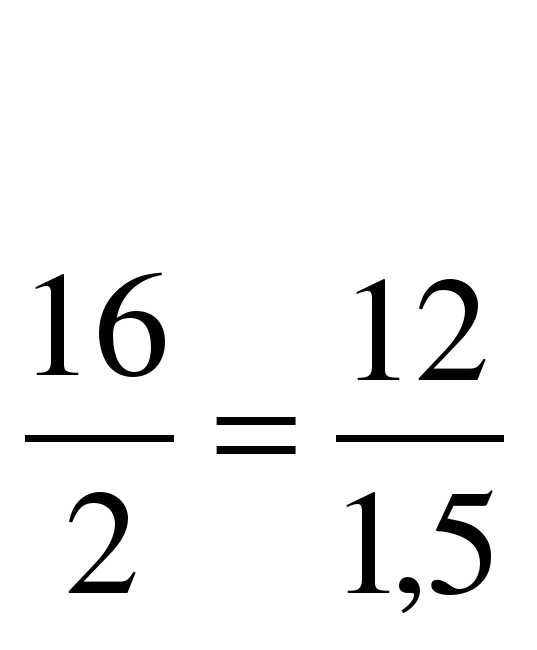егодня на уроке продолжим работу над темой «Пропорция». Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где?

16 : 2 =8; 12 : 1,5 = 8;

Что вы можете сказать про эти записи? (Равенство двух отношении называется пропорцией).

Как называются 16 и 1,5? (крайние члены пропорции).

Как называются 2 и 12? (средние члены пропорции).

Как определить пропорция верна или неверна? (основное свойство пропорции).

Как найти неизвестный крайний член пропорции?

Как найти неизвестный средний член пропорции?

Что произойдет, если поменять местами крайние или средние члены пропорции? (получившиеся новые пропорции тоже верны).

5. Закрепление. Работа в тетрадях.

Задача: Настоящие охотники за приведениями получили новое оборудование – ультрасовременные ловушки. Две такие ловушки захватывают за один раз 18 приведений. Сколько ловушек надо взять на операцию, чтобы отловить одновременно 27 приведений?

2л – 18приведении

Хл — 27приведении

Составляем пропорцию и решаем её. Ответ: 3 ловушки.

Задача 2. Решение уравнений.

№777 (решить уравнения) используя структуру Финк — Райт – Раунд Робин (учитель задает вопрос и дает время подумать; ученики думают и записывают ответы на свой листочек; ученики по очереди зачитывают свой ответ с листочка).

Пришло время ответить на вопрос, заданный в начале урока. Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где? Для ответов мы используем структуру Таймд Пэа Шэа (учитель задает вопрос и дает время подумать; учитель озвучивает, кто начинает первым и сколько времени дается каждому из учеников для ответа; два ученика отвечают на вопрос по очереди в течение данного времени).

6.Домашнее задание №798(составить пропорцию), №799 (при каком значении х верна пропорция) на стр.131.

7. Самостоятельная работа. Выполнение теста по теме «Пропорция» (ваши тесты будут служит билетиками на выход).

8. Подведение итогов урока.

Как связаны между собой понятия «отношение» и «пропорция»?

Что называют отношение двух чисел?

Как называется равенство двух отношений?

Что называется пропорцией?

Каким свойством обладает пропорция?

videouroki.net

Конспект урока по теме «Решение уравнений с помощью пропорции»

Математика, 6 класс Дата____________ Учитель: Чакал Э.М.

Тема: «Решение уравнений с помощью пропорции».

Цели урока:

1. Обучающие: закрепить понятия: пропорция, ее крайние и средние члены; основное свойство пропорции; закрепить эти понятия на решении уравнений и задач.

2. Развивающие: развитие кругозора, мышления, внимания, культуры математической речи, привитие интереса к изучению математики.

3. Воспитательные: воспитание аккуратности, чувство коллективизма, самоконтроля.

Ход урока.

1. Организационный момент.

2. Мотивация урока.

В древности, наблюдая за окружающей природой и создавая произведения искусства, люди искали закономерности, которые позволяли бы определить прекрасное, т.е. пытались вывести формулу красоты. Ряд “формул красоты” известен. Это правильные геометрические формы: квадрат, круг, равносторонний треугольник и т. д. Эстетическое наслаждение, получаемое человеком при наблюдении совершенных форм, объясняется “божественным отношением” или “золотым сечением”. Соблюдение определенных отношений в природе, искусстве, архитектуре означает соблюдение определенных отношений между размерами отдельных частей растений, скульптуры, здания “Золотое сечение” являлось критерием гармонии и красоты во времена Пифагора и в эпоху возрождения. И об этом мы поговорим сегодня на уроке.

3. Актуализация опорных знаний. Проверка д/з.

Что называется отношением двух чисел?

Что показывает отношение двух чисел?

Что такое пропорция?

Сформулируйте основное свойство пропорции?

Устные задания :

Найти отношение:

а) ; б) .

Верна ли пропорция:

а) ; б)

За 6 ч поезд прошел 480 км. Какой путь прошел поезд за первые 2 ч, если его скорость была постоянна?

Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку. Сколько килограмм сахарного песку надо взять на 12 кг ягод?

4. Решение уравнений на основное свойство пропорции.

Решить № 56-58(а,б)

5. Историческая пауза.

На знаменитой картине Леонардо Да Винчи «Мадонна в скалах» с очевидностью просматриваются линии “золотого сечения”. Голова Мадонны делит длину картины по золотому сечению. При желании можно с успехом продолжить деление картины по “золотому сечению” и дальше. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении “золотого сечения”, придают ей характер уравновешенности и спокойствия. Скульптурные творения греческих мастеров Фидия, Политекта, Мирона, Праксителя по праву считаются эталонами красоты человеческого тела. Оценивая фигуру того или иного человека, мы невольно сравниваем ее с этими признанными эталонами (рис. № 5) По мнению многих искусствоведов, художников, скульпторов эпохи Возрождения, основные пропорции человеческого тела подчинены законам “золотого сечения”.Немецкий профессор–искусствовед А. Цейзинг (XIX век) утверждал, что фигура идеально сложенного человека должна подчиняться следующим закономерностям. Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

Как вы думаете, тело мужчины или женщины ближе всего к идеалу?

Мужчины! Чтобы приблизиться к идеалу, женщины надевают туфли на каблуках. Оказывается, что у женщин ноги короче, чем у мужчин.

Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к пропорциям золотого сечения, чем пропорции женского тела, в отношении которого среднее значение выражается в соотношении 8: 5 = 1,6. Давайте теперь вместе ответим на вопрос: “Зачем учить математике, где она пригодится в жизни?”

6. Тестовая работа.

I вариант

1. Решить уравнение: 6,4:0,16=4:х

1) 10; 2) 2,5; 3) 0,1; 4) 1.

2. Решить задачу:

Для 10 порций салата требуется 200г лука. На сколько порций хватит 60г лука?

1) 3; 2) 4; 3) 2; 4) 9.

II вариант

1. Решить уравнение: 0,75:1,5=5:х

1) 10; 2) 2,5; 3) 0,1; 4) 1

2. Решить задачу:

6 рабочих могут выполнить работу за 12 дней. Сколько ещё надо нанять рабочих, чтобы выполнить эту работу за 8 дней?

1) 3; 2) 4; 3) 2; 4) 9.

7. Итоги урока. Рефлексия. Д/з.

Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).

Вам для этого помогут слова:

-Я узнал…

-Я почувствовал…

-Я увидел…

-Я сначала испугался, а потом…

-Я заметил, что …

-Я сейчас слушаю и думаю…

-Мне интересно следить за…

Решить № 56-58 (в,г)

infourok.ru