найти производную по направлению вектора в точке — 13 Сентября 2015 — Примеры решений задач
а) Дана функция z=z(x,y) , направляющий вектор l и точка А. Найти производную по направлению в точке.
Решение.Формула производной по направлению:
1) Находим частные производные:
2) Находим значение частных производных в точке A(-2; 0):
Частные производные можно найти с помощью калькулятора частные производные.
3) Находим направляющие косинусы:
Направляющие косинусы, т.е. координаты нормированного (единичного) вектора можно найти с помощью калькулятора нормировки вектора.
4) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:
Следующий пример.
б) Дана функция z=z(x,y) , точка А и точка N.
Найти производную в точке A по направлению точки N.
Решение. Выполнение первых двух пунктов решения совпадает с примером 1, поэтому начинаем с пункта 3.
3) Находим координаты направляющего вектора l:
4) Находим направляющие косинусы:
5) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:
Второй способ найти производную функции по направлению см. градиент функции.
www.reshim.su
4.1.4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «Производная по направлению. Градиент»
Задача 1.
Составить уравнение касательной плоскости к поверхности
Указание
Уравнение касательной плоскости к поверхности
В точке (Х0, Y0, Z0) имеет вид:
Решение
Подставим эти значения в уравнение касательной плоскости:Ответ:
Задача 2.
Составить уравнение касательной плоскости к поверхности
В точке (1,2,-1).
Указание
Найдите частные производные Z по Х и У как производные неявной функции:
Решение
Уравнение касательной плоскости:
Ответ:
Задача 3.
Составить уравнения нормали к поверхности
В точке (0,4,2).
Указание
Будем называть нормалью прямую, проходящую через данную точку перпендикулярно касательной плоскости, проведенной через эту точку. Тогда канонические уравнения нормали выглядят так:
Решение
Следовательно, канонические уравнения нормали:
Ответ:
Задача 4.
Найти производную функции
И точке М(2,-4) по направлению вектора MN, если N(-1,-8).
Указание
Производная функции Z = F (X, Y) в точке (Х0, У0) по направлению L, заданному вектором А = (Ха, Уа, Za), имеет вид:
Направляющие косинусы направления L.
Решение
Ответ: 9,2.
Задача 5.
Найти производную функции
В точке (3,2,1) по направлению, образующему с координатными осями равные тупые углы.
Указание
Причем
Решение
Найдем направляющие косинусы направления L, используя свойство направляющих косинусов:
(поскольку косинус тупого угла отрицателен).
Тогда
Ответ:
Задача 6.
Найти градиент функции
В точке А(6,10,-5).
Указание
Воспользуйтесь формулой
Решение
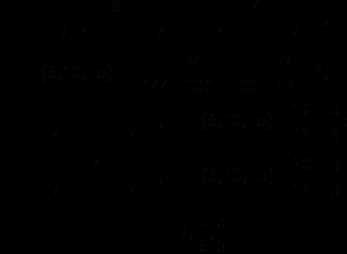
Ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Градиент
Градиент
Производная по направлению. Градиент
Пусть в некоторой области задана функция и точка . Проведем из точки вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку , т.е. .
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется производной от функции
в точке по
направлению вектора и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: ,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции и обозначается
или
(читается «набла у»): .
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
Свойства градиента
1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно .
2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.
Примеры решения задач
Пример 1. Найти производную от функции в точке по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
.
Следовательно, для направляющих косинусов вектора получим следующие значения:
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
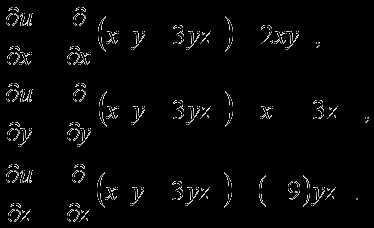
Вычислим значения этих частных производных первого порядка в точке :
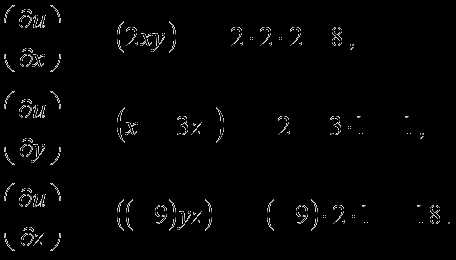
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна .
Пример 2. Найти градиент функции в точке .
Решение.
Поскольку градиентом функции называется вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, то для решения задачи сначала найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке :
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен .
Пример 3. Найти производную функции в точке по направлению градиента функции в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
В данном случае вектор совпадает
с градиентом функции
в точке :
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
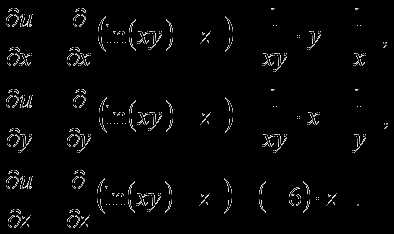
Вычислим значения частных производных первого порядка от функции
в точке :
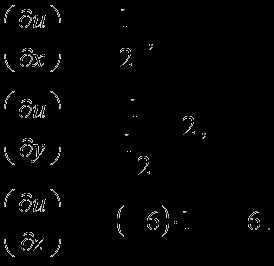
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: .
Найдем направляющие косинусы вектор по формулам:
.
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Задания для самостоятельной работы
1. Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке .
Ответ: .
5. Найти градиент функции
в точке .
Ответ: .
6. Найти градиент функции
в точке .
Ответ: .
1.4 Скалярное поле. Производная по направлению. Градиент
Предположим,
что в каждой точке М некоторой области D задано
значение скалярной
величины  ,
т. е. такой
величины, которая полностью характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом
,
т. е. такой
величины, которая полностью характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом  называют скалярной функцией точки и
записывают.
называют скалярной функцией точки и
записывают.
ОПРЕДЕЛЕНИЕ. Если
в области D задана скалярная функция точки 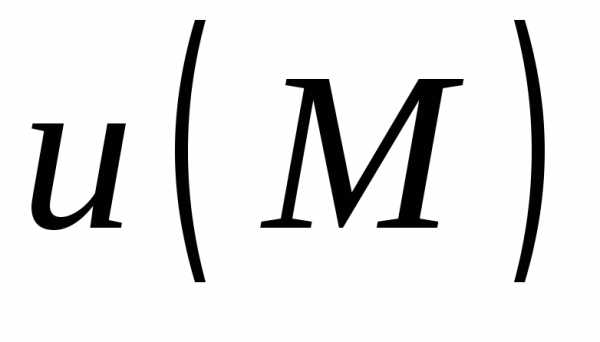 ,
то говорят, что в этой области задано
скалярное поле.
,
то говорят, что в этой области задано
скалярное поле.
Если
скалярное поле отнесено к системе
координат 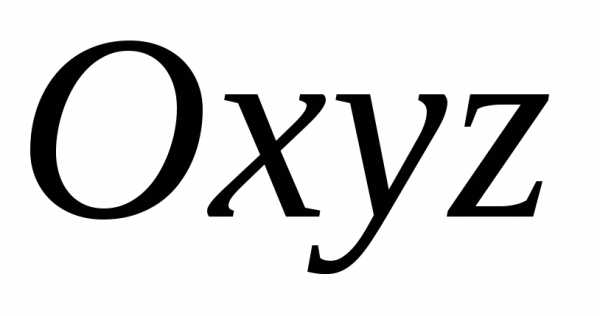 ,
то задание точкиМ равносильно
заданию ее координат
,
то задание точкиМ равносильно
заданию ее координат 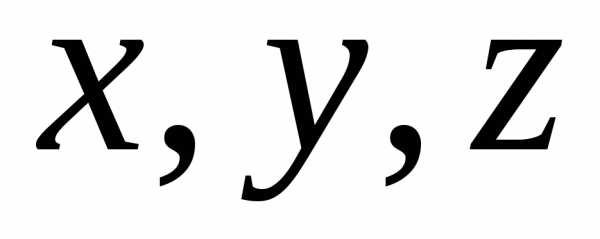 .
.
Поверхностью
уровня скалярного поля называют геометрическое
место точек, в которых функция  принимает постоянное значение, т. е.,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.
принимает постоянное значение, т. е.,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.
Пусть
задано скалярное поле, т. е. задана
функция
.
Возьмем точкуи некоторое направление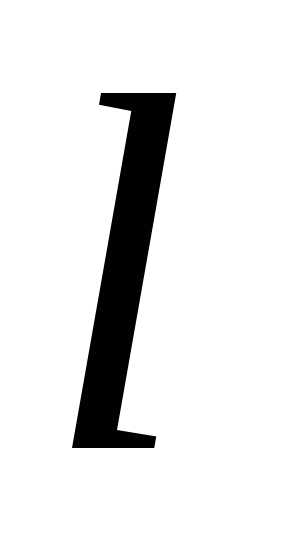 ,
определяемое направляющими косинусами.
При перемещении в данном направлении
точкив точкуфункцияполучает приращение
,
определяемое направляющими косинусами.
При перемещении в данном направлении
точкив точкуфункцияполучает приращение
,
которое
называют приращением функции в данном
направлении. Величину перемещения точки
обозначим через ,
тогда можно записать, что
,
тогда можно записать, что
.
ОПРЕДЕЛЕНИЕ. Производной
функции
в направлении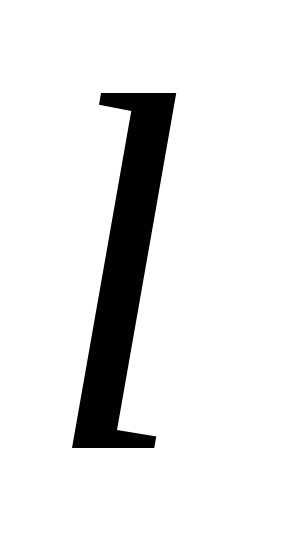 называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю
называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю
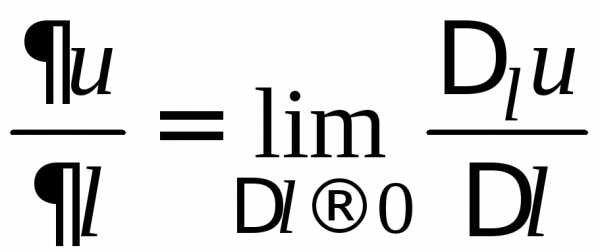 .
.
Вычислить производную по направлению можно, используя следующую теорему:
ТЕОРЕМА. Если
функция
дифференцируема, то ее производная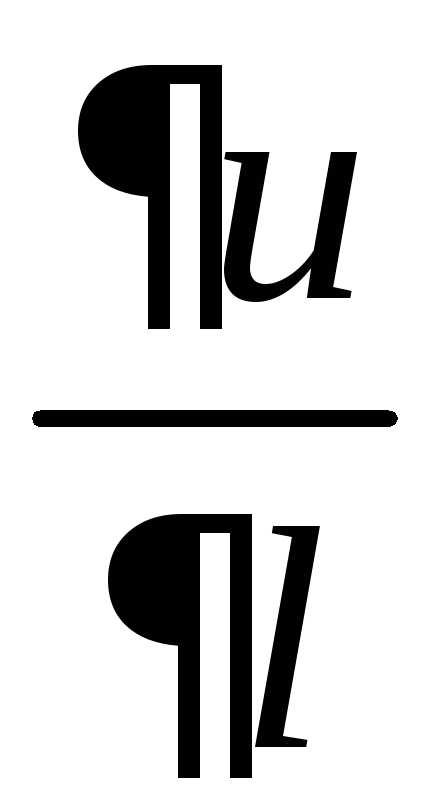 по любому направлению
по любому направлению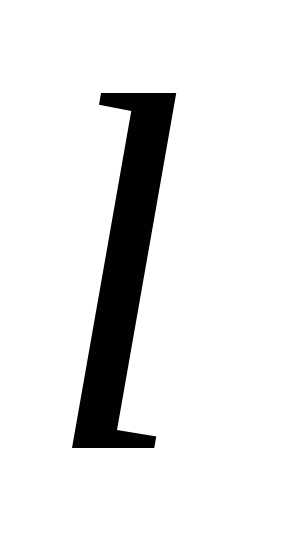 существует и равна
существует и равна
,
где
—
направляющие косинусы направления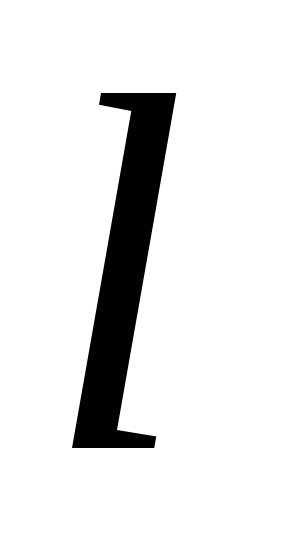 .
.
ПРИМЕР. Найти
производную функции
в точкепо направлению, идущему от точки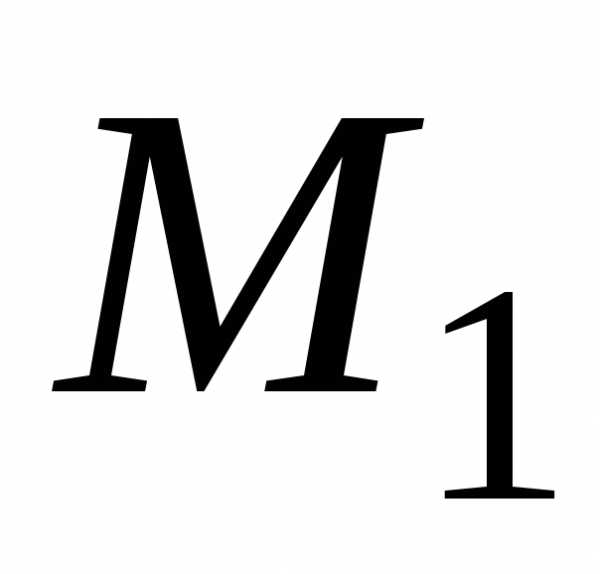 к точке.
к точке.
РЕШЕНИЕ
Найдем
единичный вектор e,
соответствующий направлению 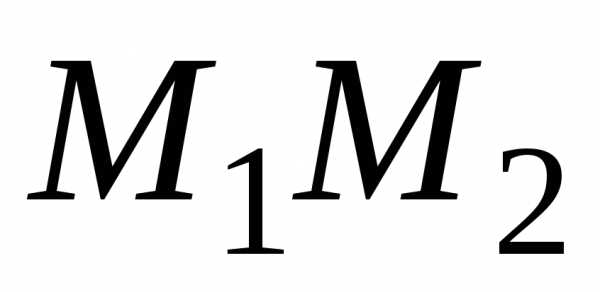 :
:
,
,
.
Частные
производные функции 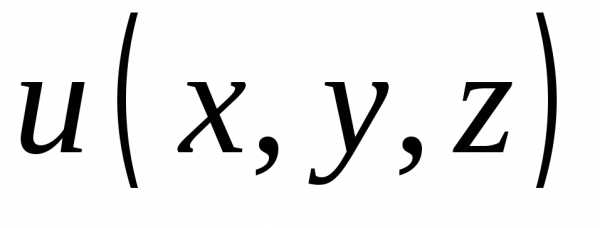 равны:
равны:
.
Вычислим
частные производные в точке 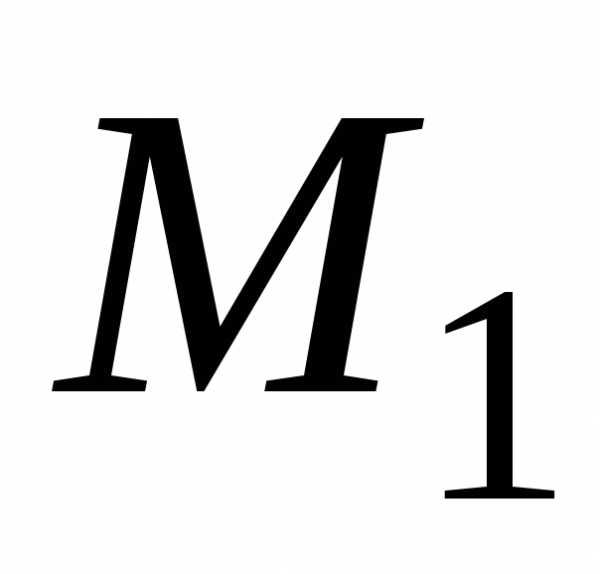 и найдем производную по направлению из
равенства
и найдем производную по направлению из
равенства
,
получим .
ОПРЕДЕЛЕНИЕ. Градиентом функции называют вектор, проекциями которого служат значения частных производных этой функции, т. е.
.
Используя определение градиента, формулу производной по направлению можно записать в виде:
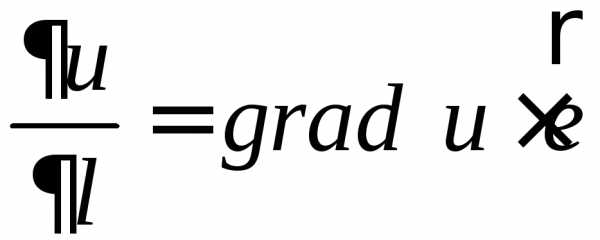 ,
,
где
— единичный вектор направления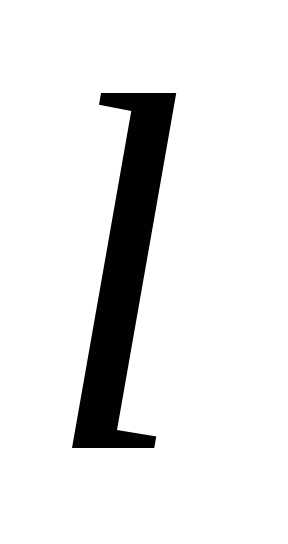 .
.
Меняя
направление 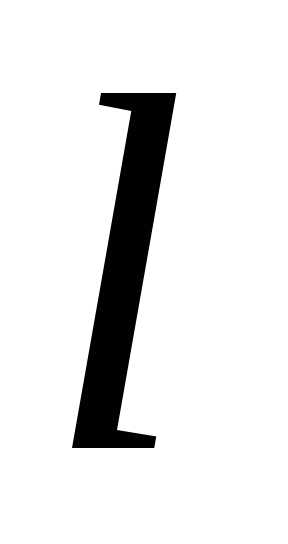 ,
мы будем получать различные значения
производной
,
мы будем получать различные значения
производной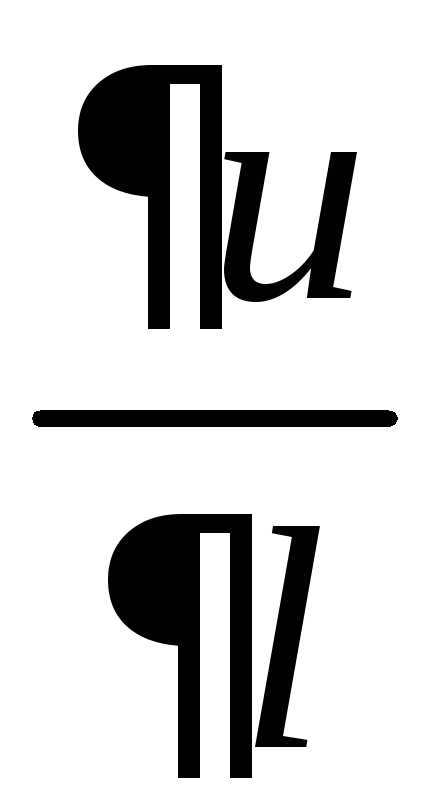 ,
причем наибольшее значение наблюдается,
когда направление
,
причем наибольшее значение наблюдается,
когда направление совпадает с вектором
совпадает с вектором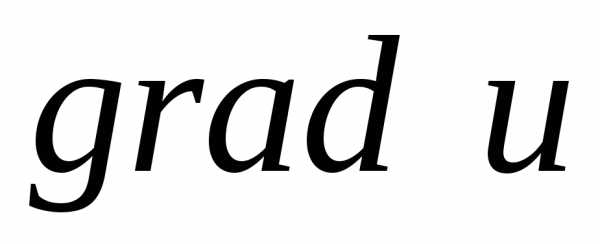 .
Таким образом,
.
Таким образом,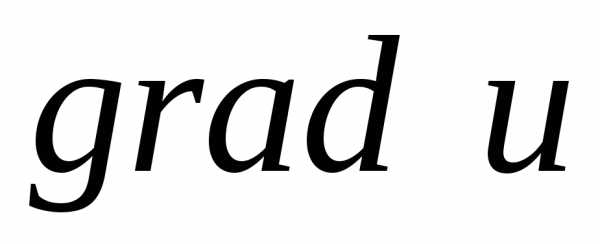 определяет направление, в котором
скорость возрастания функции является
наибольшей.
определяет направление, в котором
скорость возрастания функции является
наибольшей.
Градиент скалярного поля в данной точке по величине и направлению равен максимальной скорости изменения поля в данной точке.
ПРИМЕР. Дано
скалярное поле
.
Составить уравнение линии уровня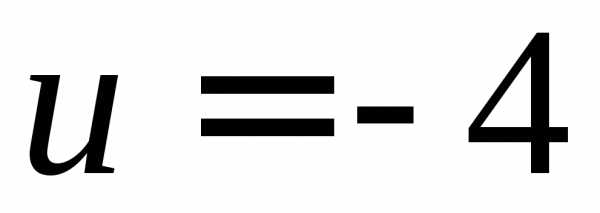 .
Вычислить с помощью градиента производную
скалярного поля в точке
.
Вычислить с помощью градиента производную
скалярного поля в точке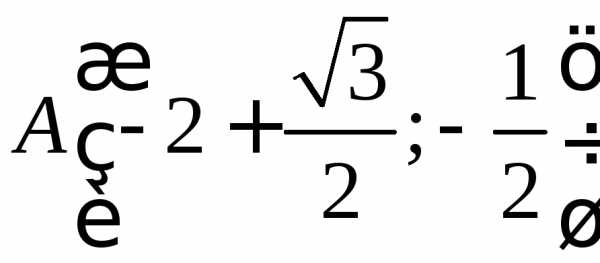 по направлению вектора
по направлению вектора .
Найти наибольшую скорость изменения
скалярного поля в точке
.
Найти наибольшую скорость изменения
скалярного поля в точке .
.
РЕШЕНИЕ
Поверхностью
уровня (линией уровня) данного скалярного
поля является окружность с центром в
точке 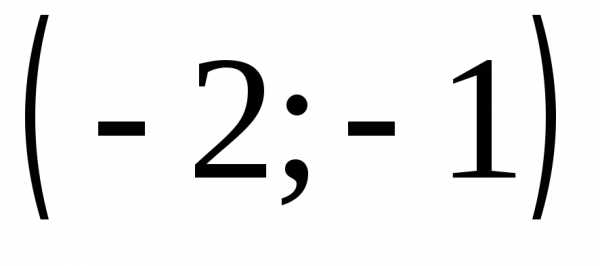 ,
радиуса 1:
,
радиуса 1:
, .
Градиент функции равен: .
Найдём
единичный вектор направления  :
: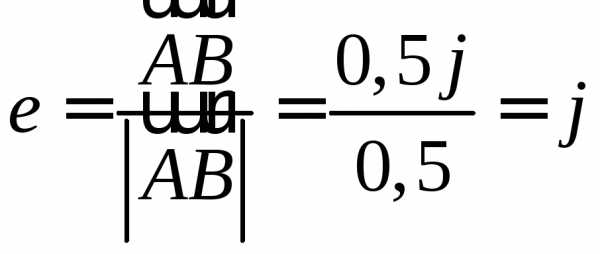 ,
а затем производную скалярного поля
,
а затем производную скалярного поля по направлению
по направлению в точке
в точке :
:
, 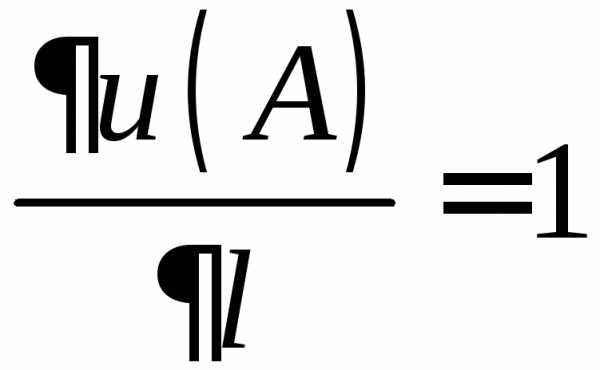 .
.
Так
как 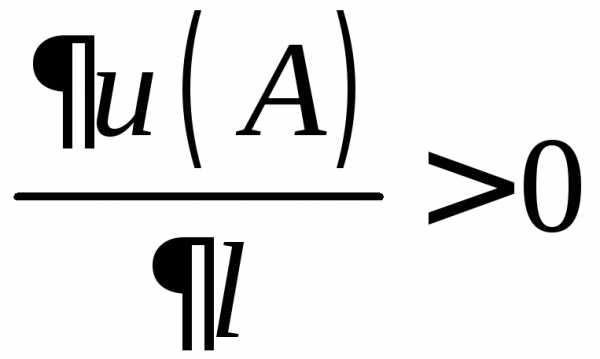 ,
то данное скалярное поле возрастает по
направлению вектора
,
то данное скалярное поле возрастает по
направлению вектора со скоростью равной 1.
со скоростью равной 1.
Теперь
найдём производную по направлению  :
:
, 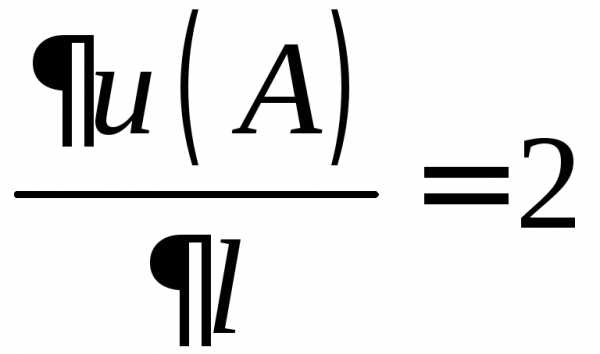 .
.
Наибольшая
скорость возрастания скалярного поля
в точке  равна 2.
равна 2.
studfiles.net
Пусть отрезок длины направлен по вектору
, ,
Тогда его проекция на оси координат будет:
, , .
Если существует предел отношения , то он называется Производной функции в точке По направлению и обозначается символом , т. е.
или .
Теорема. Если функция дифференцируема в точке , то она имеет в этой точке производную по любому направлению , причем
.
Доказательство. Функция дифференцируема, поэтому
(т. к. , , и ).
В частности, если , то и .
Аналогично при , и при .
В случае функции двух переменных вектор будет лежать в плоскости , поэтому формула для производной по направлению будет иметь следующий вид:
.
Так как в плоскости , , то справедлива также формула
.
Если частные производные и представляют собой скорость изменения функции вдоль соответствующей оси координат, то Производная по направлению выражает скорость изменения функции по отношению к величине перемещения точки В направлении вектора .
В частности, если , то плоскость, проходящая через точку и вектор параллельно оси , пересечет поверхность по некоторой кривой . В этом случае скорость изменения функции в направлении вектора будет численно равна тангенсу угла , образованного касательной к кривой в точке , соответствующей точке , и вектором . При она будет выражать крутизну возрастания функции в направлении вектора , а при — крутизну убывания.
Таким образом, производная по направлению оказывается весьма полезной при исследовании поведения функции в окрестности заданной точки.
Пример 15. Найти производную функции в точке по направлению от точки в точке .
Решение. Найдем вектор и соответствующий ему единичный вектор :
.
Таким образом, вектор имеет следующие направляющие косинусы , .
Теперь найдем частные производные функции :
,
,
И их значения в точке :
,
.
Подставляя в формулу найденные значения частных производных и направляющих косинусов, получим искомую производную функции по направлению вектора :
.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
72. Производная по направлению | Решение задач по математике и другим п
Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М1( x + Dx, y + Dy, z + Dz).
Проведем через точки М и М1 вектор . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются Направляющими косинусами Вектора .
Расстояние между точками М и М1 на векторе обозначим DS.
Высказанные выше предположения, проиллюстрируем на рисунке:
 z
z
M
M1
y
x
Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:
,
Где величины e1, e2, e3 – бесконечно малые при .
Из геометрических соображений очевидно:
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
;
Заметим, что величина s является скалярной. Она лишь определяет направление вектора .
Из этого уравнения следует следующее определение:
Определение: Предел называется Производной функции U(X, Y, Z) по направлению вектора В точке с координатами ( x, y, z).
Поясним значение изложенных выше равенств на примере.
Пример. Вычислить производную функции z = x2 + y2x в точке А(1, 2) по направлению вектора . В (3, 0).
Решение. Прежде всего необходимо определить координаты вектора .
=(3-1; 0-2) = (2; -2) = 2.
Далее определяем модуль этого вектора:
=
Находим частные производные функции z в общем виде:
Значения этих величин в точке А :
Для нахождения направляющих косинусов вектора производим следующие преобразования:
=
За величину принимается произвольный вектор, направленный вдоль заданного вектора, т. е. определяющего направление дифференцирования.
Отсюда получаем значения направляющих косинусов вектора :
Cosa = ; cosb = —
Окончательно получаем: — значение производной заданной функции по направлению вектора .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
