Определить простоту числа онлайн
На этой странице рассмотрим задачи while22 и while23 задачника Абрамяна: определение простоты числа и задача о нахождении наибольшего общего делителя соответственно. Ниже есть форма для проверки числа на простоту, для этого нужно ввести целое положительное число в жёлтое поле и нажать «проверить».
While22. Дано целое число N (> 1). Если оно является простым, то есть не имеет положительных делителей, кроме 1 и самого себя, то вывести true, иначе вывести false.
Код Pascal
|
While23. Даны целые положительные числа A и B. Найти их наибольший общий делитель (НОД), используя алгоритм Евклида:
НОД(A, B) = НОД(B, A mod B), если B ≠ 0; НОД(A, 0) = A,
где «mod» обозначает операцию взятия остатка от деления.Решение этой задачи смотрите на странице наибольший общий делитель.
progmatem.ru
Проверка числа на принадлежность его к простым числам
Простые числа — это натуральные числа, которые делятся только на единицу и на себя. В математике простые числа занимают особое значение.
Простые числа
Именно такие простые числа, которые нельзя разложить на множители, и являются атомами математики. Как и атомы химических элементов создают все вещества во Вселенной, так и неделимые формируют составные числа. Любое составное целое число мы можем разложить на произведение простых делителей, причем делители могут определяться разными методами, но результат всегда будет один и тот же.
Поиск простых чисел
Распределение простых чисел — это открытая проблема математики. Мы до сих пор не располагаем формулой для определения неделимых и не знаем доказанных закономерностей их распределения в ряду натуральных чисел. Магия цифр очаровывала ученых с античных времен, и первый метод поиска неделимых разработал Эратосфен Киренский. Древнегреческий ученый выстроил все натуральные числа в ряд, подчеркнул двойку и начал методично вычеркивать числа, которые делятся на 2. Затем он подчеркнул тройку и вычеркнул все числа, кратные 3 и так далее. Таким трудоемким способом он вычеркнул все составные числа из ряда, а оставшиеся неделимые составили так называемое решето Эратосфена.
При помощи решета мы можем определить простоту небольших чисел, однако как мы определим неделимость, к примеру, числа 58 467 или 58 477? Исключая 2 и 5, большинство простых чисел должны заканчиваться на 1, 3, 7, но это недостаточное условие. Числа выше тому подтверждение, 58 467 — составное число, раскладываемое на 3 и 19 489. А вот 58 477 — неделимое. Для решения подобных задач используется факторизация числа, однако для слишком больших чисел такой способ требует огромных вычислительных мощностей.
Самое большое простое число
Согласно гипотезе Евклида, простые числа устремляются в бесконечность. Современные математики бьются над поиском самого большого неделимого, однако с каждым годом открываются все большие и большие числа. На сегодняшний день самым большим простым числом является число Мерсенна М74207281, которое представляет собой 2n – 1, где n = 74207281. Это чудесное число содержит 22 338 618 цифр, а его запись занимает объем, равный семи романам «Война и мир». Ученые работают именно с числами Мерсенна, то есть числами вида 2n – 1, так как они эффективно проходят тест Люка — Лемера — тест простоты, разработанный для проверки чисел на принадлежность к неделимым.
Использование простых чисел
Помимо теории чисел, наиболее очевидной сферой применения неделимых является криптография и защита информации. Большие простые числа используются в криптографических алгоритмах шифрования данных и при создании электронных цифровых подписей. В мире информационных технологий простые числа являются фундаментом информационной безопасности.
Проверка на простоту
Наш калькулятор позволяет проверить на делимость любое целое число от 0 до 9 999 999. Введя переменную в окно калькулятора, вы получите ответ в виде принадлежности числа к простому или составному типу, а также два ближайших неделимых.
Пример из реальной жизни
Школьная задача
В учебниках по арифметике вам могут встретиться задачи на определение наименьшего общего кратного или наименьшего общего делителя. Для решения подобных задач используется метод разложения составного числа на простые множители. Если в задачах будут заданы достаточно большие числа, то прежде чем искать множители, рационально будет проверить число на делимость. Для этого и используйте наш калькулятор. К примеру, вам требуется найти НОК для пары 10628 и 15727. Если 10628 достаточно просто разложить на делители 2 × 2 × 2657, то число 15727 — простое, следовательно, задача не имеет решения.
Заключение
Неделимые — удивительные осколки, разбросанные в океане чисел. Мы только исследуем их природу и ищем способы проверки на неделимость поистине огромных чисел. Ну а для проверки небольших неделимых используйте наш калькулятор — быстрый и удобный инструмент для определения простоты чисел.
bbf.ru
СРАВНИТЕЛЬНЫЙ АНАЛИЗ АЛГОРИТМОВ ОПРЕДЕЛЕНИЯ ПРОСТОТЫ ЧИСЛА
В данной работе рассматриваются основные алгоритмы определения простоты числа. Мы сравним их, используя различные критерии, и определим наиболее оптимальный из них. Наконец, мы предложим программную реализацию самого эффективного и распространённого алгоритма.
Основные определения
Введем некоторые определения, которые будут использованы в работе.
Определение 1. Простое число – натуральное (целое положительное) число ℕ, которое имеет ровно два различных натуральных делителя – единицу и самого себя.
Определение 2. Составное число – натуральное (целое положительное) число ℕ, которое не является простым.
Определение 3. Тест простоты – алгоритм, который по заданному натуральному числу ℕ позволяет точно или с некоторой долей вероятности определить, является ли это число простым.
Определение 4. Криптография – наука о методах обеспечения конфиденциальности, целостности данных, аутентификации, а также невозможности отказа от авторства.
Определение 5. НОД(a,b) = d, d-наибольший общий делитель, если
1)
2)
Введение
Дискретная математика — важнейшее направление современной математики. Задачи этой дисциплины являются одними из самых трудноразрешимых. Например, решение задачи факторизации, которая заключается в разложении числа на простые множители, на практике сводится к поиску простых чисел, что приводит к проблеме простоты.
Постановка проблемы
Проблема определения простоты числа интересна с научной точки зрения, так как на данный момент не найдено единой аналитической записи для всех простых чисел. С другой стороны, большие простые числа применяются в криптосистемах с открытым ключом, и вопрос определения простоты числа является нетривиальной задачей. Простые методы, такие, как метод перебора, неприменимы для использования на практике из-за того, что требуют много вычислительных и временных ресурсов. Таким образом использование эффективного теста простоты позволяет повысить скорость и надежность алгоритмов в криптографии.
Тесты простоты
Следует отметить, что существующие алгоритмы проверки простоты могут быть разделены на две больших категории: истинные (детерминированные) и вероятностные тесты. Алгоритмы первой категории позволяют точно определить простоту или составность числа. А те, что относятся ко второй категории, позволяют это выяснить, но с некоторой вероятностью ошибки. Многократное их повторение для одного числа, но с разными параметрами, обычно позволяет сделать вероятность ошибки сколь угодно малой величиной.
Перебор делителей
Тип теста: детерминированный
Сложность алгоритма:
Описание: алгоритм тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.
Алгоритм: представлен на рисунке 1 в виде блок-схемы.
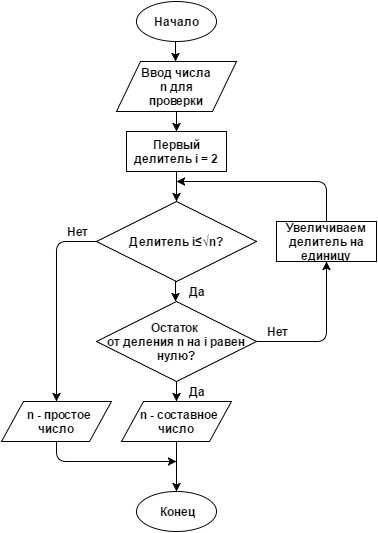
Рисунок 1. Алгоритм проверки числа на простоту при помощи перебора делителей.
Практическое применение: в чистом виде не используется из-за сравнительно большой вычислительной сложности. Деление на маленькие простые числа используется как один из шагов во многих тестах.
Теорема Вильсона
Тип теста: детерминированный
Сложность алгоритма:
Описание: натуральное число n > 1— простое число тогда и только тогда, когда (mod n)
Алгоритм: представлен на рисунке 2 в виде блок-схемы.
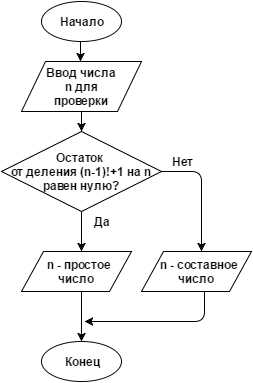
Рисунок 2. Алгоритм проверки числа на простоту при помощи теоремы Вильсона
Практическое применение: не применяется из-за трудности вычисления
(n-1)! при больших числах n.
Тест Агравал—Кайал—Саксена (AKS)
Тип теста: детерминированный
Сложность алгоритма:
Описание: единственны полиномиальный детерминированный алгоритм проверки числа на простоту. Если существует такое что и для любого a от 1 до выполняется сравнение то n – либо простое число, либо степень простого числа.
Алгоритм: представлен на рисунке 3 в виде блок-схемы.
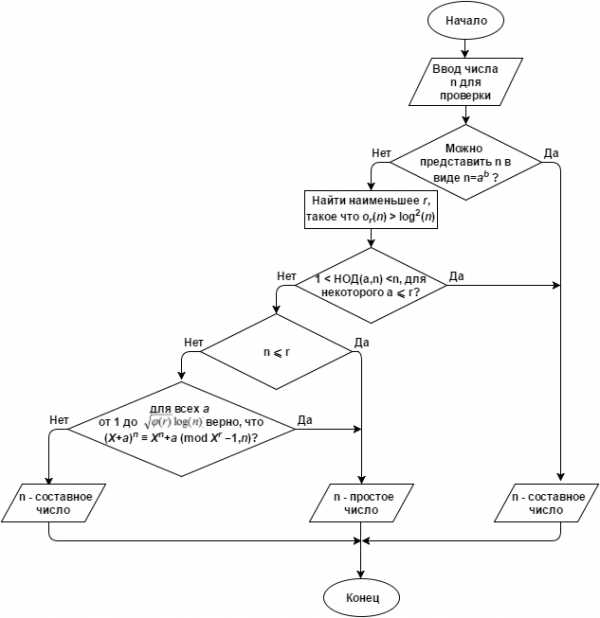
Рисунок 3. Алгоритм проверки числа на простоту при помощи теста AKS
Практическое применение: в качестве детерминированной полиномиальной проверки на простоту.
Критерий Поклингтона
Тип теста: детерминированный
Сложность алгоритма:, где с – положительная константа, , зависящие от выбора алгоритма факторизации.
Описание: пусть n – натуральное число и n-1 имеет простой делитель q, причем . Если найдется целое число a, для которого выполняются условия:
1.(mod n)
2. НОД(
Тогда n является простым числом.
Алгоритм: представлен на рисунке 4 в виде блок-схемы.
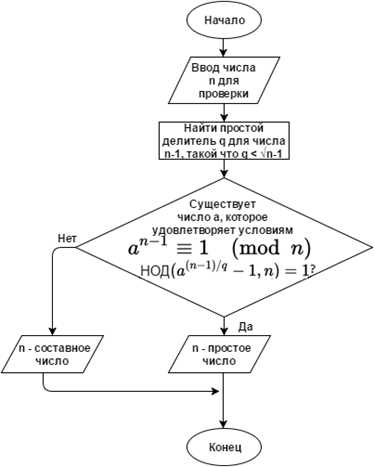
Рисунок 4. Алгоритм проверки числа на простоту при помощи критерия Поклингтона
Практическое применение: для получения больших простых чисел с частично известной факторизацией n – 1.
Тест Ферма.
Тип теста: вероятностный
Сложность алгоритма: O(log2n × loglog n × logloglog n)
Описание: тест простоты, основанный на малой теореме ферма, которая гласит, что если n – простое число, то для любого целого a выполняется равенство
или делится на нацело.
Алгоритм: представлен на рисунке 5 в виде блок-схемы.
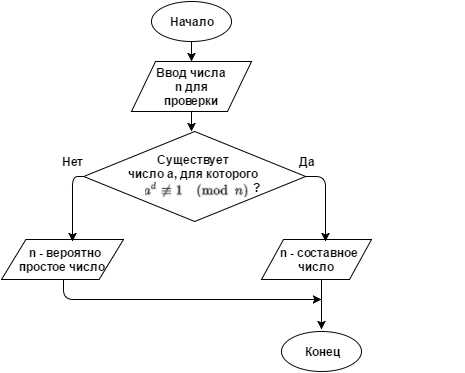
Рисунок 5. Алгоритм проверки числа на простоту при помощи теста Ферма.
Практическое применение: в чистом виде не используется. Лежит в основе многих алгоритмов проверки простоты числа.
Тест Миллера-Рабина
Тип теста: вероятностный
Сложность алгоритма: O(k*log2n), k–количество раундов
Описание: пусть n > 2 – натуральное число, тогда представим число n-1 в виде
n-1 = *t , где t – нечетно, а s — неотрицательно. Число a является свидетелем простоты для числа n, если выполняется одно из условий:
или . Количество свидетелей простоты увеличивают достоверность алгоритма.
Алгоритм: представлен на рисунке 6 в виде блок-схемы.
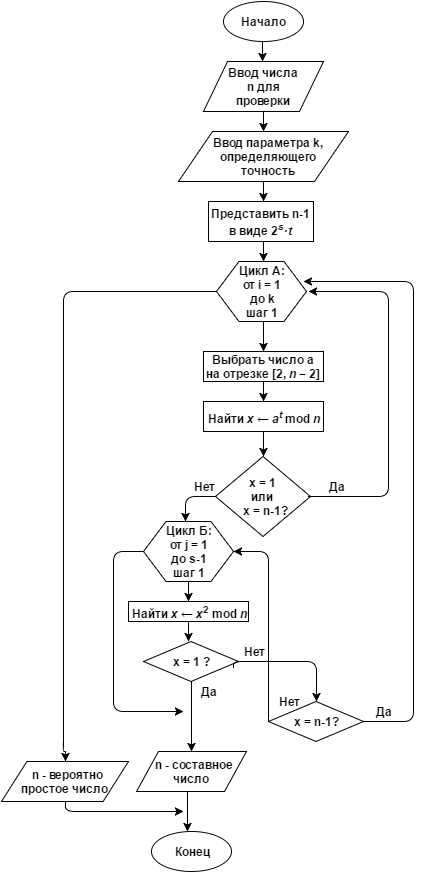
Рисунок 6. Алгоритм проверки числа на простоту при помощи теста Миллера-Рабина.
Практическое применение: используется в криптосистемах с открытым ключом. Позволяет проверить число на простоту за малое время и давать при этом малую вероятность того, что оно окажется псевдопростым.
Тест Соловея — Штрассена
Тип теста: вероятностный
Сложность алгоритма: O(log3n)
Описание: данный алгоритм характеризуется числом итераций k. В каждой итерации выбирается случайное число a < n. Если НОД (a, n) > 1, то число n — составное. В противном случае нужно выяснить, справедливо ли сравнение (mod n). Если сравнение не выполняется, то число n — составное. Если оно выполняется, то a – свидетель простоты числа n. Далее следует повторить данную процедуру, используя другое случайное число a. После нахождения количества свидетелей простоты k (число итераций) можно предположить, что n является простым числом с вероятностью .
Алгоритм:

Рисунок 7. Алгоритм проверки числа на простоту при помощи теста Соловея-Штрассена.
Практическое применение: не используется из-за недостаточной степени достоверности.
Сравнение тестов простоты
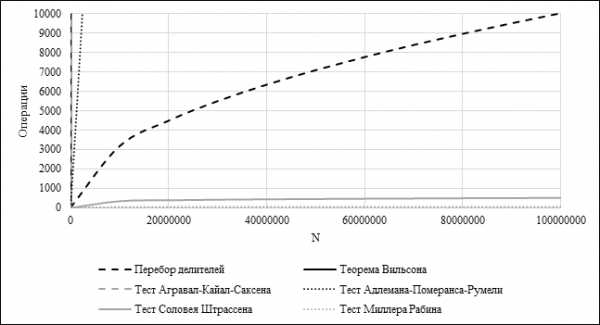
Рисунок 8. Сравнение алгоритмов проверки числа на простоту
Была проведена сравнительная характеристика различных алгоритмов определения простоты числа, по результатам которой можно построить график (рисунок 8). Нетрудно заметить, что среди тестов, которые подверглись проверке на быстродействие, самым эффективным оказался тест Миллера-Рабина. Рассмотрим его программную реализацию в виде консольного приложения.
Программная реализация теста Миллера-Рабина
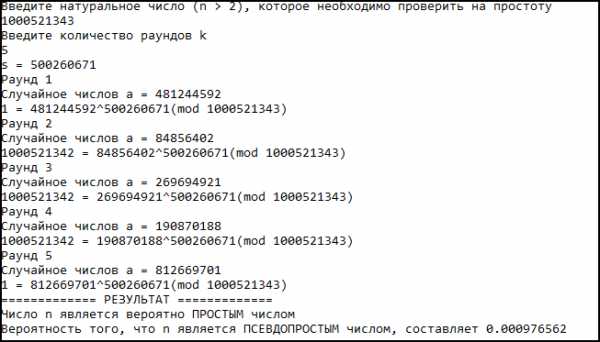
Рисунок 9. Демонстрация программной реализации алгоритма Миллера-Рабина.
Заключение
Подводя итоги, можно констатировать, что были изучены различные алгоритмы определения простоты числа и осуществлён их сравнительный анализ. Проведённые исследования позволяют сделать вывод о том, что тест Миллера-Рабина является наиболее эффективным и универсальным из тех, что были рассмотрены в данной статье.
Список литературы:
- Додонова Н.Л. Конспект лекций по дисциплине алгебраические структуры и теория чисел. Самара, 2016
- Шнайер, Б.М. Прикладная криптография/ Б.М.Шнайер — ТРИУМФ 2002. – 816 с.
sibac.info
Проверка простых чисел | Защита информации
Общее
В данной статье вы увидите обзор известных алгоритмов проверки чисел на простоту. На сегодня не существует единого алгоритма для определения всех простых чисел. Все методы проверки делят на две группы: вероятностные проверки и детерминированные. Детерминированные методы определяют точно, является ли число простым. Вероятностные проверки определяют число на простоту с некой вероятностью ошибки. Многократное повторение для одного числа, но с разными переменными, разрешает сделать вероятность ошибки сколь угодно малой величины.
Быстрые тесты для малых чисел и вероятно простые числа
Малые простые числа
Пока не было нужды в генерации больших простых чисел, можно было реализовывать методы проверки без применения вычислительной техники. Первым из таких методов является полный перебор всех возможных делителей. Есть модификация, которая не хуже всего перебора, называется — пробное деление. Он заключается в делении на предыдущие простые числа либо равные корню из этого числа. Для такого метода можно использовать решето Эратосфена.
Малая теорема Ферма
Французский математик Пьер Ферма в 17 веке выдал закономерность, которая лежит в основе почти всех методов проверки на простоту.
Малая теорема Ферма — Если P простое и A — любое целое, то AP = A (mod P). Если P не делит А, то АP-1 = 1 (mod P). На основе такой теоремы, можно создать мощный алгоритм на простоту:
- Тест Ферма: Для n > 1 выбираем a > и вычисляем An-1 mod n, если результат не 1, то n составное число, если 1, то n — слабо возможно простое по основанию a (a-PRP)
Часть чисел проходящие Тест Ферма являются составными, и их называют псевдопростыми.
Тест Рабина-Миллера
Можно улучшить тест Ферма, заметив, что если n — простое нечетное, то для 1 есть только два квадратных корня по модулю n: 1 и -1. По этому квадратный корень из An-1, A(n-1)/2 равен минус или плюс еденице. Если (n-1)/2 опять нечетно, то можно снова извлечь корень и тд. Первый вариант алгоритма определяет только одно деление:
- Тест Леманна: Если для любого целого числа А меньшего n не выполняется условие A(n-1)/2 = ± 1 (mod n), то число n — составное. Если это условие выполнено, то число n — возможно простое с вероятностью ошибки не больше 50%.
- Тест Рабина-Миллера: Запишем (n-1) в виде 2sd, где d нечетно, а s — неотрицательно: n называют сильно возможно простым по основанию A (A-SPRP), если реализуется одно из двух условий:
- Ad = 1 (mod n)
- (Ad)2r = -1 (mod n), для любого неотрицательного r < s
В 1980 году была доказана вероятность ошибки теста Рабина-Миллера не превышающая 1/4. Реализуя этот тест T раз для разных оснований, мы получим вероятность ошибки 2-2t
Объединение тестов
Классические тесты
Проверки чисел вида n + 1
Тест заключается в том, что мы должны знать частичное или полное разложение на множители числа n — 1. Разложение на множители n — 1 просто найти, если n имеет определенный вид.
- Тест Лукаса: N ≥ 3. Если для каждого простого q, делящего n — 1 есть целое А такое что:
- An-1 = 1 (mod n) и
- A(n-1)/q ≠ 1 (mod n), то n — простое
Для такой проверки нужно знать полное разложение n — 1 на простые множители. Более мощная версия определяет знание не полного, а частичного разложения n — 1 на простые множители. Такой вариант алгоритма был выдан Поклингтоном в 1914 году.
- Тест Поклингтона: N ≥ 3 и n = FR + 1 (F делит n-1), причем F > R, НОД (F,R) = 1 и известно разложение F на простые множители. Тогда, если для любого простого q, делящего F есть такое целое A > 1, что:
- An-1 = 1 (mod n) и
- НОД (A(n-1)/q — 1, n) = 1
- Теорема Пепина: пусть Fn это n-е число Ферма и n > 1, тогда Fn — простое тогда и только тогда, когда 3(Fn — 1)/2 = 1 (mod Fn
- Теорема Прота: Пусть n = h × 2k + 1, причем 2k > h. Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
На основе теоремы Прота было найдено пятое по величине из известных простых чисел — 28433 × 27830457
Проверки чисел вида n — 1
Здесь рассмотрим числа только определенного вида. 7 из первых 10 позиций по самым большим известным простым числам были найдены с помощью чисел Мерсенна. Числа Мерсенна называют числа вида 2s -1.
Лукасом и Лемером в 1930 году было создано следующее утверждение: пусть s — простое, тогда число Мерсенна n = 2s — 1 является простым тогда, когда S (n — 2) = 0, где S(0) = 4 и S(k+1) = S(k)2 — 2 (mod n). На основе такого факта можно создать проверку на простоту, которая точно скажет нам, является ли для заданного s число Мерсенна простым.
- Тест Лукаса-Лемера:
- С помощью пробного деления проверяем, является ли данное s простым, если нет, то получившееся число Мерсенна — составное
- Задаем S(0) = 4
- Для k от 1 до s — 2 вычисляем S(k) = S(k-1)2 — 2 (mod n)
- Если в результате получился 0, то число Мерсенна простое
Неоклассические алгоритмы ARP и ARP-CL
Можно рассматривать числа в виде n2 + n + 1 или n2 — n + 1. А можно рассмотреть число вида nm — 1 для больших m. Тогда любое просто число q такое, что q — 1 делит m, по малой теореме Ферма будет делить nm — 1.
Было представлено, что всегда существует целое число m:
Эллиптические кривые: ECPP
Современные вариант проверок на простоту основан на теореме Поклингтона, но для эллиптических кривых. Смысл алгоритма заключается в переходе от групп порядка n — 1 и n + 1 к достаточно большему диапазону размеров групп.
AKS
В 2002 году летом индийские математики Аграавал, Саксен и Кайал нашли полиномиальный детерминированный алгоритм проверки числа на простоту. Их метод основан на версии малой теоремы Ферма:
- Теорема: Пусть A и P взаимно простые целые числа и P > 1. Число P является простым, когда (x — a)p = (xp — a) (mod p)
- Доказательство: Если p — простое, то p делит биномиальные коэффициенты pCr для r = 1,2 ..p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
if (n is has the form ab with b > 1) then output COMPOSITE
r := 2
while (r < n) {
if (gcd(n,r) is not 1) then output COMPOSITE
if (r is prime greater than 2) then {
let q be the largest factor of r-1
if (q > 4sqrt(r)log n) and (n(r-1)/q is not 1 (mod r)) then
break
}
r := r+1
}
for a = 1 to 2sqrt(r)log n {
if ( (x-a)n is not (xn-a) (mod xr-1,n) ) then output COMPOSITE
}
output PRIME;
Итоги
| Тест | Тип теста | Где используется |
|---|---|---|
| Пробное деление | детерминированный | Из-за большой вычислительной сложности в чистом виде не используется. Пробное деление на маленькие простые числа реализуется во многих тестах как один из шагов |
| Ферма | вероятностный | В чистом виде не реализуется. Может быть одним из первых шагов на проверку простоты для очень больших чисел |
| Леманна | верляьнлсьный | Не используется |
| Рабина-Миллера | вероятностный | В чистом виде может реализовываться в криптосистемах с открытым ключом для реализации простых ключей длиной 512, 1024 и 2048 бит. |
| Миллера | детерминированный | На практике не используется, так как пока не доказана расширенная гипотеза Римана |
| Лукаса | детерминированный | Для получения больших простых чисел определенного вида |
| Поклингтона | детерминированный | Для получения больших чисел с частично известной факторизацией n — 1 |
| Петина | детерминированный | Для получения больших простых чисел Ферма |
| Прота | детерминированный | Для получения больших простых чисел определенного вида |
| Лукаса-Лемера | детерминированный | Для получения больших простых чисел Мерсенна |
| APR | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| ECPP | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| AKS | детерминированный | В качестве детерминированной полиномиальной проверки на простоту |
Из таблицы видно, что разные методы проверки на простоту служат для двух целей:
- для получения очень больших целый чисел
- для генерации простых чисел определенного размера для реализации в криптографии
Аналитическую работу провел студент (ГУ МФТИ) кафедры радиотехники Кучин Борис.
infoprotect.net
Как проверить простое ли число
Автор КакПросто!
Теория простых чисел волнует математиков многие века. Известно, что их бесконечное множество, но тем не менее до сих пор не найдено даже формулы, которая давала бы одни простые числа.

Статьи по теме:
Инструкция
Пусть по условию задачи вам задано число N, которое необходимо проверить на простоту. Для начала убедитесь, что N не имеет самых тривиальных делителей, то есть не делится на 2 и 5. Для этого проверьте, что последняя цифра числа не равна 0, 2, 4, 5, 6 или 8. Таким образом, простое число может заканчиваться лишь на 1, 3, 7 или 9. Просуммируйте цифры числа N. Если сумма цифр делится на 3, то само число N будет делиться на 3 и, следовательно, не является простым. Походим образом проверяется делимость на 11 — надо просуммировать цифры числа с переменой знака, поочередно суммируя или вычитая каждую следующую цифру из результата. Если результат будет делиться на 11 (или равняться нулю), то и исходное число N делится на 11. Пример: для N = 649 знакопеременная сумма цифр М = 6 — 4 +9 = 11, то есть это число делится на 11. И действительно, 649 = 11·59. Введите свое число на сайте http://www.usi.edu/science/math/prime.html и нажмите кнопку “Check my number”. Если число простое, программа напишет что-то вроде “59 is prime”, а иначе представит его в виде произведения множителей. Если обратиться к интернет-ресурсам по какой-то причине возможности нет, придется решать задачу перебором множителей — существенно более эффективного метода до сих пор не найдено. Вам нужно перебрать простые (либо все) множители от 7 до √N и попытаться произвести деление. N окажется простым, если ни на один из этих делителей не разделится нацело.Чтобы не заниматься перебором вручную, можно написать собственную программу. Вы можете воспользоваться любимым языком программированию, скачав для него математическую библиотеку, в которой есть функция определения простых чисел. Если библиотека вам недоступна, придется действовать перебором, как описано в пункте 4. Удобнее всего перебирать числа вида 6k±1, так как все простые числа кроме 2 и 3 представимы в таком виде.
www.kakprosto.ru
