Модуль в выражениях – Как решать уравнения с модулем

Содержание

Модуль

Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.
\(|a|=\begin{cases} a, \;\; если \; a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\; a<0 \end{cases}\)

Второе название модуля – «абсолютное значение действительного числа».

Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:

— если подмодульное выражение положительно, модуль просто убирается. При этом само выражение не меняется.

— если же оно отрицательно, то при снятии модуля перед подмодульным выражением надо добавить знак «минус», чтобы сделать его положительным.

Об этом правиле нужно помнить при работе с более сложными выражениями или

выражениями, содержащими переменные.

Пример. Раскрыть \(|\sqrt5-3|\)

Решение: Под модулем отрицательное выражение (т.к. \(\sqrt 5 \approx 2,24\), то есть меньше \(3\)). Значит, раскрывать модуль надо добавляя минус перед выражением:

Ответ: \(3-\sqrt 5\)

Пример. Раскрыть \(|x^4+1|\)

Решение: т.к. \(x^4+1\) больше нуля при всех значениях \(x\), то \(|x^4+1|=x^4+1\).

Ответ: \( x^4+1\)

Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).

Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):

\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)

Ответ: \(-10\)

Геометрическое определение модуля

\(|a|\) — это расстояние от \(0\) до числа \(a\) на числовой оси

Пример. Чему равен \(|5|\) и \(|-5|\)?

Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).

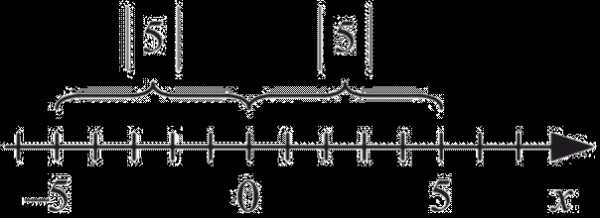
Значит ответ: \(|5|=5\), \(|-5|=5\).

Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.

Понимать легче второе определение, но практике удобнее использовать первое.

Решение простейших уравнений с модулем

Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности \( \left[ \begin{gathered}f= g\\ f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).

Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.

Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.

Пример. Решить уравнение:

\(\|x-1\|=3x\)		Найдем ограничения уравнения. Запишем его немного правее от основного решения
\(3x≥0\) \(x≥0\)		Когда ограничение записано — можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений
\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\)		Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо»
\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right.\)		Приведем подобные слагаемые
\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\)		Поделим первое уравнение на \(-2\), второе на \(4\).
\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\)		Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ

Ответ: \(\frac{1}{4}\)

Решение простейших неравенств с модулем

Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству \( -c< f< c\) , при условии, что \(c>0\).

Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!

Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).

Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).

А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.

Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).

\(\|3x-7\|≤8\)		\(\|3x-11\|≥11\)
\(-8≤3x-7≤8\) \(\|+7\)		\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\)
\(-1≤3x≤15\)		\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\)
\(-\frac{1}{3}≤x≤5\)		\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right.\)
Ответ: \([ -\frac{1}{3};5]\)		Ответ: \( (-\infty;0]\cup [ \frac{22}{3};\infty)\)

Смотрите также:
Свойства модуля

cos-cos.ru

Как извлечь из модуля 🚩 как раскрывать модуль 🚩 Математика

Инструкция

Если под знаком модуля находится число, значение которого вам известно, то раскрыть его очень просто. Модуль числа a, или |a|, будет равен самому этому числу, если a больше либо равно 0. Если a меньше нуля, то есть является отрицательным, то его модуль будет равен противоположному ему, то есть |-a|=a. Согласно этому свойству, модули противоположных чисел равны, то есть |-a|=|a|. В том случае, если подмодульное выражение возведено в квадрат или в другую четную степень, то можно просто опустить скобки модуля, так как любое число, возведенное в четную степень, является неотрицательным. Если нужно извлечь квадратный корень из квадрата числа, то это также будет модуль этого числа, поэтому модульные скобки можно опустить и в этом случае.

Если в подмодульном выражении имеются неотрицательные числа, то их можно вынести за пределы модуля. |c*x|=c*|x|, где с – неотрицательное число.

Когда имеет место уравнение вида |x|=|c|, где x является искомой переменной, а c действительным числом, то раскрыто оно должно быть следующим образом: x=+-|c|.

Если нужно решить уравнение, содержащее модуль выражения, результатом которого должно быть вещественное число, то знак модуля раскрывают, исходя из свойств этой неопределенности. К примеру, если имеется выражение |x-12|, то, если (x-12) – неотрицательное, оно останется неизменным, то есть модуль раскроется как (x-12). Но |x-12| превратится в (12-x), если (x-12) меньше нуля. То есть, модуль раскрывается в зависимости от значения переменной или выражения в скобках. Когда знак результата выражения неизвестен, то задача превращается в систему уравнений, первое из которых рассматривает возможность отрицательного значения подмодульного выражения, а второе – положительного.

Иногда модуль можно однозначно раскрыть, даже если его значение неизвестно по условиям задачи. Например, если под модулем находится квадрат переменной, то результат будет положительным. И наоборот, если там заведомо отрицательное выражение, то модуль раскрывается с противоположным знаком.

www.kakprosto.ru

Понятие модуля числа и алгебраических выражений

« Модуль числа и алгебраического выражения. Линейные уравнения, содержащие модуль»

Что такое модуль?

Слово «модуль » произошло от латинского слова «modulus», что в переводе означает «мера ».
Это многозначное слово , которое имеет множество значений и применяется не только в математике, но и в физике, технике, программировании и других точных науках.
В технике – это термин служит для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости.
В физике — это модуль объемного сжатия, отношение нормального напряжения в материале к относительному удлинению.

Понятия и определения.

Уравнение – это равенство, содержащее переменные.

Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например: | х | = 1
Решить уравнение – это значит найти все его корни, или доказать, что корней нет.
Модуль – расстояние от начала отсчета до точки на числовой прямой.

0; | а |= — а, если а Из определения следует, что для любого действительного числа а, | а | 0 и | -а | = | а |. «

Определение модуля числа.

Модуль – это расстояние от начала отсчета до точки на числовой прямой.

А это значит:

Модуль числа а равен а, если а больше или равно нулю и равен – а, если а меньше нуля :

а, если а 0; | а |= — а, если а

Из определения следует, что для любого действительного числа а,

| а | 0 и | -а | = | а |.

Примеры:

│ 5│= 5
│ 2- 6│= — (- 4)=4 так как (2-6) – число отрицательное.
│ -8│= -(- 8 )= 8 так как (-8) – число отрицательное.
│ 2-13│= -(-11)=11, так как (2-13) – число отрицательное.

0 или х = -а, если а׀ х — 5 ׀ = 6 х-5=6 х=11, х-5=-6 х=-1 ׀ 2 х+7 ׀ =- 4 ø решений нет. ׀ 7 х-49 ׀ = 0 7 х-49=0 7х=49 х=49:7 х=7 «

Решение уравнений:

׀ х ׀ = а х = а, если а0 или х = -а, если а
׀ х — 5 ׀ = 6 х-5=6 х=11, х-5=-6 х=-1
׀ 2 х+7 ׀ =- 4 ø решений нет.
׀ 7 х-49 ׀ = 0 7 х-49=0 7х=49 х=49:7 х=7

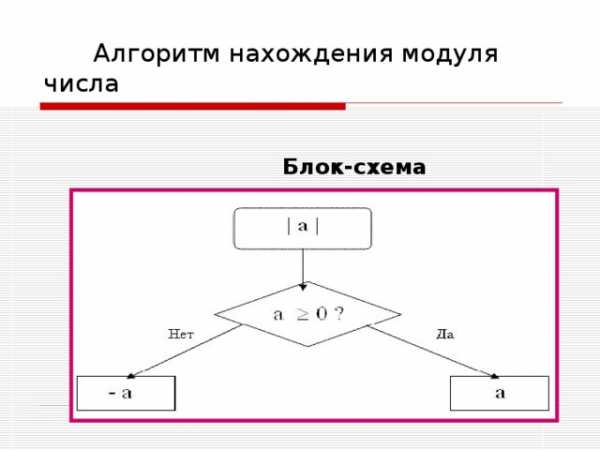
Алгоритм нахождения модуля числа

Блок-схема

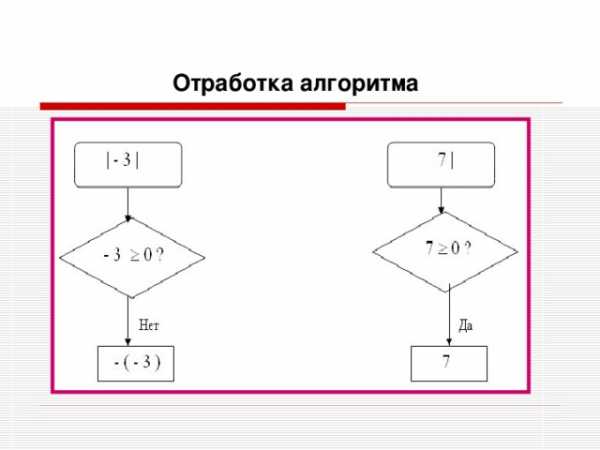
Отработка алгоритма

| 81 | = 81; | 1,3 | = 1,3; | – 5,2 | = 5,2;

| 8/9 | = 8/9; | – 5/7 | = 5/7; | – 2 9/25 | = 2 9 /25;

| – 52 | = 52; | 0 | = 0.

| – 8 | – | – 5 | = 8 – 5 = 3 | – 10 | . | – 15 | = 10 . 15 = 150 | 240 | : | – 80 | = 240 : 80 = 3 | 0,1 | . | – 10 | = 0,1 . 10 = 1

Примеры:

Задание 1

1 Найти значения выражений |-100| , |5+1,1| , |4,4- 8,9| , -|-9,7| , |5-16|

1 Найдите модуль числа _ 18 10 _ 16 9 2 4

2 Найдите положительное число модуль которого равен: 3 ; 5.

3. Известно,что |a|= 4

Чему равен |-a|?

|a|= 4,6 Чему равен |-a|?

|a|= 3,03 Чему равен |-a|?

4. Выберите из двух чисел, модуль которого меньше: -5 и 6 2 и -4 -2 и -3 5 Найдите значение выражения: |0,4| * |-2,5| |-40| * |0,1| |3,6| : |-1,2|

Задание 2

А. Заполни таблицу:

а) | – 8 | и | – 5 | б) | 12,3 | и |-11 | в) | 0 | и | –| 1,5 |

| х |

8,3

| х |+12

-8,3

1,5

| х | -1

-1,5

-105

Чтобы решить уравнение, содержащее переменную под знаком модуля, надо освободиться от знака модуля, используя его определение.

На практике это делают так….

Задание 3

| х – 6 | = 9
|2х + 3| = 3х –3.
|х + 5| – |х – 3| = 8.
|х + 2| + |х + 3| = х.
|2 + |2 + х|| = 3.
Д-З
|5х + 3| = 1
|2х — 3| = 1
|х — 5| + |2х –6| = 7

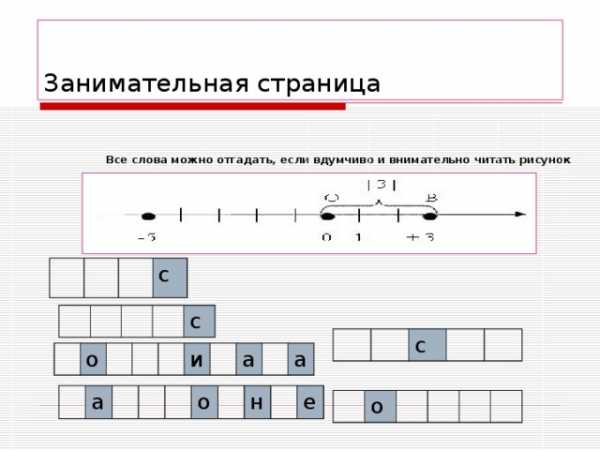
Занимательная страница

Все слова можно отгадать, если вдумчиво и внимательно читать рисунок

multiurok.ru

Как раскрыть модуль (условие в пояснениях )

Как уже вам говорили в предыдущих ответах, выражения под знаком модуля могут быть как положительны так и отрицательны. Давайте попробуем решить эти примеры. 1) положительны: (5х-10)-(3х+9)=5х-10-3х-9=2х-19; 2) отрицательны: -(5х-10)-(-(3х+9))=-5х+10+3х+9=-2х+19. Имеем два ответа.

число по модулю есть число либо положителное либо отрицательное, дальше всё просто, решай

Решается так же, как и без модуля, только ответ всегда положительный (если получилось отрицательное число по модулю)

на числовой прямой отмечаешь нули обоих выражений. => у тебя три промежутка. для каждого из них ставишь плюсы и минусы, по ним раскрываешь модули.

(5х — 10) — (3х + 9)= реши-это первые ответы (10-5х) -(3х+9)=реши и это вторые ответы ps: если я еще правильно помню модули…

5x-10 может быть положительным и отрицательным, тоже самое и с 3x+9 ну и решай

пишешь для каждого выражения под модулем два равенства: 5х-10=0 и 3х-9=0 получаются иксы равные 2 и 3,это значит, что если х<2 первое и второе выражение раскрывается со знаком минус, если 2<x<3,>3, то оба со знаком плюс, те 1)x<2 -2x+19 2)x принадлежит от 2 до 3 8х-1 3)x>3 2x-19

Если 5х больше нуля, то = 5х-10 Если 5х меньше нуля, то =10-5х Надо знать х положительное или отрицательное число

touch.otvet.mail.ru

Найти модуль с корнем — Науколандия

Как известно, модуль числа — это его абсолютное значение, без учета знака. Модуль всегда неотрицателен. Это значит, что он может быть равен либо положительному числу, либо нулю.

Таким образом, если дается положительное число или ноль, то их модуль будет равен им самим. А вот для отрицательного числа, его модуль будет иметь противоположное значение, т. е. являться противоположным числом. Так

|–3| = 3,
|–1,345| = 1,345.

Если представить числовую прямую (координатную прямую), то можно сказать, что на том расстоянии, на котором от нуля находится отрицательное число в одну сторону, на том же расстоянии от нуля находится его модуль, но в другую сторону.

Однако как найти модуль числового выражения, если его вычислить проблематично. Например, в выражениях с корнями когда получаются иррациональные числа. Пусть требуется найти модуль √2 – 2. Понятно, что здесь получится отрицательное число, т. к. 2 определенно больше √2. Следовательно, модулем этого выражения будет противоположное число. Но каково оно?

Чтобы получить противоположное число, надо умножить его на –1. Обычно просто приписывают к нему знак минуса. Если число отрицательное, то минус на минус дает плюс, и в результате получается положительное. Например, для –5 противоположное –(–5) = 5. Поэтому, когда берется модуль отрицательного числа, то можно не просто писать |–1,2| = |1,2|, а расписывать действие подробно:

|–1,2| = –(–1,2) = 1,2

Сделаем то же самое по отношению к выражению √2 – 2, коли мы уже знаем, что это отрицательное число:

|√2 – 2| = –(√2 – 2) = –√2 + 2 = 2 – √2

Таким образом, при вычислении модуля выражения с корнем следует придерживаться следующего алгоритма:

Определить, является ли число положительным или отрицательным.
Если число положительное или 0, то его модуль будет равен ему самому.
Если число отрицательное, то умножить его на –1, после чего преобразовать выражение к удобному виду.

Теперь обратим внимание на следующее. Выше было сказано, что модуль отрицательного числа отстоит от точки отсчета (нуля) на таком же расстоянии (но в другую сторону), как и само это число. Однако в примере с корнем мы видим, что само выражение и его модуль не выглядят такими уж идентичными по абсолютному значению. Трудно сказать, действительно ли √2 – 2 отстоит от нуля на таком же расстоянии как 2 – √2.

Однако это так. Если записать отрицательное число с корнем как –2 + √2, то понятно, что мы получаем число, которое больше –2, т. е. находится от –2 ближе к нулю на √2. Модуль же числа равен 2 – √2. Это число, которое меньше 2 на √2. То есть тоже находится от 2 ближе к нулю на √2.

scienceland.info