Прямая пропорциональность и ее график
График прямой пропорциональности
В 7 и 8 классе изучается график прямой пропорциональности.
Как построить график прямой пропорциональности?
Рассмотрим на примерах график прямой пропорциональности.
График прямой пропорциональности формула
График прямой пропорциональности представляет функцию прямая пропорциональность.
В общем виде прямая пропорциональность имеет формулу
y = kx
где k – коэффициент прямой пропорциональности.
От величины и знака коэффициента прямой пропорциональности зависит угол наклона графика прямой пропорциональности по отношению к оси икс.
График прямой пропорциональности проходит
График прямой пропорциональности проходит через начало координат.
График прямой пропорциональности есть прямая. Прямая задается двумя точками.
Таким образом при построении графика прямой пропорциональности достаточно определить положение двух точек.
Но одну из них мы всегда знаем – это начало координат.
Осталось найти вторую. Посмотрим пример построения графика прямой пропорциональности.
Постройте график прямой пропорциональности y = 2x
Задача.
Постройте график прямой пропорциональности, заданной формулой
y = 2x
Решение.
Область определения прямой пропорциональности есть все числа.
Берем любое число из области определения прямой пропорциональности, пусть это будет 1.
Найти значение функции при икс равное 1
y = 2x =
2 * 1 = 2
то есть при x = 1 получаем y = 2. Точка с этими координатами принадлежит графику функции y = 2x.
Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.
Одну из них мы только что нашли, а второй для прямой пропорциональности всегда является начало координат.
Теперь мы готовы построить график функции y = 2x.
Отмечаем на координатной плоскости точку с координатами (1; 2).
Через данную точку и начало координат проводим прямую линию
Мы получили график прямой пропорциональности, заданной формулой y = 2x.
www.sbp-program.ru
Основные правила преобразования графиков функций. Видеоурок. Алгебра 9 Класс
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции – это прямая, а график функции – это парабола. Но как построить, например, график функции , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси
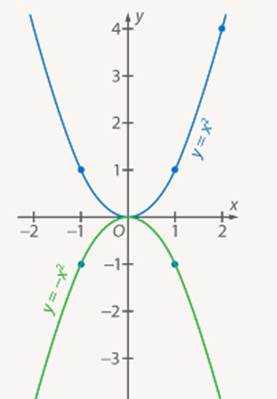
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой. График получается из графика функции преобразованием симметрии относительно оси .
На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше на 3 единицы. Графически это означает, что график функции находится на 3 единицы выше, чем график функции (см. Рис. 4).
Рис. 4. Графики функций и
График получается из графика функции параллельным переносом последнего вдоль оси ординат на единиц вверх, если , и на единиц вниз, если (см. Рис. 5, 6).
Рис. 5. Параллельный перенос вдоль оси (при )
Рис. 6. Параллельный перенос вдоль оси (при )
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше в 2 раза. Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).
Рис. 7. Графики функций и
Если необходимо построить график функций , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика меньше в 2 раза, чем у . Графически это означает, что график функции расширяется по сравнению с графиком функции (см. Рис. 8).
Рис. 8. Графики функций и
Чтобы построить график функции , где и , нужно ординаты точек заданного графика умножить на . Такое преобразование называется растяжением от оси с коэффициентом , если , и сжатием к оси, если (см. Рис. 9, 10).
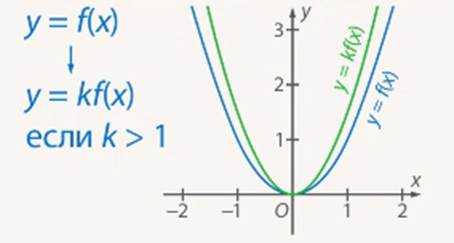
Рис. 9. Растяжение от оси

Рис. 10. Сжатие к оси
Предположим, что у нас есть функция , необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
, при
при
Следовательно, если необходимо было построить график функции , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции ) (см. Рис. 11).

Рис. 11. Графики функций , и
График получается из графика функции параллельным переносом последнего на единиц влево, если , и на единиц вправо, если (см. Рис. 12, 13).

Рис. 12. Параллельный перенос влево при
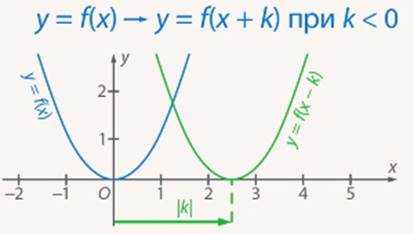
Рис. 13. Параллельный перенос вправо при
Обратите внимание на то, что по этому принципу из графика не построить график , ведь мы добавили 1 не ко всем вхождениям в это выражение. А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).

Рис. 14. Графики функции и
График функции , где и , получается из графика функции сжатием с коэффициентом к оси
Рис. 15. Сжатие к оси
Рис. 16. Растяжение от оси
Подобное преобразование мы уже рассматривали в случае построения графика функции .
Ранее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.
В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:
для функции :
при
при
для функции :
при
приГрафик получается из графика функции преобразованием симметрии относительно оси (см. Рис. 17).

Рис. 17. Преобразование симметрии относительно оси Oy
Построение графиков и
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси (см. Рис. 18).
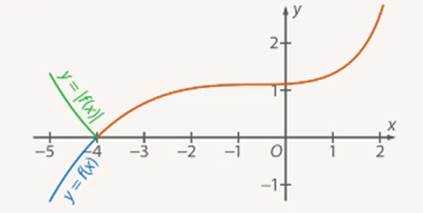
Рис. 18. Графики функций и (красным цветом выделена общая часть этих графиков)
Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, все точки с положительными или равными нулю абсциссами остаются без изменения, а все точки с отрицательными – заменяются точками с противоположными абсциссами (см. Рис. 19).
Рис. 19. Графики функций и (красным цветом выделена общая часть этих графиков)
Для того чтобы построить график , нужно часть исходного графика, соответствующую значениям , оставить без изменений и отразить ее относительно оси для значений .
Построить график функции .
Решение
Построим график заданной функции последовательно (см. Рис. 20):
1. Строим график .
2. График получается из графика параллельным переносом последнего на 2 единицы вправо.
3. График получается из графика функции параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
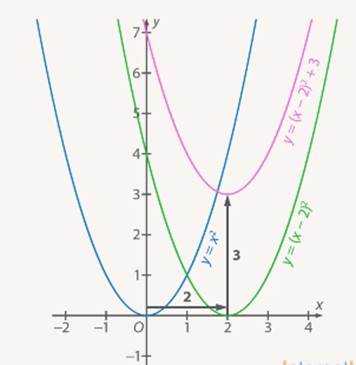
Рис. 20. Иллюстрация к задаче
Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).

Рис. 21. Иллюстрация к задаче
Обратите внимание, что не все графики функций можно строить в произвольном порядке. Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.
– ПРАВИЛЬНО
– НЕПРАВИЛЬНО
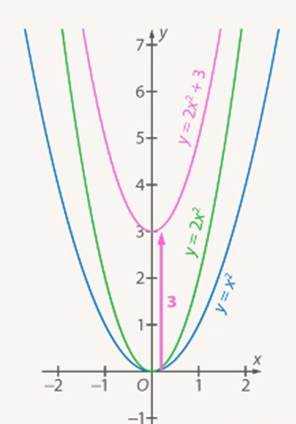
Рис. 22. Иллюстрация к задаче
Пример
Построить график .
Решение
1. Строим график (гипербола) (см. Рис. 23).
2. Строим график (из аргумента вычитается 2, следовательно, сдвигаем график на 2 единицы вправо) (см. Рис. 23).
3. Строим график (домножение функции на (-1), следовательно, отражаем график относительно оси ) (см. Рис. 24).
4. Строим график (добавление 2 к функции, следовательно, сдвигаем график на 2 единицы вверх) (см. Рис. 24).
5. Строим график (модуль функции, следовательно, отражаем нижнюю часть графика относительно оси , а верхнюю оставляем без изменений) (см. Рис. 25).

Рис. 23. Иллюстрация к задаче

Рис. 24. Иллюстрация к задаче
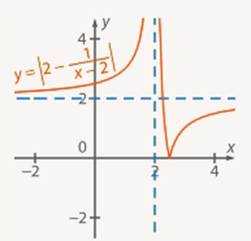
Рис. 25. Иллюстрация к задаче (искомый график)
Список литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений. – 4-е изд. – М.: Мнемозина, 2002. – 192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. – 4-е изд. – М.: Мнемозина, 2002. – 143 с.: ил.
3. Макарычев Ю.Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. – 7-е изд., испр. и доп. – М.: Мнемозина, 2008.
5. Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт учебного центра «Резольвента» (
interneturok.ru
Прямая пропорциональность и её график (В.А.Тарасов). Видеоурок. Алгебра 7 Класс
Напомним, что мы изучаем линейное уравнение относительно двух переменных – х и у, уравнение вида ,
Мы знаем, что графиком данного уравнения является прямая линия, каждая точка которой характеризуется двумя числами – координатами х и у – абсциссой и ординатой, и каждая точка удовлетворяет заданному уравнению.
В одном из уроков мы выражали у через х:
Пользуясь тем, что можем на него разделить обе части уравнения:
Для удобства приняли следующие обозначения: , получаем:
Таким образом, была получена линейная функция у от х в общем виде. Мы ввели некоторые новые обозначения: х называем независимой переменной, или аргументом, у называем зависимой переменной, или функцией. k и m – параметры, которые полностью и однозначно определяют конкретную линейную функцию.
Рассмотрим частный случай линейной функции, когда , в таком случае . Данная функция называется прямой пропорциональностью. Она определяется единственным параметром k. Нам следует изучить влияние данного параметра на график функции прямой пропорциональности и на саму функцию.
Рассмотрим примеры:
Пример 1:
Пусть известно, что турист двигается со скоростью 2 км/ч от некоторого пункта А к другому пункту В. В таком случае пройденный им путь будет подчиняться закону:
(1)
Если известно, что пассажир едет на поезде от некоторого пункта А к другому пункту В, а поезд движется со скоростью 60 км/ч, то в каждый момент времени можно определить удаление пассажира от начального пункта по формуле:
(2)
В общем виде обе эти формулы можно представить как . Не важно, что подразумевают под собой переменные х и у, важно только, что одна из них независимая, например время, а вторая зависимая, например расстояние.
Вернемся к нашим примерам. В общем виде формулы 1 и 2 можно представить как
Отсюда – это одна из физических интерпретаций углового коэффициента.
Если перейти к формуле прямой пропорциональности, то
Рассмотрим примеры:
Пример 2:
(3) и (4) – обе функции это прямая пропорциональность. Построим графики этих функций, для этого составим таблицы:
Таблица для функции 3;
Таблица для функции 4;

Угловой коэффициент является аналогом скорости в равномерном прямолинейном движении.
Одна из основных задач – это уметь находить угловой коэффициент в различных выражениях.
Пример 3 – найти угловой коэффициент:
Отсюда очевидно, что
Отсюда очевидно, что
Отметим также, что если , то угол между графиком функции и положительным направлением оси х тупой и функция убывает, а если k>0 – угол острый и функция возрастает, это видно из графика в примере 2. Физический аналог этому такой: если турист ушел из дома и его скорость равна 2км/ч, то в каждый момент времени расстояние от него до дома увеличивается, а если сказать, что расстояние выражается как , это значит, что он возвращается домой и расстояние сокращается.
Сформулируем свойства прямой пропорциональности:
— График любой такой прямой проходит через начало координат, так как в уравнении при независимо от значения у будет равен нулю;
— Рассмотрим несколько функций:
– прямая пропорциональность;
– линейная функция;
– линейная функция;
Построим графики данных функций. У каждой из них . У первой , у второй , у третьей . Напомним, что параметры k и m определяются из стандартного вида линейного уравнения
Составим таблицы для построения графиков:
Таблица для первой функции;
Таблица для второй функции;
Таблица для третьей функции;
Как мы видим, построенные прямые параллельны, причиной тому является равенство их угловых коэффициентов. Есть теорема, которая гласит:
Если – график прямой пропорциональности, то график будет ему параллелен, так как коэффициент k определяет угол наклона к оси х, и этот коэффициент у функций равный.
Пример 3 – построить графики функций:
Сразу отметим, что прямые не будут параллельны, так как их угловые коэффициенты не равны.
Для построения каждого графика нам достаточно выбрать одну точку, так как вторая уже известна – это точка (0; 0).
Итак, для первого графика возьмем точку (1; 1)
Для второго графика возьмем точку (1; 2)
Для третьего графика (1; -1)
Для четвертого (1; -2)
По графику очень хорошо видно, что прямая пошла круче, чем прямая , угол прямой менее острый, при одинаковых значениях аргумента значение функции больше чем , но в обоих случаях угол острый и функция возрастает.
Обе прямые и имеют тупой угол наклона, обе функции убывают, но у прямой менее тупой и эта функция убывает быстрее.
Пример 4 – определить соотношение между угловыми коэффициентами:
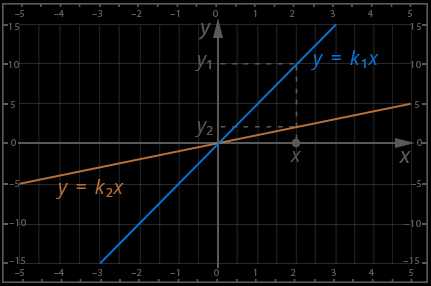
отсюда
Итак, роль углового коэффициента – это скорость роста функции.
Рассмотрим некоторые типовые задачи.
Пример 5:
Построить график прямой пропорциональности, если известно, что ему принадлежит точка с координатами (2; 8)
Для построения прямой нам нужно две точки, первая из них (0; 0), так как все графики прямой пропорциональности проходят через точку (0; 0), а вторая точка задана – это точка (2; 8).
Можно поступить иначе. Из заданной точки (2; 8) мы понимаем, что х=2 и у=8 удовлетворяет нашему уравнению вида , подставим эти значения и найдем k:
, отсюда . Итак, нам задано уравнение , которое мы легко можем построить.
Пример 6:
Построить график прямой пропорциональности и по нему ответить на множество вопросов.
Начнем с построения графика. Первая точка нам известна – для любого графика прямой пропорциональности это точка (0; 0). Для второй точки возьмем , тогда :
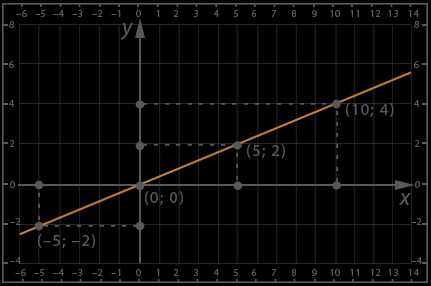
По графику требуется определить значение функции при следующих значениях аргумента: , , , ;
Кроме того, по заданному значению функции определить значение аргумента:
, ,
Определить по графику решение неравенств:
и
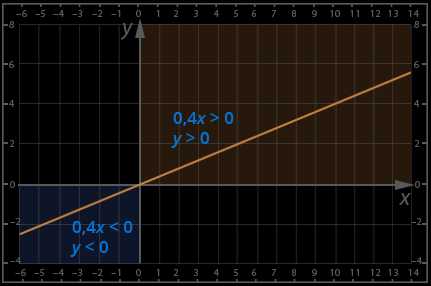
y<0 при x<0
y>0 при x>0
Пример 7 – найти наибольшее и наименьшее значение функции, если они существуют:
1)Задана функция , причем
2),
Построим график функции :

Для первого случая х меняется в пределах , значит, у меняется в пределах , значит на этом интервале минимум функции равен нулю, а максимум трем.
Для второго случая х меняется в пределах , значит, функция меняется в пределах , значит, минимальное значение функции на этом интервале есть и оно равно трем, а максимального значения функция не достигает.
Последний тип задач – по заданному графику определить угловой коэффициент.
Пример 8 – определить угловой коэффициент:
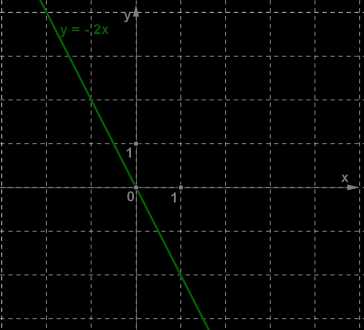
Задан график прямой пропорциональности.
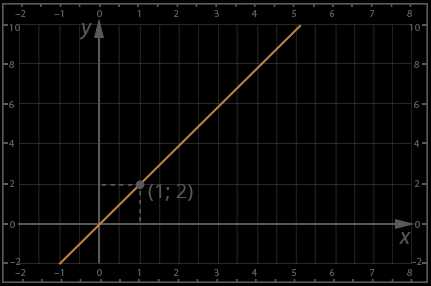
Мы видим, что график проходит через точку (1; 2), значит пара чисел х=1, у=2 удовлетворяет функции вида , значит, можем подставить значения в уравнение и найти k:
Итак, нам задан график функции
Вывод: в данном уроке мы рассмотрели частный случай линейной функции – прямую пропорциональность. Мы сформулировали свойства данной функции и основные типовые задачи, связанные с данной темой.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. ЕГЭ по математике (Источник).
2. Старая школа (Источник).
3. Портал Естественных Наук (Источник).
Рекомендованное домашнее задание
Задание 1: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 299, ст.68;
Задание 2: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 300, ст.68;
Задание 3: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 305, ст.68;
interneturok.ru
Линейная функция y = kx — урок. Алгебра, 7 класс.
Рассматривая линейную функцию вида \(y=kx + m\), особо выделяют случай, когда \(m=0\).
Тогда линейная функция принимает вид \(y=kx\).
Графиком линейной функции \(y=kx\) является прямая, проходящая через начало координат.
Важно уметь переходить от аналитической модели \(y=kx\) к геометрической и, наоборот, от геометрической к аналитической модели.
Например, рассмотрим прямую, изображённую на рисунке.
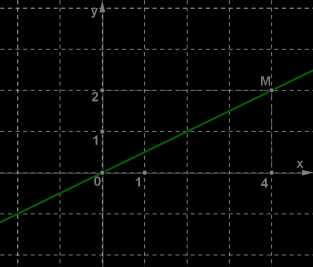
Эта прямая является графиком линейной функции \(y=kx\), так как проходит через начало координат. Нужно лишь определить значение коэффициента \(k\).
Из формулы линейной функции \(y=kx\) получим, что k=yx.
Поэтому для определения коэффициента \(k\) достаточно взять любую точку на прямой и найти отношение ординаты этой точки к её абсциссе.
Прямая проходит через точку \(M(4; 2)\), а для этой точки имеем 24=0,5. Значит, \(k=0,5\), и данная прямая является графиком линейной функции \(y=0,5x\).
График линейной функции \(y=kx\) обычно строят так: берут точку \((1; k)\) (если \(x = 1\), то из равенства \(y=kx\) выводим, что \(y=k\)) и проводят прямую через эту точку и начало координат.
Иногда вместо точки \((1; k)\) можно взять другую точку, более удобную.
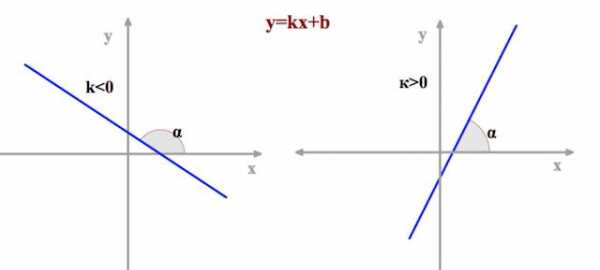
От коэффициента \(k\) зависит угол, который построенная прямая образует с положительным направлением оси \(x\).
Если \(k>0\), то этот угол острый (как на первом рисунке), а
если \(k<0\), то этот угол тупой (как на втором рисунке).
Поэтому коэффициент \(k\) в записи \(y=kx\) называют угловым коэффициентом.
Обобщая сведения о линейных функциях, можно сделать вывод:
прямая, служащая графиком линейной функции \(y=kx + m\), параллельна прямой, служащей графиком линейной функции \(y=kx\).
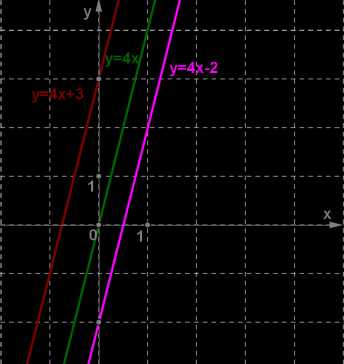
На рисунке показаны параллельные прямые с одним и тем же коэффициентом \(k = 4\).
Поэтому коэффициент \(k\) в записи \(y=kx + m\) также называют угловым коэффициентом, и
если \(k>0\), то прямая \(y=kx + m\) образует с положительным направлением оси \(x\) острый угол;
если \(k<0\), то этот угол тупой.
www.yaklass.ru
Элементарные функции. Линейная функция | Подготовка к ЕГЭ по математике
Категория: Справочные материалыФункции и графики
Линейная функция – функция вида , где и – некоторые числа.
Число называется угловым коэффициентом прямой (и равняется тангенсу угла наклона прямой к положительному направлению оси абсцисс). Число называется свободным членом. График линейной функции является прямой линией, откуда и вытекает название.
 Графики линейных функций, имеющие один и тот же угловой коэффициент, параллельны друг другу ( см. рис. слева (ниже)).
Графики линейных функций, имеющие один и тот же угловой коэффициент, параллельны друг другу ( см. рис. слева (ниже)).
Графики функций, коэффициенты и которых связаны следующим образом: , перпендикулярны друг другу (рис. справа).
 Частные случаи:
Частные случаи:
1)
Тогда , графиком является прямая, параллельная оси абсцисс, проходящая, в частности, через точку (рис. слева (ниже))
2)
Тогда (прямая пропорциональность), графиком является прямая, проходящая через начало координат (рис. справа).
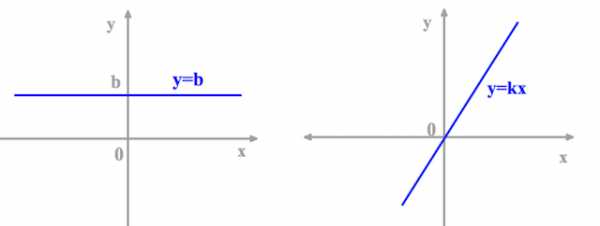
Строить график линейной функции можно двумя основными способами:
1) Через две точки
Одну из точек обычно берут . Эта точка сразу же видна, ведь свободный член в формуле задает ординату точки пересечения с осью (оy). Вторую точку выбираем любую (), лишь бы удобно было в ней считать соответствующее значение .
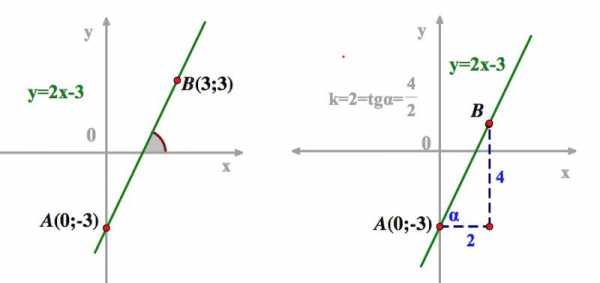
2) По угловому коэффициенту
Строим на координатной плоскости произвольную точку прямой. Проводим через эту точку прямую, образующую с осью (OX) угол, тангенс которого равен k
egemaximum.ru
