Функция прямой
Линейная функция – это функция вида
f(x)=k∙x+b
или
y(x)=k∙x+b,
где
x-аргумент (независимая переменная),
y- функция (зависимая переменная),
k и b- некоторые постоянные числа
k=const
b=const
Графиком линейной функции является прямая.
Для построения графика достаточно двух точек, т.к. через две точки можно провести прямую и притом только одну.
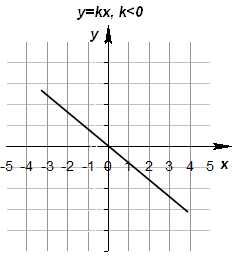
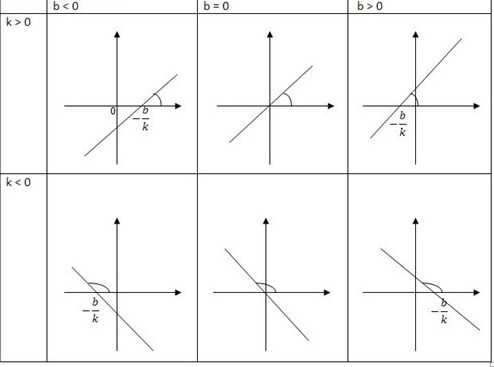
Если k˃0, то график расположен в 1-й и 3-й координатных четвертях. Если k˂0, то график расположен в 2-й и 4-й координатных четвертях.
Число k называют угловым коэффициентом прямой графика функции y(x)=kx+b. Если k˃0, то угол наклона прямой y(x)= kx+b к положительному направлению Ох — острый; если k˂0, то этот угол- тупой.
Коэффициент b показывает точку пересечения графика с осью ОУ (0; b).
a) k≠0; b=0,
тогда
y(x)=k∙x+0,
или
y(x)=k∙x
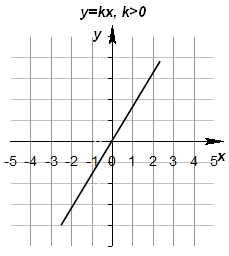
y(x)=k∙x— частный случай типичной функции носит название прямая пропорциональность. Графиком является прямая, проходящая через начало координат, поэтому для построения этого графика достаточно одной точки.
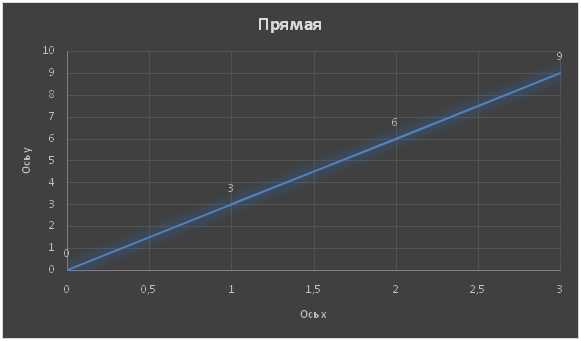
График линейной функции
y=kx
Где коэффициент k = 3, следовательно
y=3x
График функции будет возрастать и иметь острый угол с осью Ох т.к. коэффициент k имеет знак плюс.
ООФ линейной функции
X∈R
D(f)=R
ОЗФ линейной функции
Y∈R
E(f)=R
Кроме случая, где
Y(x)=b
Так же линейная функция вида
y=kx+b
Является функцией общего вида.
Б) Если k=0; b≠0,
тогда
y(x)=0∙x+b,
или
y(x)=b
В этом случае графиком является прямая параллельная оси Ох и проходящая через точку (0;b).
В) Если k≠0; b≠0, то линейная функция имеет вид y(x)=k∙x+b.
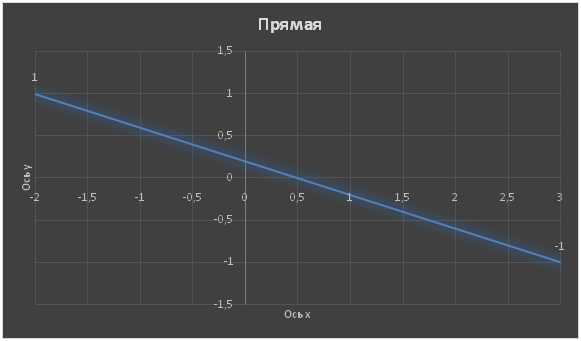
Пример 1. Построить график функции y(x)= -2x+5
Пример 2. Найдём нули функции у=3х+1, у=0;
3х+1=0;
– нули функции.
Ответ: или (;0)
Пример 3. Определить значение функции y=-x+3 для x=1 и x=-1
Решение:
y(1)=-1+3=2
y(-1)=-(-1)+3=1+3=4
Ответ: y_1=2; y_2=4.
Пример 4. Определить координаты их точки пересечения или доказать, что графики не пересекаются. Пусть даны функции y1=10∙x-8 и y2=-3∙x+5.
Если графики функций пересекаются, то значение функций в этой точке равны
x1=x2
y1=y2
т.е.
10х-8=-3х+5;
13х=13;
x=1
Подставим х=1, то y1 (1)=10∙1-8=2.
Замечание. Подставить полученное значение аргумента можно и в функцию y 2=-3∙x+5, тогда получим тот же самый ответ y2 (1)=-3∙1+5=2.
y=2- ордината точки пересечения.
(1;2)- точка пересечения графиков функций у=10х-8 и у=-3х+5.
Ответ: (1;2)
Пример 5.
Построить графики функций y1(x)= x+3 и y2(x)= x-1.
Решение:
Можно заметить, что коэффициент k=1 для обеих функций.
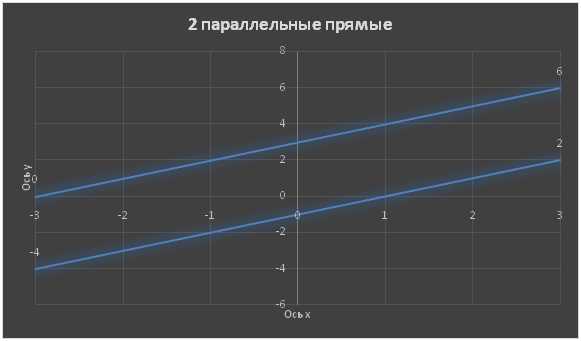
Из выше сказанного следует, что если коэффициенты линейной функции равны, то их графики в системе координат расположены параллельно.
Пример 6.
Построим два графика функции.
Первый график имеет формулу
y1= -2x+4
Второй график имеет формулу
у2=0,5х+4
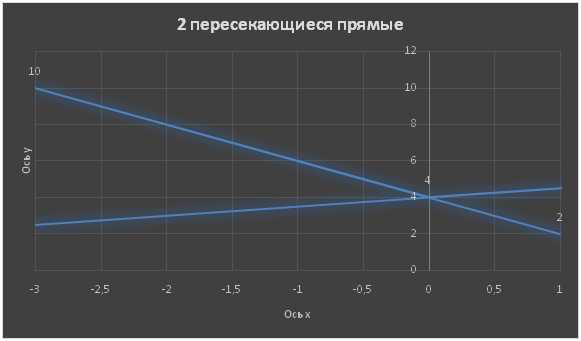
В данном случае перед нами график двух прямых, пересекающихся в точке (0;4). Это значит, что коэффициент b, отвечающий за высоту подъёма графика над осью Ох, если х=0. Значит мы может полагать, что коэффициент bу обоих графиков равен 4.
Автор статьи: Глотов Василий Максимович
Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна
www.teslalab.ru
Линейная функция, график — прямая. Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
Тестирование онлайн
Линейная функция
Определение. График
Линейной функцией называется функция вида
где k, b — некоторые числа.
Функция вида называется прямой пропорциональностью, является частным случаем линейной зависимости.
Графиком линейной функции является прямая линия.
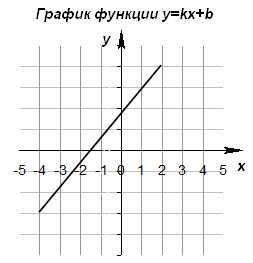
Для построения графика достаточно знать координаты двух точек.
Свойства линейной функции
1) Область определения функции — множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке , а ось Оу — в точке (0; b).
7) — является нулем функции.
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k.
9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
При k: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k — тупой, если k=0, то прямая совпадает с осью Ох.
Для построения графика функции — прямой линии, очевидно, достаточно двух точек.
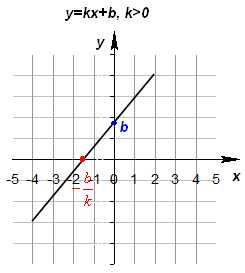

Особые случаи
1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.
2) Если k=0, получим уравнение y=b. Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).

fizmat.by
Линейная функция, ее свойства и график
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k>0, то график наклонен вправо. Причем, чем больше значение k, тем круче идет прямая.
если kКоэффициент b отвечает за сдвиг графика вдоль оси OY:
если b>0, то график функции y = kx + b получается из графика функции y = kx сдвигом на b единиц вверх вдоль оси OY
если b
Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) ky = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b
Подведем итоги в виде таблицы:
spishy-u-antoshki.ru
Линейная функция ее свойства и график. Угловой коэффициент линейной функции
Линейная функция
Линейная функция
Линейная функция – это функция вида:
y = kx + b
здесь k и b являются действительными числами.
Свойства линейной функции
Линейная функция имеет следующие свойства:
1. y = kx + b – это ни чётная, ни нечётная функция;
2. Область определения функции y = kx + b – вся числовая прямая;
3. Множество значений линейной функции – вся числовая прямая;
4. Если k больше 0, то функция возрастает, а если k меньше 0, то линейная функция убывает.
Угловой коэффициент линейной функции
Коэффициент k в формуле линейной функции называется угловым коэффициентом.
Угловой коэффициент определяет угол между графиком линейной функции и положительным направлением оси абсцисс.
График линейной функции
График линейной функции есть прямая. Вот график линейной функции y = 2x + 1
здесь угловой коэффициент больше нуля, угол прямой линии y = 2x + 1 с положительным направлением оси x – острый.
А теперь посмотрим как изменится график линейной функции y = 2x + 1, если угловой коэффициент сделать отрицательным, т.е. y = -2x + 1
здесь угол прямой линии y = -2x + 1 с положительным направлением оси x – тупой.
Как изменяется график линейной функции в зависимости от числа b в формуле линейной функции y = kx + b? Если b увеличивать, график смещается вверх, если число b уменьшать, то график y = kx + b смещается вниз.
График линейной функции y = kx + b построить вы можете сами прямо сейчас с помощью построителя графиков. Выберете в нём вид функции «Линейная: y = k * x + b» и нажмите кнопку «Построить график». Проведите эксперименты: устанавливайте угловые коэффициенты больше и меньше нуля, меняйте значения числа b и посмотрите, как будет изменяться график линейной функции.
www.sbp-program.ru
Линейная функция | Алгебра
Определение.
Линейная функция — это функция вида y=kx+b, где k и b — числа.
Графиком линейной функции является прямая.
Для построения прямой достаточно взять две точки.
Если x=0, то y=b.
Если y=0, x= -b/x.
Таким образом, график линейной функции проходит через точки (0;b) и (-b/k;0).
Свойства линейной функции
1) Область определения линейной функции состоит из всех чисел:
D: x∈(-∞;∞).
2) Область значений линейной функции состоит из всех чисел:
E: y∈(-∞;∞).
3) Нуль функции (y=0) x= -b/x.
4) При k>0 линейная функция возрастает.
При k<0 — убывает.
5) При k>0
Функция принимает положительные значения при x> -b/k, или
Функция принимает отрицательные значения при x< -b/k, или
При k<0
Функция принимает положительные значения при x< -b/k, или
Функция принимает отрицательные значения при x> -b/k, или
Число k называется угловым коэффициентом прямой. По значению k можно определить угол α, который прямая y=kx+b образует с положительным направлением оси Ox.
При k>0 угол α острый, при k<0 угол α — тупой.
Если k=0, линейная функции принимает вид y=b. График этой функции — прямая, параллельная оси Ox.
Например, на рисунке изображены графики линейных функций y=2 и y= -4.
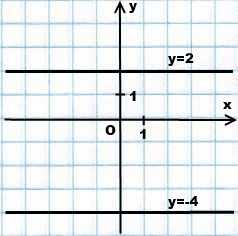
Функция в этом случае постоянная (ни возрастает, ни убывает).
www.algebraclass.ru
С3 ГИА — построение графиков функций.
Для того, чтобы хорошо решать это задание, нужно быть знакомым с построением различных графиков функций, в том числе содержащих модуль. Предлагаю тем, кто неуверенно себя чувствует при решении таких заданий, перейти по ссылкам и изучить (или повторить) данные разделы. Задание С3 связано как с исследованием расположения корней квадратного трехчлена, так и с определением области определения функции, и области ее значений. На конкретных примерах мы попробуем научиться решать различные типы таких заданий.
Задача 1. Построить график функции и определить, при каких значениях график функции имеет с графиком 1 общую точку. Построить все такие прямые.
Задача о касательных к параболе
Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график – это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент ). Такая прямая только в одном случае имеет с параболой одну общую точку – если является касательной. Причем, поскольку данная парабола симметрична относительно оси ординат, то к ней можно провести две касательных – с точками касания в первом и третьем квадрантах: Чтобы определить, в какой точке прямая коснется параболы, нужно приравнять обе функции:
Поскольку точка касания – единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: Откуда и . Абсциссу точки касания можно найти, если приравнять два уравнения, подставив найденный коэффициент в уравнение прямой: и решить это уравнение: Тогда касание произойдет в точке и симметричной ей точке .
Задача 2. Построить график функции и определить, при каких значениях график функции имеет с графиком три или более общие точки.
График, который подвергнется преобразованиям
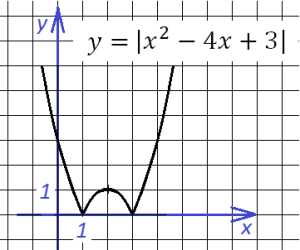
Преобразованный график
Строить этот график будем поэтапно: сначала построим график , затем – график функции , и, наконец, искомый – : Парабола с ветвями, направленными вверх, стандартной формы, координаты вершины (2;-1) Теперь построим график . Поскольку модуль берется от всего выражения, то, чтобы получить этот график, нужно отразить вверх симметрично относительно оси х все точки, имеющие отрицательную ординату. И, наконец, поставив минус, мы “перевернем” весь график вверх тормашками:
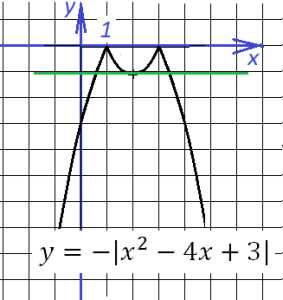
“Опрокидываем” преобразованный график
Осталось выяснить, в каком же случае прямая – а это прямая, параллельная оси абсцисс – будет иметь три (или же более) общие точки с графиком построенной нами функции. Прямая показана на рисунке зеленым цветом. Видно, что ниже указанного положения прямая будет иметь только две общие точки с графиком. Если , то прямая имеет три точки с графиком – пересекает две его ветви и касается вершины. Выше прямая будет иметь четыре точки пересечения с графиком, однако при точек пересечения уже снова две. Значит, ответ надо записать так: [-1;0)
Задача 3. Построить график функции и определить, при каких значениях график функции имеет с ним три и более общие точки.
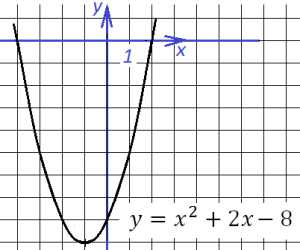
Исходный график
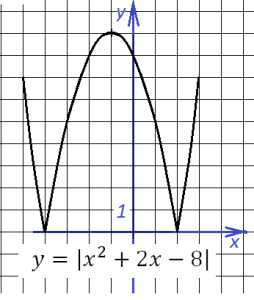
Окончательный вид
Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно – четыре) общих точки графики и будут иметь при (0;9]
Задача 4. Построить график функции и определить, при каких значениях график функции имеет с ним 2 общие точки.
Из условия ясно, что такой график состоит из двух кусочков. Один из них – прямая, второй – парабола. Первый существует в точке 1 и левее ее, второй – правее этой точки. Нарисуем эти графики:
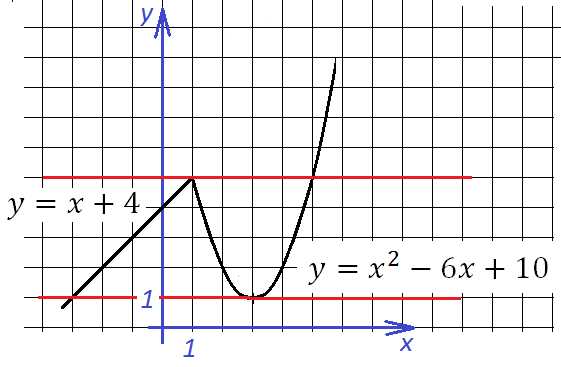
Кусочная функция
Координаты вершины параболы: ;
Красным показаны прямые и – именно они, и только они, имеют две общие точки с построенным графиком. Ответ: , .
Задача 5. Построить график функции и определить, при каких значениях график функции не имеет с графиком общих точек.
Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: . Теперь попробуем упростить данное выражение:
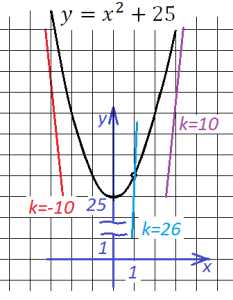
Определение коэффициента наклона касательной
Полученная функция – квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) – выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат – а именно таким будет график функции , не будет иметь с параболой общих точек в трех случаях: если коэффициент меньше, чем у касательной, расположенной справа, или он больше, чем у касательной, расположенной слева, или искомая прямая проходит прямо через выколотую точку. Наверное, проще найти каков этот коэффициент именно в третьем случае: так как прямая проходит через начало координат, достаточно подставить координаты нашей выколотой точки в уравнение прямой и найти : , откуда . Проверим, не будет ли такая прямая иметь общих точек с параболой. Приравняем . По сумме коэффициентов это уравнение имеет корень 1, но и второй корень – 25, поэтому такая прямая будет иметь еще одну точку пересечения с параболой. В ответ эту прямую мы не включим. Теперь определим коэффициент наклона касательных, для этого приравняем оба уравнения: , и найдем дискриминант, который должен быть равен нулю при наличии единственной общей точки у двух этих графиков функций: Откуда и Абсциссу точки касания можно найти, если приравнять два уравнения, подставив найденный коэффициент в уравнение прямой: и решить это уравнение: Тогда касание произойдет в точке и симметричной ей точке . Ответ: , .
Задача 6. Построить график функции и определить, при каких значениях он не имеет общих точек с графиком функции .
Гипербола с выколотой точкой
Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – видим, что графиком будет обычная гипербола, однако точка – выколотая точка. В точке гипербола не существует, оси координат – ее асимптоты (одна из них войдет в ответ). Тогда, если прямая пройдет через выколотую точку, графики не будут иметь общих точек. Найдем : для этого определим ординату выколотой точки: : Ответ: и .
Задача 7. Построить график функции и определить, при каких значениях график функции имеет с графиком 1 общую точку.
Подбор коэффициента наклона прямой
Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – видим, что графиком будет обычная гипербола, однако точка – выколота. В точке гипербола не существует, оси координат – ее асимптоты. Тогда, если прямая пройдет через выколотую точку, графики будут иметь одну общую точку. Найдем : для этого подставим в уравнение прямой абсциссу и ординату выколотой точки: , : Ответ:
Задача 8. Построить график функции и определить, при каких значениях график функции имеет с ним 2 общие точки.
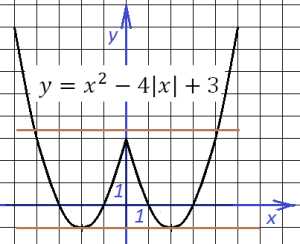
Построение функции с модулем
Эта функция – функция типа , и чтобы построить график данной функции, необходимо отразить всю часть графика, расположенную справа от оси х, налево: Тогда, если , то график коснется обеих вершинок нашей “дублированной” параболы, то есть – один из ответов. Также, если пересечет обе ветви параболы, то есть все нас устраивают. Ответ: ,.
Задача 9. Построить график функции и определить, при каких значениях график функции не имеет с ним общих точек.
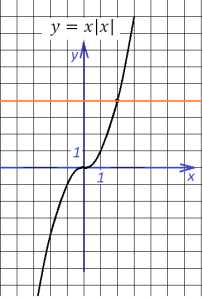
Кубическая парабола с выколотой точкой
Определим ОДЗ исходной функции: . Теперь можно упростить выражение: .
График представлен на рисунке. Не забудем про выколотую точку – это точка с координатами (2;4). Поэтому, если прямая пройдет именно через эту точку, она не будет иметь общих точек с полученным нами графиком. Ответ: с=4.
Задача 10. Построить график функции и определить, при каких значениях график функции имеет с ним одну общую точку.
Для того, чтобы построить данный график, необходимо раскрыть модули. С этой целью приравняем подмодульное выражение к нулю, чтобы узнать, в какой точке оно меняет знак: и Нанесем эти точки на числовую прямую и расставим знаки:
У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 2. 3. Тогда наша функция – кусочно-линейная: .
Она выглядит так:
Кусочно-линейная функция
Зеленым цветом показано одно из возможных положений прямой . При таком расположении прямой , и может расти бесконечно. Заметим, что крайнее положение прямой – при k=1. При таком коэффициенте наклона она параллельна правой и левой частям графика, и имеет с ним одну точку пересечения – точку (0;0). Точно так же коэффициент наклона может быть и отрицательным. При этом коэффициент k=-1 – не войдет в ответ, так как в этом случае функция будет иметь общий отрезок с кусочно-линейной функцией, что не соответствует требованиям задачи. Таким образом,
Ответ: ).
Задача 11. При каких вершины парабол и расположены по одну сторону от оси х?
Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй – положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая – нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого – отрицателен. Это приводит нас к двум системам неравенств:

Дискриминант и наличие пересечений параболы с осью х
.
Или же наоборот: . Эти два случая изображены на рисунке:
Определим дискриминанты обоих квадратных уравнений:
Тогда имеем систему неравенств:
– решений нет, так как квадрат числа – неотрицателен, и сумма квадрата числа с положительным числом не может быть меньше ноля.
– в этой системе второе неравенство всегда соблюдается, решение первого – , ,
Мы рассмотрели один способ решения – с использованием дискриминанта. Есть еще один способ решения такого задания – с помощью координат вершины параболы. Решим последнюю задачу вторым способом.
Нам потребуется определить координаты вершин обеих парабол:
1.
2.
Ординаты вершин должны иметь один знак по условию, тогда имеем систему неравенств:
– вторая система решений не имеет, а именно, нет решений у второго неравенства, поэтому решим первую. Второе неравенство первой системы справедливо всегда, осталось решить неравенство:
Решение этого неравенства и есть ответ задачи:
До встречи в новых постах, удачи на экзаменах!
easy-physic.ru
