Радианная мера угла и градусная – . . .

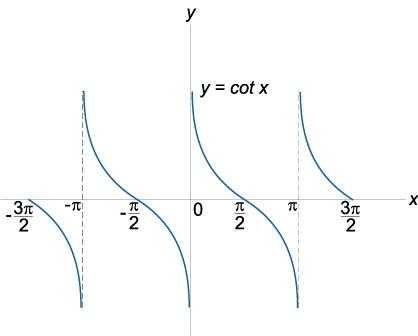
«Градусная и радианная мера угла»

Учитель математики КГУ СОШ №17 Тельгузинова Р.Ш.

Алгебра – 9 класс Дата_______________

Тема: «Градусная и радианная мера угла»  

Цель урока

1. Рассмотреть связь между радианной и градусной мерами угла;

2. Закрепить умения выполнять переход от радианной меры угла к градусной мере и наоборот.

Тип урока изучение новой темы

Орг. момент приветствие, проверка готовности и посещаемости

Проверка Д/З

Повторение Вспомним из курса геометрии, как определяется угол

Это часть плоскости, заключённая между двумя полупрямыми

Перечислить все виды углов, которые вы знаете, поможет следующее задание:

Соотнесите номер каждого угла его названию.

Изучение нового материала

Возьмем на координатной плоскости окружность с центром в точке О и радиусом R. Отметим на ней дугу РМ, длина которой равна R и угол РОМ.

Центральный угол, опирающийся на дугу, длина которой равна радиусу

окружности, называется углом в 1 радиан.

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

И наоборот

Так как π = 3,14, то 1 рад = 57,3°

Посмотрите на чертёж и прикиньте, сколько радиан включает в себя развёрнутый угол (3) Если быть точнее, то 3,14.

Что это за число? Верно, это число  Запишем сделанный вывод: (щелчок мыши)180°=  рад (1)

А сколько радиан содержит прямой угол? А полный? Запишем (щелчок мыши)

180°<— развёрнутый угол—> 

90°<— прямой угол—>

360°<—полный угол—> 2

Если угол содержит a радиан, то его градусная мера равна

И наоборот

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

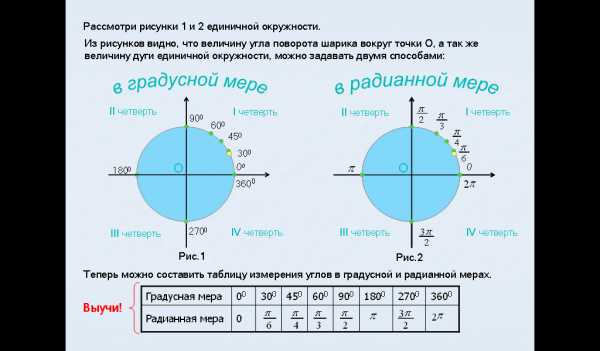
В таблице указаны наиболее часто встречающиеся 

углы в градусной и радианной мере.

Пример 1.

Найти радианную меру угла равного а) 40° ,  б)120° ,  в)105°

Решение

а) 40° = 40·π / 180 = 2π/9

б) 120° = 120·π/180 = 2π/3

в) 105° = 105·π/180 = 7π/12

Пример 2.

Найти градусную меру угла выраженного в радианах а) π/6 ,  б) π/9,  в) 2·π/3

Решение

а) π/6 = 180°/6 = 30°

б) π/9 = 180°/9 = 20°

в) 2π/3 = 2·180°/6 = 120°

Закрепление

1. Заполнить таблицу.

Определить градусные и радианные интервалы всех четвертей.

Ответы проверяем

2. Определить, в какой четверти находятся углы.

= 25°, = – 100°, 

 = 220°,  = 460°

Постановка Д/З 264 , 265 (в,г)

Рефлексия

infourok.ru

Радианная и градусная мера угла

5 мая 2014

Сегодняшний видеоурок — один из ключевых в курсе тригонометрии. Мы расширим классическое определение синуса, косинуса и тангенса на произвольные углы (в т.ч. отрицательные), а введем новое определение — радианную меру угла.

Сегодня мы поговорим о такой теме, которая волнует всех учеников 8-9 классов, когда они начинают изучать серьезную взрослую тригонометрию. Речь идет о радианной мере угла, а также о переводе из радианной в градусную меру угла и обратно. Но, прежде чем мы начнем решать какие-то задачи на вычисления радианной меры, мне хотелось бы вспомнить старое определение, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Немного теории

Давайте нарисуем прямоугольный треугольник, назовем его

, причем CC будет прямым:

Угол AA будет равен α\alpha градусов. В этом случае, как вы помните из школьного курса геометрии, синус, косинус и тангенс будут одинаковые:

sinα=BCAB

\sin \alpha =\frac{BC}{AB}

cosα=ACAB

\cos \alpha =\frac{AC}{AB}

tgα=BCAC

tg\alpha =\frac{BC}{AC}

Как видите, классическое определение синуса, косинуса, тангенса и котангенса завязано на прямоугольном треугольнике, и α\alpha в любом случае должен быть больше 0º и меньше 90º.

Несмотря на это, возникла необходимость расширить определение тригонометрических функций за пределы этого интервала от 0º до 90º. Как это происходит, и какие возникают при этом эффекты — вот сейчас об этом и поговорим.

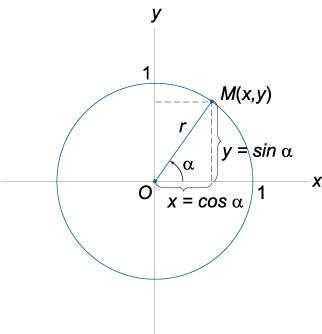
Для начала давайте рассмотрим координатную плоскость: проведем оси xx, yy, а также построим единичную окружность с центром в начале координат:

 

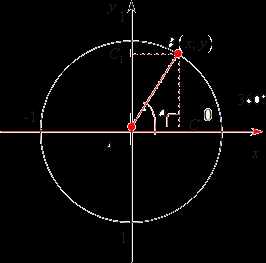
Небольшое уточнение в терминологии, что значит единичная окружность? Все очень просто. Это означает, что ее радиус равен строго 1. Другими словами, она проходит через точку (1; 0), а также (0; 1). И через две остальные точки эта окружность также проходит. Теперь нам нужно пустить от начала координат луч вдоль оси OxOx. Речь идет о положительном направлении оси OxOx. Затем мы отметим α\alpha в направлении xx к yy. Разумеется, этот луч пересечет наш круг в неком значении, давайте обозначим его точкой BB. А начало координат обозначим точкой AA. Проведем из BB высоту к оси абсцисс xx. Мы получим CC. Вот мы снова получили тот же самый прямоугольный треугольник ABCABC с углом α\alpha , вершина которого совпадает с началом координат.

Что такое синус?

Теперь давайте перепишем синус, косинус и тангенс с учетом всех изменений для красного треугольника. Запишем:

sinα=BCAB

\sin \alpha =\frac{BC}{AB}

Все то же самое. Однако заметим, что BB лежит уже не в каком-то неопределенном пространстве, она имеет какие-то координаты, поскольку лежит в плоскости OxyOxy. Пусть ее координаты будут (x;y)\left( x;y \right). Мы не знаем точно, чему они равны, потому что не знаем угол α\alpha . В таком случае длина отрезка BCBCравняется yy, т. е. ординате точки BB. Вместо BCBC мы можем записать yy, а вместо ABAB — 1. ABAB — это тот же самый радиус нашего круга, а радиус — 1. Записываем:

sinα=BCAB=yr=y

\sin \alpha =\frac{BC}{AB}=\frac{y}{r}=y

Таким образом, мы можем записать, что sinα\sin \alpha на самом деле равен ординате конца подвижного радиуса. Вот именно эту фразу чаще всего встречают ученики в школьных учебниках по математике. Поэтому, прежде чем двинемся дальше, давайте еще раз внимательно посмотрим на треугольник ABCABC и, в частности, на BB.

Мы провели еще одну высоту, назовем ее BC1B{{C}_{1}}. Что можно сказать про C1{{C}_{1}}, точнее, про отрезок AC1A{{C}_{1}} — это координата у BB. С другой стороны, отрезок ACAC, т. е. расстояние от AA до CC — это координата xx точки CC и, соответственно, xx точки BB. Нам несложно будет доказать, что отрезки BCBC и AC1A{{C}_{1}} равны. Тогда мы можем утверждать, что и отрезок ABAB тоже равен yy. Таким образом, с синусом мы разобрались. Действительно, синус угла α\alpha равен ординате конца подвижного радиуса, проведенного в точку BB. Теперь давайте запишем те же самые выражения для косинуса и тангенса.

Что такое косинус? 

Это отношение прилежащего катета (в нашем случае это катет ACAC) к гипотенузе (у нас ABAB). Но что такое ACAC? Только что мы убедились, что ACAC — это абсцисса, т. е. координата xx. А ABAB — это тот же самый радиус, т. е. 1. Запишем:

cosα=ACAB=xr=x

\cos \alpha =\frac{AC}{AB}=\frac{x}{r}=x

Что такое тангенс?

Теперь разбираемся с tgαtg\alpha . Тут все еще проще. Что такое тангенс? Это отношение противолежащего катета (а нашем случае это BCBC) к прилежащему катету (в нашем случае это ACAC). Запишем:

tgα=BCAC=yx

tg\alpha =\frac{BC}{AC}=\frac{y}{x}

Таким образом, tgtg — это отношение ординаты к абсциссе конца подвижного радиуса.

И в этот момент многие ученики наверняка спросят: «А зачем вообще вся эта сложность?». В данном случае когда BB просто задается пересечением луча с окружностью, мы можем отложить любой угол α\alpha . Теперь никаких ограничений на обозначение α\alpha не накладывается. Он не обязан быть углом пределах от 0º до 90º.

Вычисление радианной меры угла

Теперь, когда мы разобрались с основными определениями тригонометрических функций, перейдем непосредственно к сегодняшней теме урока.

Для начала давайте рассмотрим угол в 180º. Тогда наш луч поддет в противоположном направлении. Точка В в нашем треугольнике высекает определенную дугу окружности. Назовем ее дуга BCBC. Ее легко посчитать по формуле длины окружности:

l=2πr

l=2\pi r

π ˜3,14

\pi \tilde{\ }3,14. Но сейчас нас это не интересует. Поскольку наша окружность всегда имеет фиксированный радиус 1, то длина будет равна:

l=2π

l=2\pi

Однако 2π2\pi — это вся окружность, т. е. полный оборот. А мы если отступим на 180º, то получим только ее половину. Следовательно, дуга окружности будет равна:

l(180o)=2π2=π

l\left( 180{}^\text{o} \right)=\frac{2\pi }{2}=\pi

И вот тут возникает замечательный эффект. Дело в том, что один и тот же угол α\alpha мы можем обозначать как за 180º, т. е. использовать стандартную меру угла (а не радианную), так и длинной вот этой дуги, т. е. мы можем поставить углу α\alpha соответствующее число π\pi . Так вот это число π\pi , т. е. другими словами, угол, измеренный не в градусах, а в длине дуги, которую этот угол высекает. Называется это радианная мера угла и обозначается π\pi — радиан.

Сегодня же для того чтобы начать решать задачи на радианную меру и считать значение тригонометрических функций, просто запомните, что π\pi рад = 180º. Другими словами, если вам непривычно работать с радианными значениями, то везде, где вы видите в синусах, косинусах и тангенсах конструкцию π\pi , вы можете смело заменить это π на 180º и перейти к знакомой градусной от радианной меры. Давайте попробуем и сосчитаем первое выражение и найдем радианную меру:

sin π 4cos π 6tg π 3=2√2⋅3√2⋅3√=32√4\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6}tg\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}\cdot \sqrt{3}=\frac{3\sqrt{2}}{4}

Давайте выпишем отдельно каждую из этих функций:

sin π 4=sin180∘4=sin45∘=2√2\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\sin \frac{180{}^\circ }{4}=\sin 45{}^\circ =\frac{\sqrt{2}}{2}

cos π 6=cos180∘6=cos30∘=3√2\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\cos \frac{180{}^\circ }{6}=\cos 30{}^\circ =\frac{\sqrt{3}}{2}

tg π 3=tg180∘3=tg60∘=3√tg\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=tg\frac{180{}^\circ }{3}=tg60{}^\circ =\sqrt{3}

Теперь записываем все три множителя в единую конструкцию для нахождения радианного значения. Вот и все, мы получили ответ.

Переходим ко второму выражению и найдем радианную меру:

cos π 3sin π 4ctg π 6=12⋅2√2⋅3√=6√4\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}ctg\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{1}{2}\cdot \frac{\sqrt{2}}{2}\cdot \sqrt{3}=\frac{\sqrt{6}}{4}

Опять записываем каждую функцию отдельно:

cos π 3=cos60∘=12\cos \frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\cos 60{}^\circ =\frac{1}{2}

sin π 4=sin45∘=2√2\sin \frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\sin 45{}^\circ =\frac{\sqrt{2}}{2}

ctgπ6=ctg30∘=3√ctg\frac{\pi }{6}=ctg30{}^\circ =\sqrt{3}

Опять собираем все полученные числа.

Как видите, ничего сложно в радианных мерах угла нет. Если эта тема покажется вам слишком сложной, просто запомните, что π\pi рад = 180º, и везде, где вы видите π\pi , можете смело писать 180º.

Еще одним важным следствием нового определения тригонометрического круга является то, что синус, косинус и тангенс могут быть отрицательными. Если раньше все сводилось к длинам катетов и гипотенузы, то теперь перед нами абсциссы и ординаты некой точки. При этом помните, что откладывание угла всегда идет в направлении от оси OxOx к оси OyOy, причем идет речь именно о положительных направлениях этих осей.

Чтобы понять и навсегда запомнить, где находится положительное направление оси, просто помните правило: туда, куда указывает стрелка при х и при у, это и есть то самое положительное направление оси.

Вот это и все, о чем я хотел рассказать в сегодняшнем видеоуроке о радианных мерах. Если вы что-то не поняли, или если этот материал показался вам слишком сложным, то пересмотрите его еще раз, попробуйте выполнить всю последовательность вычислений на нахождения радианных значений, которую мы сегодня выполнили на уроке.  

Смотрите также:

1. Как быстро запомнить таблицу синусов и косинусов
2. Значение тригонометрических функций
3. Пробный ЕГЭ 2012 от 7 декабря. Вариант 1 (без логарифмов)
4. Тест к уроку «Что такое числовая дробь» (легкий)
5. Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
6. ЕГЭ-2014 по математике и открытый банк задач

www.berdov.com

Радианная мера угла

Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что градусом называют величину центрального угла, которому соответствует  часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.

А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.

Давайте изобразим окружность с центром в точке  и радиусом . Затем проведём вертикальную прямую, которая касается окружности в точке . Эту прямую мы будем считать числовой осью с началом отсчёта в точке . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.

Отметим на прямой несколько точек:  и ,  и ,  и ,  и ,  и .

Теперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами , , ,  перейдут соответственно в точки окружности , , , . При этом длина дуги  равна , длина дуги  равна , длина дуги  равна , длина дуги  равна .

Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.

Так, точке прямой с координатой  ставится в соответствие точка . А значит, угол  можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол  следует считать равным , а угол  равным .

А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.

Единичный угол  называют углом в один радиан. Записывают так:  рад.

И напомним, что длина дуги  равна радиусу нашей окружности.

Сейчас давайте рассмотрим окружность радиуса . И отметим на ней дугу , равную длине радиуса окружности, и угол .

И такой угол называется углом в один радиан? Верно.

Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной , то есть полуокружности, соответствует центральный угол, равный . Следовательно, дуге окружности длиной  соответствует угол в  раз меньший.

Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что рад . , тогда рад .

Если угол содержит  рад, то рад . Эту формулу называют формулой перехода от радианной меры к градусной.

Давайте с вами найдём градусную меру угла, равного  рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим  вместо : . Сократим на  и на . И в результате получим .

Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в  равен  рад, то  рад. Тогда  рад. Такую формулу называют формулой перехода от градусной меры к радианной.

Найдём радианную меру угла, равного . Воспользуемся формулой перехода от градусной меры к радианной. Подставим  вместо : . Сократим  и  на . И в результате получим .

Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: . При этом обозначение градуса в записи меры угла пропускать нельзя.

В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.

Отметим, что радианная мера углов позволяет значительно упростить многие формулы в математике, физике, механике. В частности, радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в  рад стягивает дугу, длина которой равна радиусу , а значит, угол в  рад стягивает дугу длиной: . Если , то эта формула принимает совсем простой вид: , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.

Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса , образованного углом в  рад, равна , где .

Докажем это. Известно, что площадь круга вычисляется по формуле: . Площадь полукруга, то есть кругового сектора в  рад: . Тогда площадь сектора в  рад в  раз меньше, то есть . Следовательно, площадь сектора в  рад равна .

Ну а сейчас давайте выполним несколько заданий.

Первое задание. Найдите градусную меру угла, выраженную в радианах: а) ; б) ; в) ; г) ; д) .

Решение.

Второе задание. Найдите радианную меру угла, выраженного в градусах: а) ; б) ; в) ; г) .

Решение.

Следующее задание. Чему равен радиус окружности, если дуге длиной  см соответствует центральный угол в  рад?

Решение.

И ещё одно задание. Дуге кругового сектора соответствует угол, равный  рад. Чему равна площадь сектора, если радиус круга равен  см?

Решение.

Ну а сейчас немного истории.

Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.

В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).

videouroki.net

Математика. Градусная и радианная мера угла.

Градусная мера угла.

Градусы придумали в Древнем Вавилоне. Давненько это было… Веков 40 назад… И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?

Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно… Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя… В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926… раз.

Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.

Для практического применения принято запоминать всего две цифры после запятой. Запоминаем: 

Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:

 Где L — длина окружности, а d — её диаметр.

В геометрии пригодится.

Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена. И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245… И что мне делать? Нет уж…» Пришлось послушаться. Природу не обманешь…

Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь — радиан!

Радианная мера угла.

 

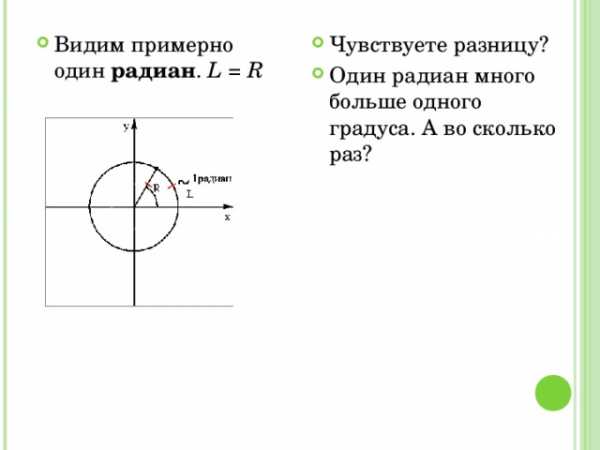
Что такое радиан? В основе определения радиана — всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса (R). Смотрим картинки.

Будем считать, что этот малюсенький угол имеет величину 1 

градус:

 

Маленький такой угол, почти и нет его… Наводим курсор на картинку (или коснёмся картинки на планшете) и видим примерно один радиан. L = R

Чувствуете разницу?

 

Один радиан много больше одного градуса. А во сколько раз?

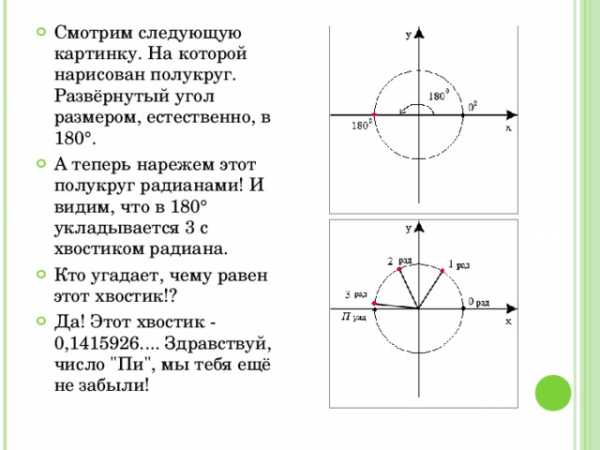
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.

 

А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.

Кто угадает, чему равен этот хвостик!?

Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!

Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто: 

Вот теперь совершенно осмысленно можно записать приближённое равенство: 

Или точное равенство: 

Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:

Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.

Но главное умение этой темы — перевод градусов в радианы и обратно.

Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан? Вот и пишем:

Или, более экзотическое выражение:

Легко, верно?

Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?

Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:

Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:

Или, аналогично:

Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы — это очень просто. Да и перевод без проблем… И «Пи» — вполне терпимая штука… Так откуда путаница!?

Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов — пишется. Всегда. Например, sin35°. Это синус 35 градусов. А значок радианов (рад) — не пишется! Он подразумевается. То ли лень математиков обуяла, то ли ещё что… Но решили не писать. Если внутри синуса — котангенса нет никаких значков, то угол — в радианах! Например, cos3 — это косинус трёх радианов.

Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!

Ещё раз: «Пи» — это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…

«Пи» — это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?

или

 

Или, что меньше?

cos4°

или

cos4 ?

Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать…

Если вы тоже в ступор впали, вспоминаем заклинание: «Пи» — это число! 3,14. В самом первом синусе четко указано, что угол — в градусах! Стало быть, заменять «Пи» на 180° — нельзя! «Пи» градусов — это примерно 3,14°. Следовательно, можно записать:

Во втором синусе обозначений никаких нет. Значит, там — радианы! Вот здесь замена «Пи» на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:

multiurok.ru

Радианная и градусная меры угла

ГРАДУСНАЯ МЕРА УГЛА. РАДИАННАЯ МЕРА УГЛА. ПЕРЕВОД ГРАДУСОВ В РАДИАНЫ И ОБРАТНО.

ГРАДУСНАЯ МЕРА УГЛА.

Градусы придумали в Древнем Вавилоне.

Давненько это было… Веков 40 назад…

И придумали просто.

Взяли и разбили окружность на 360 равных частей.

1 градус — это 1/360 часть окружности.

И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360.

Где-то в то же время, в Древнем Египте мучились другим вопросом.

Во сколько раз длина окружности больше длины её диаметра?

И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно… Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя… В принципе нельзя.

Ну, во сколько раз окружность больше диаметра установили, конечно.

Примерно. В 3,1415926… раз.

Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.

Для практического применения принято запоминать всего две цифры после запятой.

Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:

Где L — длина окружности,

а d — её диаметр.

Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы.

Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена.

И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245… И что мне делать? Нет уж…»

Пришлось послушаться. Природу не обманешь…

Пришлось ввести меру угла, не зависящую от человеческих придумок.

Знакомьтесь — радиан!

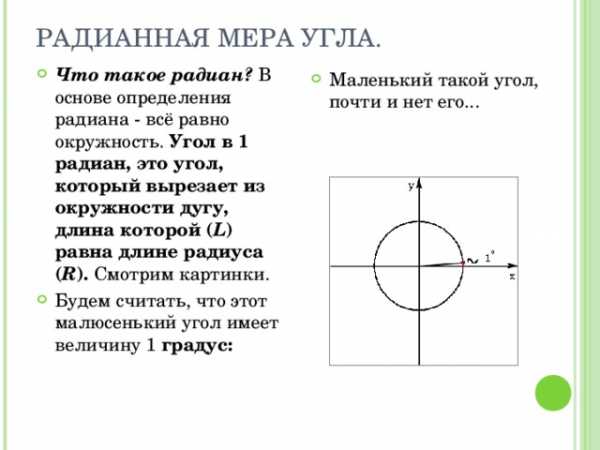
РАДИАННАЯ МЕРА УГЛА.

• Что такое радиан? В основе определения радиана — всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой ( L ) равна длине радиуса ( R ). Смотрим картинки.
• Будем считать, что этот малюсенький угол имеет величину 1 градус:

• Маленький такой угол, почти и нет его…

• Видим примерно один радиан . L = R

• Чувствуете разницу?
• Один радиан много больше одного градуса. А во сколько раз?

• Смотрим следующую картинку. На которой нарисован полукруг. Развёрнутый угол размером, естественно, в 180°.
• А теперь нарежем этот полукруг радианами! И видим, что в 180° укладывается 3 с хвостиком радиана.
• Кто угадает, чему равен этот хвостик!?
• Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!

Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:

Вот теперь совершенно осмысленно можно записать приближённое равенство:

Или точное равенство:

Определим, сколько градусов в одном радиане. Как? Легко!

Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:

• Это соотношение полезно запомнить. В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
• Но главное умение этой темы — перевод градусов в радианы и обратно.
• Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан ? Вот и пишем:

Или, более экзотическое выражение:

                                                         

• Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
• Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:

Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:

Отметим, что в тригонометрических функциях значок градусов — пишется. Всегда.

Например, sin35°. Это синус 35 градусов .

А значок радианов ( рад ) — не пишется!

Он подразумевается.

То ли лень математиков обуяла, то ли ещё что… Но решили не писать.

Если внутри синуса — котангенса нет никаких значков, то угол — в радианах ! Например, cos3 — это косинус трёх радианов .

Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!

Ещё раз : «Пи» — это число! 3,14.

Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…

Переведите эти углы из градусной меры в радианную:

360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°

Переведите эти углы из радианной меры в градусную:

multiurok.ru

Урок Радианная мера угла

Урок 2

Радианная мера углов и дуг

Для чего же нужна числовая окружность? Почему она так важна для науки вообще и для нас в частности? Начнем рассматривать области ее практического применения.

Как было сказано, числовая окружность используется, когда точка движется не прямолинейно, например, при изучении вращательного движения.

Движение точки по окружности можно представить двумя способами.

Во-первых, можно сказать, что точка В прошла по окружности путь t.

Во-вторых, можно сказать, что подвижный радиус ОВ образовал с неподвижным радиусом ОА угол t. Поскольку он получен поворотом радиуса ОВ, то он называется «угол поворота».

Результат будет один и тот же.

Кстати, подвижный радиус ОВ называется радиус–вектором точки В.

Таким образом, мы можем измерять движение точки по кругу с помощью угла, на который она повернулась. Т.е. для произвольного числа t мы построили угол t, определяемый двумя лучами – неподвижным и тем, который проходит через построенную точку.

При таком обобщении понятия угла постепенно отходят от его геометрического образа как части плоскости, лежащей между двумя лучами. Фактически слово «угол» становится для нас синонимом слова «число».

Теперь нужно выбрать меру измерения таких новых углов – углов поворота.

Понятие об измерении углов известно из геометрии. При измерении углов принимают некоторый определенный угол за единицу измерения и с ее помощью измеряют другие углы.

За единицу измерения можно принять любой угол:

• на практике уже более трех тысяч лет за единицу измерения величины угла принята ¹/₃₆₀ часть полного оборота, которую называют градусом;

• в технике за единицу измерения принимают полный оборот;

• в мореплавании за единицу измерения углов принят румб, равный
  ¹/₃₂ части полного оборота;

• в артиллерии за единицу измерения углов принята ¹/₆₀ часть полного оборота, которую называют большим делением угломера (¹/₁₀₀ часть большого деления угломера называют малым делением угломера).

Для измерения новых углов – углов поворота – привычные нам градусы не подходят, потому, что градусами измеряют только углы, а здесь одной меркой должны измеряться и углы, и расстояния.

Выход нашли Ньютон и Лейбниц — они стали измерять эти углы этими расстояниями.

Вопрос: «Чем измеряется расстояние на числовой окружности?»,

другими словами,

«Чему равен единичный отрезок числовой окружности?».

Так появилась универсальная мера измерения и углов, и дуг — радиусная мера или, как ее чаще называют, радианная мера.

Для закрепления изученного

материала рассмотреть ОК–3.

Ответить на вопросы 3, 4.

Еще раз подчеркнуть универсальность радианной меры, с помощью которой можно измерять и углы, и расстояния (дуги).

3. Какая величина принимается за единицу измерения при градусном измерении углов?

4. Что такое радиан?

Ответить на вопрос 8.

Отсюда истекает сложность, заключающаяся в двойственном применении числа  – рассмотреть примечание.

8. При каком условии длина дуги равна ее радианной мере?

Ответить на вопрос 7.

Дополнительный вопрос:

«А как построить угол, равный числу (–1)?»

7. Почему ошибочна запись  = 180?

Помимо того, что радианная мера лучше приспособлена для изучения криволинейного (кругового) движения, она существенно упростила многие расчеты и формулы:

длина дуги окружности: ;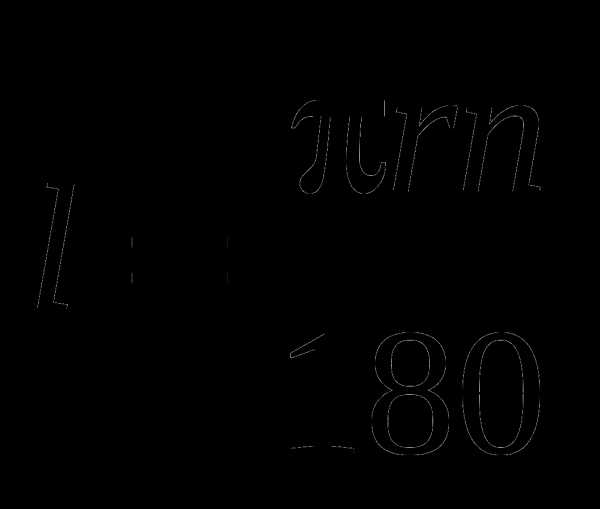

площадь сектора: .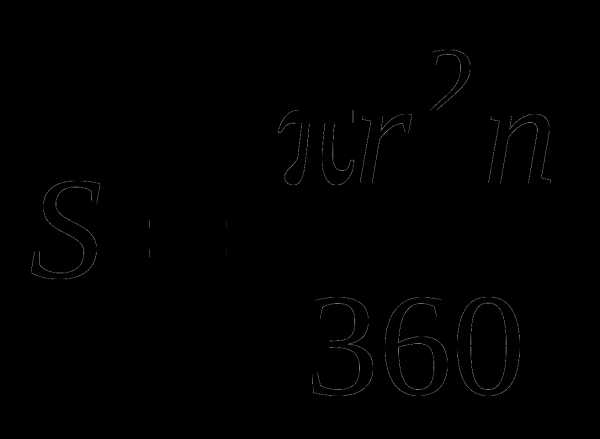

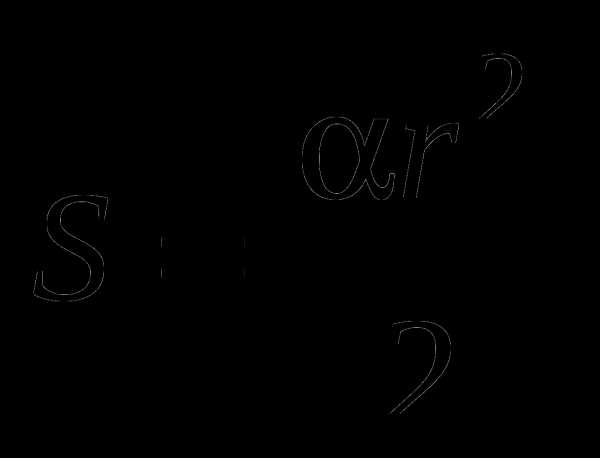Рассмотреть формулы перехода от градусной меры к радианной и наоборот.

Ответить на вопросы 5, 6.

5. По каким формулам переводят градусную меру угла в радианную и наоборот?

6. Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.

Решать задачи № 9(пр) – № 14(пр)

При решении № 13(пр) напомнить ученикам о правиле именования дуг, принятое нами на прошлом уроке.

9. Выразите в радианах:

1) 1; 4) 10; 7) 15; 10) 30;

2) 45; 5) 60; 8) 70; 11) 90;

3) 225; 6) 240; 9) 320; 12) 330.

10. Переведите из градусной меры в радианную:

1) 120; 3) 220; 5) 300; 7) 765;

2) 210; 4) 150; 6) 315; 8) 675.

11. Выразите в градусах:

1) ; 4) ; 7) ; 10) ;

2) ; 5) ; 8) 1,5; 11) 3;

3) 0,25; 6) ; 9) ^–; 12) .

12. Переведите из радианной меры в градусную:

1) ; 3) ; 5) ; 7) ;

2) ; 4) ; 6) ; 8) .

13. Окружность разделена на шесть равных частей. Выразить в градусах и радианах сумму дуг:

1) ;

2) .

14. Угол А трапеции ABCD (AD || BC) на 70 меньше угла В и на 10 больше угла D. Найдите радианную меру каждого из углов трапеции.

infourok.ru

8. Радианы, тригонометр.функции

Угол величиной в 1 радиан

1 радиан — величина центрального угла окружности, опирающегося на дугу, длина которой равна радиусу этой окружности.

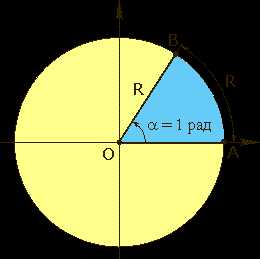
Примечание. Очевидно, что угол в радиан не меняется при переходе к другой окружности. Измерение углов радианами — пропорциональное, аналогичное измерению градусами или измерению отрезков единичными отрезками. Например, угол опирающийся на дугу, длина которой равна двум радиусам, будет иметь мерурадиана.

Радианная мера угла, то есть, выражение величины угла в радианах, имеет преимущества перед градусной мерой или любой другой: численное значение радианной меры дуги единичной окружности совпадает с длиной соответствующей дуги. Таким образом, радианная мера даёт возможность отождествить (не различать) измерение углов и отрезков.

Перевод из градусной меры в радианную

Центральный угол окружности, равный , опирается на полуокружность. Длина полуокружности единичного радиуса равна. Следовательно,рад. В силу принципа пропорциональности радианной меры, получаем формулу для перевода градусной меры произвольного угла в радианную:рад.

Пример. Дан угол радрад.

Перевод из радианное меры в градусную

Центральный угол окружности, равный , опирается на полуокружность. Длина полуокружности единичного радиуса равна. Следовательно,рад. В силу принципа пропорциональности радианной меры, получаем формулу для перевода градусной меры произвольного угла в радианную:.

Пример. Дан угол рад. Выразить его величину в градусах.

Решение. рад.

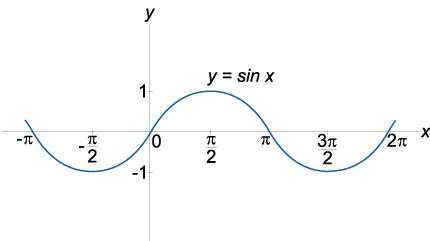
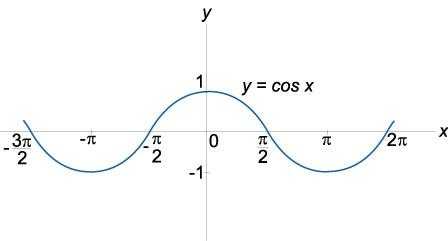
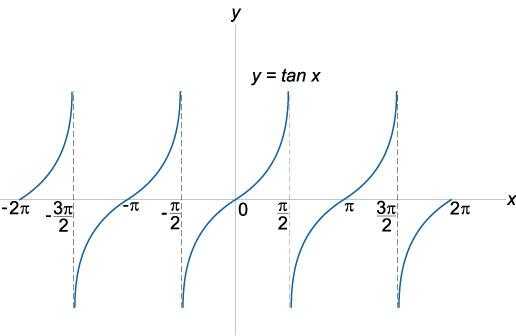
Определение и графики тригонометрических функций

Величины углов (аргументы функций): α, x Тригонометрические функции: sin α, cos α, tan α, cot α, sec α, cosec α Множество действительных чисел: ℜ Координаты точки окружности: x, y Радиус круга: r Целые числа: k Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решениидифференциальныхи функциональных уравнений. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r = 1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: sin α = y/r. Поскольку r = 1, то синус равен ординате точки M(x,y). Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: cos α = x/r = x Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: tan α = y/x,   x ≠ 0 Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: cot α = x/y,   y ≠ 0 Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): sec α = r/x = 1/x,   x ≠ 0 Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): cosec α = r/y = 1/y,   y ≠ 0 В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x, y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: Синусом угла α называется отношение противолежащего катета к гипотенузе. Косинусом угла α называется отношение прилежащего катета к гипотенузе. Тангенсом угла α называется противолежащего катета к прилежащему. Котангенсом угла α называется прилежащего катета к противолежащему. График функции синус y = sin x, область определения: x ∈ ℜ, область значений: −1 ≤ sin x ≤ 1 График функции косинус y = cos x, область определения: x ∈ ℜ, область значений: −1 ≤ cos x ≤ 1 График функции тангенс y = ttg x, область определения: x ∈ ℜ, x ≠ (2k + 1)π/2, область значений: −∞ < tg x < ∞ График функции котангенс y = ctg x, область определения: x ∈ ℜ, x ≠ kπ, область значений: −∞ < ctg x < ∞

Формулы приведения

  

   Основные тригонометрические тождества

studfiles.net