Расчет площади геометрических фигур | International Institute of Care to Buildings
СПРАВОЧНИКИ
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.
Формулы площади треугольника
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См. также: Онлайн калькулятор для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Онлайн кальклятор для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Онлайн калькулятор для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Онлайн калькулятор для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Онлайн калькулятор для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Онлайн калькулятор для расчета площади ромба.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
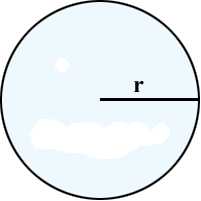
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Онлайн калькулятор для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
См. также: Онлайн калькулятор для расчета площади эллипса.
miuz.org
Площади и объемы
Площади
История нахождения площадей фигур начинается еще с древнего Вавилона. Уже тогда вычисляли площади прямоугольника, а древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.
Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.
Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.
Формула площади прямоугольника
Рассмотрим фигуру (рис. 1), которая состоит из $8$ квадратов со сторонами по $1$ см. Площадь одного квадрата со стороной $1$ см называют сантиметром квадратным и записывают $1\ см^2$.
Площадь данной фигуры (рис. 1) будет равна $8\ см^2$.
Площадь фигуры, которую можно разбить на несколько квадратов со стороной $1\ см$ (например, $p$), будет равна $p\ см^2$.
Другими словами, площадь фигуры будет равна стольким $см^2$, на сколько квадратов со стороной $1\ см$ можно разбить эту фигуру.
Рассмотрим прямоугольник (рис. 2), который состоит из $3$ полос, каждая из которых разбита на $5$ квадратов со стороной $1\ см$. весь прямоугольник состоит из $5\cdot 3=15$ таких квадратов, и его площадь равна $15\ см^2$.
Рисунок 1.
Рисунок 2.
Площадь фигур принято обозначать буквой $S$.
Для нахождения площади прямоугольника нужно его длину умножить на ширину.
Если обозначить буквой $a$ его длину, а буквой $b$ — ширину, то формула площади прямоугольника будет иметь вид:
Определение 1
Фигуры называют равными, если при наложении их одна на другую фигуры совпадут. Равные фигуры имеют равные площади и равные периметры.
Площадь фигуры можно найти как сумму площадей ее частей.
Пример 1
Например, на рисунке $3$ прямоугольник $ABCD$ разбит на две части линией $KLMN$. Площадь одной части равна $12\ см^2$, а другой — $9\ см^2$. Тогда площадь прямоугольника $ABCD$ будет равна $12\ см^2+9\ см^2=21\ см^2$. Найдем площадь прямоугольника по формуле:
\[S=a\cdot b=3\cdot 7=21\ см^2.\]Как видим, площади, найденные обоими способами, равны.
Рисунок 3.
Рисунок 4.
Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.
Определение 2
Прямоугольник с равными сторонами называется квадратом.
Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:
\[S=a\cdot a=a^2.\]Отсюда и название квадрат числа $a$.
Пример 2
Например, если сторона квадрата равна $5$ см, то его площадь:
\[S=a^2=5^2\ см^2=25\ см^2.\]Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.
Объем измеряется с помощью следующих единиц:
$мм^3$ — миллиметр кубический,
$см^3$ — сантиметр кубический,
$дм^3$ — дециметр кубический,
$м^3$ — метр кубический,
$км^3$ — километр кубический.
Пример 3
Например, сантиметр кубический — это объем куба с ребром $1\ см$ (рис.~6).
Замечание 1
Дециметр кубический еще называют литром.
\[1\ л=1\ дм^3.\]На рисунке $7$ фигура состоит из $4$ кубиков с ребром $1\ см$. объем такой фигуры равен $4\ см^3$.
Рисунок 6.
Рисунок 7.
Рассмотрим прямоугольный параллелепипед длиной $4$ см, шириной $3$ см и высотой $2$ см (рис. 8, а). Разделим его на $2$ слоя толщиной $1$ см (рис. 8, б).
Разделим каждый из слоев на $3$ столбика длиной $4$ см (рис. 8, в), а каждый столбик — на $4$ кубика с ребром $1$ см (рис. 8, г).
Рисунок 8.
Объем каждого кубика равен $1\ см^3$, объем каждого столбика — $4\cdot 1\ см^3=4\ см^3$, объем каждого слоя — $3\cdot 4\ см^3$. Тогда объем всего прямоугольного параллелепипеда — $2\cdot \left(4\cdot 3\right)\ см^3=24\ см^3$.
Таким образом, для вычисления объема прямоугольного параллелепипеда нужно его длину умножить на ширину и на высоту.
Объем фигуры принято обозначать буквой $V$.
Формула объема прямоугольного параллелепипеда:
Определение 3
Куб — прямоугольный параллелепипед с равными ребрами.
Если ребро куба равно $a$, то формула объема куба будет иметь вид:
\[V=a\cdot a\cdot a=a^3.\]Отсюда и название куб числа $a$.
spravochnick.ru
Калькулятор для расчета площади различных геометрических фигур
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Полезные калькуляторы
Расчет площади прямоугольника
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади треугольника
Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними
Вычислить
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади правильного многоугольника
Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r
Вычислить
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади круга
Рассчитать площадь круга, если известен:
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади эллипса
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
|
r= ммсммкмфутярддюйммиля |
|
|
θ= ммсммкмфутярддюйммиля град.рад. |
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади трапеции
Способ нахождения площади треугольника: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр — 1 км2 = | 1 000 000 м2 |
| Гектар — 1 га = | 10 000 м2 |
| Ар (сотка) — 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
remont-otdelka-m.ru
Калькулятор вычисления объема и площади геометрических фигур
Весь осязаемый мир представляет собой объемные геометрические фигуры и их сочетания. Определение объемов и площадей поверхностей тел может понадобиться не только при решении школьных задач, но также в быту или профессиональной деятельности. Простые объемные тела разделяются на две категории.
Тела вращения
Первая категория — это тела вращения. Такие объемные фигуры образуются путем вращения плоской фигуры вокруг одной из сторон или путем движения образующей кривой вдоль направляющей. Наш каталог предлагает калькуляторы, при помощи которых можно рассчитать параметры следующих тел вращения.
Конус
Конус — фигура, которая создается путем вращения прямоугольного треугольника вокруг одного из катетов. Также конус формируется путем движения образующего луча вдоль направляющей окружности, при этом начало луча остается неподвижным. Для определения площади поверхности конуса используется простая формула:
S = pi × R × (R + l),
где R — радиус основания, l — образующая конуса.
Для подсчета объема конической фигуры используется следующее соотношение:
V = (pi × R 2 × h)/3,
где h — высота конуса.
Конусы широко встречаются в быту, производстве или науке. Например, коническую форму имеют вафельные рожки для мороженного, абажуры для светильников, пожарные ведра или воронки. В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
Цилиндр
Цилиндр — тело вращения, которое образуется путем вращения прямоугольника вокруг одной из сторон. Также цилиндр формируется путем движения образующей прямой по направляющей кривой, которая в случае цилиндра может быть окружностью, эллипсом, параболой или гиперболой. Такие «экзотические» цилиндры носят соответствующие названия эллиптических, параболических и гиперболических фигур, однако в реальной жизни наибольшее распространение получил прямой круговой цилиндр. Для определения площади поверхности такого цилиндра используется формула:
S = 2 pi × R × (R + h),
где R — радиус основания, h — высота цилиндра.
Для вычисления объема цилиндра геометры применяют следующее соотношение:
V = pi × R2 × h.
Цилиндр легко встретить в реальной жизни: это и цистерны, и поршни двигателей, и колонны, и трубы газопроводов. Цилиндры широко используются в производстве, поэтому многим инженерам приходится вычислять площади поверхностей или объемы цилиндрических объектов.
Шар
Шар — тело вращения, созданное путем вращения круга около своей оси. Сфера — это поверхность, сформированная путем вращения окружности или полуокружности вокруг своей оси. Таким образом, шар — это пространство, ограниченное сферой. Площадь сферы вычисляется по формуле:
S = 4 pi × R2,
где R — радиус сферы.
Для подсчета объема шара используется следующее выражение:
V = 4/3 pi × R3.
Шар — идеальная фигура, поэтому в природе она встречается довольно часто. К примеру, сферическую форму принимают капли дождя, снежные комья, планеты, звезды, а также ягоды или кроны деревьев. В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
Многогранники
Вторя категория — многогранники. Многогранник или полиэдр — это объемное тело, каждая грань которого является многоугольником. Существует огромное множество многогранников: к ним относятся призмы, пирамиды, параллелепипеды, а также платоновы тела — полиэдры, гранями которых являются правильные многоугольники. В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
Призма
Призма — это полиэдр, который состоит из двух n-угольных оснований, параллельных друг другу и n боковых граней, формирующих боковую поверхность призмы. Грань призмы — это всегда параллелограмм. Простыми словами, если в основании фигуры лежит квадрат, то призма считается четырехугольной, но при этом шестигранной: четыре грани составляют боковую поверхность, а две — поверхность оснований. Если в основании лежит пентагон — то призма пятиугольная и семигранная, а если додекагон — то фигура 12-угольная и 14-гранная. Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
Sb = n × a × h,
где a — сторона параллелограмма, n — количество граней, h — его высота.
Площадь поверхности основания призмы зависит от многоугольника и в общем виде для правильных полигонов рассчитывается как:
So = n/4 × a2 × ctg(pi/n),
где n — количество сторон фигуры, a — длина стороны.
Полная же площадь поверхности определяется как:
S = 2 So + Sb.
Объем призмы вычисляется по следующей формуле:
V = So х h.
Призма — наиболее распространенный в человеческой повседневности полиэдр. Форму призмы имеет огромное число предметов вокруг вас: это системный блок компьютера, сабвуфер, стол, шкаф, комната и здание. Если выйти на улицу, то вы увидите царство призм. Именно поэтому инструмент для определения объемов и площадей поверхности призматических фигур всегда актуален.
Пирамида
Пирамида — это полиэдр, который составлен из n-угольного основания и n боковых граней, формирующих боковую поверхность пирамидальной фигуры. Грань пирамиды — это всегда треугольник. Вид полиэдра определяется в зависимости от того, какой полигон выступает в роли фундамента пирамиды. Следовательно, пирамиды бывают треугольные, четырехугольные, пятиугольные или n-угольные. Площадь боковой порвехности пирамиды рассчитывается согласно выражению:
Sb = 0,5 P х h,
где h — высота пирамиды, P — периметр полигона, лежащего в основании.
Площадь фундамента рассчитывается по общей формуле для любого правильного полигона:
So = n/4 × a2 × ctg(pi/n),
где a — длина стороны, n — количество сторон.
Полная площадь поверхности пирамиды определяется как:
S = So + Sb.
Для определения объема пирамиды используется формула:
V = (So х h)/3,
где h — высота фигуры.
Пирамида — довольно распространенная фигура и широко используется в архитектуре. Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Параллелепипед
Параллелепипед — это гексаэдр с попарно параллельными гранями. Если ребра такого шестигранника равны, то параллелепипед превращается в куб. Параллелепипед — это частный случай прямой четырехугольной призмы, поэтому формулы для расчета площади и объема фигуры выводятся из соотношений для призмы с n = 4. Таким образом, для расчета площади поверхности гексаэдра используется формула:
S = 4 (a × h) + 2 (a × b),
где a, b — стороны основания параллелепипеда, h — высота фигуры.
Объем полиэдра определяется как:
V = a × b × h.
Параллелепипед, так же как и призма, постоянно встречается в реальности. Форму такого гексаэдра имеет множество вещей вокруг нас: шлакоблоки, бетонные плиты, грузовые контейнеры или картонные коробки. Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Примеры использования
Наш калькулятор позволяет рассчитать объем или площадь поверхности любого из заданных геометрических тел. Рассмотрим пару примеров.
Заливка бетона
К примеру, вы решили построить летний коттедж, а для каждого дома необходим фундамент. Вы выбрали плитный фундамент — монолитную плиту, которую заливают под всей площадью будущего жилища. Вам требуется узнать, сколько бетона понадобится для обустройства такого фундамента. Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
V = 8,1
Таким образом, нам потребуется заказать 8,1 кубометров бетонной смеси.
Пошив мячей
Допустим, вы открыли производство по производству волейбольных мячей, и вам требуется узнать, сколько материала уходит на пошив одного мяча. Согласно данным из Википедии, стандартный волейбольный мяч имеет длину окружности l = 67 см, следовательно, радиус такого мячика составит 10,6 см. Зная радиус, вы без проблем можете определить, сколько синтетической кожи понадобится для создания одного изделия
S = 0,141
Это означает, что для обшивки одного мяча вам понадобится 0,141 квадратных метров кожи.
Заключение
Объемные фигуры постоянно вращаются вокруг нас, поэтому задача определения площадей поверхностей и объемов многогранников остается актуальной задачей. Используйте наш каталог онлайн-калькуляторов и выполняйте необходимые расчеты для решения бытовых или производственных задач.
bbf.ru
Расчет Геометрических Фигур | Онлайн калькулятор
Allcalc Geometry на сегодняшний день является одним из самых мощных приложений в решении геометрических задач.Содержит более 800 формул, в том числе и формулы для обратного расчета, объединенные в 144 калькулятора.
Калькулятор Геометрических Фигур рассчитывает: Площадь, Объем, Угол, Диагональ, Высоту, Радиус вписанной окружности, Радиус описанной окружности, Катет, Гипотенузу, Радиус описанной сферы, Радиус вписанной сферы, Сторону, Медиану, Биссектрису, Площадь основания, Площадь поверхности, Площадь осевого сечения, Площадь боковой поверхности, Площадь грани, Сторону основания, Периметр, Периметр основания, Радиус, Грань, Ребро, Апофему, Дугу, Угол наклона грани, Угол наклона ребра, Угол наклона образующей, Угол между диагоналями, Угол от деления диагональю, Угол дуги, Угол сторон, Угол раствора, Боковое ребро, Среднюю линию, Диаметр, Окружность, Радиус основания, Хорду, Сегмент, Сектор, Образующею, Осевое сечение, Диагональ осевого сечения, оси, Диагональ грани.
Плоские фигуры: Круг, Ромб, Треугольник, Прямоугольник, Трапеция, Квадрат, Параллелограмм, Кольцо, Сектор круга, Сегмент круга, Эллипс.
Объемные тела: Цилиндр, Куб, Шар (Сфера), Параллелепипед, Пирамида, Призма, Конус, Тетраэдр, Усеченная пирамида, Усеченный конус, Октаэдр.
Приложение поддерживает мобильную платформу Android от Google.
Рекомендуем к просмотру видео:
Перейти к установке приложения
Приведем примеры геометрических задач, которые решает калькулятор:
Зная радиус основания и высоту цилиндра можно вычислить: Объем цилиндра V, Площадь цилиндра S, Площадь боковой поверхности S, Площадь основания S, Площадь осевого сечения S, Диагональ осевого сечения d, Окружность основания P, Диаметр основания D, Радиус вписанной сферы, Радиус описанной сферы.
Помните, калькулятор содержит формулы обратного расчета, что означает следующие: зная высоту и площадь основания цилиндра можно вычислить объем, радиус, диагональ и т.д.
allcalc.ru
Площадь геометрической фигуры
Что такое площадь
Площадь геометрической фигуры — это неотрицательная численная величина, которая характеризует размер этой фигуры.Изначально, геометрия в Древней Греции (по-гречески «землемерие») занималась измерением площадей и объемов. Значительное число задач в области элементарной геометрии посвящено именно таким вопросам.
Общим методом нахождения площадей фигур в координатной плоскости является интегральное исчисление. Этими вопросами занимается математический анализ.
Для понимания применения универсального метода математического анализа для определения площади фигур можно привести следующие примеры вычисления площади:
- Площадь фигуры, заключенная между графиком непрерывной функции на интервале [a,b] и осью абсцисс, равна определенному интегралу этой функции на том же интервале
- Площадь фигуры, заключенная между графиками двух непрерывных функций на интервале [a,b] равна разности определенных интегралов этих функций на этом интервале
Или, с помощью формул это будет выглядеть следующим образом:
Как видно из рисунка и из формул, площадь фигуры, заключенной между графиком непрерывной функции f(x) и осью координат x на интервале [a,b] равна определенному интегралу этой функции [1].
Если же нам необходимо найти площадь фигуры, заключенной между графиками двух непрерывных функций — мы просто находим определенный интеграл для обоих функций и вычитаем площадь одной фигуры из площади другой. Разность площадей и даст нам искомую величину.
С помощью интегрального исчисления также определяются площади поверхностей фигур и в полярных координатах (фигура, заключенная между двумя лучами) и в трехмерном пространстве.
Свойства площади фигур
Площадь фигуры – это неотрицательная величина, числовое значение которой имеет следующие свойства:- Площадь фигуры является неотрицательной величиной
- Равные фигуры имеют равные площади
- Площадь фигуры равна сумме составляющих ее и не перекрывающих друг друга частей (свойство аддитивности).
- Площадь квадрата со стороной, равной единице измерения, равна единице (свойство нормированности)
- Площадь фигуры всегда больше площади ее части (свойство монотонности)
Формулы для нахождения площадей геометрических фигур
Площадь квадрата со стороной а
S=a2
См. также — квадрат и площадь квадрата. Все формулы.
Площадь прямоугольника со сторонами а и b
S=ab
См. также Задачи про нахождение площади прямоугольника с пояснениями.
Площадь параллелограмма со сторонами а и b или с основанием а и высотой h
S=ah
S=ab*sin ∠ab
См. также свойства и площадь параллелограмма.
Площадь ромба со стороной а, углом между сторонами α, диагоналями d1, d2
S=ab*sinα
или
S=1/2 d1d2
См. также Задачи о ромбе.
Площадь треугольника с основанием а и высотой h
S=1/2 ah
См. также площадь треугольника (все формулы).
Площадь трапеции с основанием а, b и высотой h
S=(a+b)/2 * h
См. также свойства и площадь трапеции (все формулы).
Площадь круга
S=πR2
См. также Задачи про окружность.
profmeter.com.ua
Функции вычисления площади геометрических фигур
Паскаль сам по себе не предоставляет функции, вычисляющей площадь круга по фактическому параметру – диаметру круга. Однако такую функцию легко определить самостоятельно. После этого функцию, например, circle можно использовать в программе точно так же, как ранее использовались функции sqr или trunc.
В первой строке определения функции параметр d как бы говорит «Делай то, что делается со мной, но используй значение, которое будет на моем месте». При вызове функции на местоd ставится число, которое таким образом возводится в квадрат, затем результат умножается на 3.14159 и делится на 4.0. Параметр d – это формальный параметр, тогда как конкретное число – фактический параметр. В основной программе, обращающейся к функции circle, можно использовать имя d как имя переменной (или любого другого объекта), не опасаясь помех со стороны функции.
Также приведены функции, вычисляющие площади прямоугольника и треугольника; их параметрами являются длины сторон.
Все эти функции могут быть вызваны из программы в любой последовательности и любое количество раз.
Обратите внимание на то, что функции вызываются с фактическими параметрами x, y, z, тогда как формальные параметры в их определениях – a, b, c, d. Переменная a в основной программе никак не связана с формальным параметром a в функциях. Точно так же отсутствует связь переменной x в основной программе и локальной переменной x в функции triangle.
Определенные здесь функции различаются по числу параметров. В функциях может быть любое фиксированное число параметров; определить функцию с переменным числом параметров (например, как в случае read(a), read(a, b), read(a, b, c)) нельзя – такой возможностью пользуется только сам Pascal.
Программа на языке Паскаль:
var
choice: char;
a, x, y, z: real;
function circle(d: real): real;
const pi = 3.14159;
begin
circle := pi * sqr(d) / 4.0;
end;
function rectangle(a, b: real): real;
begin
rectangle := a * b
end;
function triangle(a, b, c: real): real;
var x: real;
begin
x := (a + b + c) / 2;
triangle := sqrt(x * (x - a) * (x - b) * (x - c))
end;
begin
repeat
read(choice);
case choice of
'c': begin
readln(x);
a := circle(x)
end;
'r': begin
readln(x, y);
a := rectangle(x, y)
end;
't': begin
readln(x, y, z);
a := triangle(x, y, z)
end
end;
writeln('Square: ', a:8:2);
until choice = 'q';
readln
end.
pas1.ru
