Площадь трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
x2-(d-b-x)2=a2-c2 — Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 — Раскрываем скобки.
x2-d2+2bd+2dx-b2-2bx-x2=a2
2dx-2bx=a2-c2+d2+b2-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 — Выносим общие множители.
Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
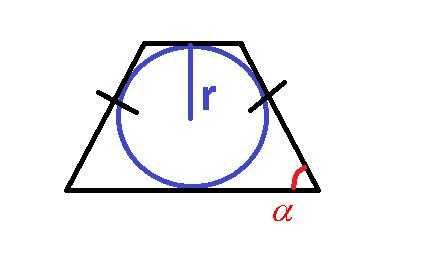
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону и среднюю линию
geleot.ru
Калькулятор площади трапеции онлайн
Формула площади трапеции S = 1/2 × (a + b) × hГде a и b — это основания, h — высота трапеции.
Подставте в поля нужные величины и нажмите «Расчитать» Поделитесь с друзьями в соцсетях…
Похожее
kalkulyator.life
Площадь трапеции
Площадь трапеции, формулы и калькулятор для вычисления площади в режиме онлайн. Приведены формулы для всех типов трапеций и частные случаи для равнобедренных трапеций.
Площадь для всех видов трапеции
1
Площадь трапеции по высоте и двум основаниям
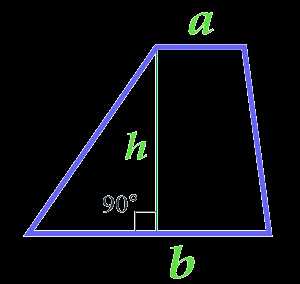
a — основание
b — основание
h — высота
… подготовка …
2
Площадь трапеции по высоте и средней линии

m — средняя линия
h — высота
… подготовка …
3
Площадь трапеции по четырем сторонам

a — основание
b — основание
c — сторона
d — сторона
… подготовка …
4
Площадь трапеции по диагонали и углу между диагоналями
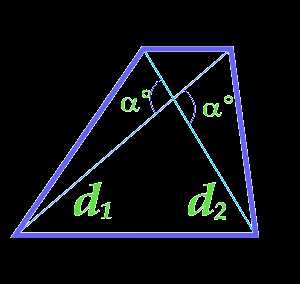
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
… подготовка …
5
Площадь трапеции через ее основания и углы при основании
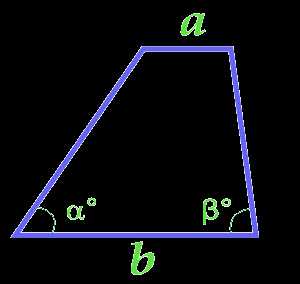
a — основание
b — основание
α° — угол при основании
β° — угол при основании
… подготовка …
Площадь равнобедренной трапеции
6
Площадь равнобедренной трапеции через ее стороны
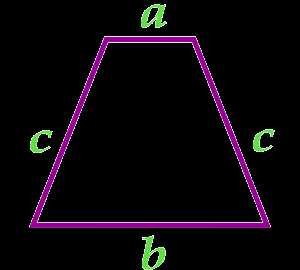
a — сторона
b — сторона
c — сторона
… подготовка …
7
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании
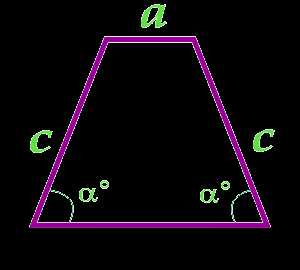
a — основание
c — сторона
α° — угол при основании
… подготовка …
8
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол при большем основании
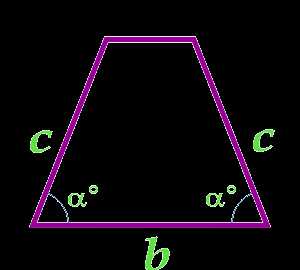
b — основание
c — сторона
α° — угол при основании
… подготовка …
Площадь равнобедренной трапеции через основания и угол при основании
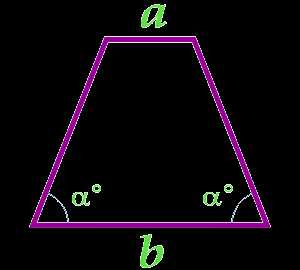
a — основание
b — основание
α° — угол при основании
… подготовка …
10
Площадь равнобедренной трапеции через диагонали и угол между диагоналями
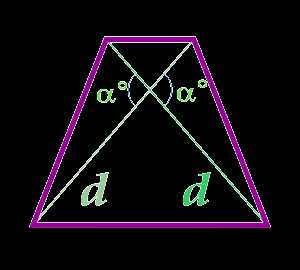
d — диагональ
α° — угол между диагоналями
… подготовка …
11
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
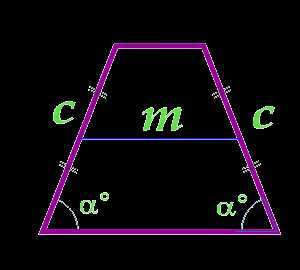
m — средняя линия
c — сторона
α° — угол между сторонами
… подготовка …
12
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами
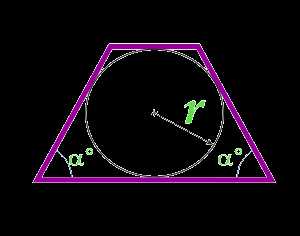
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
r — радиус вписанной окружности
α° — угол между сторонами
… подготовка …
13
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
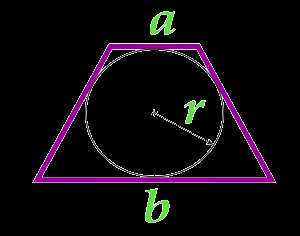
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
a — основание
b — основание
r — радиус вписанной окружности
… подготовка …
14
Площадь равнобедренной трапеции через ее основания и угол при большем основании
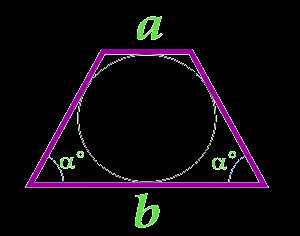
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
a — основание
b — основание
α° — угол при основании
… подготовка …
15
Площадь равнобедренной трапеции через стороны
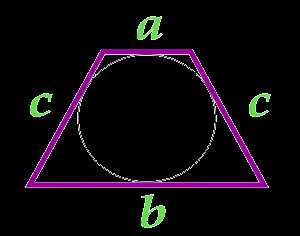
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
a — основание
b — основание
c — сторона
… подготовка …
16
Площадь равнобедренной трапеции через основания и среднюю линию
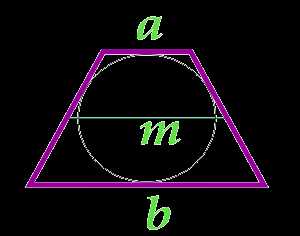
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
a — основание
b — основание
m — средняя линия
… подготовка …
Определения
Площадь трапеции – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу
Трапеция – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу.
Основания трапеции – это параллельные стороны трапеции. Трапеция имеет большое и малое основание.
Средняя линия трапеции
Высота трапеции – это отрезок проведенный между основаниями трапеции под углом 90 градусов к каждому из снований.
Сумма углов трапеции равна 360 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
doza.pro
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины
Расчет площади прямоугольника
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади треугольника
Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними
ВычислитьРезультат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади круга
Рассчитать площадь круга, если известен:
ВычислитьРезультат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади правильного многоугольника
Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r
ВычислитьРезультат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади эллипса
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
|
r= ммсммкмфутярддюйммиля |
|
|
θ= ммсммкмфутярддюйммиля град.рад. |
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади трапеции
Способ нахождения площади трапеции: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр — 1 км2 = | 1 000 000 м2 |
| Гектар — 1 га = | 10 000 м2 |
| Ар (сотка) — 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
calc.by
Все формулы площади трапеции. Найти онлайн
Формулы площади трапеции
Внимание! Десятичную дробь надо писать с точкой, а не с запятой!
Трапеция — четырехугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами.
Площадь трапеции через основания и высоту
$$S= \frac{a+b}{2}h $$ \(S\) — площадь трапеции\(a\) — основание
\(b\) — основание
\(h\) — высота
\(a =\) \(b =\) \(h =\)
Площадь трапеции через высоту и среднюю линию
$$S= mh $$ \(S\) — площадь трапеции\(h\) — высота
\(m\) — средняя линия трапеции
\(h =\) \(m =\)
Площадь трапеции через четыре стороны
$$S= \frac{a+b}{2} \sqrt{c^2-\left( \frac{(b-a)^2+c^2-d^2}{2(b-a)} \right)^2}$$ \(S\) — площадь трапеции\(a, b, c, d\) — стороны
\(a =\) \(b =\)
\(c =\) \(d =\)
Площадь трапеции через диагонали и угол между ними
$$S= \frac{1}{2}d_1d_2sin \alpha $$ \(S\) — площадь трапеции\(d_1, d_2\) — диагонали
\(\alpha\) — угол между диагоналями \(d_1\) и \(d_2\)
\(d_1 =\) \(d_2 =\) \(\alpha = \)
Для равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол
$$S= \frac{4r^2}{sin \alpha}$$ \(S\) — площадь трапеции\(r\) — радиус вписанной окружности
\(\alpha\) — угол
\(r =\) \(\alpha =\)
www.100formul.ru
Площадь трапеции, онлайн калькулятор
Наш онлайн калькулятор позволяет вычислить площадь трапеции двумя способами: через основания и высоту или через среднюю линию и высоту. Для того чтобы найти площадь трапеции выберите подходящий способ, заполните соответствующие поля и нажмите кнопку «Вычислить», калькулятор покажет ответ и пошаговое решение!
Введите данные для расчета площадиВыберите cпособ расчета площади:
через основания и высоту через среднюю линию и высоту
Формула через основания и высоту: |
| Понравился сайт? Расскажи друзьям! | |||
Как найти площадь трапеции
Данный онлайн калькулятор дает возможность быстро и без проблем высчитать площадь любой трапеции. Вам надо знать только один из наборов параметров:
- Основание и высоту, что чаще всего и применяется;
- Среднюю линию и высоту.
Справка: средняя линия – это линия разделяющая трапецию поперек ровно по центру. Разделите боковые стороны пополам и проведите между ними линию. Это и будет та самая средняя линия, которая потребуется для того, чтобы узнать площадь всей трапеции.
Введите имеющиеся параметры в отдельные окошки и нажмите на кнопку «Вычислить». Теперь вы знаете, как имея на руках 2 значения всего за 2 клика легко и быстро посчитать площадь трапеции.
ru.solverbook.com
Найти площадь трапеции онлайн калькулятор.
Общая теория для вычисления площади трапеции.
Трапеция – это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции.
Две не параллельные стороны трапеции называются боковыми сторонами трапеции.
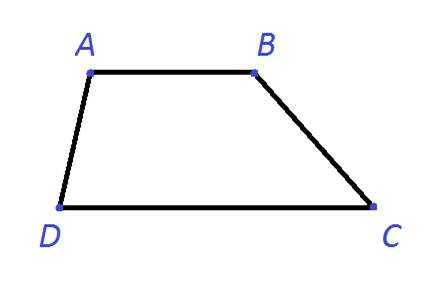
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC – основания трапеции ABCD.
AD, BC – боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
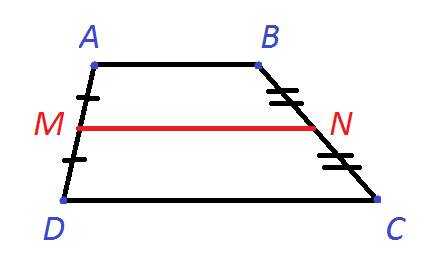
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
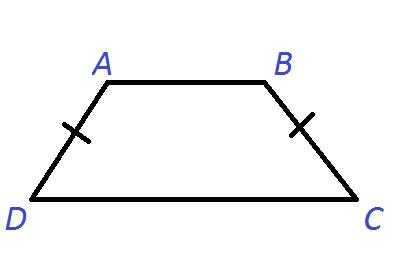
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой), если ее боковые стороны равны.
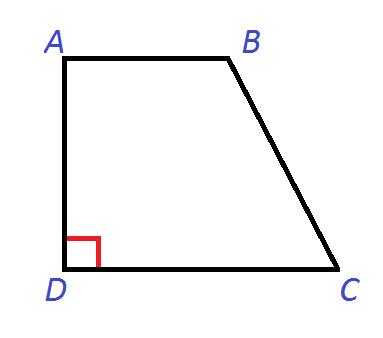
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D – прямой (равен 90о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
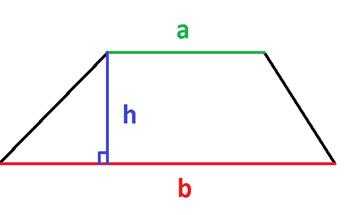
2. Площадь трапеции равна произведению ее средней линии на высоту:
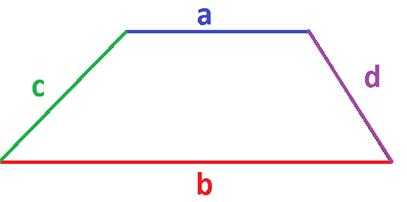
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см2, высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 7: Вычислить площадь трапеции с основаниями a=2, b=6 и боковыми сторонами c=3, d=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 8: Вычислить площадь равнобедренной трапеции с радиусом вписанной окружности r=9 и углом при основании трапеции α=30о.
Решение:
Для нахождения площади равнобедренной трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 9: Вычислить радиус вписанной в равнобедренную трапецию окружности, если площадь трапеции S=200 и углом при основании трапеции α=30о.
Решение:
Для нахождения радиуса вписанной в равнобедренную трапецию окружности воспользуемся следующей формулой вычисления площади:
Выразим из данной формулы радиус:
Таким образом, имеем следующее:
Ответ:
Пример 9: Вычислить угол при основании трапеции, считая, что он острый. Если радиус вписанной в равнобедренную трапецию окружности r = и площадь трапеции S=.
Решение:
Для нахождения угла при основании трапеции воспользуемся следующей формулой вычисления площади:
Выразим из данной формулы угол при основании трапеции:
Таким образом, имеем следующее:
Ответ:
ktoreshit.ru
