Квадратные уравнения с ответами 8 класс – Тест Квадратные уравнения (8 класс) с ответами и решением онлайн по алгебре

Урок по теме «Решение квадратных уравнений». 8-й класс

Разделы: Математика

---

Рассмотрим стандартные (изучаемые в школьном курсе математики) и нестандартные приёмы решения квадратных уравнений.

1. Разложение левой части квадратного уравнения на линейные множители.

Рассмотрим примеры:

3) х² + 10х – 24 = 0.

6(х² + х – х ) = 0 | : 6

х² + х – х – = 0;

х(х – ) + (х – ) = 0;

х(х – ) (х + ) = 0;

= ; – .

Ответ: ; – .

Для самостоятельной работы:

Решите квадратные уравнения, применяя метод разложения левой части квадратного уравнения на линейные множители.

а) х2 – х = 0; г) х2 – 81 = 0; ж) х2 + 6х + 9 = 0;

б) х2 + 2х = 0; д) 4х2 – = 0; з) х2 + 4х + 3 = 0;

в) 3х2 – 3х = 0; е) х2 – 4х + 4 = 0; и) х2 + 2х – 3 = 0.

Ответы:

а) 0; 1 г) ± 9 ж) – 3

б) -2; 0 д) з) -3; -1

в) 0; 1 е) 2 и) -3; -1

2. Метод выделения полного квадрата.

Рассмотрим примеры:

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод выделения полного квадрата.

3. Решение квадратных уравнений по формуле.

ах² + вх + с = 0, (а | · 4а

4а²х² + 4ав + 4ас = 0;

2ах + 2ах·2в + в² – в² + 4ас = 0;

² = в² – 4ас;

= ± ;

2ах = -в ±;

х_1,2 =.

Рассмотрим примеры.

Для самостоятельной работы.

Решите квадратные уравнения, применяя формулу х_1,2 =.

4. Решение квадратных уравнений с использованием теоремы Виета (прямой и обратной)

x² + px +q = 0 – приведённое квадратное уравнение

по теореме Виета.

Если то уравнение имеет два одинаковых корня по знаку и это зависит от коэффициента .

Если p, то .

Если p, то.

Например:

Если то уравнение имеет два различных по знаку корня, причём больший по модулю корень будет , если p и будет , если p.

Например:

Для самостоятельной работы.

Не решая квадратного уравнения, по обратной теореме Виета определите знаки его корней:

Ответы:

а, б, к, л – различные корни;

в, д, з – отрицательные;

г, е, ж, и, м – положительные;

5. Решение квадратных уравнений методом “переброски”.

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод “переброски”.

6. Решение квадратных уравнений с применением свойств его коэффициентов.

I. ax² + bx + c = 0, где a ⁰

1) Если а + b + с = 0, то х₁ = 1; х₂ =

Доказательство:

ax² + bx + c = 0 |: а

х² + х + = 0.

По теореме Виета

По условию а + b + с = 0, тогда b = -а – с. Далее получим

Из этого следует, что х₁ =1; х₂ = . Что и требовалось доказать.

2) Если а – b + с = 0 (или b = а +с ) , то х₁ = – 1; х₂ = –

Доказательство:

По теореме Виета

По условию а – b + с = 0 , т.е. b = а +с . Далее получим:

Поэтому х₁ = – 1; х₂ = – .

Рассмотрим примеры.

1) 345 х² – 137 х – 208 = 0.

а + b + с = 345 – 137 – 208 = 0

х_{1 =} 1; х₂ = =

Ответ: 1;

2) 132 х² – 247 х + 115 = 0.

а + b + с = 132 -247 -115 = 0.

х_{1 =} 1; х₂ = =

Ответ: 1;

Для самостоятельной работы.

Применяя свойства коэффициентов квадратного уравнения, решите уравнения

II. ax² + bx + c = 0, где a ⁰

х_1,2 = . Пусть b = 2k, т.е. чётное. Тогда получим

х_1,2 = = = =

Рассмотрим пример:

3х^{2 –} 14х + 16 = 0 .

D

1 = (-7)² – 3·16 = 49 – 48 = 1

х_{1,2 = ;}

х₁ = = 2; х_{2 =}

Ответ: 2;

Для самостоятельной работы.

а) 4х^{2 –} 36х + 77 = 0

б) 15х^{2 –} 22х – 37 = 0

в) 4х² + 20х + 25 = 0

г) 9х^{2 –} 12х + 4 = 0

Ответы:

а) 3,5; 5,5

б) -1; 2

в) -2,5

г)

III. x² + px + q = 0

х_1,2 = – ± ²– q

Рассмотрим пример:

х² – 14х – 15 = 0

х_1,2 = 7 = 7

х₁ = -1_; х₂ = 15.

Ответ: -1; 15.

Для самостоятельной работы.

а) х² – 8х – 9 = 0

б) х² + 6х – 40 = 0

в) х² + 18х + 81 = 0

г) х² – 56х + 64 = 0

Ответы:

а) -1; 9

б) -10; 4

в) –9

г) 28 18

7. Решение квадратного уравнения с помощью графиков.

Примеры.

а) х² – 3х – 4 = 0

х² = 3х + 4

Ответ: -1; 4

б) х² – 2х + 1 = 0

х² = 3х + 4

Ответ: 1

в) х² – 2х + 5 = 0

х² = 2х -5

Ответ: нет решений

Для самостоятельной работы.

Решить квадратные уравнения графически:

8. Решение квадратных уравнений с помощью циркуля и линейки.

ax² + bx + c = 0,

х² + х + = 0.

х₁ и х₂ – корни.

Пусть А(0; 1), С(0;

По теореме о секущих:

ОВ· ОД = ОА · ОС.

Поэтому имеем:

х₁ · х₂ = 1 · ОС;

ОС = х₁ х₂

К(; 0), где = —

F(0; ) = (0; ) = )

S(-; )

Итак:

1) Построим точку S(-; ) – центр окружности и точку А(0;1).

2) Проведём окружность с радиусом R = SA/

3) Абсциссы точек пересечения этой окружности с осью ох являются корнями исходного квадратного уравнения.

Возможны 3 случая:

1) R > SK (или R > ).

Окружность пересекает ось ох в точке В(х₁; 0) и D(х₂; 0), где х₁ и х₂ – корни квадратного уравнения ax² + bx + c = 0.

2) R = SK (или R = ).

Окружность касается оси ох в тоске В₁(х₁; 0), где х₁ – корень квадратного уравнения

ax² + bx + c = 0.

3) R < SK (или R < ).

Окружность не имеет общих точек с осью ох, т.е. нет решений.

Примеры.

1) x² – 2x – 3 = 0.

Центр S(-; ),т.е.

х₀ = = – = 1,

у₀ = = = – 1.

(1; – 1) – центр окружности.

Проведём окружность (S; AS), где А(0; 1).

 

Ответ: х₁ = – 1; х₂ = 3.

2) x² – 5x + 4 = 0.

х₀ = = – = 2,5; у₀ = = = 2,5.

 

Ответ: х₁ = 1; х₂ = 4.

3) x² + 4x + 4 = 0.

х₀ = = – = – 2,

у₀ = = = 2,5

Ответ: х_{= -2.}

4) x² – 2x + 3 = 0.

х₀ = = – = 1,

у₀ = = = 2.

Ответ: нет решений.

Для самостоятельной работы.

Решить следующие квадратные уравнения с помощью циркуля и линейки:

9. Решение квадратных уравнений с помощью номограммы

Для решения используют Четырёхзначные математические таблицы В.М. Брадиса (таблица XXII, стр. 83).

Номограмма позволяет, не решая квадратного уравнения x² + px + q = 0, по его коэффициентам определить корни уравнения. Например:

5) z² + 4z + 3 = 0.

Оба корня отрицательные. Поэтому сделаем замену: z₁ = – t. Получим новое уравнение:

t² – 4t + 3 = 0.

t₁ = 1 ; t₂ = 3

z₁ = – 1 ; z₂ = – 3.

Ответ: – 3; – 1

6) Если коэффициенты p и q выходят за пределы шкалы, то выполняют подстановку z = k · t и решают с помощью номограммы уравнение: z²+ pz + q = 0.

к² t² + p· kt + q = 0. |: к²

t² + t + = 0.

к берут с расчётом, чтобы имели место неравенства:

Для самостоятельной работы.

С помощью таблицы Брадиса решить следующие квадратные уравнения:

10. Геометрический метод решения квадратных уравнений

Рассмотрим примеры, которые решаются с помощью геометрии.

Пример 1. (из “Алгебры” ал-Хорезми)

х² + 10х = 39.

10 : 4 = 2 ; · 2 = 6 .

S_ABCD = х² + 4S_пр. + 4S_кв. = х² + 4·2х + 4 · 6 = х² + 10х + 25.

Заменим х² + 10х на 39.

S_ABCD = 39 + 25 = 64 = 8².

Значит сторона АВ = 8.

х= 8 – 2 – 2 =8 – 5 = 3.

х = 3

х_{1 +} х₂ = -10,

3 + х₂ = -10,

х₂ = -13.

Ответ: – 13

Пример 2. (решение уравнения древними греками)

у² + 6у – 16 = 0.

у² + 6у = 16, |+ 9

у² + 6у + 9 = 16 + 9

(у + 3)² = 25

у + 3 = ± 5,

у₁ = 2, у₂ = -8.

Ответ: -8; 2

Для самостоятельной работы.

Решите геометрически уравнение у^{2 –} 6у – 16 = 0.

Ответ: – 2; 8.

14.04.2013

xn--i1abbnckbmcl9fb.xn--p1ai

Тренировочные задания на решение квадратных уравнений 8 класс

Квадратные  уравнения 8 класс  алгебра

 

Учитель: Федулкина Т.А.

 

• Что такое квадратные уравнения. Виды уравнений.

Формула квадратного уравнения: ax²+bx+c=0,где a≠0, где x — переменная,  a,b,c — числовые коэффициенты.

 

Пример полного квадратного уравнения:

3x²-3x+2=0
x²-16x+64=0

Решение полных квадратных уравнений сводится к нахождению дискриминанта:

Формула дискриминанта:  D=b²-4aс

Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Если D=0, уравнение имеет один корень 

Если D<0, уравнение не имеет вещественных корней.

№1  x²-x-6=0

Записываем сначала, чему равны числовые коэффициенты a, b и c.

Коэффициент a всегда стоит перед x², коэффициент b  всегда перед переменной x, а коэффициент  c – это свободный член.
a=1,b=-1,c=-6
D=b²-4ac=(-1)²-4∙1∙(-6)=1+24=25

Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

 Ответ: x₁=3; x₂=-2

№2  x²+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
D=b²-4ac=(2)²-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1

Ответ: x=-1

№3 7x²-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
D=b²-4ac=(-1)²-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.

Рассмотрим неполное квадратное уравнение:
ax²+bx=0, где числовой коэффициент c=0.

Пример как выглядят такие уравнения: x²-8x=0, 5x²+4x=0.

Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax²+bx=0  x(ax+b)=0  x₁=0 x₂=-b/a

№1  3x²+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x₁=0      3x+6=0   3x=-6     x₂=-2

Ответ: x₁=0; x₂=-2

№2  x²-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x₁=0
x₂=1

Ответ: x₁=0; x₂=1

Рассмотрим неполное квадратное уравнение:
ax²+c=0, где числовой коэффициент b=0.

Чтобы решить это уравнение, нужно записать так:
x²=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом: корень квадратного уравнения

№1  x²+5=0
x²=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения

№2 3x²-12=0
3x²=12
x²=12/3
x²=4
x₁=2

x₂=-2

Ответ: x₁=2; x₂=-2

 

2) Тренировочные задания на решение квадратных уравнений 8 класс  алгебра.

 

Задания для  устного решения:

 

1. Решите неполное квадратное уравнение:

 

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

2. Решите квадратное уравнение, используя теорему Виета:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

3. Решите квадратное уравнение, используя формулу :

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

4. Найдите дискриминант квадратного уравнения по формуле D= :

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

5. Сколько корней имеет квадратное уравнение, если D= равно:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

3)Решить  квадратные  уравнения:

 

6. Решите квадратное уравнение:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 скачать файл

Дата публикации — 03 декабря 2017

nbschool.edumsko.ru

Урок 8 класс на тему «Квадратные уравнения»

Северо-Казахстанская область

Район Магжана Жумабаева

Полудинская средняя школа

Алгебра 8 класс.

Конспект урока в 8 классе по алгебре

Тема: систематизирующий урок повторения по теме « Квадратные уравнения»

Цель: Закрепить знания и умения учащихся, полученные при изучении темы

Задачи:

Образовательная: уметь применять формулы для нахождения дискриминанта и корней квадратного уравнения; привить навыки устного решения квадратных уравнений.

Развивающая: способствовать развитию логического и творческого мышления, внимания, грамотной математической речи.

Воспитательная: воспитывать такие черты, как память, наблюдательность, самостоятельность, ответственность, дружелюбие.

Тип урока: урок игра КВН – соревнование

Морфологическая карта

Тема урока

Жизненно необходимая информация

Информация, которая встречается в других дисциплинах

Информация, которая нужна для дальнейшего изучения данной дисциплины, ЕНТ

Информация для общего кругозора

Квадратные уравнения

Для решения сложных задач для работающих в области науки.

Физика, экономика, химия

Основополагающая тема по математике в курсе средней школы с 8-11класс

Крупнейший математик XVI в. Франсуа Виет считается создателем буквенного исчисления. Методы решения квадратных уравнений излагаются в древних рукописях Вавилона, в трудах Евклида.

План урока:

1. Организационный момент

2. Викторина

3. Устный счет

4. Работа в группах «Кто быстрее»

5. Работа в группах «Домино»

6. Работа в группах «Теорема Виета»

7. Индивидуальная работа «Гонки «Формула 1»

8. Итог урока.

9. Домашнее задание.

10. Выставление оценок.

ХОД УРОКА

1. Организационный момент.

Создадим хорошее настроение. Улыбнитесь друг другу, садитесь!

Класс разделён на две группы. На доске слова:

Эпиграф урока: «Не решить больших проблем

Без простейших теорем,

И не отыскать сомнений

Без квадратных уравнений»

Умение быстро находить корни имеет большое практическое значение не только в восьмом классе, но и в старших классах, где квадратные уравнения возникают как вспомогательные при решении более сложных задач и где особенно важно, чтобы учащиеся максимально быстро справлялись с решением этих задач.

Сегодня у нас урок закрепление ЗУН, которые вы получили на предыдущих уроках, и мы будем работать с вами по группам (командам), прошу придумать названия ваших команд.

Итак мы начинаем КВН, начнем с разминки. Первым задание у нас будет Викторина. В каждой группе каждому учащемуся я буду задавать вопрос, за правильный ответ вы будете получать фишку. От каждого из вас зависит, сколько ваша группа получит фишек.

1- конкурс

2. Викторина – задание на знание.

Решение квадратных уравнений было вызвано потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием самой математики.

В каком древнем городе ещё около 2000 лет до н.э. первыми научились решать квадратные уравнения? Разгадав кроссворд, мы с вами это узнаем.

1

к

В

а

д

р

а

т

н

о

е

2

д

и

с

к

р

и

м

и

н

А

н

Т

3

д

В

а

4

о

д

И

н

5

н

у

Л

ь

6

н

е

п

О

л

н

о

Е

7

п

р

и

в

е

д

е

Н

н

о

е

1. Как называется уравнение вида ах²+bх+с=0?

2. Название выражения b²-4ас

3. Сколько корней имеет квадратное уравнение, если D >0?

4. Сколько корней имеет квадратное уравнение, если D =0?

5. Чему равен корень уравнения ах²=0?

6. Как называется квадратное уравнение, где коэффициенты

b или с равны нулю?

7. Квадратное уравнение, в котором первый коэффициент, а=1.

3. Следующее задание на понимание — устный счет.

На слайдах вы видите уравнения, для каждой группы отдельный столбик. Каждый из вас в порядке очереди называет ответ, мы проверяем правильность ответа. За правильный ответ группа получает фишку. Начинает та группа, у которой больше фишек.

1— команда 2— команда

уравнения

ответ

уравнения

ответ

1) (x-4)(x+5)=0

2) x(x+7)=0

3) x²+5=0

4) х²-9=0

5) 5х²=0

x₁=4; x₂=-5

x₁=0; x₂=-7

нет корней

x₁=3; x₂=-3

x₁=0; x₂=0

1) (х+2)(х-1)=0

2) х(х-0,3)=0

3) х²+7=0

4) х²-16=0

5) 2,7х²=0

x₁=-2; x₂=1

x₁=0; x₂=0,3

нет корней

x₁=4; x₂=-4

x₁=0; x₂=0

2- конкурс

3. Работа в группах «Кто быстрее».

Каждая команда должна дать ответ как можно быстрее, мы проверяем правильность ответа. За правильный ответ группа получает 3 фишки.

Составьте уравнение для решения задачи. Найти два натуральных числа, если:

3- конкурс

5. Работа в группах «Домино» (анализ)

Собрав домино верно, вы узнаете фамилию математика, который в своей «Арифметике» имел ряд задач, решаемых с помощью составления уравнений разных степеней (на обороте домино написаны буквы), команда которая справиться с этим заданием первые получает 5 фишек.

Диофант — древнегреческий математик, год рождения и дата смерти до сих пор не выяснены. Полагают, что он жил в 3 в. до н.э.

4- конкурс

6. Работа в группах «Теорема Виета»

Ее величество «Теорема Виета»

1. Сформулируйте:

1.Теорему Виета

2. Теорему, обратную теореме Виета.

2.Решите по этой теореме уравнения (3 фишки):

1 команда 2 команда

x² + 9x + 20 = 0; x² + 7x – 60 = 0

5- конкурс

7. Задача про обезьянок

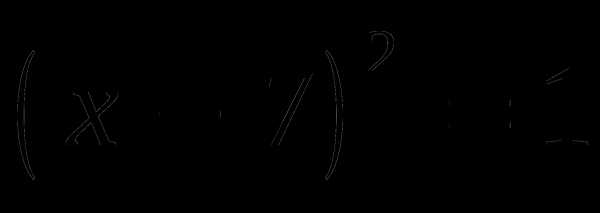
8. Итоги урока.

А теперь подведем итоги. Посчитайте фишки, узнаем, кто больше собрал фишек.

Награждения команды победителей.

9. Рефлексия

Обобщение: Ребята, давайте скажем, что интересного было на нашем уроке, над чем нам дальше необходимо работать, что вам было сложно выполнить, какие трудности встречались (таблица).

8. Домашнее задание:

Повторить главу 2, выполни тест в конце главы «Проверь себя»

10. Выставление оценок (по фишкам).

Урок закончен, все молодцы, спасибо за внимание!

infourok.ru

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Правила комбинаторики в задаче B6
5. Как представить обычную дробь в виде десятичной
6. Задача B15: частный случай при работе с квадратичной функцией

www.berdov.com

«Квадратные уравнения, виды квадратных уравнений»

Алгебра 8 кл Тема: Квадратное уравнение, виды квадратных уравнений.

Цель урока:

• Закрепить умения различать квадратные уравнения, определять коэффициенты квадратного уравнения и по ним определять вид квадратного уравнения. Сформировать умения и навыки решения квадратных уравнений.

• Развивать логическое мышление.

• Воспитывать трудолюбие, развивать самостоятельность.

Ход урока:

Орг. момент.

Актуализация опорных знаний. Проверка д/з.

Устный опрос.

На доске записаны уравнения:

1)х²+ 2х – 8 = 0;

2) 2х² + 5х = 0;

3) 3х² = 0;

4) 2х² + 3х – 8 = 0;

5) х² – 5х + 1 = 0;

6) 6х² + 12 = 0.

Вопросы:

1. Какие уравнения записаны на доске?

2. Какие уравнения называются квадратными?

3. Прочтите полные квадратные уравнения.

4. Какие уравнения называются полными?

5. Как называются уравнения, у которых первый коэффициент равен 1? Приведите примеры.

6. Какое выражение называется дискриминантом?

7. Сколько корней может иметь квадратное уравнение? От чего это зависит?

8. Как называются уравнения под цифрами 2; 3; 6? Почему?

9. Как решаются уравнения под цифрой 2?

10. Чему равенх в уравнении под цифрой 3?

11. Что можно сказать о решении уравнения под цифрой 6?

Проверка домашнего задания.

Проверка в парах. Ученики меняются тетрадями и проверяют задания по готовому решению, оформленному на доске одним из учеников.

Вывод:

Математический диктант

(задания для второго варианта даны в скобках).

Двое решают на разворотах доски:

1. Запишите квадратное уравнение, у которого первый коэффициент равен 3 [- 5], второй коэффициент равен — 5 [3], а свободный член равен 2.
2. Запишите неполное квадратное уравнение, у которого первый коэффициент равен 3 [5], второй – 7 [3], и решите его.
3. Сколько корней имеет это уравнение?

На доске одновременно решаются вторые уравнения.

Решения разбираются. Слабые ученики работают по карточкам.

Работа по карточкам.

Даны уравнения:

3х² – 7х + 4 = 0.

5у² – 6у + 1 = 0;

2у² – 9у + 10 = 0;

у² – 10у – 24 = 0.

Запиши, чему равныа, в, с.

Решить устно № 267.

Закрепление: № 269(неч), 271, 272,273 (неч).

Подведение итогов урока. Д/з. решить №. 269(ч), 271, 272,273 (ч).

Ф.И. _________________________Класс_____ Дата_______

Реши уравнения:

3х² – 7х + 4 = 0. 5у² – 6у + 1 = 0; 2у² – 9у + 10 = 0; .

Ф.И. _________________________Класс_____ Дата_______

Реши уравнения:

3х² – 7х + 4 = 0. 5у² – 6у + 1 = 0; 2у² – 9у + 10 = 0; .

Ф.И. _________________________Класс_____ Дата_______

Реши уравнения:

3х² – 7х + 4 = 0. 5у² – 6у + 1 = 0; 2у² – 9у + 10 = 0; .

infourok.ru

Урок-зачет по теме «Квадратные уравнения» (8-й класс)

Разделы: Математика

---

Форма организации деятельности учителя и учащихся: Урок – общественный смотр знаний

Цели урока:

• обучающие: обобщение и систематизация знаний учащихся по теме “Квадратные уравнения”.
• развивающие: развитие умений преодолевать трудности при решении математических задач; развитие интереса к предмету; расширение кругозора и пополнение словарного запаса; развитие навыков самоконтроля; развитие правильной самооценки.
• воспитательные: воспитание чувства ответственности за порученное дело; воспитание воли и упорства в достижении поставленной цели.

Оборудование:

Интерактивная доска.

Презентация “Квадратные уравнения в Европе”.

На уроке присутствует независимая комиссия, состоящая из учителей, не работающих в классе, которая оценивает ответы учащихся. Общественный смотр знаний является одной из форм контроля знаний, это одна из форм подготовки учащихся к ГИА и ЕГЭ, т.к. некоторые цели смотра совпадают с целями ЕГЭ: проверка знаний независимой комиссией, нестандартная ситуация, разный уровень знаний по сложности, оценка в баллах и перевод их в существующие сейчас отметки. Итоги подводятся по среднему баллу. Вопросы к зачету доводятся до сведения учащихся за две недели. Сообщается, что в ходе урока ученики будут набирать баллы и получат оценку в конце урока. Продолжительность общественного смотра знаний – 90 минут.

Содержание общественного смотра знаний по теме “Квадратные уравнения”.

Теоретические вопросы.

1. Что называется уравнением?
2. Что называется корнем уравнения?
3. Что значит решить уравнение?
4. Какие уравнения называются равносильными?
5. Какие свойства уравнений вы знаете?
6. Какие уравнения называются квадратными?
7. Какие уравнения называются приведенными квадратными уравнениями?
8. Какие уравнения называются неполными квадратными уравнениями? Приведите примеры.
9. Сколько корней имеет квадратное уравнение?
10. Запишите формулу корней квадратного уравнения.
11. Запишите формулу корней квадратного уравнения с четным вторым коэффициентом.
12. Запишите формулу корней приведенного квадратного уравнения с четным вторым коэффициентом.
13. Сформулируйте теорему Виета для приведенного квадратного уравнения.
14. Сформулируйте теорему, обратную теореме Виета.
15. Напишите формулу для разложения квадратного трехчлена на множители.

Ход урока

I. Организационный момент.

1. Проверка готовности учащихся к уроку.
2. Сообщение темы и целей урока.

II. Исторические сведения. Презентация проекта по теме “Квадратные уравнения в Европе. (Приложение).

III. Устный опрос.

1. Что называется уравнением?
2. Что называется корнем уравнения?
3. Что значит решить уравнение?
4. Какие уравнения называются равносильными?
5. Какие свойства уравнений вы знаете?
6. Какие уравнения называются квадратными?
7. Какие уравнения называются приведенными квадратными уравнениями?
8. Какие уравнения называются неполными квадратными уравнениями? Приведите примеры.
9. Сколько корней имеет квадратное уравнение?

IV. Актуализация теоретических знаний.

Учащиеся выполняют задание: Подпишите под таблицей номера правильных, на ваш взгляд, ответов. (Кодированные вопросы.)

Вопросы	Ответы
	1	2	3
1. В каком случае уравнение ах2 + вх + с = 0 называется квадратным?	в ≠ 0 с ≠ 0 а = 0	а ≠ 0	а = 1
2. Как называются уравнения ах2 = 0; ах2 + вх = 0; ах2 + с = 0?	Приведенные квадратные уравнения	Неполные квадратные уравнения	Полные квадратные уравнения
3. Сколько корней имеет квадратное уравнение ах2 = 0?	Два корня	Нет корней	Один корень
4. Сколько корней имеет уравнение ах2 + вх = 0?	Два корня	Нет корней	Один корень
5.Сколько корней имеет уравнение ах2 + с = 0, если а и с имеют одинаковые знаки?	Два корня	Нет корней	Один корень
51. Сколько корней имеет уравнение ах2 + с = 0, если а и с имеют разные знаки?	Два корня	Нет корней	Один корень
6. Уравнение ах2 + вх + с = 0 имеет два корня, если	D<0	D>0	D=0
61. Уравнение ах2 + вх + с = 0 имеет два корня, если	D<0	D>0	D=0
62.Уравнение ах2 + вх + с = 0 имеет два корня, если	D<0	D>0	D=0
7. Является ли равенство х1,2= формулой корней квадратного уравнения ах2 + вх + с = 0?	Нет	Да	Не знаю
8. Теорема Виета для уравнения х2 + рх + q = 0	х1 + х2 = -q х1·х2 = р	х1 + х2 = q х1·х2 = р	х1+ х2 = -р х1·х2 = q

V. Устный опрос.

Решите устно уравнения, предварительно произведя их классификацию:

16х^{2 –} 25 = 0; -12 + х² = 0; 2х² + х = 0; 4х² + 4х + 1 = 0; х² – 6х – 16 = 0; 9х²  – 16 = 0; -х² + 18 = 0;

5х² + х = 0; 1– 6х + 9х² = 0; х² – 10х – 24 = 0.

Найдите общий корень уравнения и постарайтесь объяснить результат:

1) а) х² – 5х + 4 = 0; б) х² + 8х – 9 = 0; в) 4х² – 3х – 1 = 0.

2) а) х² + 5х + 4 = 0; б) х² – 8х – 9 = 0; в) 4х² + 3х – 1 = 0.

V. Решение заданий по вариантам

Задание № 1.

I-й вариант.

Классифицируйте уравнения и решите их наиболее рациональным способом:

4х² + х = 0; 16 – х² = 0; 2х² + х – 1 = 0; 5х² + 14х – 3 = 0; х² – 4х + 3 = 0; х² – 2010х + 2009 = 0

Полные квадратные уравнения	Неполные квадратные уравнения	Приведенные квадратные уравнения, решаемые с помощью теоремы Виета	Квадратные уравнения с четным вторым коэффициентом

II-й вариант.

Классифицируйте уравнения и решите их наиболее рациональным способом:

3х² + х = 0; 4 – х² = 0; 3х² – х – 2 = 0; 5х² + 8х – 4 = 0; х² – 6х + 5 = 0; х² – 2009х + 2008 = 0

Полные квадратные уравнения	Неполные квадратные уравнения	Приведенные квадратные уравнения, решаемые с помощью теоремы Виета	Квадратные уравнения с четным вторым коэффициентом

Задание № 2.

I-й вариант.

1. Решите уравнение:

(3х – 1)(х + 3) + 1 = х(1 + 6х)

2. Найдите подбором корни уравнения: х² + 20х + 36 = 0.

3. При каких значениях m уравнение 4х² + 2х – m = 0 имеет единственный корень?

II-й вариант.

1. Решите уравнение:

(х + 4)(2х – 1) = х(3х + 11).

2.Найдите подбором корни уравнения: х² + 14х + 24 = 0.

3. При каких значениях с уравнение 3х² – 4х + с = 0 имеет единственный корень?

Устно разложите квадратный трехчлен на множители:

х² – х – 30; х² + х – 42; х² – 6х + 8; х² + 8х + 15.

Задание № 3.

I-й вариант.

1. Какой из данных многочленов является квадратным трехчленом?

8х2 + 4 – х3

4х – 9 + 2х2

2х4 – 5х2 + 1

х2 + х6 – 2

2. Разложите на множители квадратные трехчлены:

5х2 – 3х – 2 =

3х2 + 5х + 2 =

3. Сократите дробь: а) ; б).

II-й вариант.

1. Какой из данных многочленов является квадратным трехчленом?

4 – 9х + 3х2

7х2 – 4х – х3

х2 – 5х4 + 2

2х8 + 5х6 – 2

2. Разложите на множители квадратные трехчлены:

2х2 + 7х – 4 =

3х2 + 8х – 3 =

3. Сократите дробь: а); б).

VI. Решение задач.

Записать на доске уравнение по условию задачи (дополнительное задание):

• Одно из двух натуральных чисел больше другого на 5. Найдите эти числа, если их произведение равно 24.
• Найдите число, которое на 12 меньше его квадрата.
• Площадь прямоугольной пластины равна 120 см². Найдите длину и ширину пластины. Если известно, что длина на 2 см больше ширины.

Решите самостоятельно:

Задание № 4.

I-й вариант.

Решите задачу:

1. В прямоугольном треугольнике один из катетов на 7 см больше другого. Найдите периметр треугольника, если его гипотенуза равна 13 см.
2. Один из корней данного уравнения в 2 раза больше другого. Найдите корни уравнения и коэффициент к: 2х²-3х+к=0.
3. Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 ч. Какова скорость течения реки?

II-й вариант.

Решите задачу:

1. Одна из сторон прямоугольника на 2см меньше другой, а его диагональ равна 10 см. Найдите периметр прямоугольника.
2. Один из корней данного уравнения в 2 раза больше другого. Найдите корни уравнения и коэффициент к: 2х²—кх+4 =0.
3. Катер прошел 40 км по течению реки и 6 км против течения, затратив на весь путь 3ч. Какова собственная скорость катера, если скорость течения 2 км/ч?

VIII. Домашнее задание.

Оценочный лист учащихся 8А класса.

Общественный смотр знаний по теме “Квадратные уравнения”.

Фамилия, имя	Устные задания	Кодированные ответы	Задание №1	Задание №2	Задание №3	Задание №4	Дополнительное задание	Рейтинг	Оценка

За каждый устный ответ ставится 0,5 балла

Максимальное количество баллов за задание “Кодированные вопросы” – 2 балла

Максимальное количество баллов за задание № 1 – 6 баллов

Максимальное количество баллов за задание № 2 – 6 баллов

Максимальное количество баллов за задание № 3 – 6 баллов

Максимальное количество баллов за задание № 4 – 6 баллов

Максимальное количество баллов за дополнительное задание – 6 баллов

Система оценивания результатов урока

Рейтинг	0–6 баллов	7– 10 баллов	11–15 баллов	16 и более баллов
Оценка	2	3	4	5

8.07.2010

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Урок математики по теме: «Квадратные уравнения» (8 класс)

ГУ «Актюбинская основная школа»

Открытый урок по теме:

8-класс

Учитель математики: Нагашбаева З.С.

2010-2011 учебный год

Тема урока: Квадратные уравнения.

Эпиграф к уроку: «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным».

 

Паскаль

Цели:

1. Показать уровень усвоения программного материала по теме «Квадратные уравнения», навыки решения квадратных уравнений с помощью применения формул корней квадратных уравнений, изучить новый способ решения квадратных уравнений.

2. Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического мышления,

3. Способствовать рациональной организации труда, внимательность, активное участие в учебно-познавательном процессе, самостоятельность, самокритичность.

Оборудование к уроку: тест «Квадратные уравнения», интерактивная доска, таблицы, карточки.

 

 

План урока

1. Организационный момент «Настроимся на урок!»

2. Проверка домашнего задания

3. Тест «Квадратные уравнения».

4. Работа в парах: математика и биология.

5. Немного истории.

6. Продвинутые способы решения квадратных уравнений

7. Викторина «Дальше, дальше…»

8. Итог.

 

 

Ход урока

 

1. Организационный момент «Настроимся на урок!»

Здравствуйте, ребята и гости нашего урока! Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики — любознательность. Постараемся доказать это на уроке. Мы с вами начали изучать новый большой раздел «Квадратные уравнения», на который отводится 20 уроков.

Сегодня четвертый урок из этой главы, однако, вы уже умеете решать квадратные уравнения. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.

Эпиграфом к уроку я взяла слова великого математика Паскаля «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным». В течение урока мы еще вернемся к этим словам.

 

2. Проверка домашнего задания

Начнем урок с проверки домашнего задания.

Правильность решения заданий вы не сможете проверить, т.к. на предыдущем уроке каждый получил индивидуальное задание в зависимости от способностей и возможностей.

А вот знание теоретического материала, который понадобится нам на протяжении всего урока, давайте вспомним.

Какой вид имеет квадратное уравнение?

Какие уравнения вы знаете? (полные и неполные)

Сколько решений имеет полное квадратное уравнение? От чего это зависит?

3. Тест «Квадратные уравнения».

Итак, мы повторили, как можно решить квадратное уравнение. Сейчас я хотела бы проверить, как вы усвоили эти формулы и определения.

Ученики получают карточки с заданиями. Заполняют пропущенные слова в карточках.

 

I ВАРИАНТ

1. Уравнение вида , где a, b, c — заданные числа, a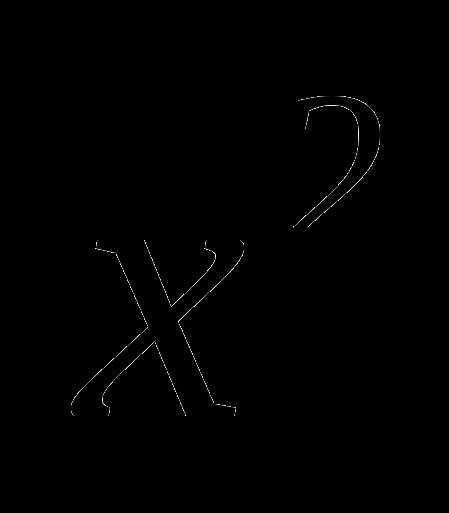0, x — переменная, называется…

2. Полное квадратное уравнение не имеет корней, если D …

3. Уравнение вида называется…

4. Квадратное уравнение имеет два корня, если…

5. Дано уравнение . D =…

 

II ВАРИАНТ

1. Если квадратное уравнение, то a… коэффициент, с…

2. Уравнение x² = a, где a < 0, не имеет…

3. Полное квадратное уравнение имеет единственный корень, если …

4. Уравнение вида ax² + c = 0, где a 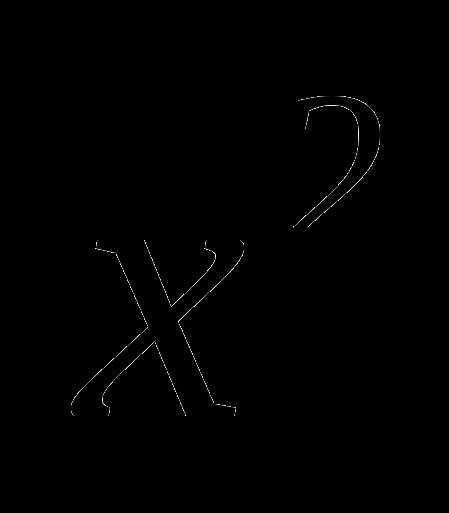0, c 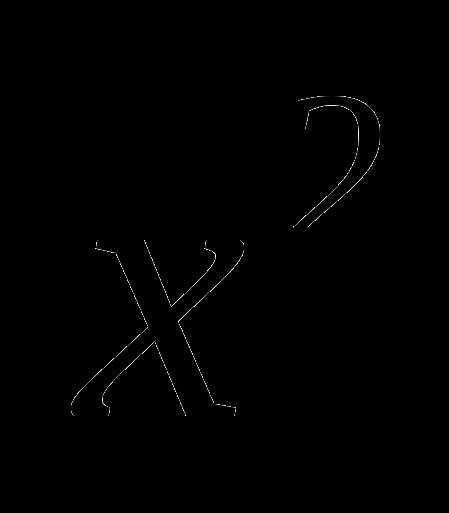0, называют … квадратным уравнением.

5. Дано уравнение x²- 6x + 8 = 0. D =…

Проводится взаимопроверка. Ответы показываем через интерактивную доску.

4. Работа в парах

 Вернемся к эпиграфу нашего урока. Попытаемся сделать математику хотя бы сегодня на уроке немного более занимательной.

Вам необходимо угадать, что же находится в черном ящике.

Математика и биология

Учитель: Угадайте, что в ящике. Даю три определения этому предмету:

1. Непроизводная основа слова.

2. Число, которое после постановки его в уравнение обращает уравнение в тождество.

3. Один из основных органов растений.

/Корень/

 

Учитель: Вы должны определить, какого растения это корень, решив следующие уравнения в парах.

1. x²- 8x + 15 = 0

2. x² — 11x + 18 = 0

3. x² — 5x — 6 = 0

4. x² — 4x + 4 = 0

5. 3x² + 4x + 20 = 0

6. 5x²- 3x — 2 = 0

 

Учитель: Игра «Математическое лото». Найдите полученный ответ на экране. Проверить результат. Если ученики получают правильный ответ, то получат изображение розы, иначе – слайд с текстом «Проверьте решение».

 

Учитель: Что это за растение?

 

Ответ: Роза.

 

Учитель: Значит, в черном ящике лежал корень розы, о которой в народе говорят: «Цветы ангельские, а когти дьявольские». О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.

 Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Мы увидели, что слово «корень» встречается на уроках биологии и математики. И не только.

 

4. Немного истории.

По словам математика Лейбница, «кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».

Ученик заранее готовит сообщение об истории квадратных уравнений, с презентацией.

 6. Продвинутые способы решения квадратных уравнений

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.

В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. В математической науке есть десять способов решения квадратных уравнений.

Способы решения квадратных уравнений, изучаемые в школе:

• Разложение левой части на множители

• Метод выделения полного квадрата

• С применением формул корней квадратного уравнения

• С применением теоремы Виета

• Графический способ

Продвинутые способы решения квадратных уравнений:

• Способ переброски

• По свойству коэффициентов

• С помощью циркуля и линейки

• С помощью номограммы

• Геометрический

Сегодня на уроке мы познакомимся с новым способом решения квадратных уравнений, который не изучается в школе. Но он очень интересный и вовсе не сложный.

Решение квадратных уравнений по свойству коэффициентов.

Пусть дано квадратное уравнение

ах² + bх + с = 0, где а ≠0.

Свойство 1.

Если а + b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х₁ = 1, х₂ = с/а

Свойство 2.

Если а – b + с = 0, или b = а + с, то

х₁ = – 1, х₂ = – с/а

Пример:

Решите самостоятельно:

1 вариант: 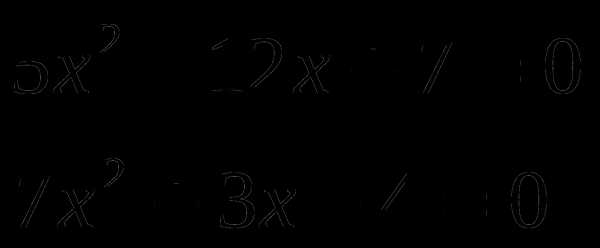2 вариант: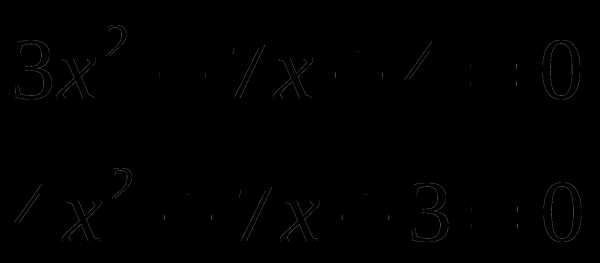

7. Викторина. «Дальше, дальше…»

В течение одной минуты ребята отвечают на вопросы, приведенные ниже:

1. Уравнение второй степени.

2. Сколько корней имеет квадратное уравнение, если D больше 0?

3. Равенство с переменной?

4. От чего зависит количество корней квадратного уравнения?

5. Как называется квадратное уравнение, у которого первый коэффициент — 1?

6. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?

7. Что значит решить уравнение?

8. Есть у любого слова, у растения и может быть у уравнения?

7. Итог урока.

Учитель:

Что нового мы узнали на уроке?

Какое уравнение называется квадратным?

Какие виды квадратных уравнений вы знаете?

И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

Оценивание учащихся. Сообщение домашнего задания.

infourok.ru