3. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма.
Известно два способа задания логических функций: с помощью формулы и с помощью таблицы истинности. По формуле легко составляется таблица. На практике при конструировании различных электронных устройств часто возникает обратная задача – от таблицы истинности перейти к формуле, чтобы на ее основе построить функциональную схему.
Введем следующие определения:
Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ).
Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ).
Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
Приведем примеры формул, соответствующих и не соответствующих этим определениям:
НАЗВАНИЕ ФОРМУЛЫ В ОПРЕДЕЛЕНИИ | Формула, соответствующая определению | ФОРМУЛА, НЕ СООТВЕТСТВУЮЩАЯ ОПРЕДЕЛЕНИЮ |
Элементарная дизъюнкция | | |
Элементарная конъюнкция | | |
ДНФ | 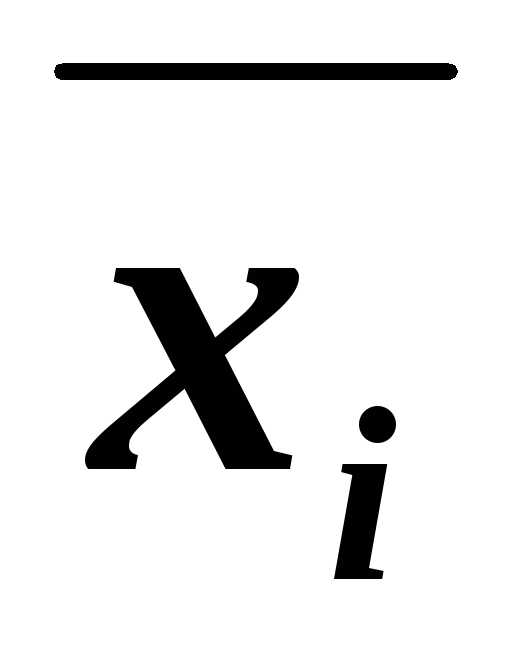 | ДНФ можно построить для всякой формулы (путем преобразования) |
КНФ | КНФ можно построить для всякой формулы (путем преобразования) | |
СДНФ | ||
СКНФ |
Любую функцию, кроме констант 0 и 1, можно представить в виде как СДНФ, так и СКНФ.
Этот факт является теоремой алгебры логики. Из него следует, что любая формула (кроме констант 0 и 1) может быть преобразован к виду как СДНФ, так и СКНФ. Константа 0 может быть представлена только СКНФ (), а константа 1 – только СДНФ (). Из вышесказанного следует, что если надо построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.
Алгоритм получения СДНФ по таблице истинности:
Отметить те строчки таблицы истинности, в последнем столбце которых стоят 1:
X
Y
F(X,Y)
0
0
0
1
1*
1
0
1*
1
1
0
Выписать для каждой отмеченной строки конъюнкциювсех переменных следующим образом: если значение некоторой переменной в данной строкеравно 1, то в конъюнкцию включатьсаму эту переменную, еслиравно 0, то ееотрицание:
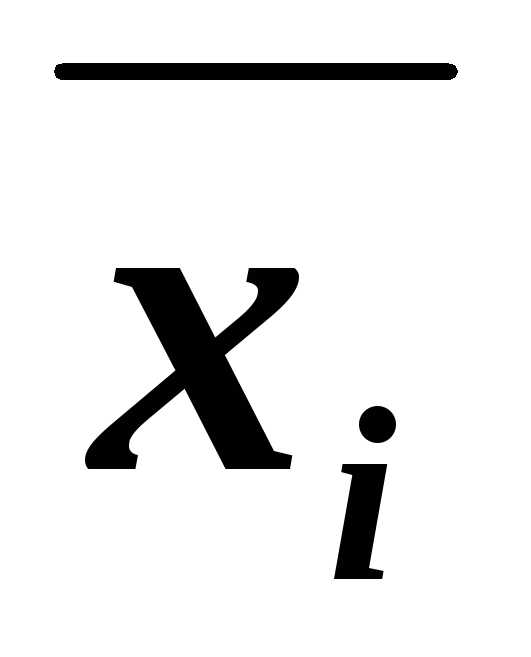
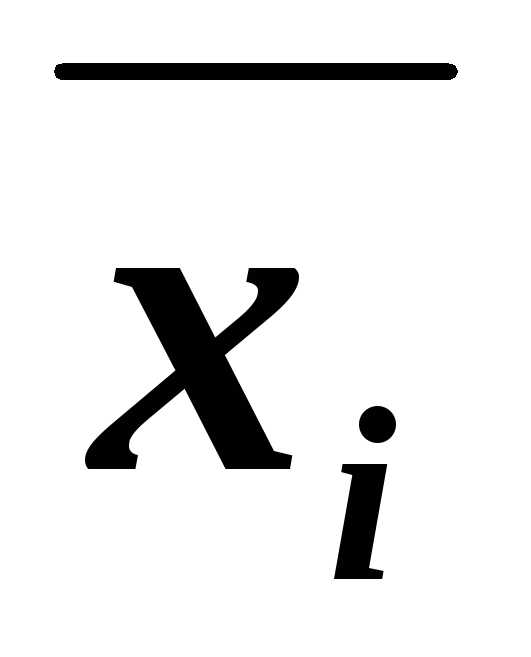 – для 3-й строки.
– для 3-й строки.
Все полученные конъюнкции связать в дизъюнкцию: .
Алгоритм получения СКНФ по таблице истинности:
Отметить те строки таблицы истинности, в последнем столбце которых стоит 0:
X
Y
F(X,Y)
0
0
0*
01
1
1
0
1
1
1
0*
Выписать для каждой отмеченной строки дизъюнкциювсех переменных следующим образом: если значение некоторой переменной в данной строкеравно 0, то в дизъюнкцию включатьсаму эту переменную, еслиравно 1, то ееотрицание:
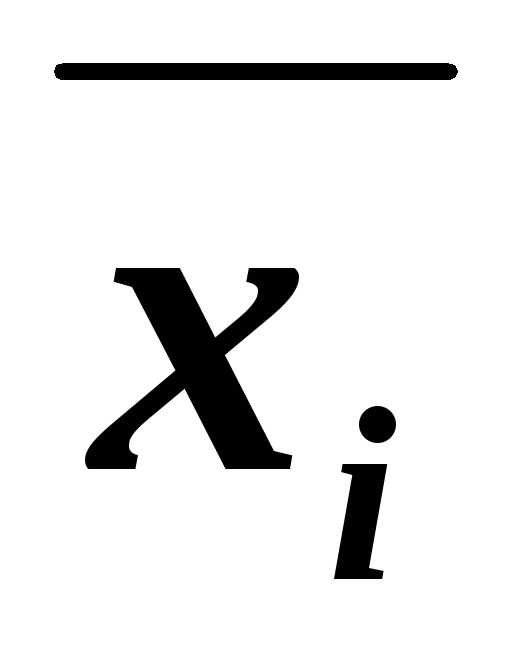 – для 1-й строки;
– для 1-й строки;
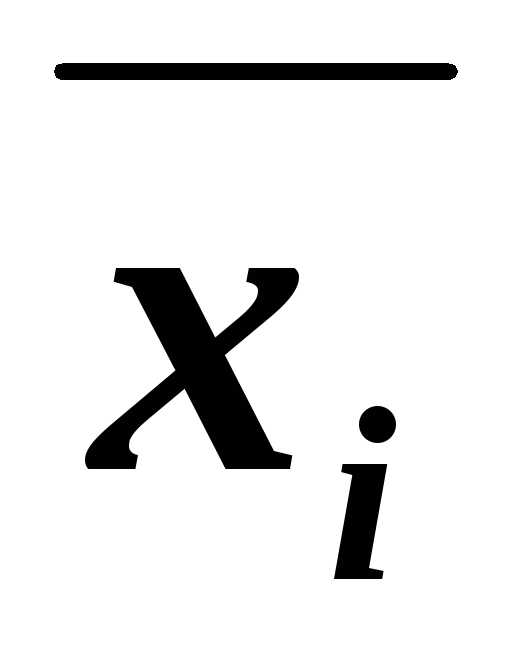 – для 4-й строки.
– для 4-й строки.
Все полученные дизъюнкции связать в конъюнкцию: .
Покажем, что полученные по двум алгоритмам СДНФ и СКНФ эквивалентны. Преобразуем СКНФ по правилам алгебры логики: .
Примечание: для нахождения формулы по таблице истинности рекомендуется использовать тот из двух алгоритмов, в котором в таблице помечается меньше строк.
ТИПОВЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА ЭВМ.
К типовым логическим устройствам ЭВМ относятся сумматоры, полусумматоры, триггеры, счетчики, регистры, шифраторы, дешифраторы.
СУММАТОРЫ.
Сумматор является основным узлом арифметико-логического устройства ЭВМ и служит для суммирования чисел посредством поразрядного сложения.
Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. При этом если сумма двух цифр в данном разряде больше или равна основанию используемой системы счисления, то возникает перенос старшего разряда в соседний сумматор.
Одноразрядный сумматор должен иметь два выхода: для суммы и для переносимого значения. У него может быть два или три (для складываемых значений и значения переноса) входа.
Одноразрядный двоичный сумматор на два входа и два выхода называется одноразрядным полусумматором.
Одноразрядный двоичный сумматор на три входа и два выхода называется одноразрядным сумматором на три входа.
studfiles.net
2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций
Определение 1. Конъюнктивным одночленом (элементарной конъюнкцией) от переменных называется конъюнкция этих переменных или их отрицаний.
Например, – элементарная конъюнкция.
Определение 2. Дизъюнктивным одночленом (элементарной дизъюнкцией) от переменных называется дизъюнкция этих переменных или их отрицаний.
Например, – элементарнаядизъюнкция.
Определение 3. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.
Например, – ДНФ.
Определение 4. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется
Например, – КНФ.
Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.
Алгоритм построения нормальных форм
С помощью равносильностей алгебры логики заменить все имеющиеся в формуле операции основными: конъюнкцией, дизъюнкцией, отрицанием:
;
;
.
Заменить знак отрицания, относящийся к выражениям типа или, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
; .
Избавиться от знаков двойного отрицания.
Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Определение 1. Совершенная дизъюнктивная нормальная форма (СДНФ) – это ДНФ, в которой в каждый конъюнктивный одночлен каждая переменная из наборавходит ровно один раз, причем входит либо сама, либо ее отрицание.
Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, можно определить следующим образом:
Определение 2. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы алгебры высказываний называется ее ДНФ, обладающая следующими свойствами:
ДНФ не содержит двух одинаковых конъюнкций;
ни одна конъюнкция не содержит одновременно двух одинаковых переменных;
ни одна конъюнкция не содержит одновременно некоторую переменную и ее отрицание;
каждая конъюнкция содержит либо переменную , либо ее отрицаниедля всех переменных, входящих в формулу.
Определение 3. Совершенная конъюнктивная нормальная форма (СКНФ) – это КНФ, в которой в каждый дизъюнктивный одночлен каждая переменная из наборавходит ровно один раз, причем входит либо сама, либо ее отрицание.
Конструктивно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить следующим образом.
Определение 4. Совершенной конъюнктивной нормальной формой (СКНФ) данной формулы алгебры высказываний называется такая ее КНФ, которая удовлетворяет следующим свойствам.
КНФ не содержит двух одинаковых дизъюнкций.
Ни одна конъюнкция не содержит одновременно двух одинаковых переменных.
Ни одна из дизъюнкций не содержит одновременно некоторую переменную и ее отрицание.
Каждая дизъюнкция СКНФ содержит либо переменную , либо ее отрицаниедля всех переменных, входящих в формулу.
Теорема 1. Каждая булева функция от переменных, не являющаяся тождественно ложной, может быть представлена в СДНФ, и притом единственным образом.
Способы нахождения СДНФ
1-й способ – с помощью равносильных преобразований:
получаем одну из ДНФ;
если в полученной ДНФ входящая в нее элементарная конъюнкция не содержит переменную, то используем равносильностьи получаем две элементарных конъюнкции;
если в ДНФ входят две элементарные конъюнкции, то лишнюю можно отбросить.
2-й способ – с помощью таблиц истинности:
выделяем строки, где формула принимает значение 1;
составляем дизъюнкцию конъюнкций при условии, что если переменная входит в конъюнкцию со значением 1, то записываем эту переменную, если со значением 0, то ее отрицание. Получаем СДНФ.
Теорема 2. Каждая булева функция от переменных, не являющаяся тождественно истинной, может быть представлена в СКНФ, и притом единственным образом.
Способы нахождения СКНФ
1-й способ – с помощью равносильных преобразований:
получаем одну из КНФ;
если в полученной КНФ входящая в нее элементарная дизъюнкция не содержит переменную, то используем равносильностьи получаем две элементарных дизъюнкции;
если в КНФ входят две элементарные дизъюнкции, то лишнюю можно отбросить.
2-й способ – с помощью таблиц истинности:
выделяем строки, где формула принимает значение 0;
составляем конъюнкцию дизъюнкций при условии, что если переменная входит в дизъюнкцию со значением 0, то записываем эту переменную, если со значением 1, то ее отрицание. Получаем СКНФ.
Пример 1. Постройте КНФ функции .
Решение
Исключим связку «» с помощью законов преобразования переменных:
= /законы де Моргана и двойного отрицания/ =
/дистрибутивные законы/ =
.
Пример 2. Приведите к ДНФ формулу .
Решение
Выразим логические операции ичерез,и:
= /отнесем отрицание к переменным и сократим двойные отрицания/ =
= /закон дистрибутивности/ .
Пример 3. Запишите формулу в ДНФ и СДНФ.
Решение
Используя законы логики, приведем данную формулу к виду, содержащему только дизъюнкции элементарных конъюнкций. Полученная формула и будет искомой ДНФ:
Для построения СДНФ составим таблицу истинности для данной формулы:
0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 0 0 0 0 0 1 1 | 0 1 0 1 0 1 1 1 | 1 0 1 0 1 0 0 0 |
Помечаем те строки таблицы, в которых формула (последний столбец) принимает значение 1. Для каждой такой строки выпишем формулу, истинную на наборе переменных ,,данной строки:
строка 1: ;
строка 3: ;
строка 5: .
Дизъюнкция этих трех формул будет принимать значение 1 только на наборах переменных в строках 1, 3, 5, а следовательно, и будет искомой совершенной дизъюнктивной нормальной формой (СДНФ):
.
Пример 4. Приведите формулу к СКНФ двумя способами:
а) с помощью равносильных преобразований;
б) с помощью таблицы истинности.
Решение:
a)
Преобразуем вторую элементарную дизъюнкцию:
.
Формула имеет вид:
б) составим таблицу истинности для данной формулы:
1 1 1 1 0 0 0 0 | 1 1 0 0 1 1 0 0 | 1 0 1 0 1 0 1 0 | 0 1 0 1 0 1 0 1 | 1 1 1 1 0 1 0 1 | 1 0 1 1 1 0 1 1 | 1 0 1 1 1 0 1 1 |
Помечаем те строки таблицы, в которых формула (последний столбец) принимает значение 0. Для каждой такой строки выпишем формулу, истинную на наборе переменных ,,данной строки:
строка 2: ;
строка 6: .
Конъюнкция этих двух формул будет принимать значение 0 только на наборах переменных в строках 2 и 6, а следовательно, и будет искомой совершенной конъюнктивной нормальной формой (СКНФ):
.
Вопросы и задачи для самостоятельного решения
1. С помощью равносильных преобразований приведите к ДНФ формулы:
а) ;
б) ;
в) .
2. С помощью равносильных преобразований приведите к КНФ формулы:
а) ;
б) ;
в) .
3. С помощью второго дистрибутивного закона преобразуйте ДНФ в КНФ:
а) ;
б) .
4. Преобразуйте заданные ДНФ в СДНФ:
а) ;
б) ;
в) .
5. Преобразуйте заданные КНФ в СКНФ:
а) ;
б) ;
в) .
6. Для заданных логических формул постройте СДНФ и СКНФ двумя способами: с помощью равносильных преобразований и с помощью таблицы истинности.
а) ;
б) ;
в).
studfiles.net
4.2. Конъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.
Определение 5. Дизъюнкция
(4.2)
называется элементарной дизъюнкцией или дизъюнктом.
Как и в случае конъюнктов, существует 2n различных элементарных дизюъюнкций от n переменных. При этом значение элементарной дизюъюнкции вида (4.2) равно 0 тогда и только тогда, когда xi=1i для всех i=1, 2, …, n.
Конъюнкция вида (4.1) называется также конституентой нуля.
Определение 6. Конъюнктивной нормальной формой формулы А (КНФА) называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Пример 4.2. Для
формулы А=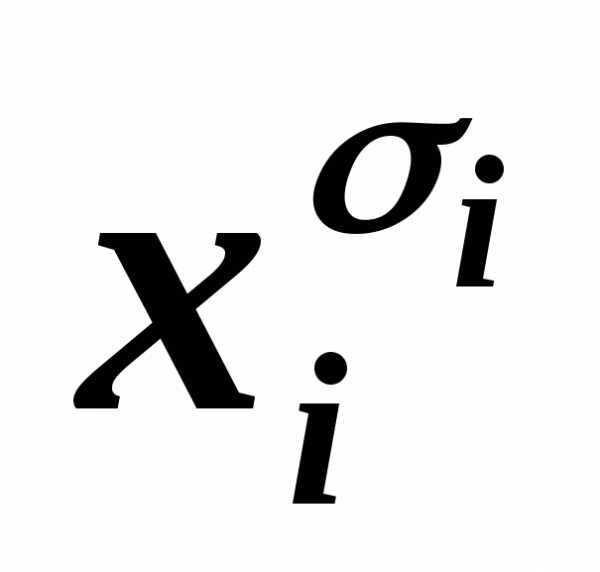 (
(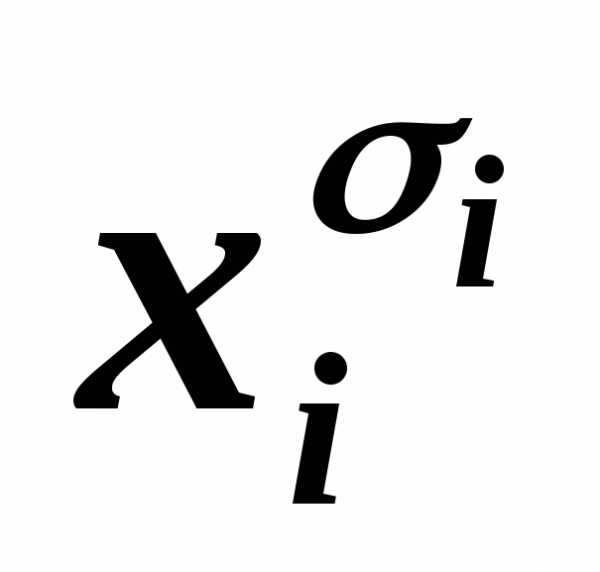 у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.
Как и в случае ДНФ, КНФ формулы неединствен. Их можно составить сколько угодно. К КНФ формулы можно прийти по следующему алгоритму:
I шаг: Приведение операций |, , , , к операциям &, или их отрицаниям:
1. Если в формуле участвуют операции |, , и , то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций.
2. Если в формуле участвует операция , то от неё с помощью закона т) упражнения 3.2 переходим к операции .
3. Если в формуле участвует операция , то от неё с помощью закона п) упражнения 3.2 преходим к операции .
II шаг. Отнесение отрицаний к пропозициональным переменным.
4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным.
5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются.
III шаг. Получение КНФ.
С помощью свойства дистрибутивности относительно & все подформулы вида A(B1&B2&…&Bk) приводим к подформулам вида (AB1)&(AB2)&…&(ABk) до тех пор, пока не получим конъюнкцию элементарных дизъюнкций.
Таким образом, мы доказали, что любая формула эквивалентна некоторой КНФ.
Очевидно, А&А&…&А~А, и поэтому в КНФ элементарная дизъюнкция может повторяться сколько угодно раз. В результате мы приходим к тому, КНФ формулы можно построить сколько угодно.
Потребуем, чтобы КНФ удовлетворяла следующим четырём свойствам совершенства:
1. Каждый дизъюнкт КНФ формулы содержит все переменные или их отрицания, входящие в формулу.
2. Все дизъюнкты, входящие в КНФ, различны.
3. Ни один дизъюнкт, из которых состоит КНФ, не содержит одновременно переменную и её отрицание.
4. Ни один дизъюнкт не содержит одну же литеру два и более раз.
Определение 7. КНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной конъюнктивной нормальной формой данной формулы (СКНФ).
Для того, чтобы получить СКНФ формулы А, достаточно сначала формулу привести к КНФА, а затем применить к полученной КНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную КНФА, удовлетворяющие всем условиям совершенства:
1. Если в КНФА какой-либо дизъюнкт В не содержит переменную хi или её отрицание, то используя
равносильности B~В(хi&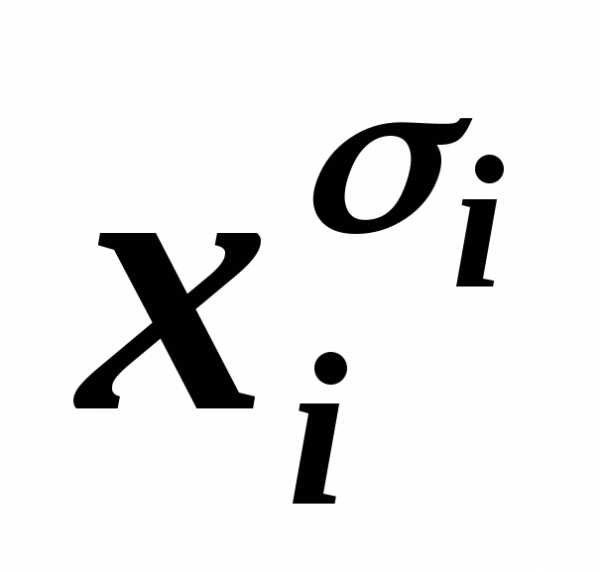 )~
~(Вхi)&(B
)~
~(Вхi)&(B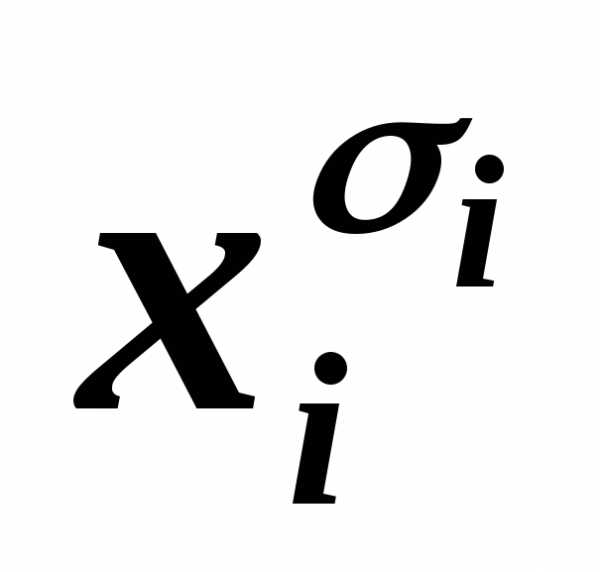 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B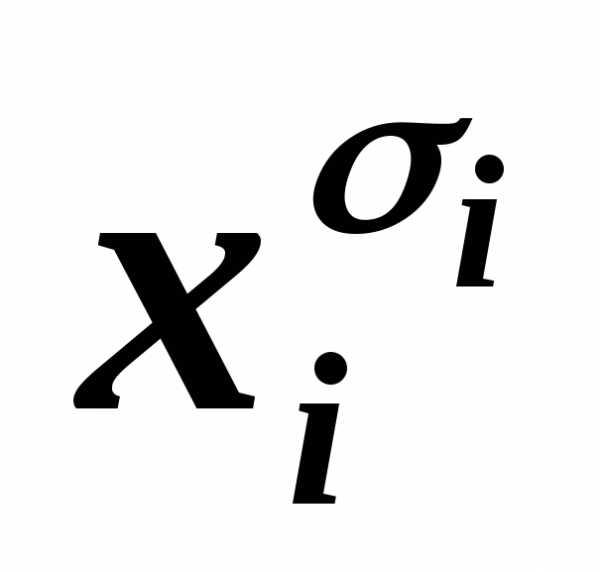 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание  .
.
2. Если в КНФА входят два или более одинаковых дизъюнкта B, то лишние отбрасываем, пользуясь равносильностью B&B&…&B~B.
3. Если некоторый
дизъюнкт В,
входящий в КНФА,
содержит переменную хi и её отрицание 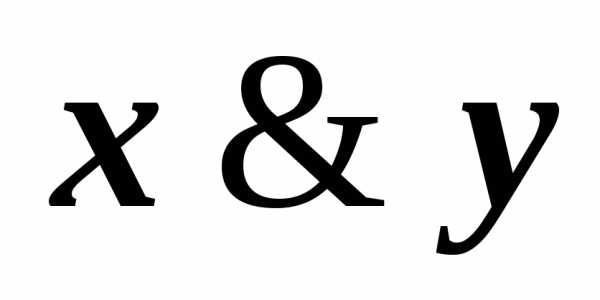 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
4. Если некоторый
дизъюнкт, входящий в КНФА,
содержит одну и ту же литеру  дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью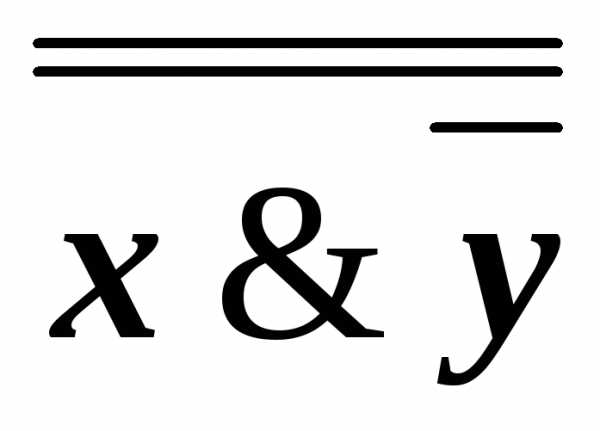
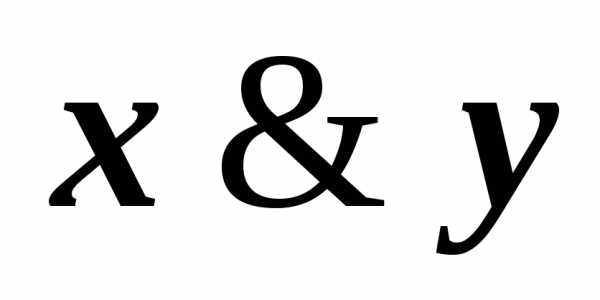 …
… ~
~ ,
лишние отбрасываем.
,
лишние отбрасываем.
Упражнение 4.3.С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СКНФ.
Решение. з) Приведём формулу к КНФ:
(x| )(z
)(z )
) (
( )(z
)(z )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x&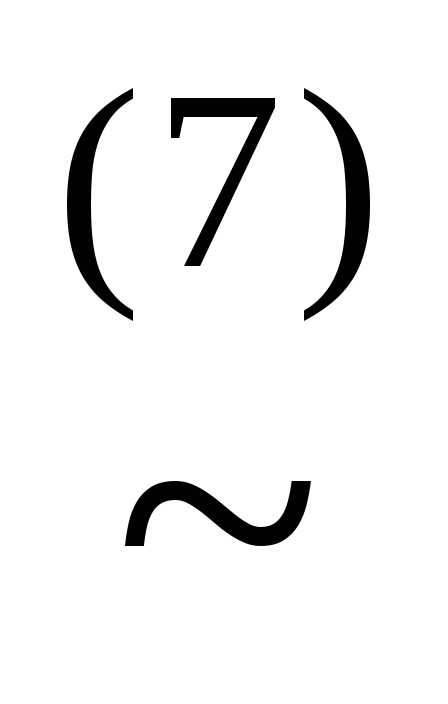 )
)
 (x&
(x& )
)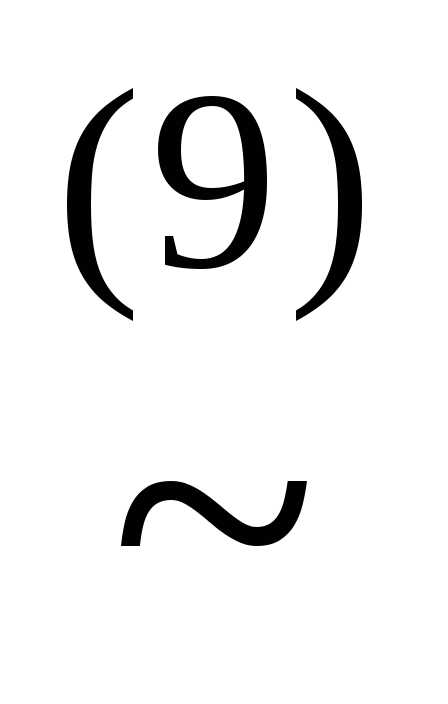 (x&
(x& )
)
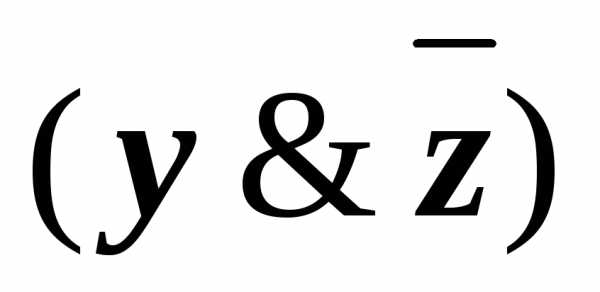 (x&
(x&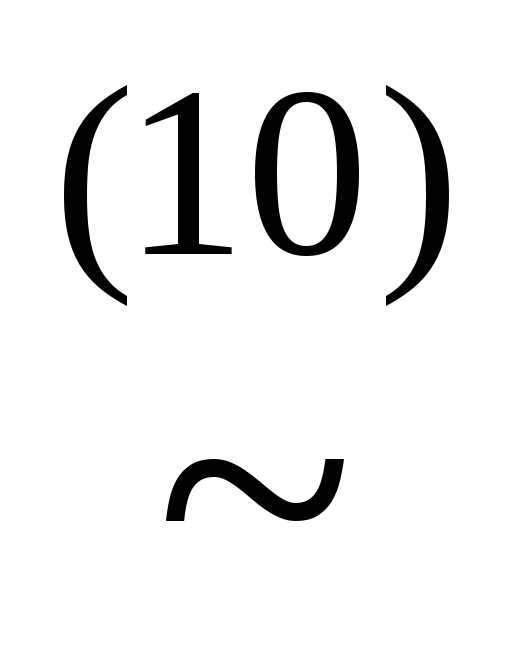 )(
)( (x&
(x&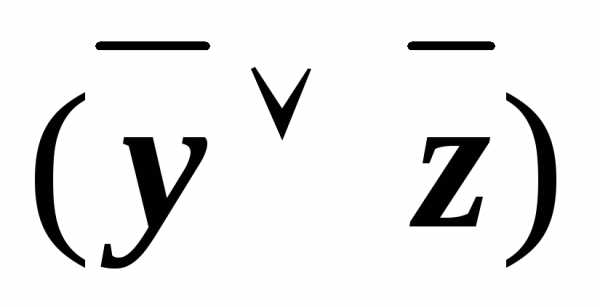 ))
))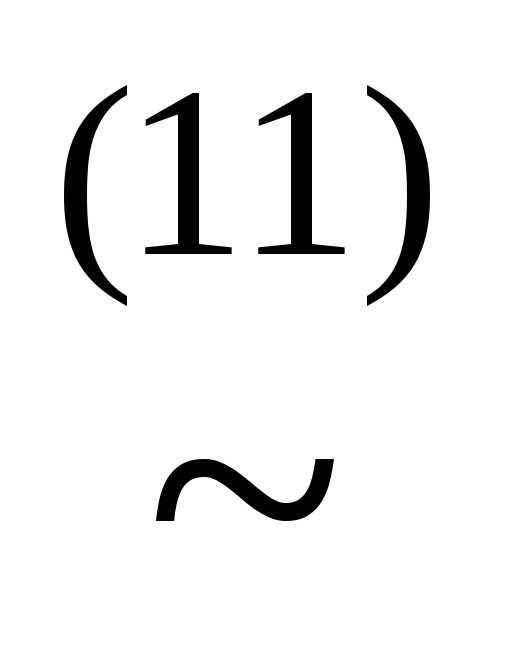
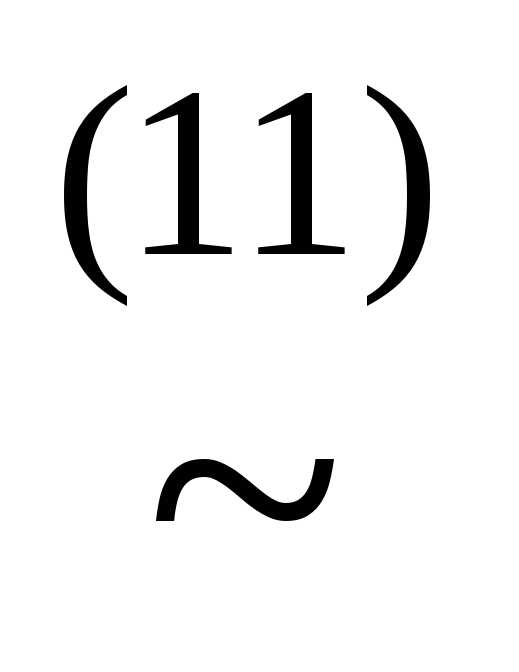 (x&(
(x&(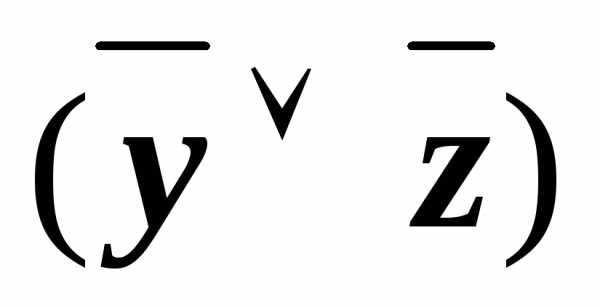
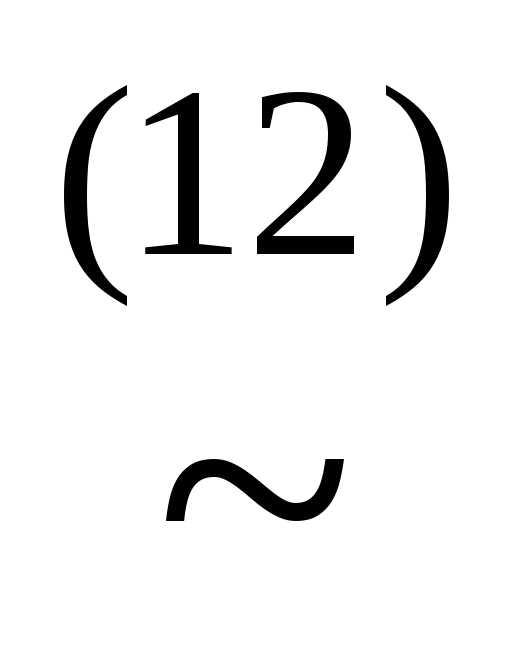 )))
))) (x&((
(x&(( у)&
у)&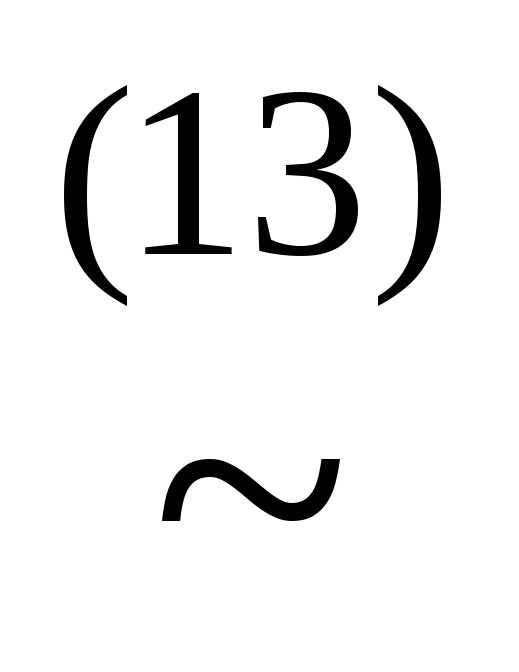 )))
)))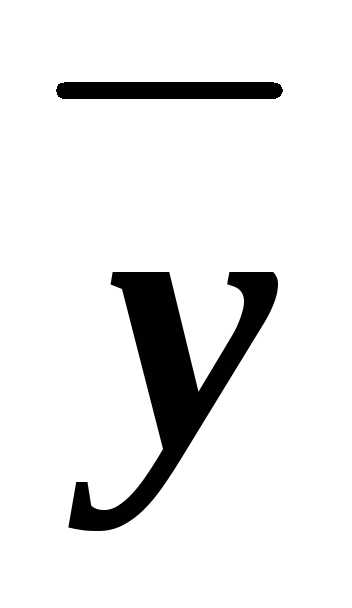
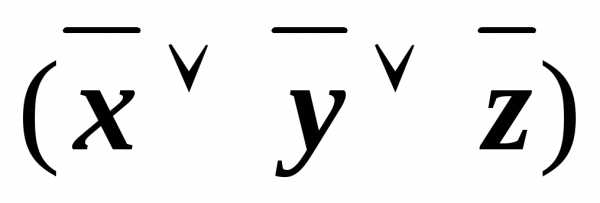 (x&
(x& ))
))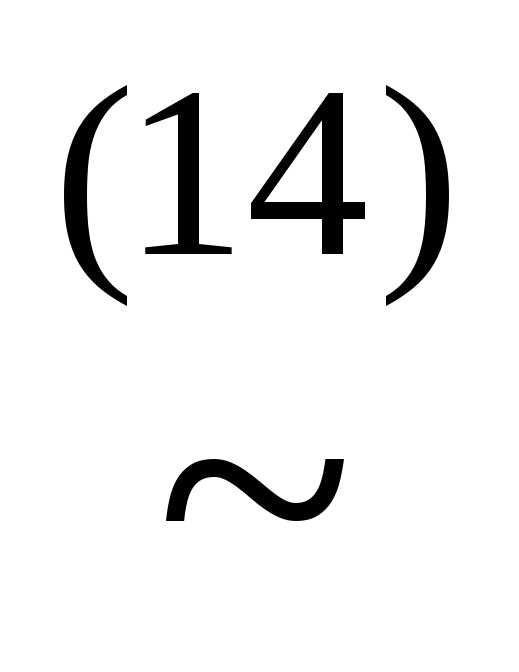 (xz)&
(xz)&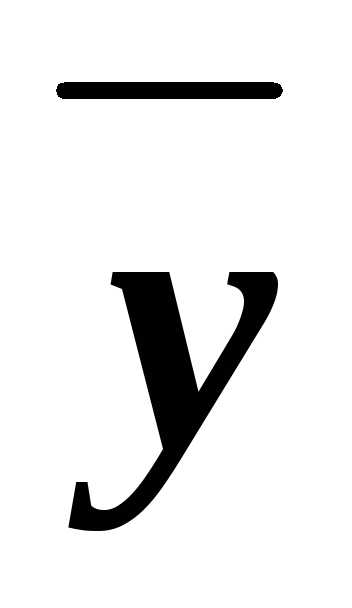 &&
&&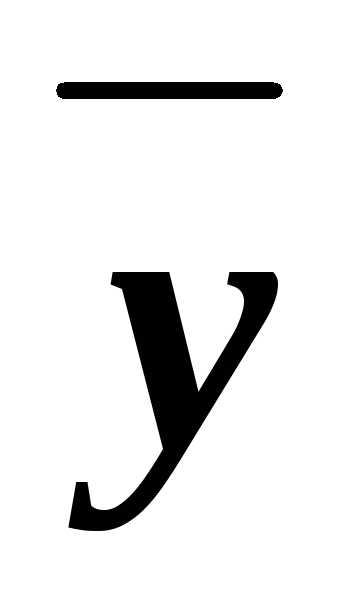
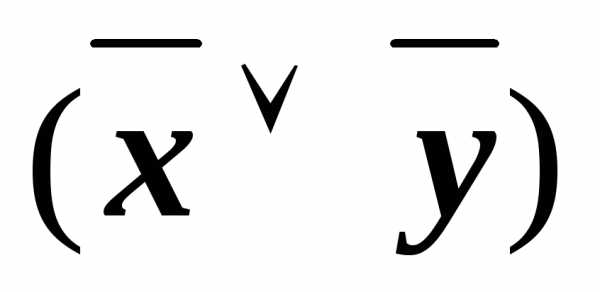 (xz)&
(xz)&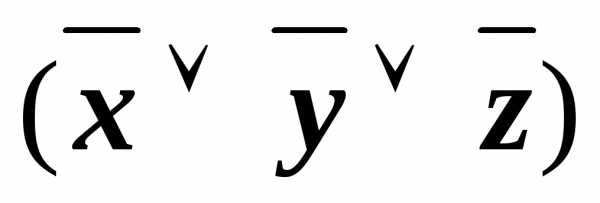 &
&

Получили КНФ формулы. Теперь преобразуем КНФ по алгоритму получения всех условий совершенства:
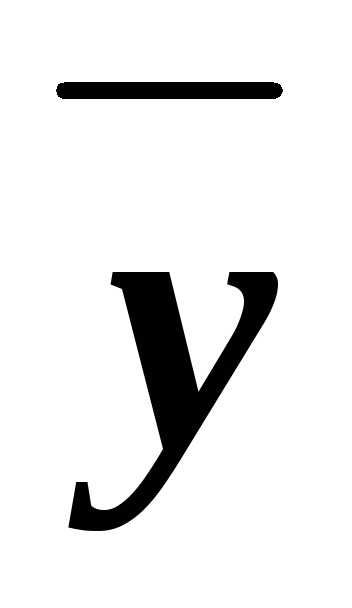 (xyz)&(x
(xyz)&(x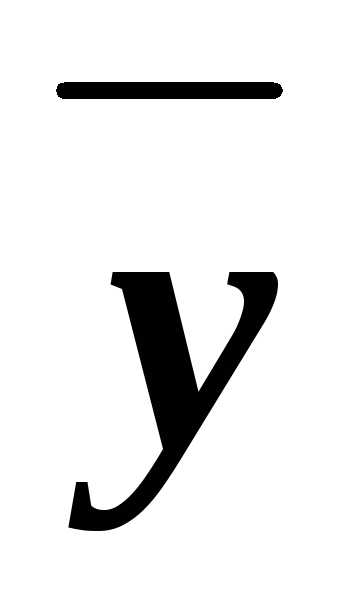 z)&(x
z)&(x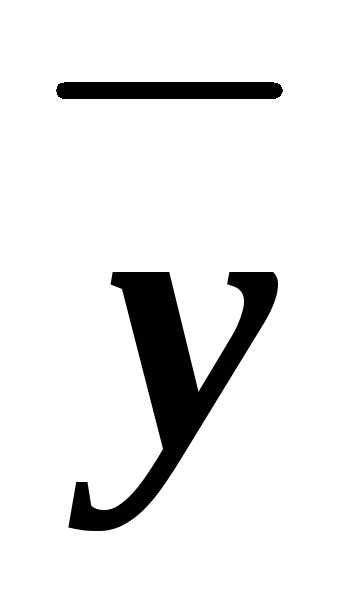 )&
)& &
&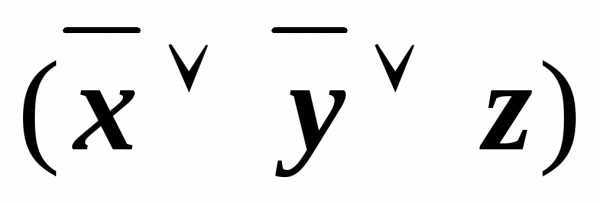
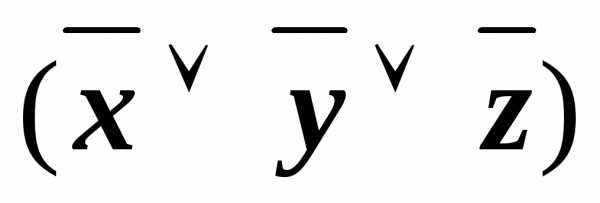
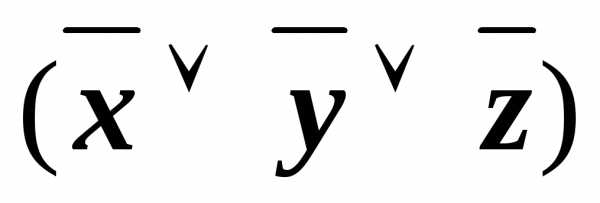 (xyz)&(x
(xyz)&(x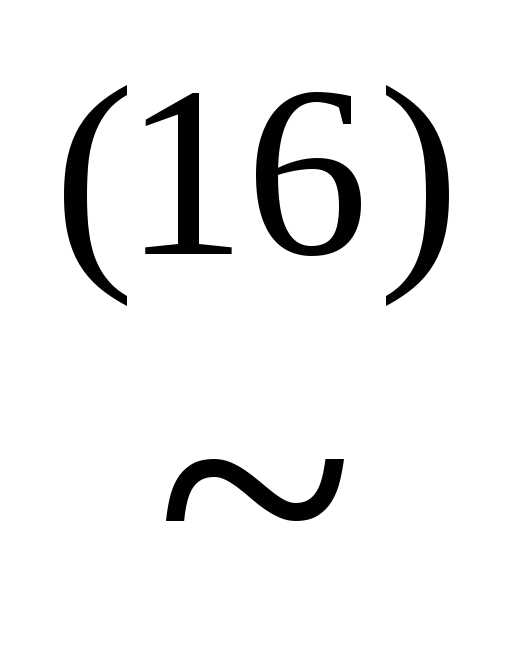 z)&(x
z)&(x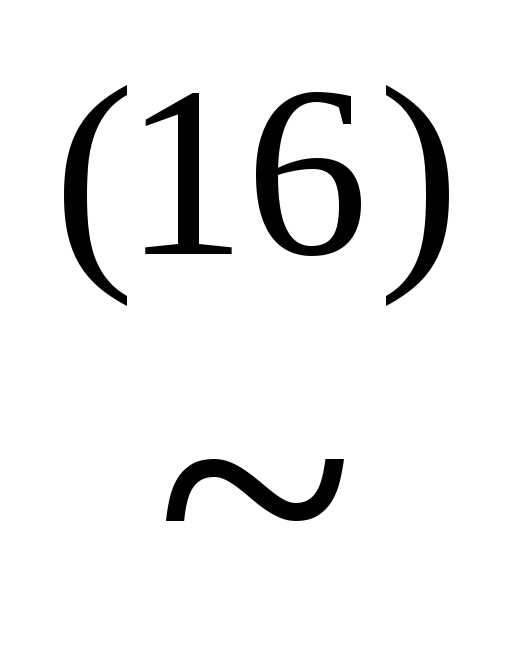 z)&(x
z)&(x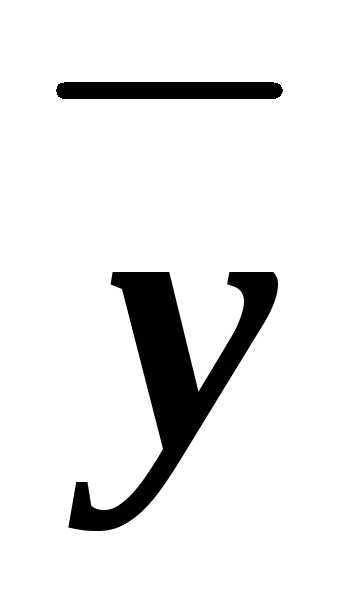
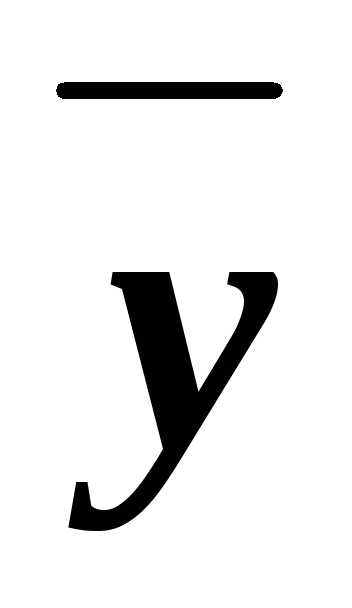 )&
)& &
&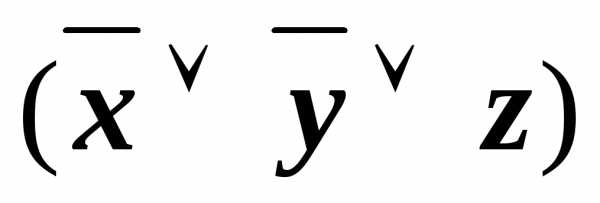 &
&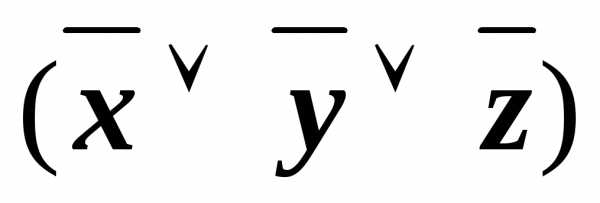

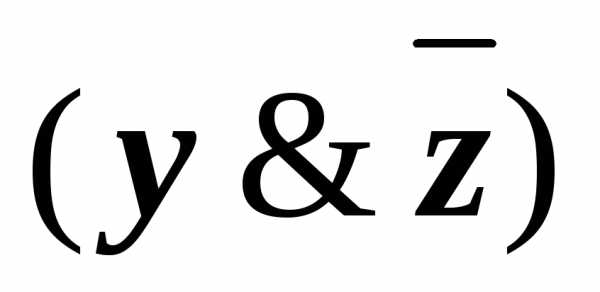 (xyz)&(x
(xyz)&(x z)&(x
z)&(x
 )&
)& &
&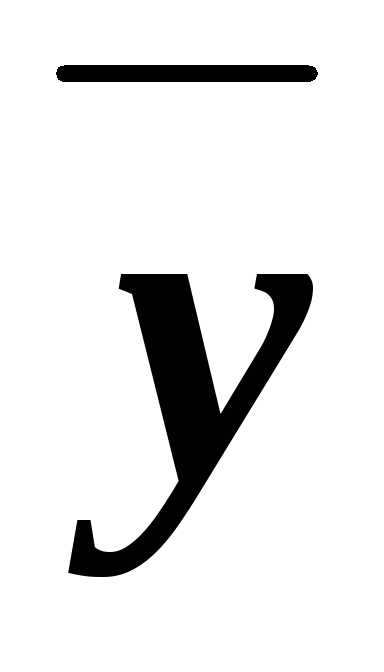
(1) Одновременно заменили | на отрицание операции &,и на отрицание.
(2) Одновременно применили закон двойного отрицания и заменили наи его отрицание.
(3) Операцию заменили на.
(4) Применили закон де Моргана.
(5) Заменили на.
(6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания.
(8) Воспользовались ассоциативностью и коммутативностью .
(9) 1-й и 2-й конъюнкты объединили в один с помощью дистрибутивности & относительно .
(10) К подформуле 
 применили закон дистрибутивности.
применили закон дистрибутивности.
(11) Воспользовались тем, что  у~1.
у~1.
(12) Применили сложную дизъюнкцию относительно .
(13) Применили законы исключённого третьего и идемпотентности.
(14) В 1-й и 2-й дизъюнкты добавили недостающие литеры и разбили их по два дизъюнкта каждую (1-я операция приведения к СКНФ).
(15) Операцию, аналогичную (14) проделали с 3-м и 4-м дизъюнктами.
(16) Опустили лишние дизъюнкты.
СДНФ формулы существует и единственна.
Существование СКНФ для любой формулы вытекает из алгоритма её построения.
Другой способ построения СКНФА основывается на следующей эквиваленции:
A(х1, х2,
…, хn)~ .
.
Другими словами,
формула A(х1, х2,
…, хn)
в своей СДНФ содержит те и только те
конъюнкты вида (4.2), значения которых
равны 0 при xi=1i для всех i=1,
2, …, n.
Например, для формулы А=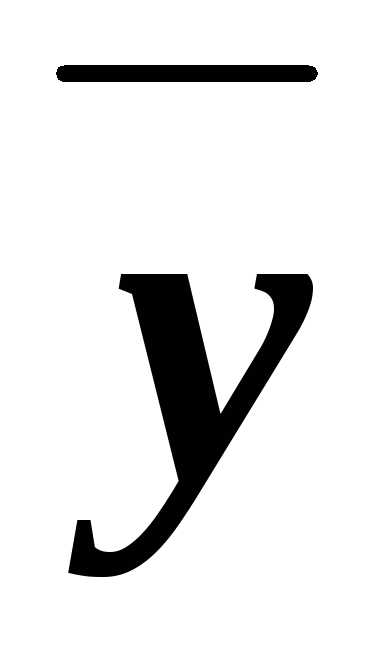 (
(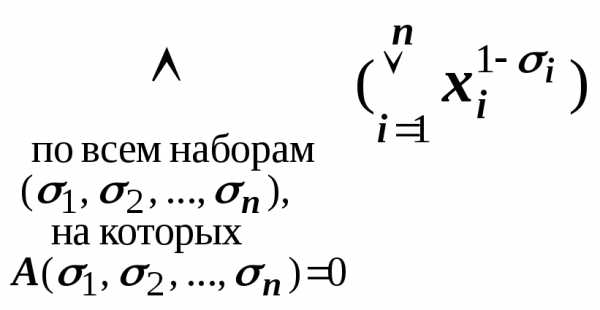 у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х ,
, 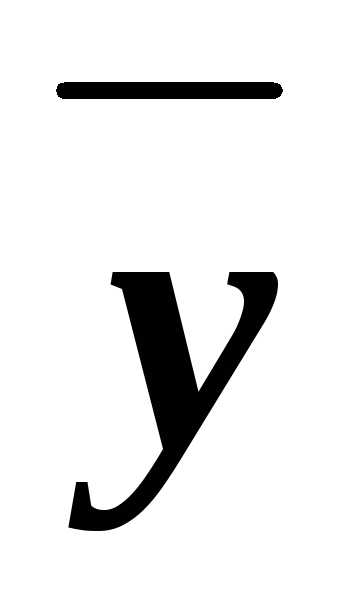 у и
у и 
 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 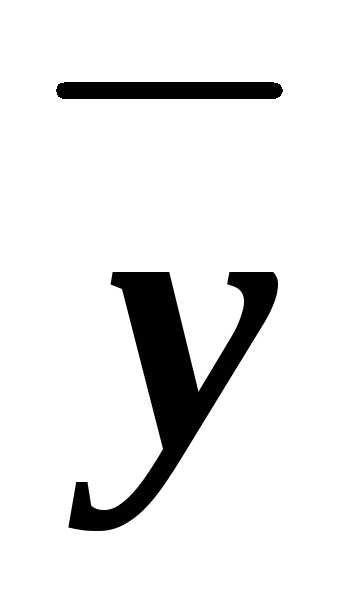
 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
Таким образом,
СКНФA(х1, х2,
…, хn)= .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
Упражнение 4.4.С помощью таблиц истинности привести формулы упражнения 3.4 к СКНФ.
Решение. д). 1. Составим таблицу истинности формулы (она у нас уже составлена, см. решение задачи д) упражнения 4.2):
2. Выберем те наборы значений переменных, при которых формула принимает значение 0: (0, 0, 1), (0, 1, 1).
3. Составим соответствующие им дизъюнкты: xy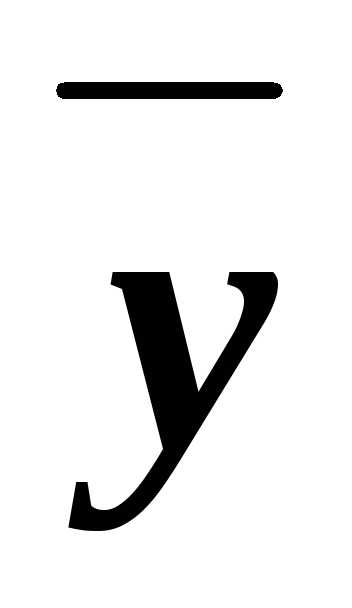 ,x
,x
 .
.
4. Составим из них КНФ: (xy )&(x
)&(x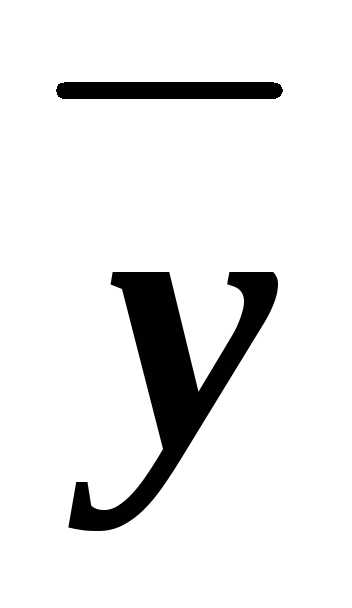
 ).
).
Ответ: д)
СКНФA=(xy )&(x
)&(x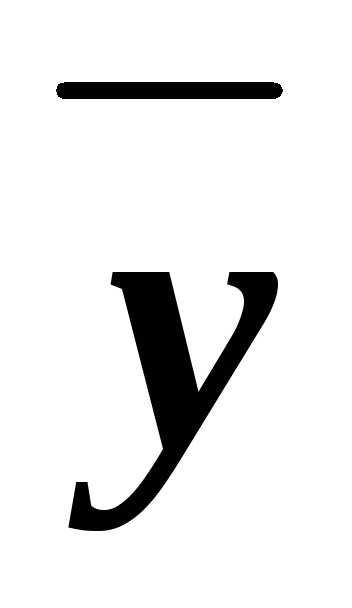
 ).
).
4.3. Принцип двойственности. Операция & называется двойственной к , двойственной к &. Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.
Определение 8. Формула A* называется двойственной к А, если A* получается из A заменой в ней каждой операции на двойственную.
Очевидно, если A* двойственна к A, то A двойственна к A*. Поэтому говорят о взаимно двойственных формулах.
Очевидно также, что если формулы А и В равносильны, то равносильны и двойственные им А* и В*. Кроме того, если A*(х1, х2, …, хп) двойственна к A(х1, х2, …, хп), то ~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.
Определение 9. Формула А называется самодвойственной, если A*~A.
Из определения следует, что формула A самодвойственна, если при замене 0 на 1, и 1 на 0 её таблица истинности не меняется (естественно, меняются между собой только строки). Очевидно, формула самодвойственна тогда и только тогда, когда на всех противоположных значениях переменных формула принимает противоположные значения.
studfiles.net
Дизъюнктивные и конъюнктивные совершенные нормальные формы
Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).
Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.
Примеры: y, ¬ y, х1 ∧ ¬ х2 ∧ х3 ∧ х4
Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.
ДНФ записывается в следующей форме: F1 ∨ F2 ∨ … ∨ Fn, где Fi — элементарная конъюнкция
Примеры: ¬ х1 ∧ х2 ∨ х1 ∧ ¬ х2 ∨ х1 ∧ ¬ х2 ∧ х3, ¬ y1 ∨ y1 ∧ y2 ∨ ¬ y2
Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой конъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Пример: (¬ х1 ∧ х2 ∧ х3) ∨ (х1 ∧ ¬ х2 ∧ х3) ∨ (х1 ∧ х2 ∧ ¬ х3)
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.
Примеры: ¬ х3, х1 ∨ х2, х1 ∨ х2 ∨ ¬ х3
Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
КНФ записывается в следующей форме: F1 ∧ F2 ∧ … ∧ Fn, где Fi — элементарная дизъюнкция
Примеры: (х1 ∨ ¬ х2) ∧ х3, (х1 ∨ х2) ∧ ( ¬ х1 ∨ х2 ∨ х3) ∧ ( х1 ∨ ¬ х2 ∨ ¬ х3)
Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Пример: (х1 ∨ х2 ∨ х3) ∧ ( ¬ х1 ∨ ¬ х2 ∨ х3)
Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ.
Алгоритм построения СДНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно единице.
- Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Алгоритм построения СКНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно нулю.
- Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные дизъюнкции связываем операциями конъюнкции.
Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае — СКНФ.
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
| x | y | z | F (x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Проверим полученную формулу. Для этого построим таблицу истинности функции.
| x | y | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F (x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.
informatics-lesson.ru
4.2. Конъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.
Определение 5. Дизъюнкция
(4.2)
называется элементарной дизъюнкцией или дизъюнктом.
Как и в случае конъюнктов, существует 2n различных элементарных дизюъюнкций от n переменных. При этом значение элементарной дизюъюнкции вида (4.2) равно 0 тогда и только тогда, когда xi=1i для всех i=1, 2, …, n.
Конъюнкция вида (4.1) называется также конституентой нуля.
Определение 6. Конъюнктивной нормальной формой формулы А (КНФА) называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Пример 4.2. Для
формулы А= (
( у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.
Как и в случае ДНФ, КНФ формулы неединствен. Их можно составить сколько угодно. К КНФ формулы можно прийти по следующему алгоритму:
I шаг: Приведение операций |, , , , к операциям &, или их отрицаниям:
1. Если в формуле участвуют операции |, , и , то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций.
2. Если в формуле участвует операция , то от неё с помощью закона т) упражнения 3.2 переходим к операции .
3. Если в формуле участвует операция , то от неё с помощью закона п) упражнения 3.2 преходим к операции .
II шаг. Отнесение отрицаний к пропозициональным переменным.
4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным.
5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются.
III шаг. Получение КНФ.
С помощью свойства дистрибутивности относительно & все подформулы вида A(B1&B2&…&Bk) приводим к подформулам вида (AB1)&(AB2)&…&(ABk) до тех пор, пока не получим конъюнкцию элементарных дизъюнкций.
Таким образом, мы доказали, что любая формула эквивалентна некоторой КНФ.
Очевидно, А&А&…&А~А, и поэтому в КНФ элементарная дизъюнкция может повторяться сколько угодно раз. В результате мы приходим к тому, КНФ формулы можно построить сколько угодно.
Потребуем, чтобы КНФ удовлетворяла следующим четырём свойствам совершенства:
1. Каждый дизъюнкт КНФ формулы содержит все переменные или их отрицания, входящие в формулу.
2. Все дизъюнкты, входящие в КНФ, различны.
3. Ни один дизъюнкт, из которых состоит КНФ, не содержит одновременно переменную и её отрицание.
4. Ни один дизъюнкт не содержит одну же литеру два и более раз.
Определение 7. КНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной конъюнктивной нормальной формой данной формулы (СКНФ).
Для того, чтобы получить СКНФ формулы А, достаточно сначала формулу привести к КНФА, а затем применить к полученной КНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную КНФА, удовлетворяющие всем условиям совершенства:
1. Если в КНФА какой-либо дизъюнкт В не содержит переменную хi или её отрицание, то используя
равносильности B~В(хi&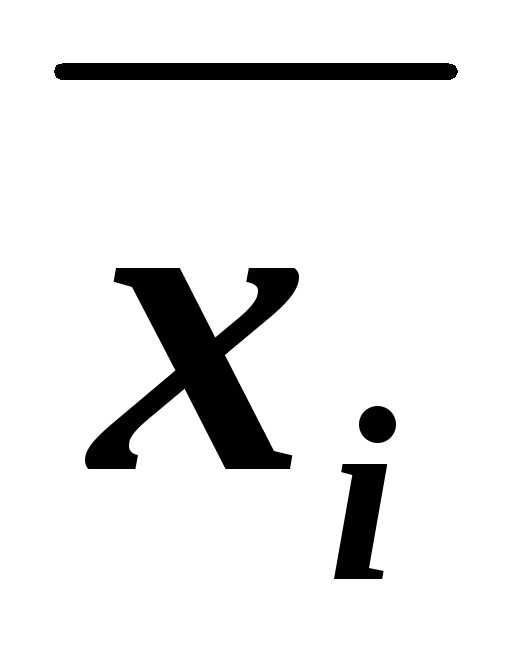 )~
~(Вхi)&(B
)~
~(Вхi)&(B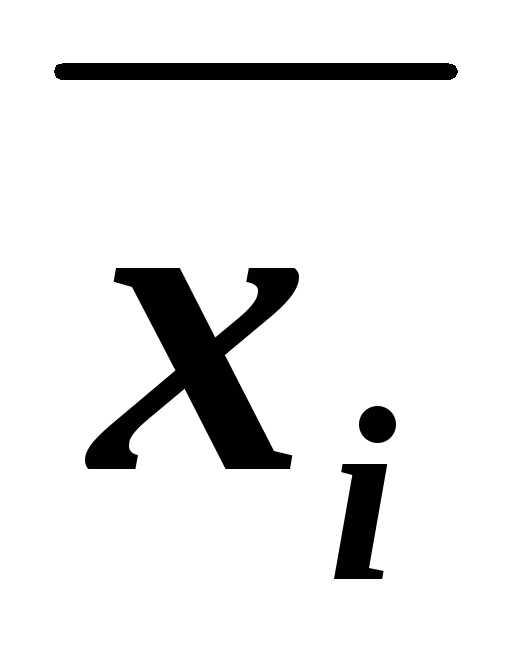 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B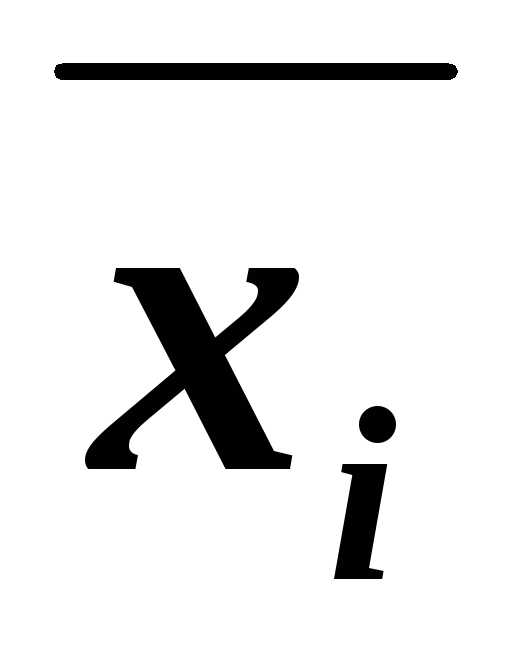 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание 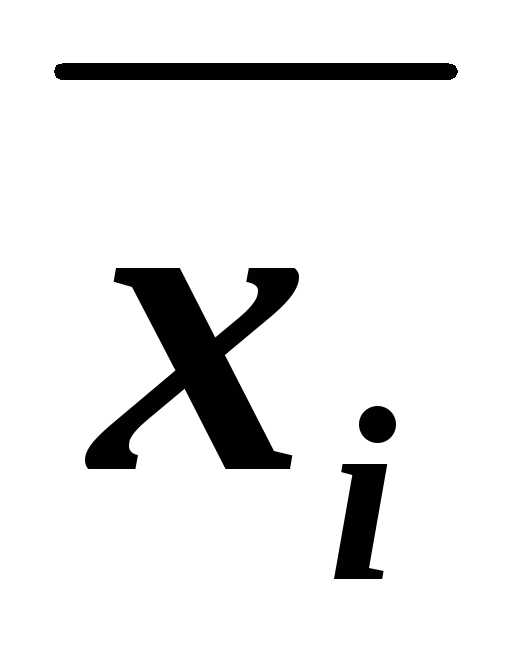 .
.
2. Если в КНФА входят два или более одинаковых дизъюнкта B, то лишние отбрасываем, пользуясь равносильностью B&B&…&B~B.
3. Если некоторый
дизъюнкт В,
входящий в КНФА,
содержит переменную хi и её отрицание 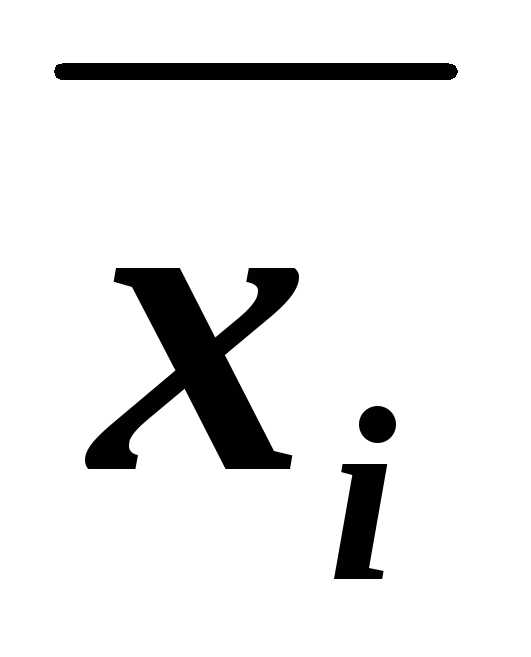 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
4. Если некоторый
дизъюнкт, входящий в КНФА,
содержит одну и ту же литеру 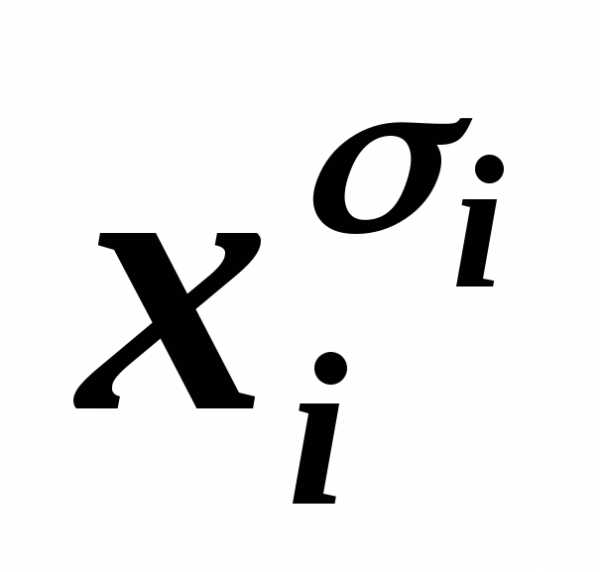 дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью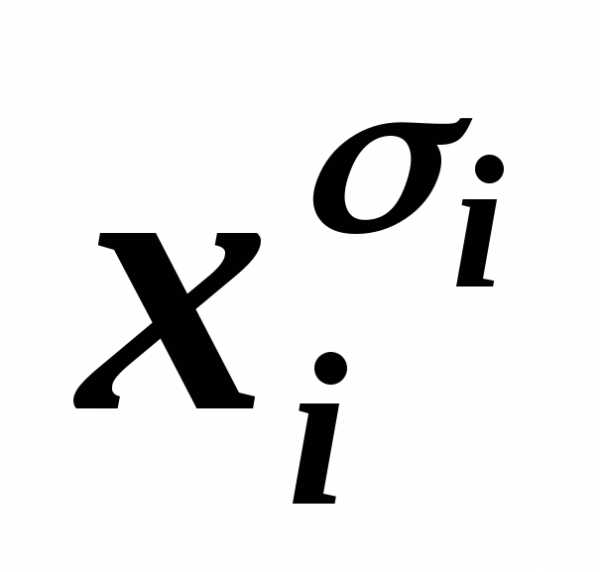
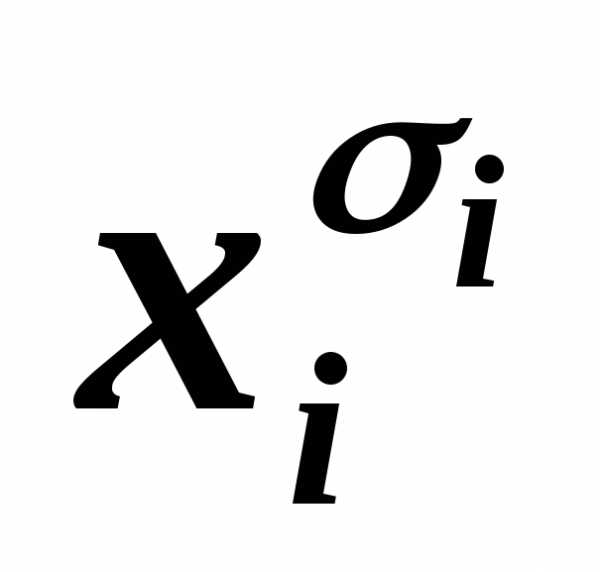 …
…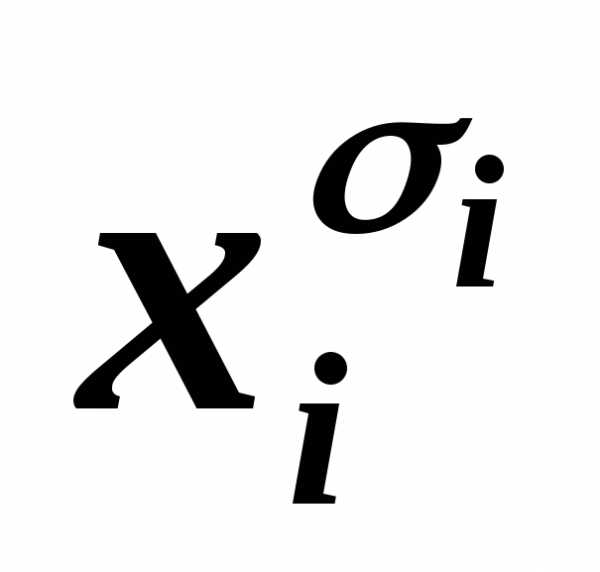 ~
~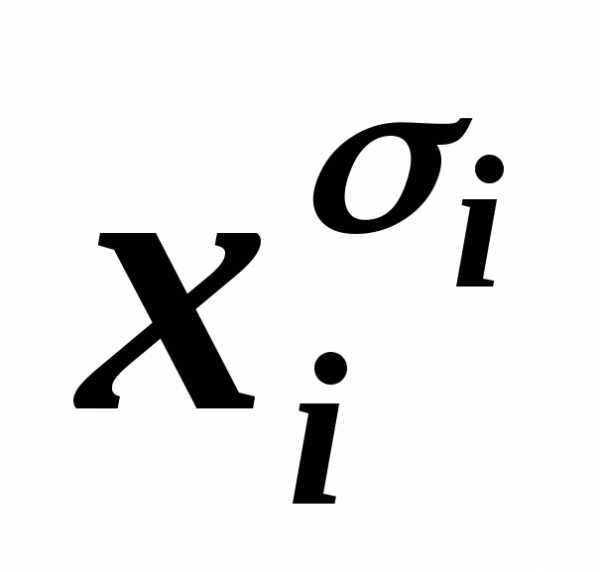 ,
лишние отбрасываем.
,
лишние отбрасываем.
Упражнение 4.3.С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СКНФ.
Решение. з) Приведём формулу к КНФ:
(x| )(z
)(z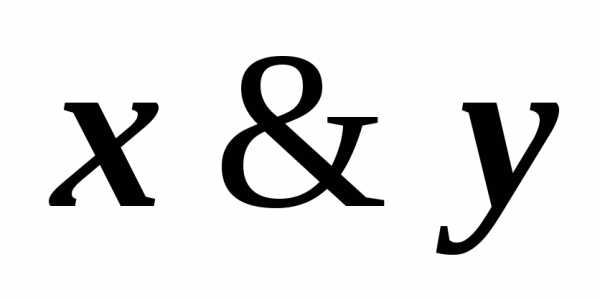 )
)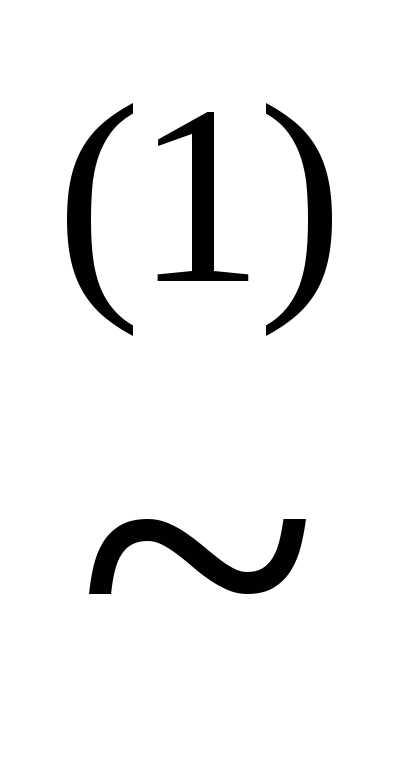 (
(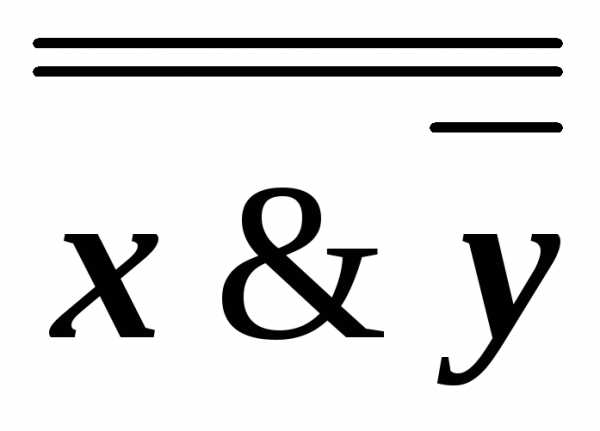 )(z
)(z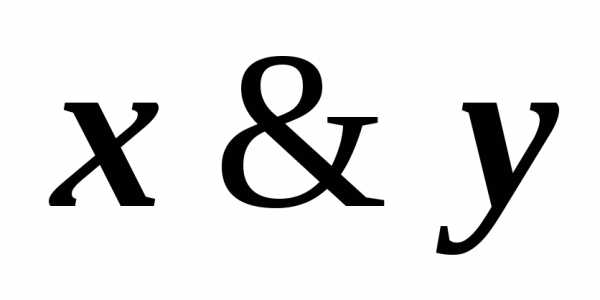 )
)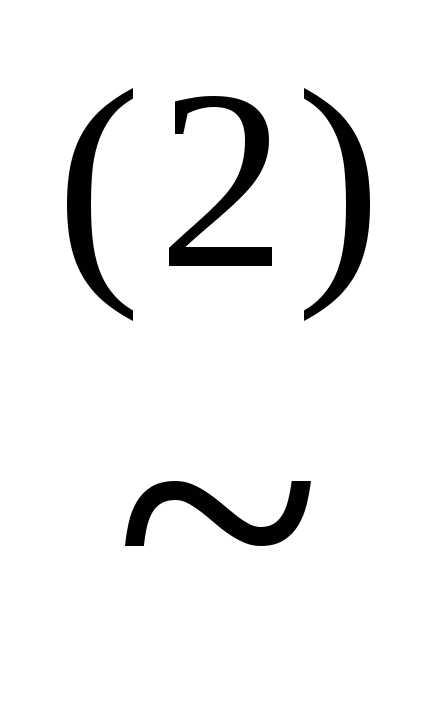 (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)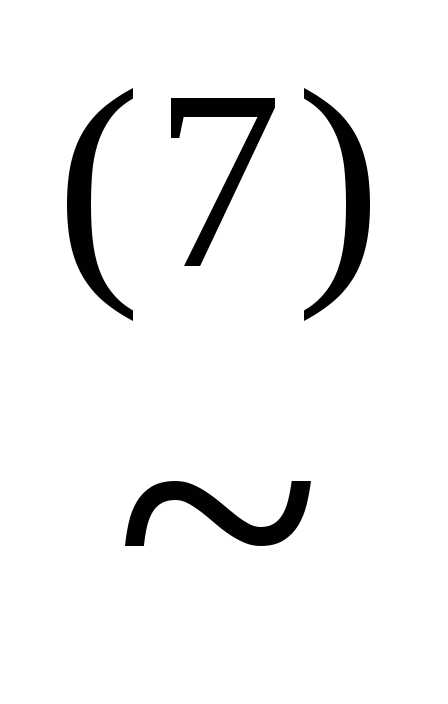
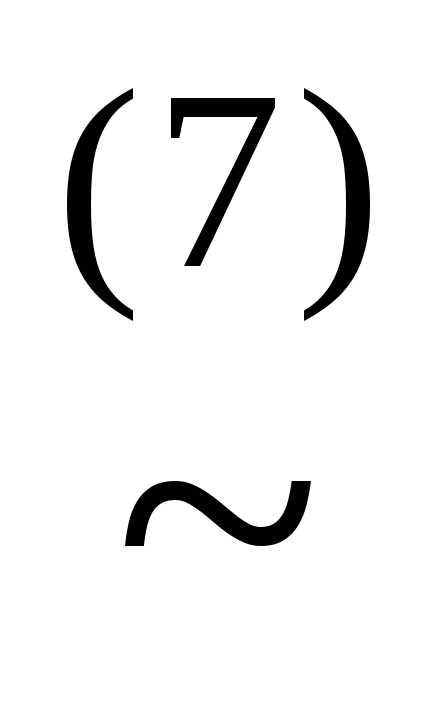 (x&
(x& )(
)( (x&
(x& ))
))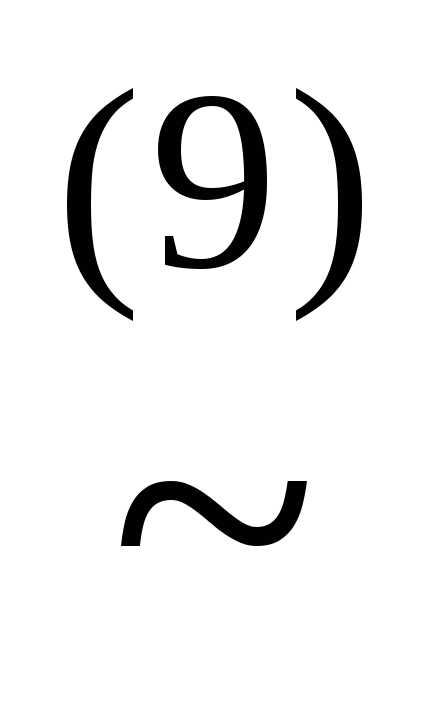
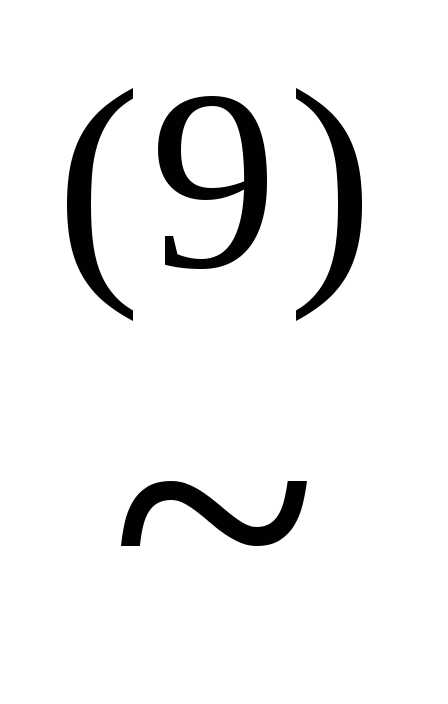 (x&(
(x&(
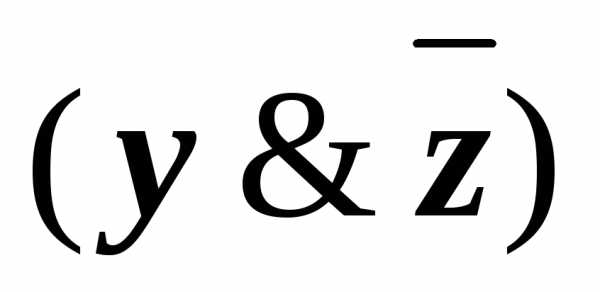 )))
)))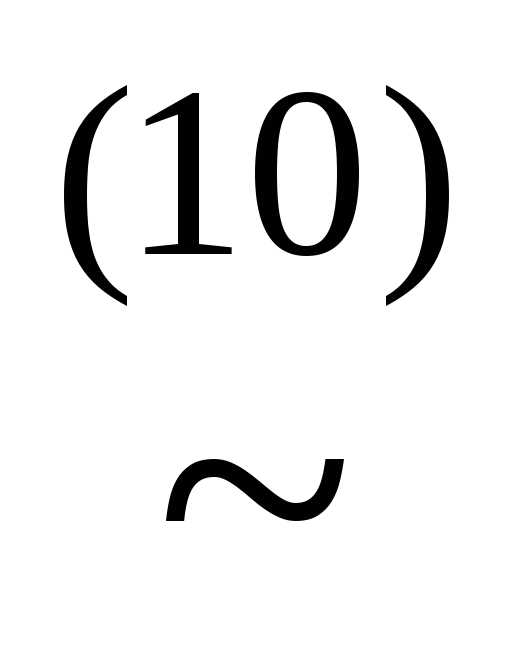 (x&((
(x&(( у)&
у)&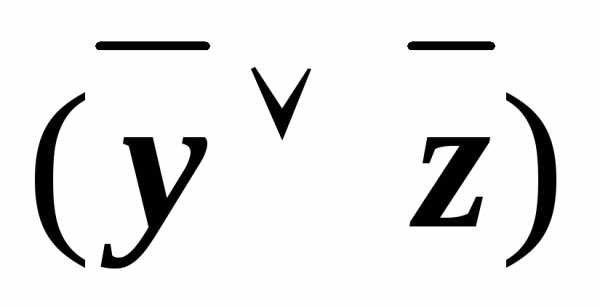 )))
)))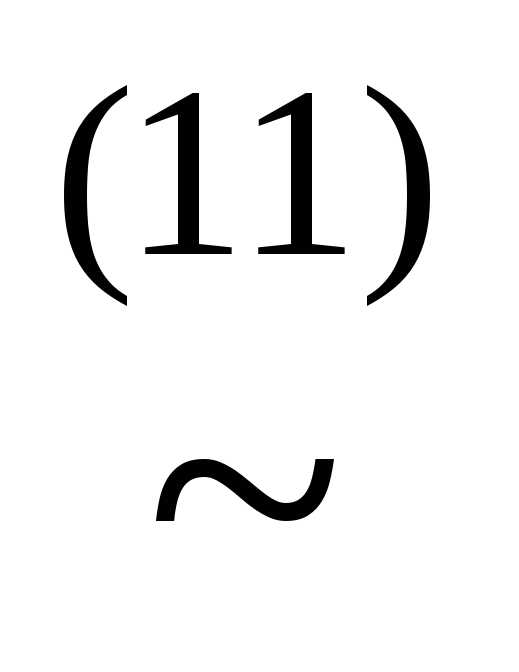
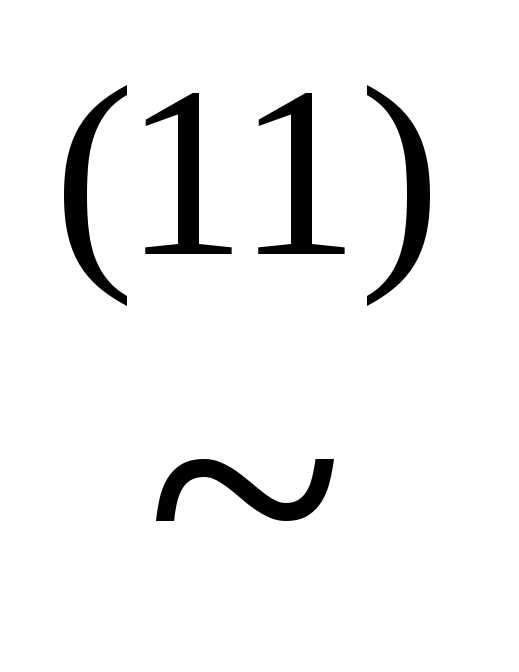 (x&
(x&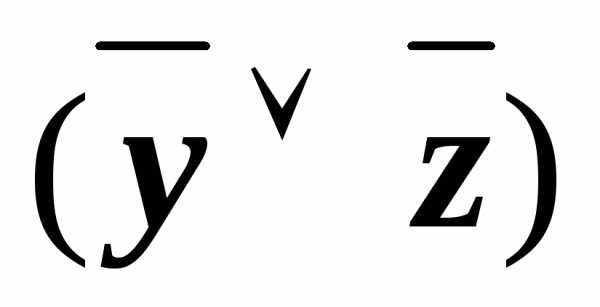 ))
))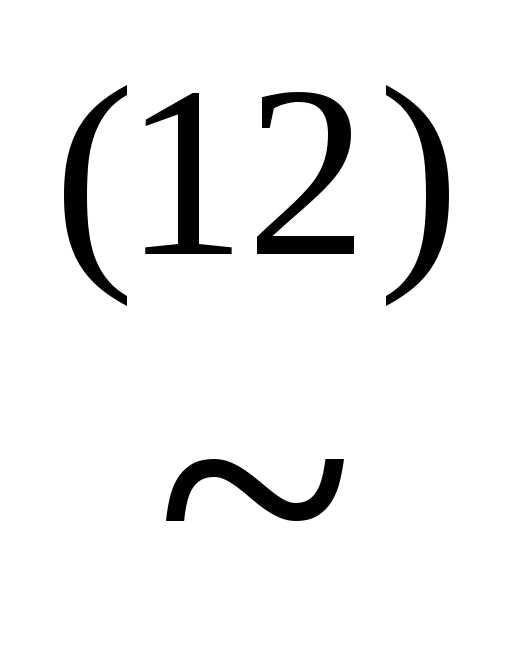 (xz)&
(xz)&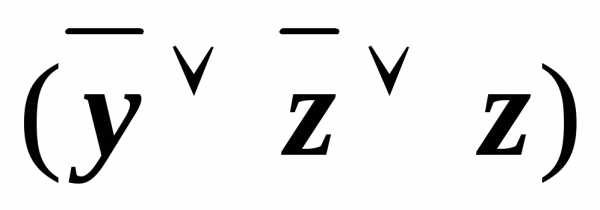 &&
&&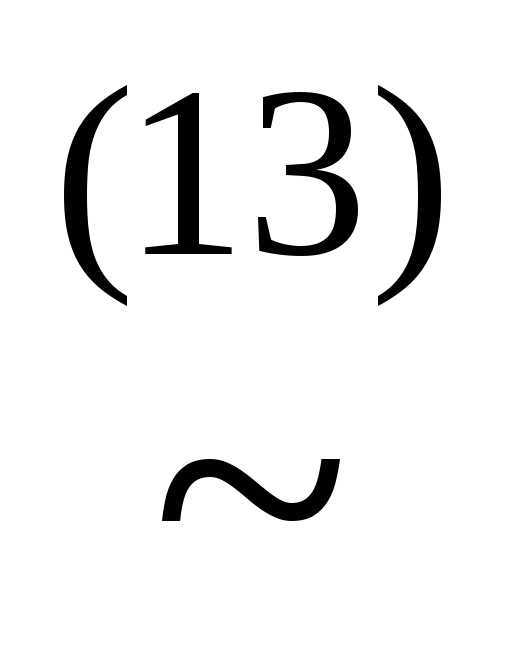
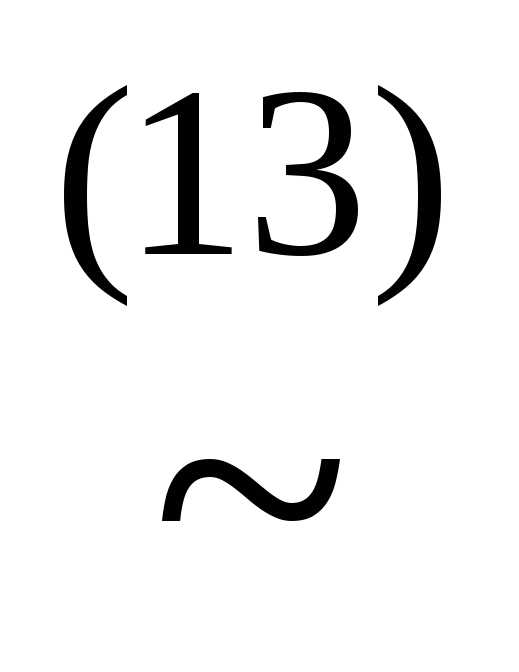 (xz)&
(xz)&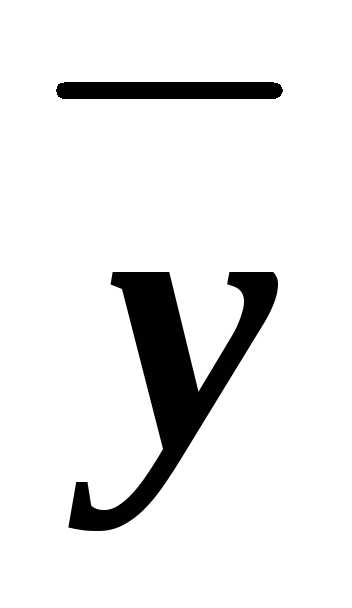 &
&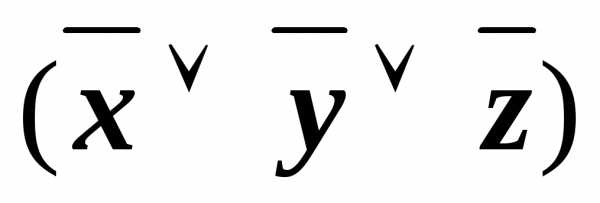
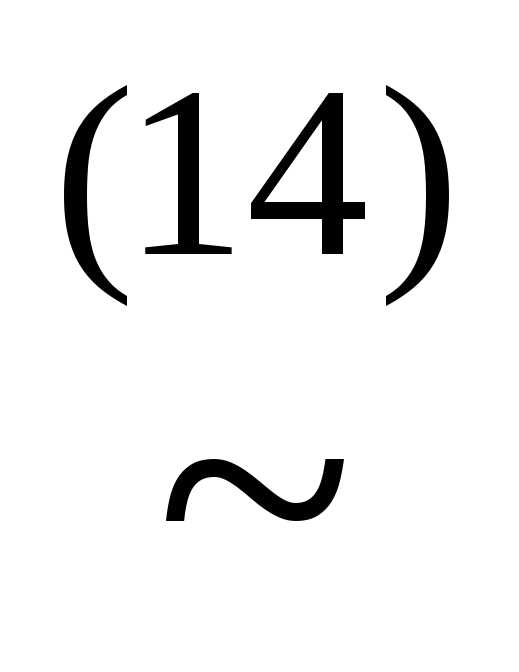
Получили КНФ формулы. Теперь преобразуем КНФ по алгоритму получения всех условий совершенства:
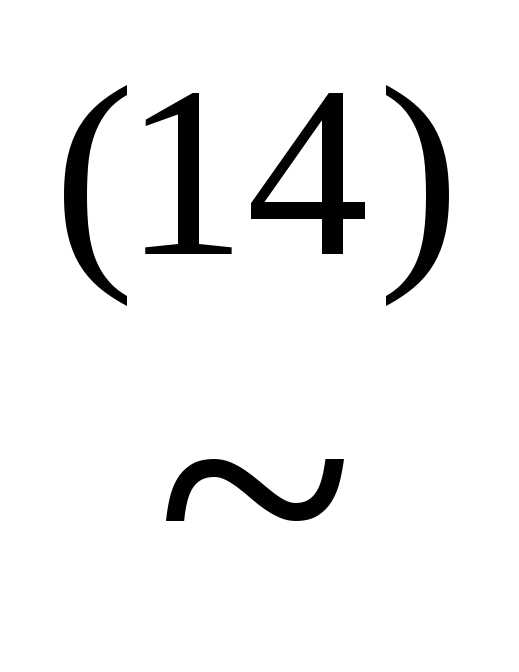 (xyz)&(x
(xyz)&(x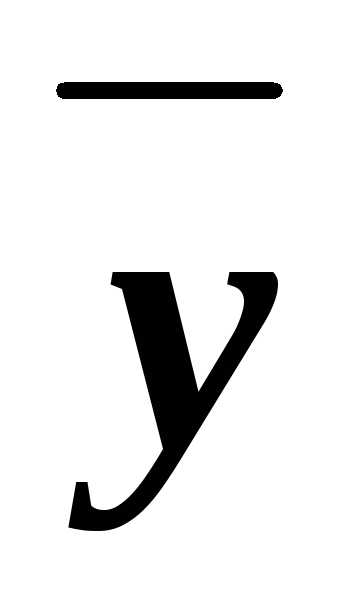 z)&(x
z)&(x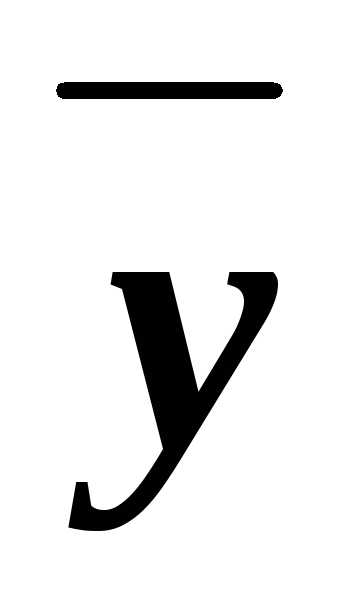 )&
)&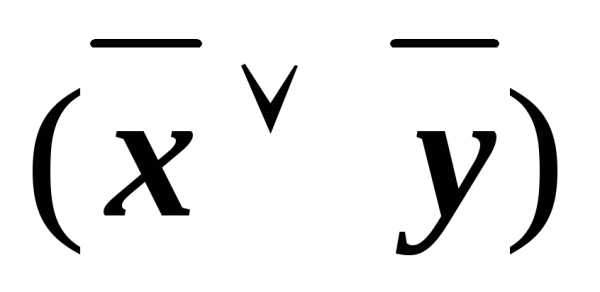 &
&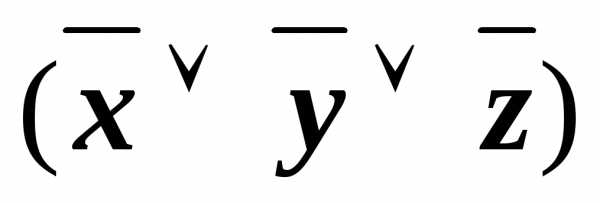

 (xyz)&(x
(xyz)&(x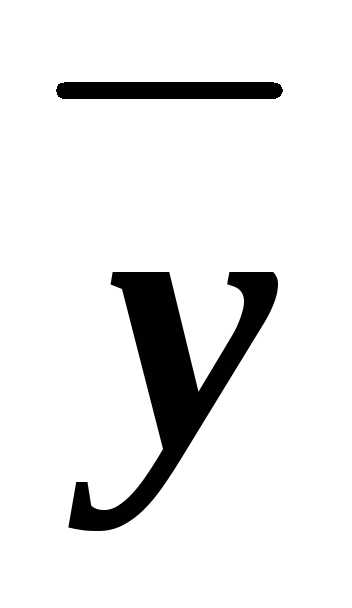 z)&(x
z)&(x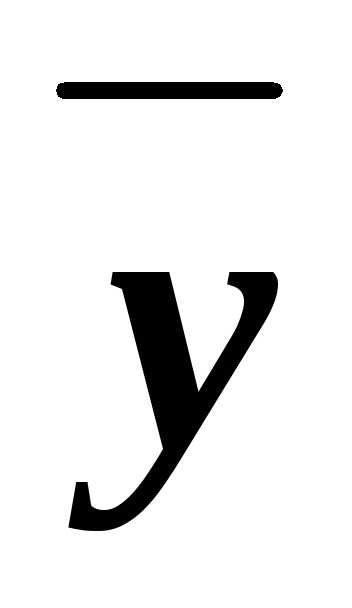 z)&(x
z)&(x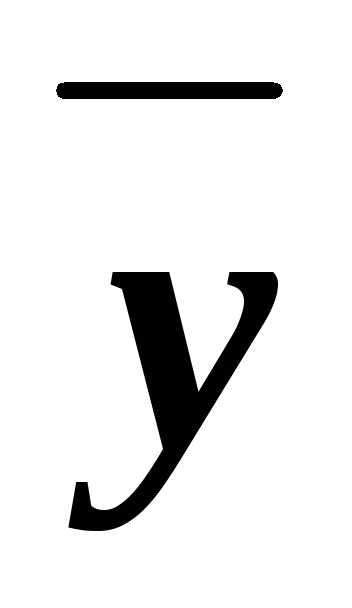
 )&
)&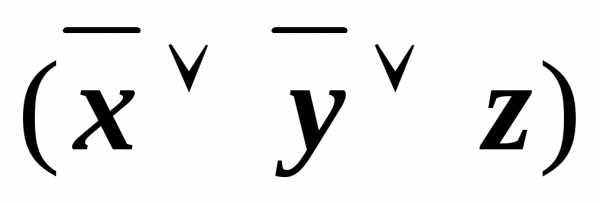 &
&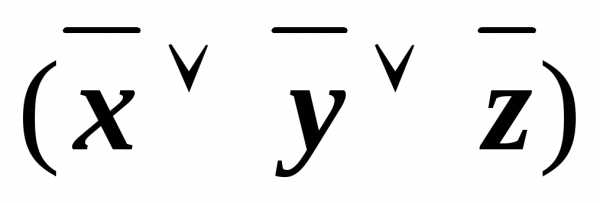 &
&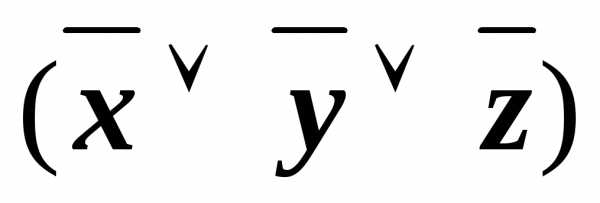
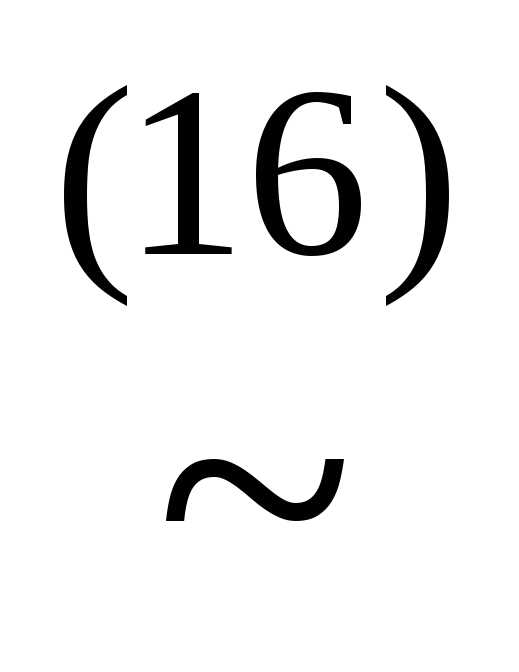
 (xyz)&(x
(xyz)&(x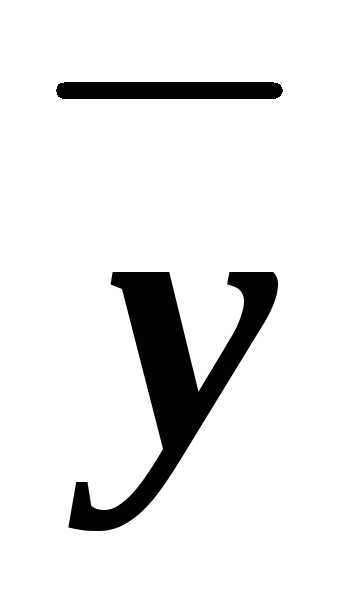 z)&(x
z)&(x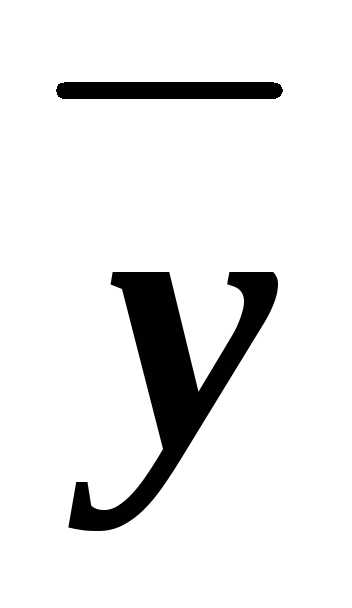
 )&
)&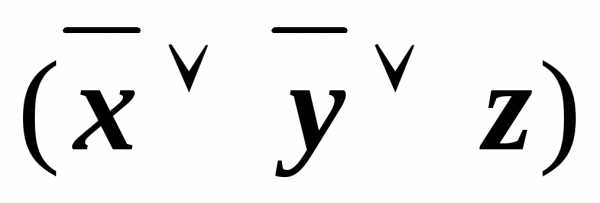 &
&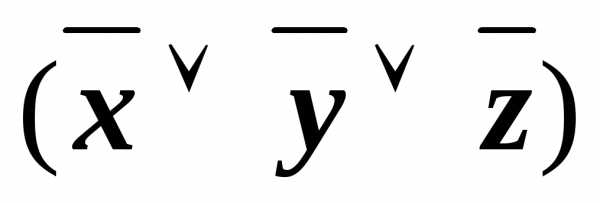
(1) Одновременно заменили | на отрицание операции &,и на отрицание.
(2) Одновременно применили закон двойного отрицания и заменили наи его отрицание.
(3) Операцию заменили на.
(4) Применили закон де Моргана.
(5) Заменили на.
(6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания.
(8) Воспользовались ассоциативностью и коммутативностью .
(9) 1-й и 2-й конъюнкты объединили в один с помощью дистрибутивности & относительно .
(10) К подформуле 
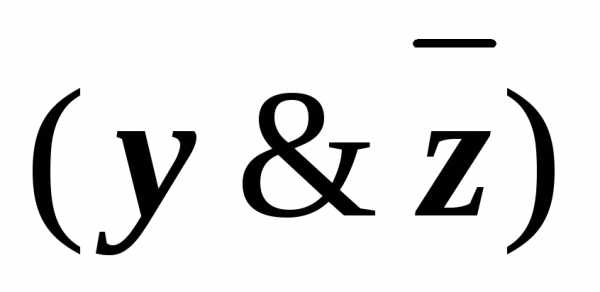 применили закон дистрибутивности.
применили закон дистрибутивности.
(11) Воспользовались тем, что  у~1.
у~1.
(12) Применили сложную дизъюнкцию относительно .
(13) Применили законы исключённого третьего и идемпотентности.
(14) В 1-й и 2-й дизъюнкты добавили недостающие литеры и разбили их по два дизъюнкта каждую (1-я операция приведения к СКНФ).
(15) Операцию, аналогичную (14) проделали с 3-м и 4-м дизъюнктами.
(16) Опустили лишние дизъюнкты.
СДНФ формулы существует и единственна.
Существование СКНФ для любой формулы вытекает из алгоритма её построения.
Другой способ построения СКНФА основывается на следующей эквиваленции:
A(х1, х2,
…, хn)~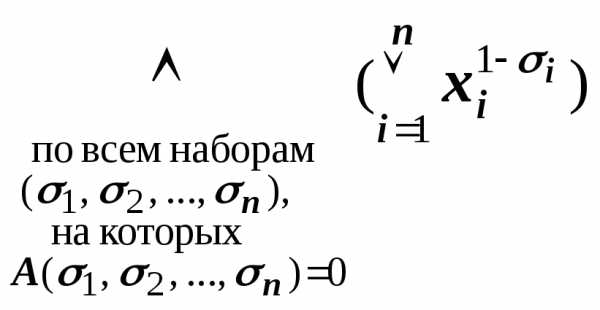 .
.
Другими словами,
формула A(х1, х2,
…, хn)
в своей СДНФ содержит те и только те
конъюнкты вида (4.2), значения которых
равны 0 при xi=1i для всех i=1,
2, …, n.
Например, для формулы А= (
( у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х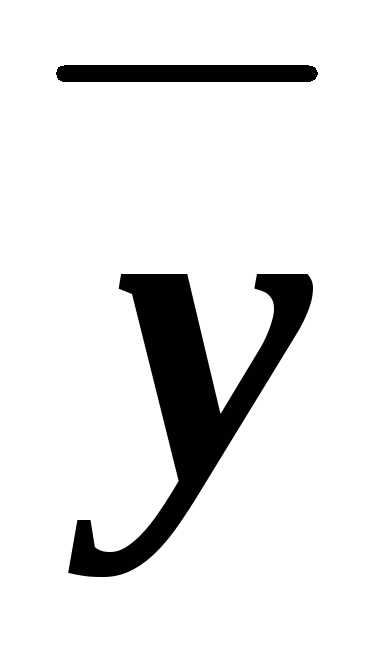 ,
,  у и
у и 
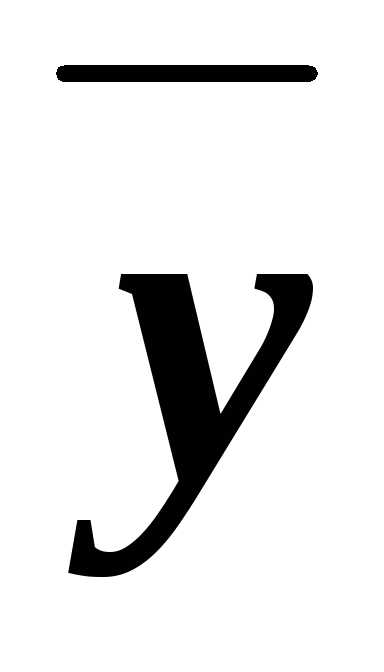 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 
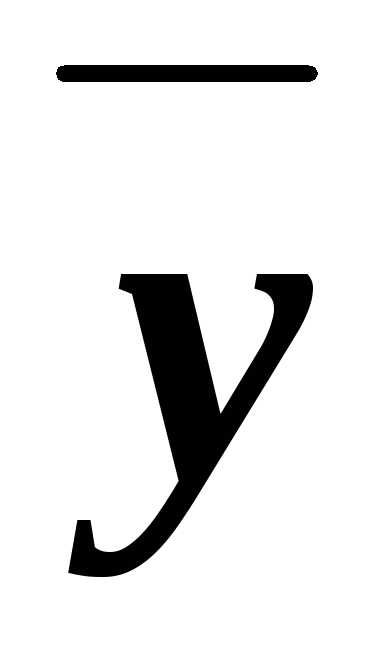 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
Таким образом,
СКНФA(х1, х2,
…, хn)=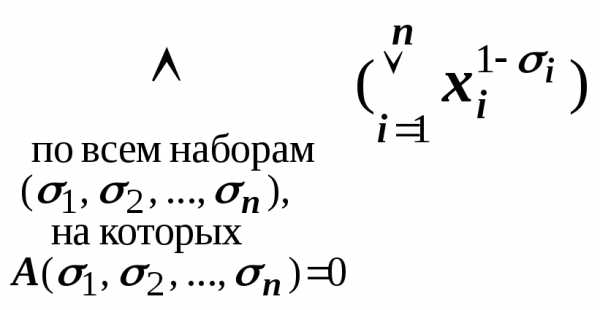 .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
Упражнение 4.3.С помощью таблиц истинности привести формулы упражнения 3.4 к СКНФ.
Решение. д). 1. Составим таблицу истинности формулы (она у нас уже составлена, см. решение задачи д) упражнения 4.2):
2. Выберем те наборы значений переменных, при которых формула принимает значение 0: (0, 0, 1), (0, 1, 1).
3. Составим соответствующие им дизъюнкты: xy ,x
,x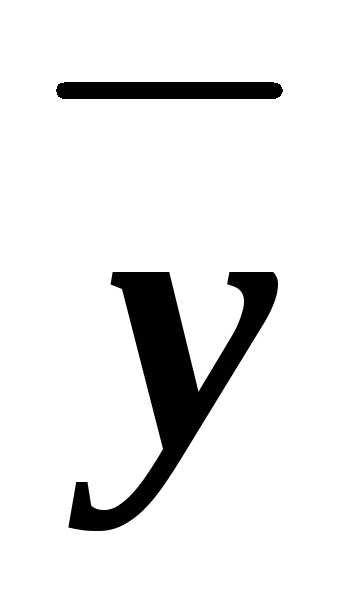
 .
.
4. Составим из них КНФ: (xy )&(x
)&(x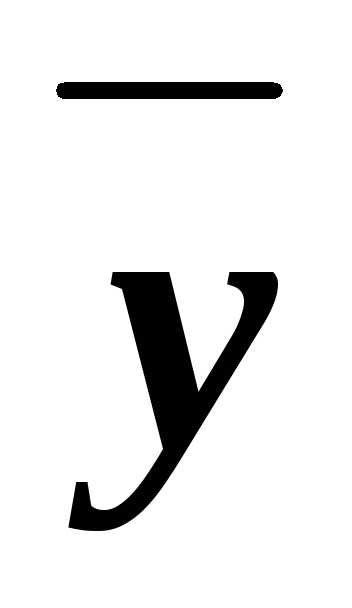
 ).
).
Ответ: д)
СКНФA=(xy )&(x
)&(x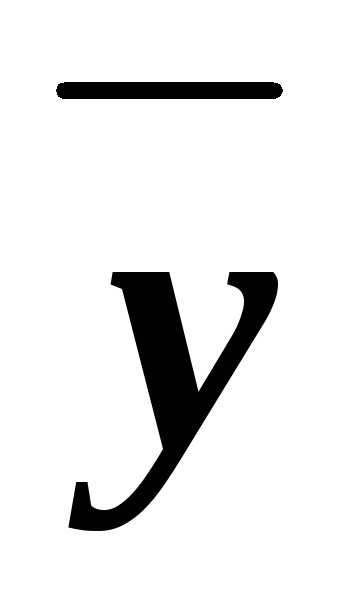
 ).
).
4.3. Принцип двойственности. Операция & называется двойственной к , двойственной к &. Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.
Определение 8. Формула A* называется двойственной к А, если A* получается из A заменой в ней каждой операции на двойственную.
Очевидно, если A* двойственна к A, то A двойственна к A*. Поэтому говорят о взаимно двойственных формулах.
Очевидно также, что если формулы А и В равносильны, то равносильны и двойственные им А* и В*. Кроме того, если A*(х1, х2, …, хп) двойственна к A(х1, х2, …, хп), то ~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.
Определение 9. Формула А называется самодвойственной, если A*~A.
Из определения следует, что формула A самодвойственна, если при замене 0 на 1, и 1 на 0 её таблица истинности не меняется (естественно, меняются между собой только строки). Очевидно, формула самодвойственна тогда и только тогда, когда на всех противоположных значениях переменных формула принимает противоположные значения.
studfiles.net
И совершенная конъюнктивная нормальная форма
(КНФ и СКНФ)
Определение 1.Элементарной дизъюнкцией п переменных называется дизъюнкция переменных или их отрицаний.
Элементарная дизъюнкция п переменных может быть записана в виде:
,
Определение 2.Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Для любой формулы алгебры логики путем равносильных преобразований можно получить ее КНФ, причем не единственную.
Например, для формулы имеем:
,то есть КНФ А .
Но так как x , , , , то KHФ
А так как , то КНФ .
Определение 3. КНФ А называется совершенной конъюнктивной нормальной формой формулы А(СКНФ А), если для нее выполнены условия:
1. Все элементарные дизъюнкции, входящие в КНФ А, различны.
2. Все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные.
3. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит двух одинаковых переменных.
4. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание.
Можно доказать, что каждая не тождественно истинная формула имеет единственную СКНФ.
Один из способов получения СКНФ состоит в использовании таблицы истинности для формулы А.
Действительно, получив с помощью таблицы истинности СДНФ А , мы получим СКНФ А , взяв отрицание , то есть СКНФ .
Другой способ получения СКНФ, использующий равносильные преобразования, состоит в следующем:
1. Путем равносильных преобразований формулы А получают одну из КНФ А.
2. Если в полученной КНФ А входящая в нее элементарная дизъюнкция В не содержит переменную xi, то, используя равносильность , элементарную дизъюнкцию В заменяют на две элементарные дизъюнкции и каждая из которых содержит переменную xi.
3. Если в КНФ А входят две одинаковых элементарных дизъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью В&В В .
4. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную хi дважды, то лишнюю можно отбросить, пользуясь равносильностью .
5. Если некоторая элементарная дизъюнкция, входящая в КНФ А , содержит переменную хiи ее отрицание, то и, следовательно, вся элементарная дизъюнкция имеет значение 1, а поэтому ее можно отбросить, как единичный член конъюнкции.
Ясно, что после описанной процедуры будет получена СКНФ А.
Например, для формулы КНФ .
Так как обе элементарные дизъюнкции различны и содержат все переменные (х и у), то первое и второе условия СКНФ А выполнены.
Элементарная дизъюнкция содержит переменную х дважды, но , и поэтому КНФ ; причем ни одна из элементарных дизъюнкций не содержит переменную и ее отрицание. Значит, теперь выполнены все условия СКНФ А, и, следовательно, СКНФ .
§ 12. Проблема разрешимости
Все формулы алгебры логики делятся на три класса:
1) тождественно истинные,
2) тождественно ложные и
3) выполнимые.
Определения тождественно истинной и тождественно ложной формул даны выше.
Формулу А называют выполнимой, если она принимает значение «истина» хотя бы на одном наборе значений входящих в нее переменных и не является тождественно истинной.
В связи с этим возникает задача: к какому классу относится данная формула?
Эта задача носит название проблемы разрешимости.
Очевидно, проблема разрешимости алгебры логики разрешима.
Действительно, для каждой формулы алгебры логики может быть записана таблица истинности, которая и даст ответ на поставленный вопрос.
Однако практическое использование таблицы истинности для формулы А(х1,х2,…,хп) при больших п затруднительно.
Существует другой способ, позволяющий, не используя таблицы истинности, определить, к какому классу относится формула А. Этот способ основан на приведении формулы к нормальной форме (КНФ или ДНФ) и использовании алгоритма, который позволяет определить, является ли данная формула тождественно истинной или не является. Одновременно с этим решается вопрос о том, будет ли формула А выполнимой.
Предположим, что мы имеем критерий тождественной истинности для формул алгебры логики. Рассмотрим механизм его применения.
Применим критерий тождественной истинности к формуле А. Если окажется, что формула А — тождественно истинная, то задача решена. Если же окажется, что формула А не тождественно истинная, то применим критерий тождественной истинности к формуле . Если окажется, что формула А — тождественно истинная, то ясно, что формула — тождественно ложная, и задача решена.
Если же формула не тождественно истинная, то остается единственно возможный результат: формула А выполнима.
Установим теперь критерий тождественной истинности произвольной формулы алгебры логики. С этой целью предварительно сформулируем и докажем критерий тождественной истинности элементарной дизъюнкции.
Теорема 1. Для того, чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание.
Доказательство. Необходимость. Пусть элементарная дизъюнкция тождественно истинна, но в нее одновременно не входит некоторая переменная и ее отрицание. Придадим каждой переменной, входящей в элементарную дизъюнкцию без знака отрицания, значение ложь, а каждой переменной, входящей в элементарную дизъюнкцию под знаком отрицания — значение «истина». Тогда, очевидно, вся элементарная дизъюнкция примет значение ложь, что противоречит условию.
Достаточность. Пусть теперь элементарная дизъюнкция содержит переменную и ее отрицание. Так как , то и вся элементарная дизъюнкция будет тождественно истинной.
Критерий тождественной истинности элементарной дизъюнкции позволяет сформулировать и доказать критерии тождественной истинности произвольной формулы алгебры логики.
Теорема 2.Для того, чтобы формула алгебры логики А была тождественно истинна, необходимо и достаточно, чтобы любая элементарная дизъюнкция, входящая в КНФ А, содержала переменную и ее отрицание.
Доказательство. Необходимость. Пусть А — тождественно истинна. Тогда и КНФ А — тождественно истинна. Но КНФ А А1&А2&…&Ап, где А, — элементарные дизъюнкции (i = 1,2,…, n). Так как КНФ А 1, то Аi 1 (i = 1,2,…, n). Но тогда по теореме 1 каждая элементарная дизъюнкция Aiсодержит переменную и ее отрицание.
Достаточность. Пусть любая элементарная дизъюнкция Ai, входящая в КНФ А, содержит переменную и ее отрицание. Тогда по теореме 1 (i = 1,2…..n). При этом и КНФ .
Например, выясним, является ли формула тождественно истинной.
Так как , то ясно, что каждая элементарная дизъюнкция и , входящая в КНФ А, содержит переменную и ее отрицание. Следовательно, A 1.
Аналогично можно установить критерий тождественной ложности формулы алгебры логики, используя ее ДНФ.
Теорема 3.Для того, чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание.
Теорема 4.Для того, чтобы формула алгебры логики А была тождественно ложной, необходимо и достаточно, чтобы любая конъюнкция, входящая в ДНФ А, содержала переменную и ее отрицание.
infopedia.su
4.2. Конъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.
Определение 5. Дизъюнкция
(4.2)
называется элементарной дизъюнкцией или дизъюнктом.
Как и в случае конъюнктов, существует 2n различных элементарных дизюъюнкций от n переменных. При этом значение элементарной дизюъюнкции вида (4.2) равно 0 тогда и только тогда, когда xi=1i для всех i=1, 2, …, n.
Конъюнкция вида (4.1) называется также конституентой нуля.
Определение 6. Конъюнктивной нормальной формой формулы А (КНФА) называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Пример 4.2. Для
формулы А= (
( у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.
Как и в случае ДНФ, КНФ формулы неединствен. Их можно составить сколько угодно. К КНФ формулы можно прийти по следующему алгоритму:
I шаг: Приведение операций |, , , , к операциям &, или их отрицаниям:
1. Если в формуле участвуют операции |, , и , то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций.
2. Если в формуле участвует операция , то от неё с помощью закона т) упражнения 3.2 переходим к операции .
3. Если в формуле участвует операция , то от неё с помощью закона п) упражнения 3.2 преходим к операции .
II шаг. Отнесение отрицаний к пропозициональным переменным.
4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным.
5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются.
III шаг. Получение КНФ.
С помощью свойства дистрибутивности относительно & все подформулы вида A(B1&B2&…&Bk) приводим к подформулам вида (AB1)&(AB2)&…&(ABk) до тех пор, пока не получим конъюнкцию элементарных дизъюнкций.
Таким образом, мы доказали, что любая формула эквивалентна некоторой КНФ.
Очевидно, А&А&…&А~А, и поэтому в КНФ элементарная дизъюнкция может повторяться сколько угодно раз. В результате мы приходим к тому, КНФ формулы можно построить сколько угодно.
Потребуем, чтобы КНФ удовлетворяла следующим четырём свойствам совершенства:
1. Каждый дизъюнкт КНФ формулы содержит все переменные или их отрицания, входящие в формулу.
2. Все дизъюнкты, входящие в КНФ, различны.
3. Ни один дизъюнкт, из которых состоит КНФ, не содержит одновременно переменную и её отрицание.
4. Ни один дизъюнкт не содержит одну же литеру два и более раз.
Определение 7. КНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной конъюнктивной нормальной формой данной формулы (СКНФ).
Для того, чтобы получить СКНФ формулы А, достаточно сначала формулу привести к КНФА, а затем применить к полученной КНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную КНФА, удовлетворяющие всем условиям совершенства:
1. Если в КНФА какой-либо дизъюнкт В не содержит переменную хi или её отрицание, то используя
равносильности B~В(хi&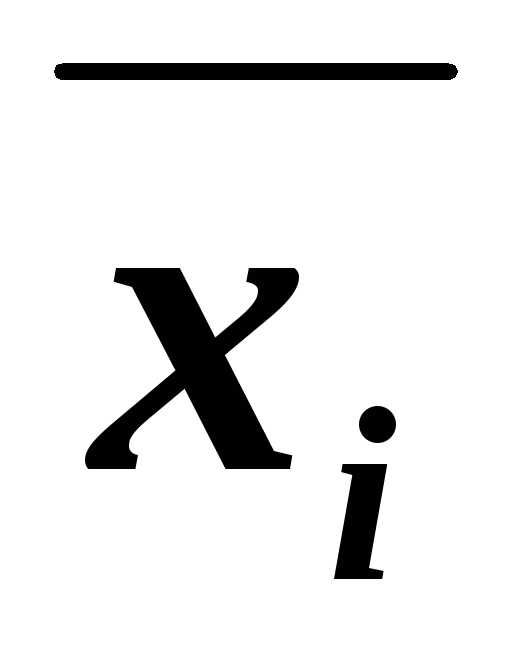 )~
~(Вхi)&(B
)~
~(Вхi)&(B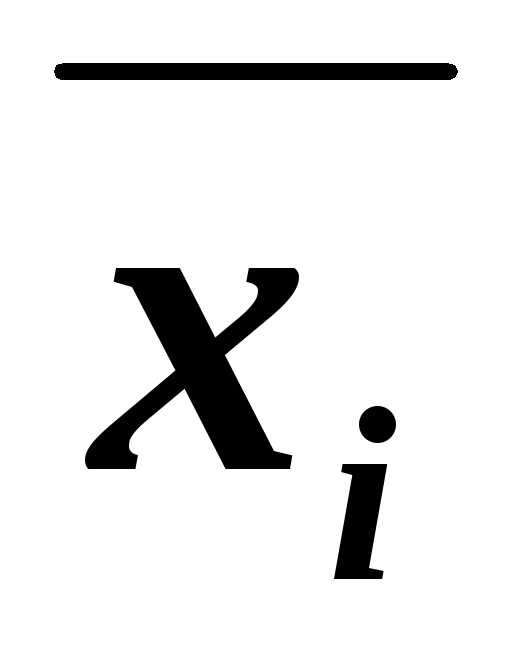 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B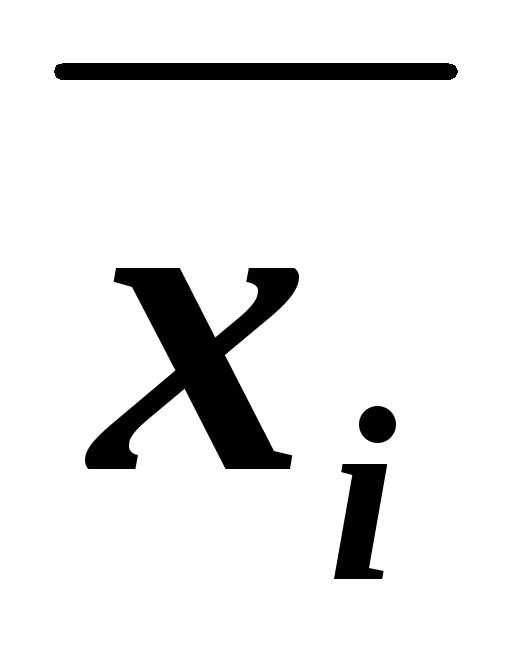 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание 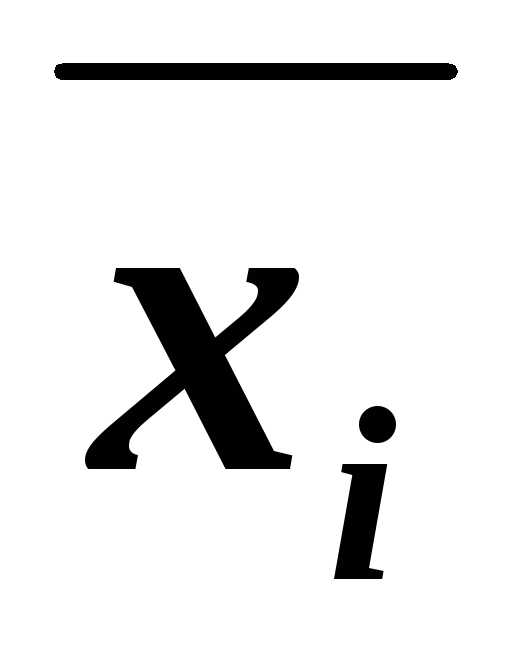 .
.
2. Если в КНФА входят два или более одинаковых дизъюнкта B, то лишние отбрасываем, пользуясь равносильностью B&B&…&B~B.
3. Если некоторый
дизъюнкт В,
входящий в КНФА,
содержит переменную хi и её отрицание 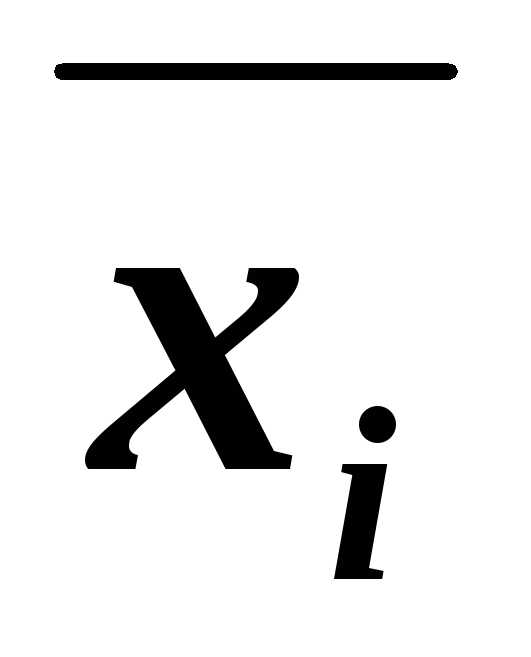 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
4. Если некоторый
дизъюнкт, входящий в КНФА,
содержит одну и ту же литеру 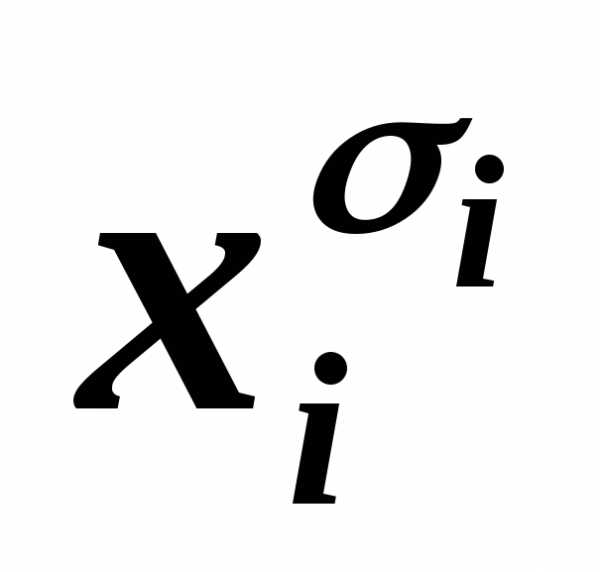 дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью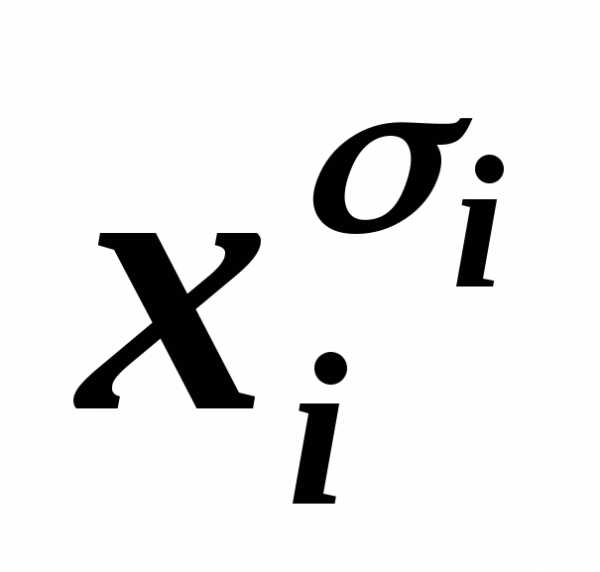
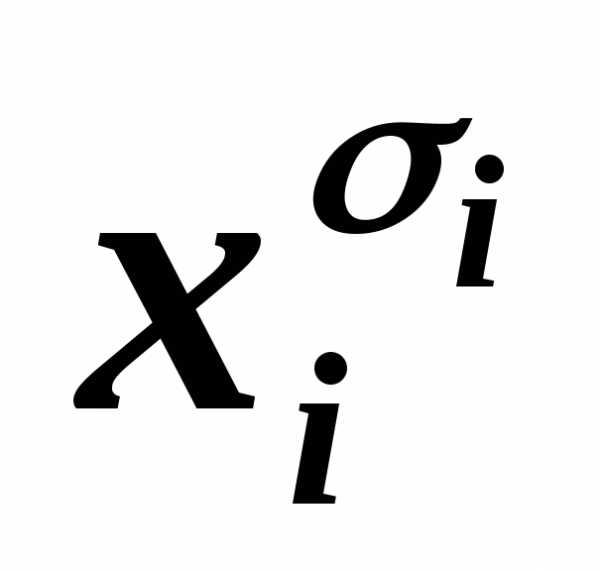 …
…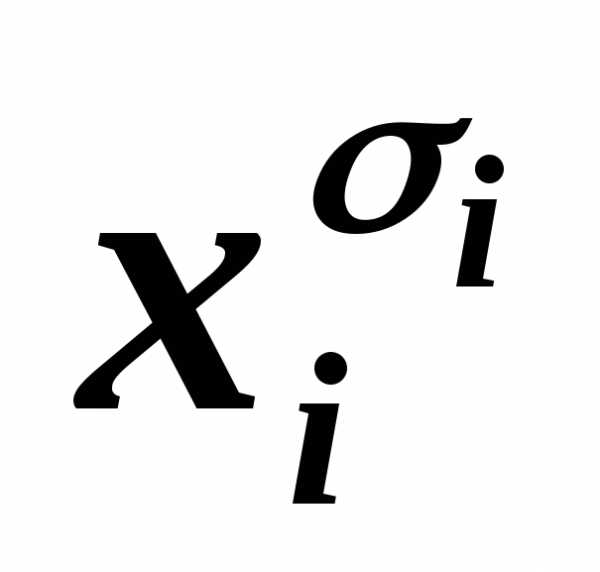 ~
~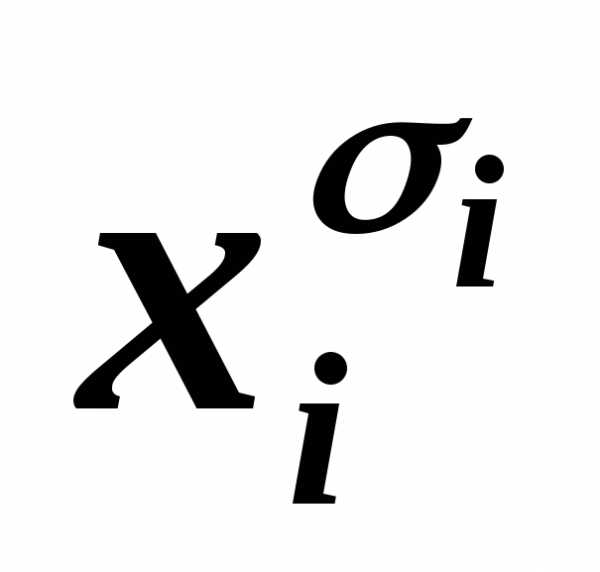 ,
лишние отбрасываем.
,
лишние отбрасываем.
Упражнение 4.3.С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СКНФ.
Решение. з) Приведём формулу к КНФ:
(x| )(z
)(z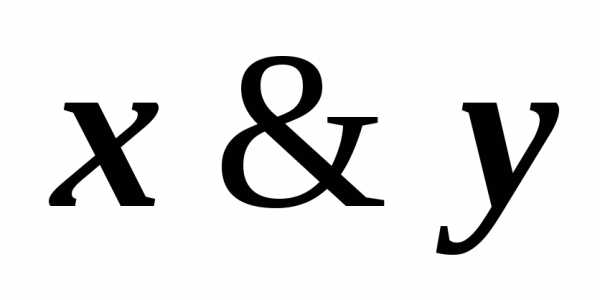 )
)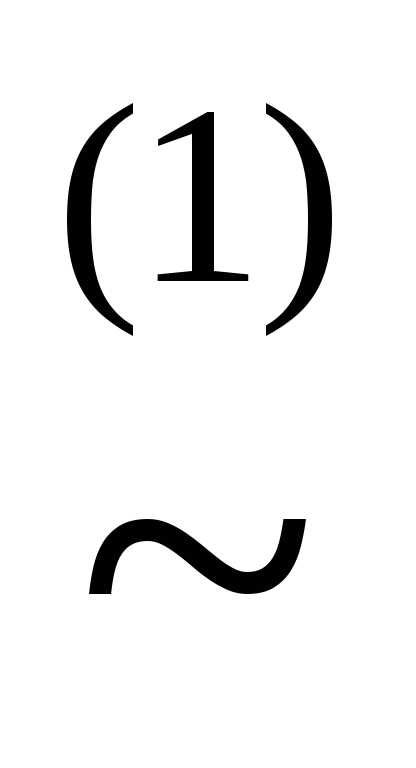 (
(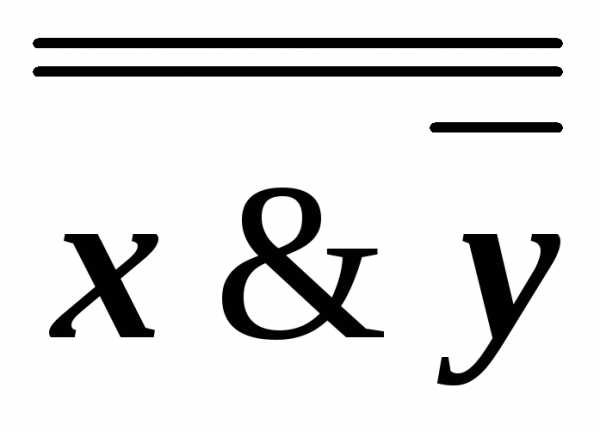 )(z
)(z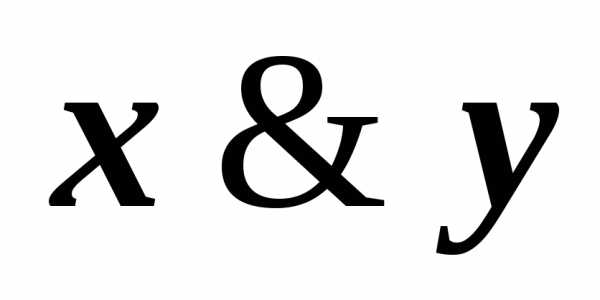 )
)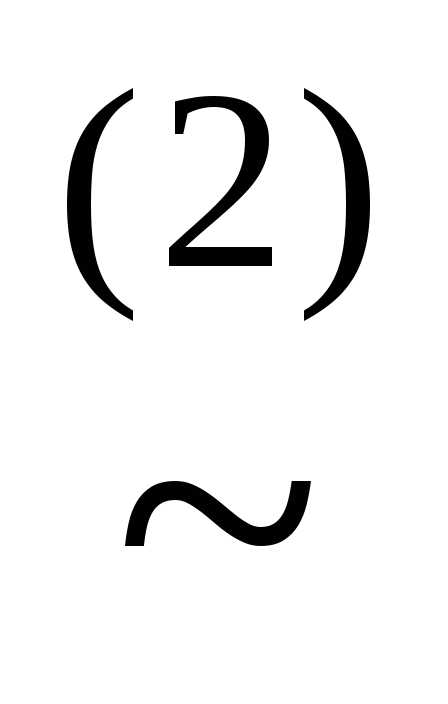 (x&)
(x&)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)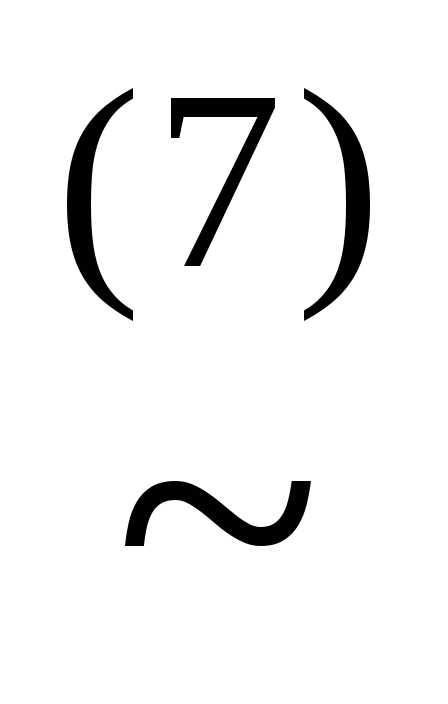
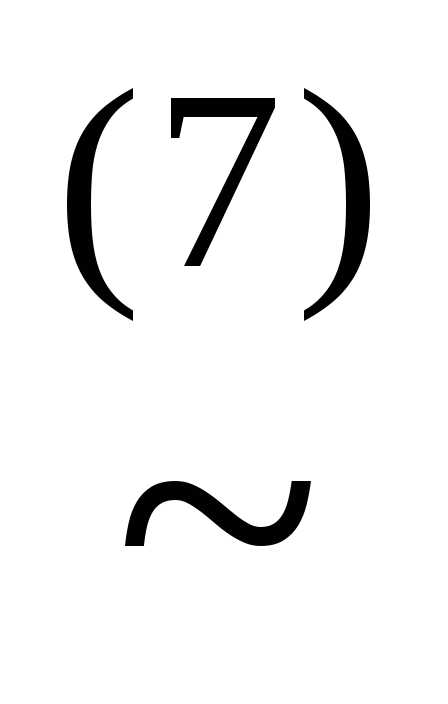 (x&
(x& )(
)( (x&
(x& ))
))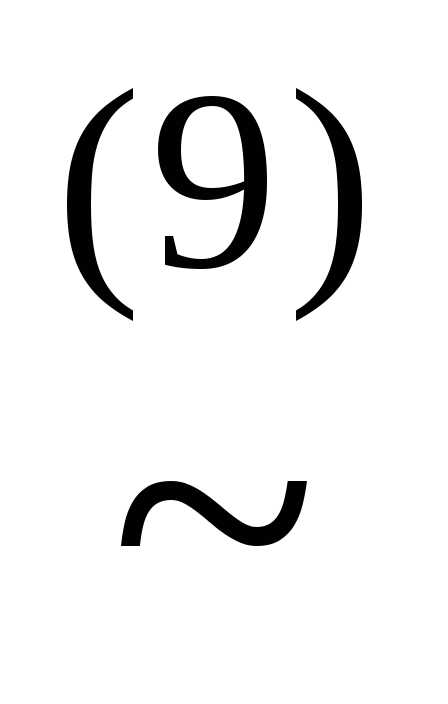
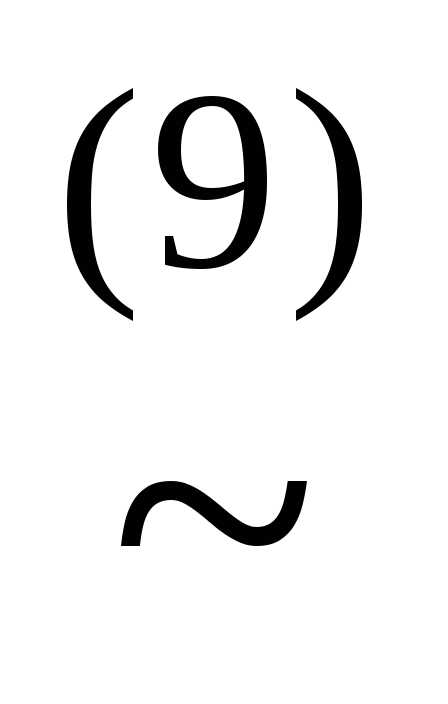 (x&(
(x&(
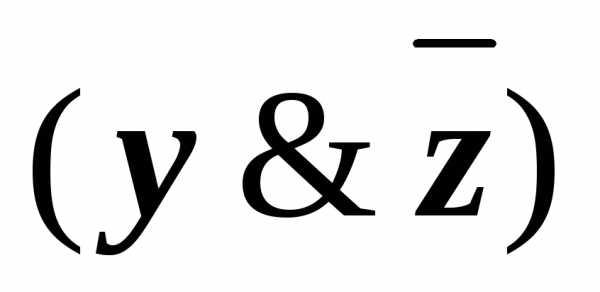 )))
)))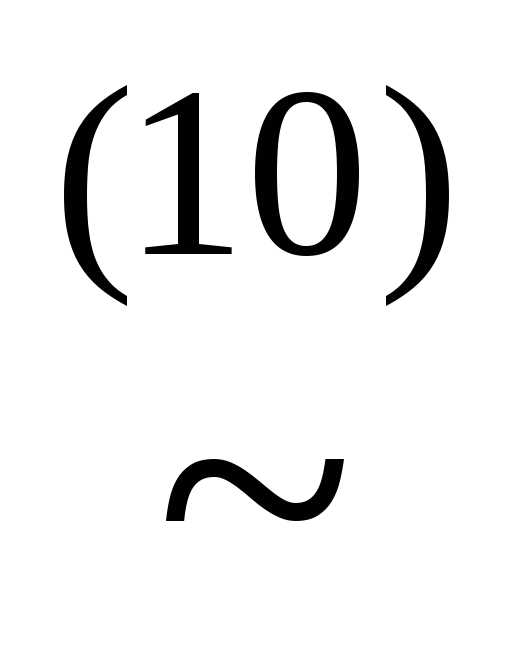 (x&((
(x&(( у)&
у)&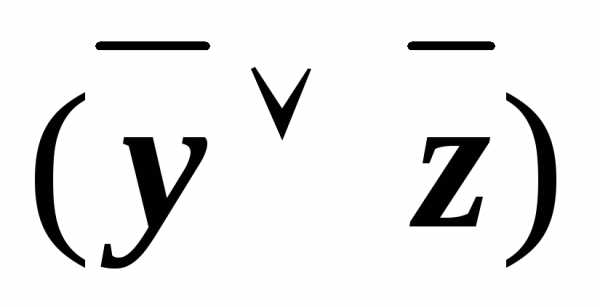 )))
)))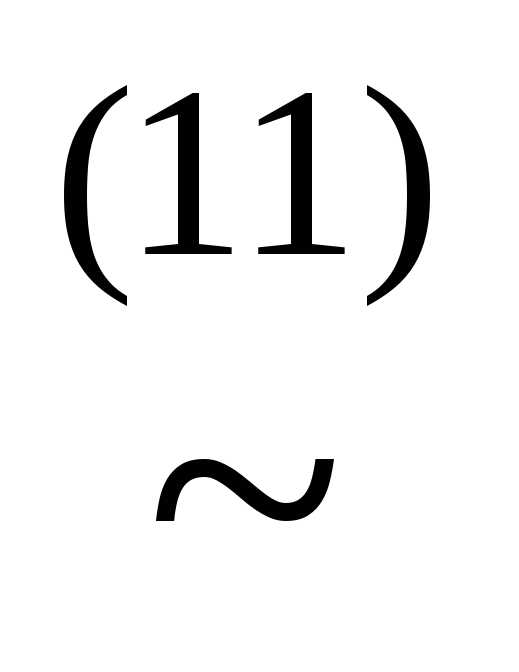
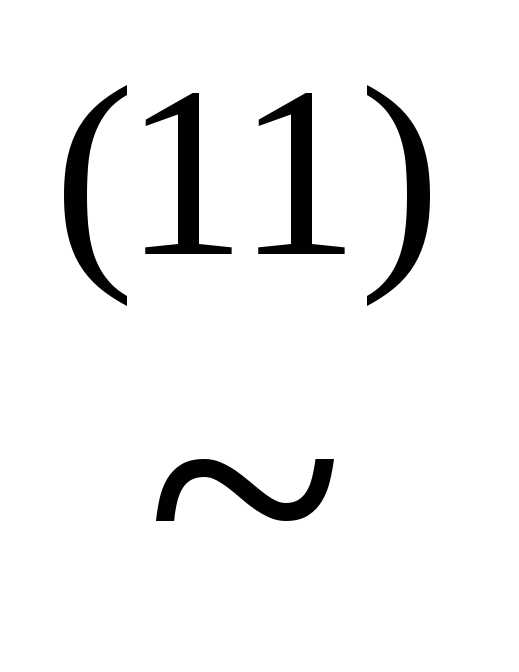 (x&
(x&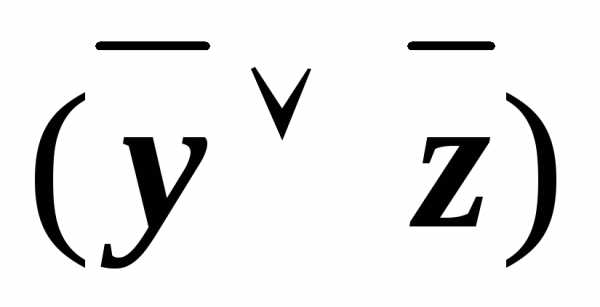 ))
))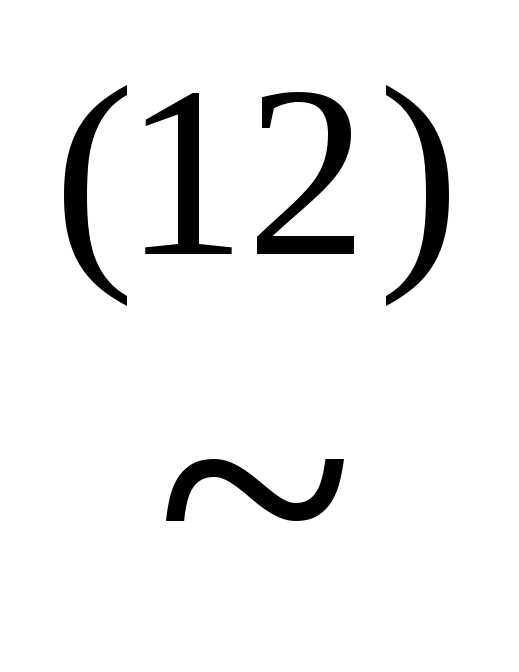 (xz)&
(xz)&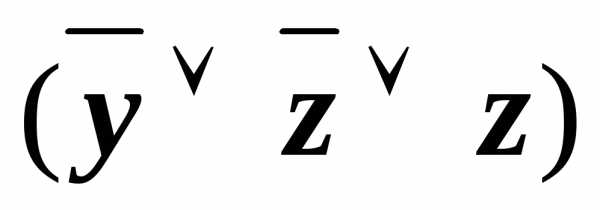 &&
&&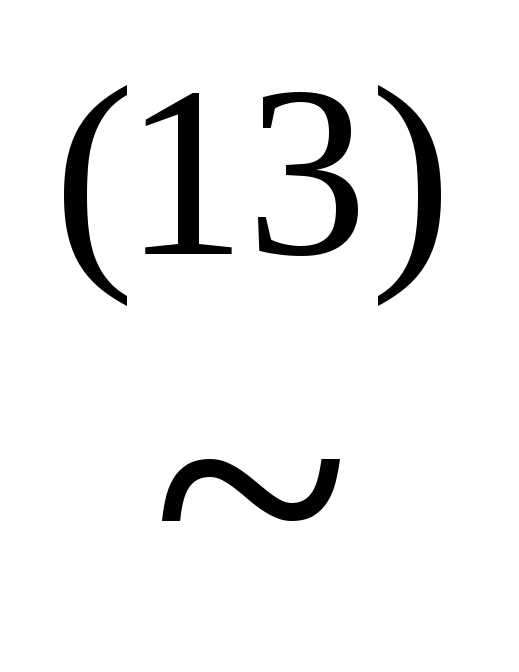
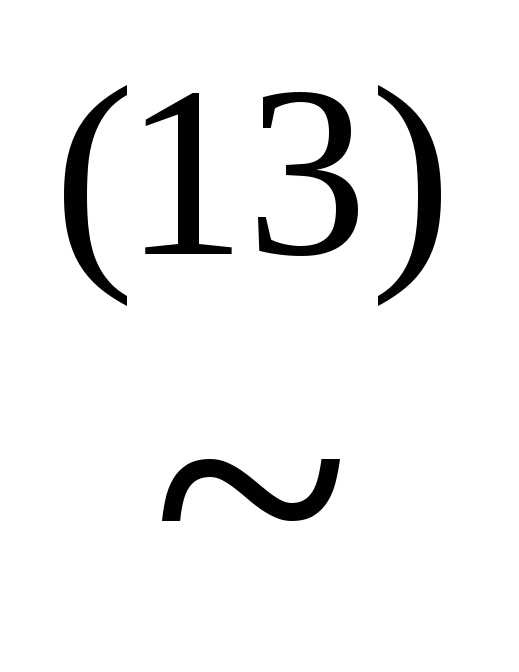 (xz)&
(xz)&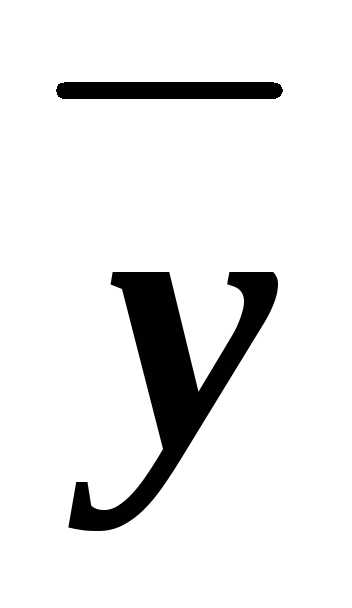 &
&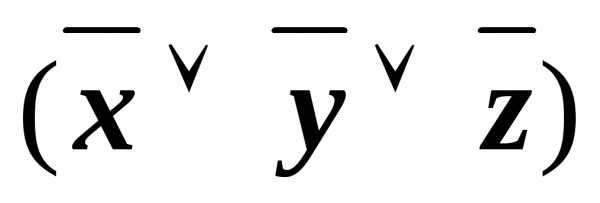
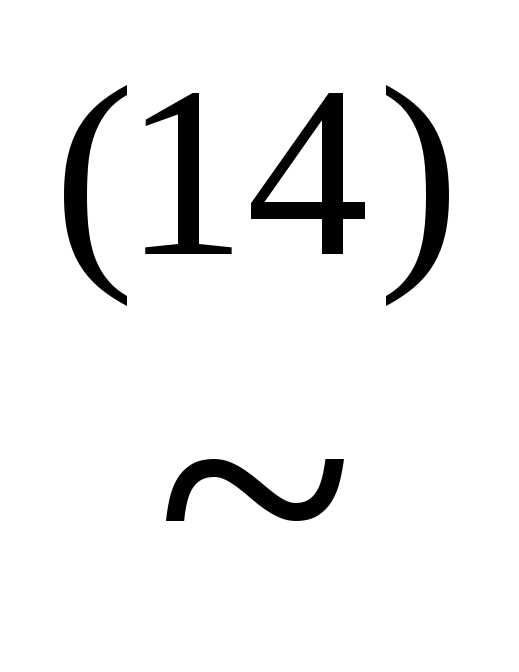
Получили КНФ формулы. Теперь преобразуем КНФ по алгоритму получения всех условий совершенства:
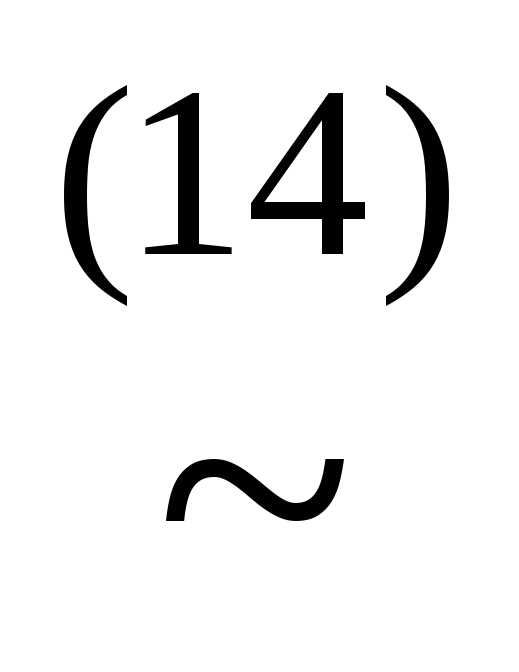 (xyz)&(x
(xyz)&(x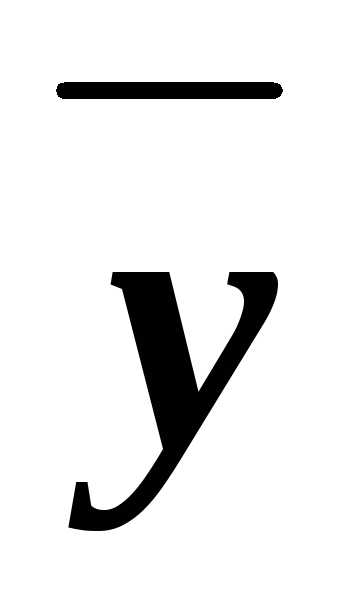 z)&(x
z)&(x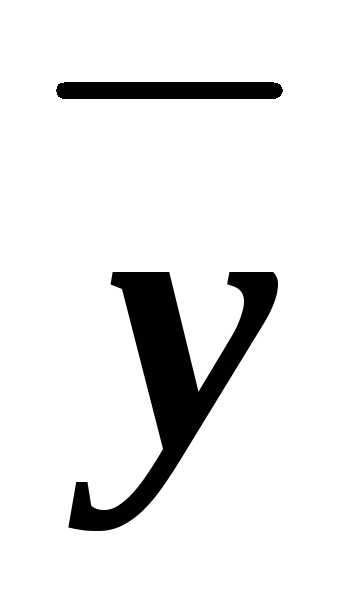 )&
)&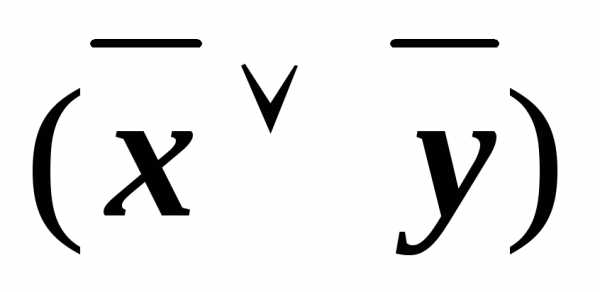 &
&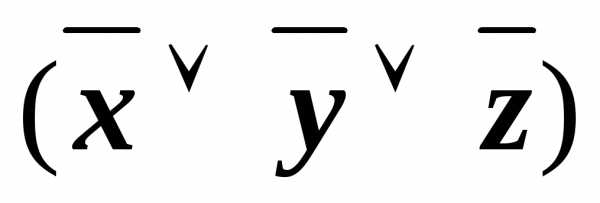

 (xyz)&(x
(xyz)&(x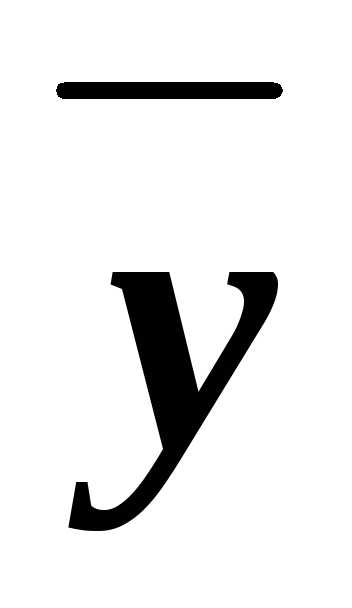 z)&(x
z)&(x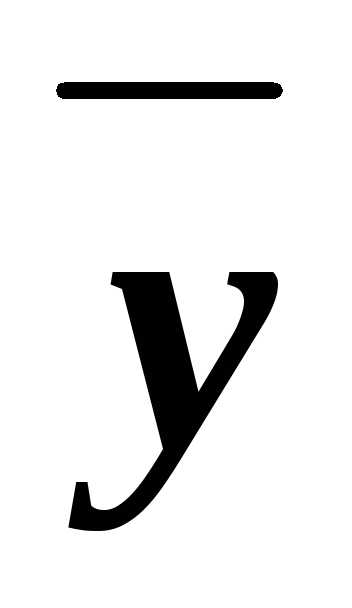 z)&(x
z)&(x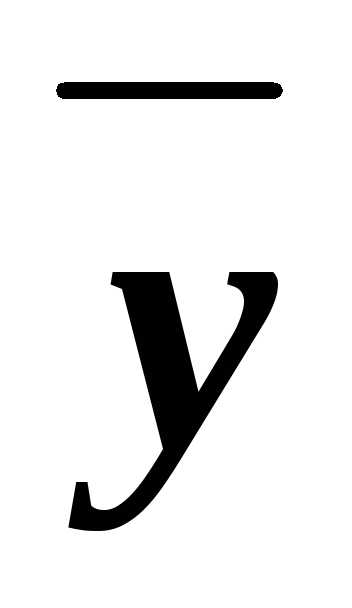
 )&
)&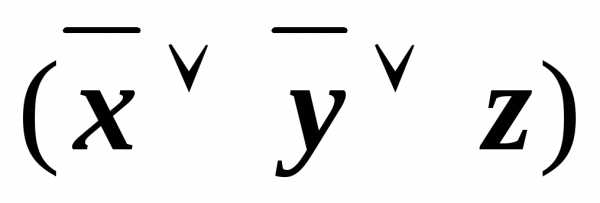 &
&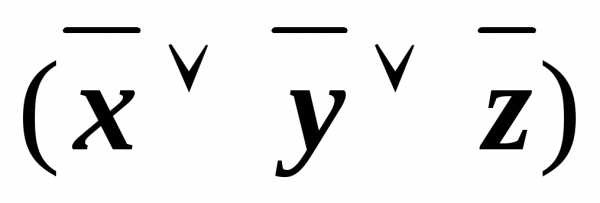 &
&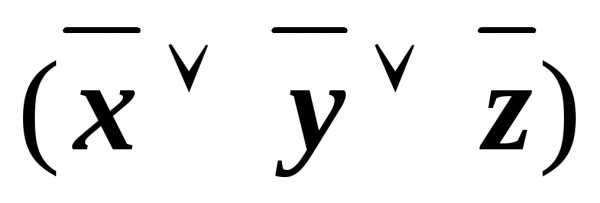
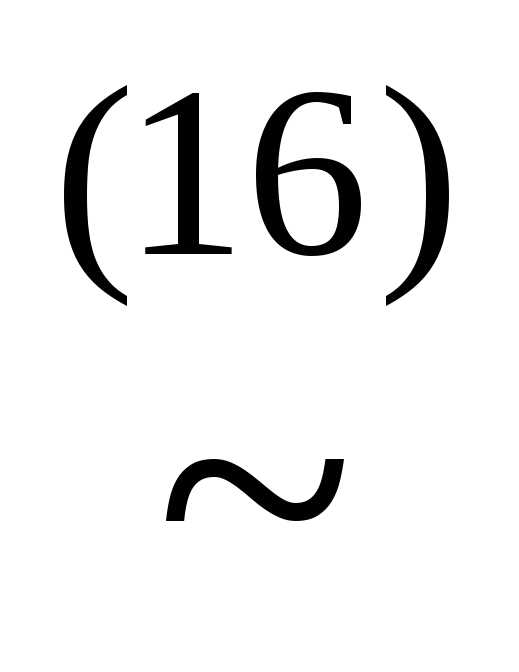
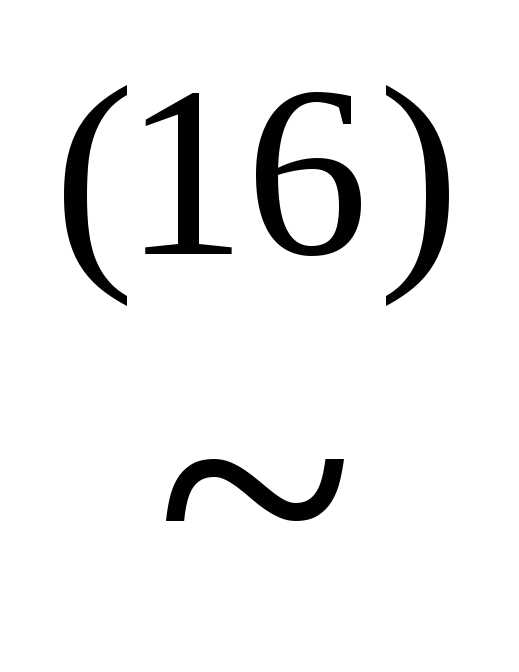 (xyz)&(x
(xyz)&(x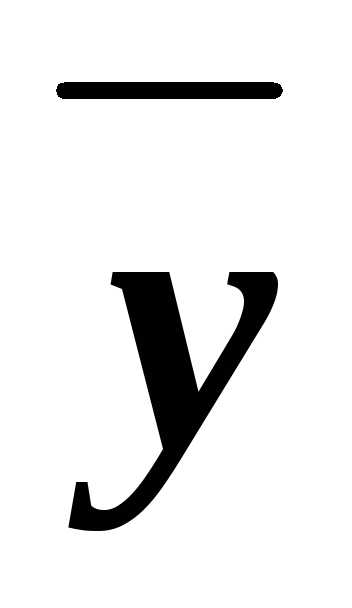 z)&(x
z)&(x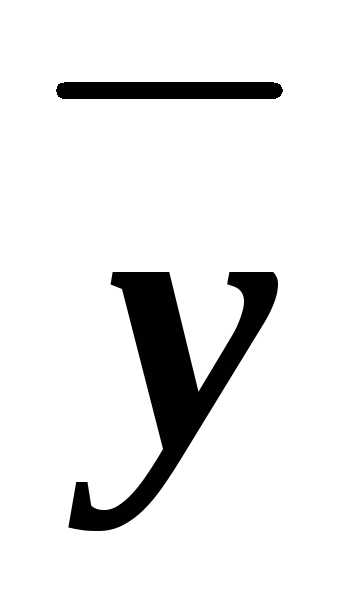
 )&
)&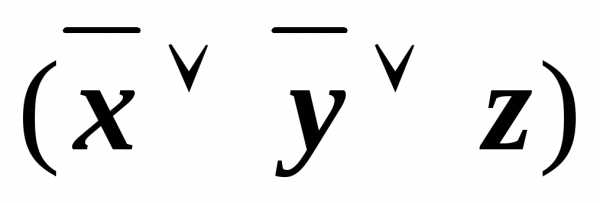 &
&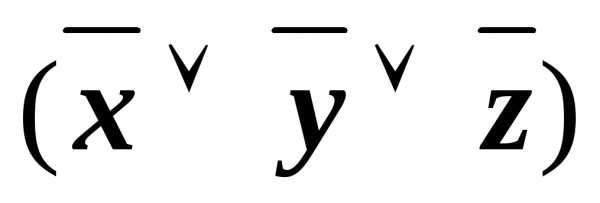
(1) Одновременно заменили | на отрицание операции &,и на отрицание.
(2) Одновременно применили закон двойного отрицания и заменили наи его отрицание.
(3) Операцию заменили на.
(4) Применили закон де Моргана.
(5) Заменили на.
(6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания.
(8) Воспользовались ассоциативностью и коммутативностью .
(9) 1-й и 2-й конъюнкты объединили в один с помощью дистрибутивности & относительно .
(10) К подформуле 
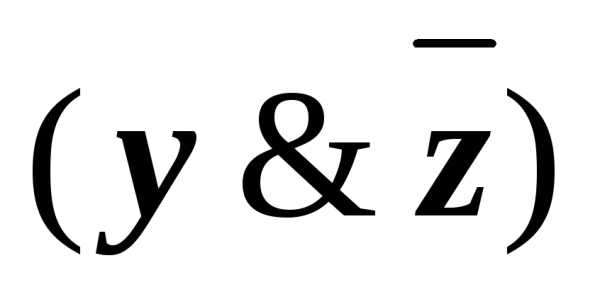 применили закон дистрибутивности.
применили закон дистрибутивности.
(11) Воспользовались тем, что  у~1.
у~1.
(12) Применили сложную дизъюнкцию относительно .
(13) Применили законы исключённого третьего и идемпотентности.
(14) В 1-й и 2-й дизъюнкты добавили недостающие литеры и разбили их по два дизъюнкта каждую (1-я операция приведения к СКНФ).
(15) Операцию, аналогичную (14) проделали с 3-м и 4-м дизъюнктами.
(16) Опустили лишние дизъюнкты.
СДНФ формулы существует и единственна.
Существование СКНФ для любой формулы вытекает из алгоритма её построения.
Другой способ построения СКНФА основывается на следующей эквиваленции:
A(х1, х2,
…, хn)~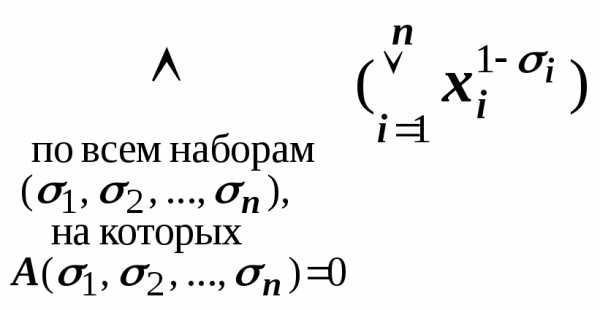 .
.
Другими словами,
формула A(х1, х2,
…, хn)
в своей СДНФ содержит те и только те
конъюнкты вида (4.2), значения которых
равны 0 при xi=1i для всех i=1,
2, …, n.
Например, для формулы А= (
( у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х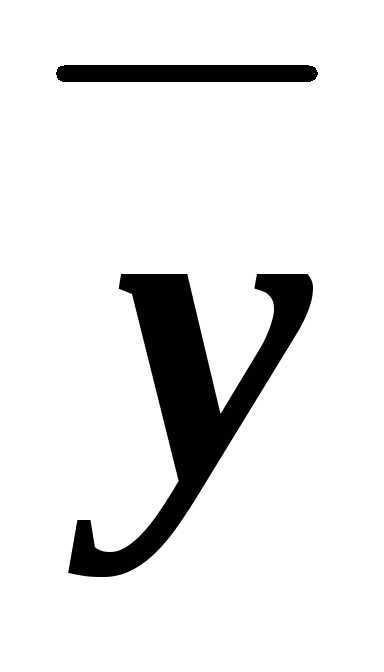 ,
,  у и
у и 
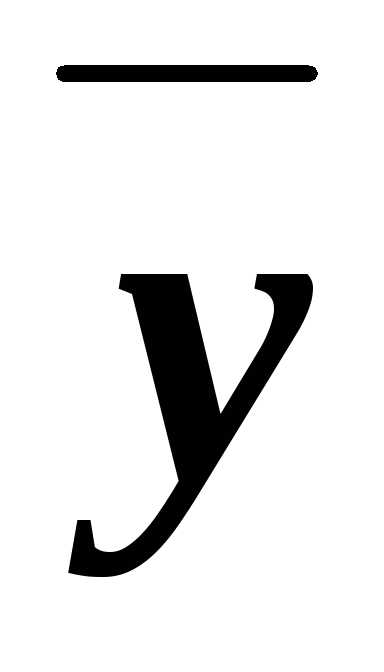 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 
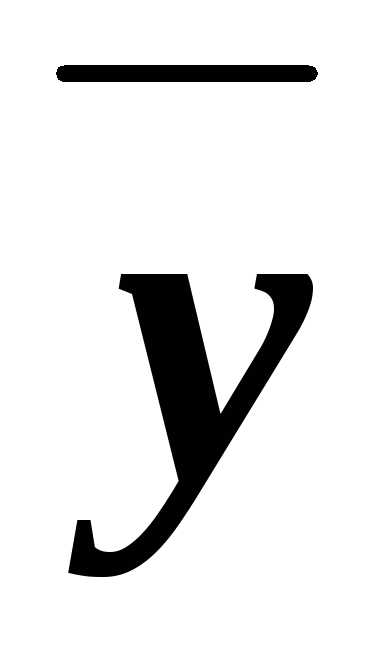 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
Таким образом,
СКНФA(х1, х2,
…, хn)=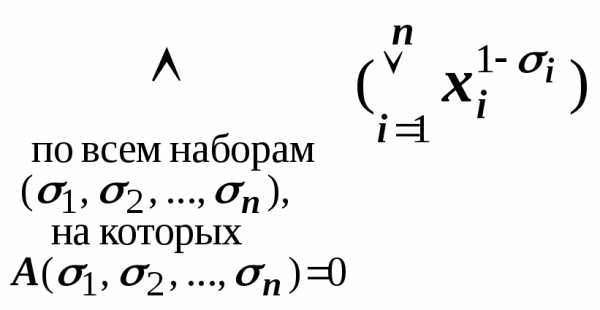 .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
Упражнение 4.4.С помощью таблиц истинности привести формулы упражнения 3.4 к СКНФ.
Решение. д). 1. Составим таблицу истинности формулы (она у нас уже составлена, см. решение задачи д) упражнения 4.2):
2. Выберем те наборы значений переменных, при которых формула принимает значение 0: (0, 0, 1), (0, 1, 1).
3. Составим соответствующие им дизъюнкты: xy ,x
,x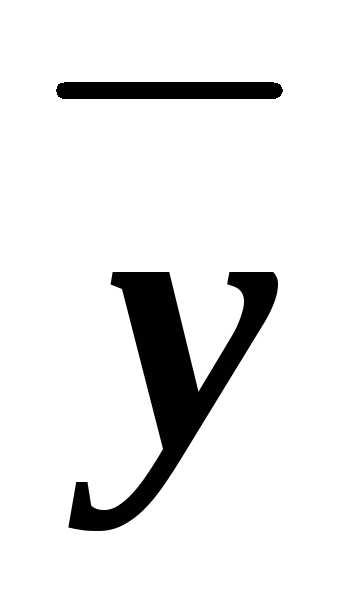
 .
.
4. Составим из них КНФ: (xy )&(x
)&(x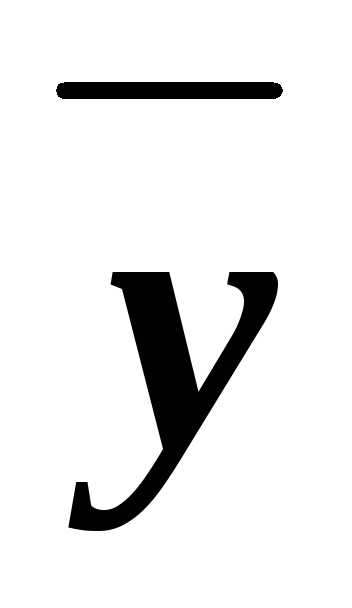
 ).
).
Ответ: д)
СКНФA=(xy )&(x
)&(x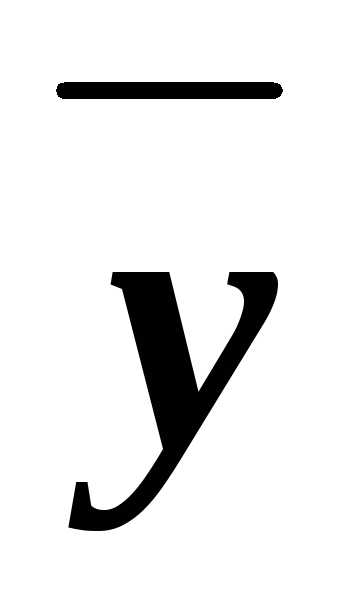
 ).
).
4.3. Принцип двойственности. Операция & называется двойственной к , двойственной к &. Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.
Определение 8. Формула A* называется двойственной к А, если A* получается из A заменой в ней каждой операции на двойственную.
Очевидно, если A* двойственна к A, то A двойственна к A*. Поэтому говорят о взаимно двойственных формулах.
Очевидно также, что если формулы А и В равносильны, то равносильны и двойственные им А* и В*. Кроме того, если A*(х1, х2, …, хп) двойственна к A(х1, х2, …, хп), то ~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.
Определение 9. Формула А называется самодвойственной, если A*~A.
Из определения следует, что формула A самодвойственна, если при замене 0 на 1, и 1 на 0 её таблица истинности не меняется (естественно, меняются между собой только строки). Очевидно, формула самодвойственна тогда и только тогда, когда на всех противоположных значениях переменных формула принимает противоположные значения.
studfiles.net


