Расстояние между точками в координатах – Расстояние между двумя точками | Формулы и расчеты онлайн

alexxlab / / Школьная жизнь

Содержание

формулы, примеры, решения, формула расстояния между двумя точками

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Yandex.RTB R-A-339285-1 Определение 1

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.

К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.

Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.

Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна  11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А бол

zaochnik.com

Расстояние между двумя точками.

Навигация по странице:

Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.


Формулы вычисления расстояния между двумя точками:


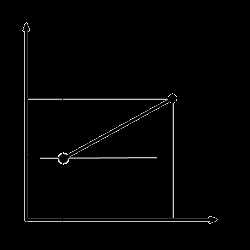
Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = xb — xa;
BC = yb — ya.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC2 + BC2.

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Примеры задач на вычисление расстояния между двумя точками

Пример вычисления расстояния между двумя точками на плоскости

Пример 1.

Найти расстояние между точками A(-1, 3) и B(6,2).

Решение.

AB = √(xb — xa)2 + (yb — ya)2 = √(6 — (-1))2 + (2 — 3)2 = √72 + 12 = √50 = 5√2

Ответ: AB = 5√2.


Пример вычисления расстояния между двумя точками в пространстве

Пример 2.

Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).

Решение.

AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 =

= √(6 — (-1))2 + (2 — 3)2 + (-2 — 3)2 = √72 + 12 + 52 = √75 = 5√3

Ответ: AB = 5√3.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Формула расстояния между точками | Треугольники

Формула для нахождения расстояния между двумя точками A(x1;x2) B(x2;y2) на плоскости:

   

Доказательство:

Сначала рассмотрим частные случаи.

1) Если y1=y2,

то

   

 

К этой же формуле придём, если подставим координаты точек A и B в общую формулу:

   

2) Аналогично, если x1=x2:

   

Эту же формулу получим, подставив координаты A и B в общую формулу:

   

3) Если x1=x2 и y1=y2, AB=0. Формула для этого случая также верна.

4) Если x1≠x2, y1≠y2.

Проведём через точки A и B прямые, перпендикулярные координатным осям. Обозначим точку пересечения этих прямых через C.

Из прямоугольного треугольника ABC по теореме Пифагора

   

Поскольку

   

   

или

   

Отсюда

   

Что и требовалось доказать.

www.treugolniki.ru

Онлайн расчет расстояния по координатам + формула

Расчет расстояния между координатами

Данный сервис позволяет рассчитать расстояние между двумя точками с известными географическими координатами.

Как известно, кратчайшим расстоянием между двумя точками на земной поверхности является длина дуги круга, проведенного на сфере по этим двум точкам. При расчете расстояния по географическим координатам делается предположение, что Земля не плоская, а круглая (если быть точнее, имеет форму, приближенную к сфере), то есть Земля — сфероид.

Для определения расстояния между двумя точками будет применяться формула расчета длины дуги, так называемая «модифицированная формула гаверсинусов».

Поскольку в расчете участвует радиус, а у Земли, как у не совсем правильной сферы, он разный, скажем на северном полюсе — 6335.437 км, а на экваторе — 6399.592 км. В связи с этим в расчете берется среднее значение радиуса Земли равное 6372.795 км, что позволяет получать результат с точность 99,5%.

В калькуляторе ниже для примера приводится расчет расстояния между координатами г.Москва и г.Санкт-Петербург.

Формула расчета расстояния по координатам

Пусть и являются географическими широтой и долготой двух точек 1 и 2, и — их абсолютная разность. Тогда , центральный угол между ними, определяется теоремой сферических косинусов:

Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах

Больше матиматики …

На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния

Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.

Более подробную информацию о выведении формулы расчета расстояния по координатам читайте здесь: http://en.wikipedia.org/wiki/Great_circle_distance

Комментарии:

mapgroup.com.ua

Расстояние между двумя точками.

Расстояние между двумя точками

— это длина отрезка, что соединяет эти точки.


Формулы вычисления расстояния между двумя точками:

  • Формула вычисления расстояния между двумя точками A(

    xa

    , 

    ya

    ) и B(

    xb

    , 

    yb

    ) на плоскости:AB = √
  • Формула вычисления расстояния между двумя точками A(

    xa

    , 

    ya

    , 

    za

    ) и B(

    xb

    , 

    yb

    , 

    zb

    ) в пространстве:AB = √(

    xb

    —

    xa

    )2 + (

    yb

    —

    ya

    )2 + (

    zb

    —

    za

    )2

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC =

xb — xb

;
BC =

y

b — yb

.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √

AC2 + BC2

.

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.


Пример вычисления расстояния между двумя точками на плоскости

Пример 1. Найти расстояние между точками A(-1, 3) и B(6,2).

Решение.

AB = √ = √

(6 — (-1))2 + (2 — 3)2

= √

72 + 12

= √

50

= 5√

2

Ответ: AB = 5√

2

.

Пример вычисления расстояния между двумя точками в пространстве

Пример 2. Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).

Решение.

AB = √(

xb

—

xa

)2 + (

yb

—

ya

)2 + (

zb

—

za

)2
=

= √

(6 — (-1))2 + (2 — 3)2 + (-2 — 3)2

= √

72 + 12 + 52

= √

75

= 5√

3

Ответ: AB = 5√

3

.

o-math.com

Расстояние между двумя точками на прямой

Расстояние между двумя точками на координатной прямой равно модулю разности их координат.

Формула расстояния между точками на координатной прямой:

AB = |a — b|

где A и B – это произвольные точки, расстояние между которыми надо найти, то есть найти длину отрезка AB, a и b – координаты точек.

Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.

Следовательно,

чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.

Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:

|-3 — 5| = |-8| = 8   или   |5 — (-3)| = |5 + 3| = 8

Ответ. Расстояние между точками L и M равно 8.

Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).

Решение. Обозначим середину отрезка точкой C. Так как C – середина отрезка AB, то |AC| = |CB|, значит чтобы найти координату точки C надо сначала вычислить длину отрезка AB и разделить её на 2, то есть на две равные части AC и CB:

AB = |-5 — 5| = |-10| = 10

10 : 2 = 5,   значит   |AC| = |CB| = 5

Как видно из чертежа, чтобы найти координату середины отрезка надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:

-5 + 5 = 0   или   5 — 5 = 0

Ответ. Координата середины отрезка C(0).

Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).

Решение.

AB = |7 — 25| = |-18| = 18

AC = CB = 18 : 2 = 9

7 + 9 = 16   или   25 — 9 = 16

Ответ. Координата точки C – 16.

naobumium.info

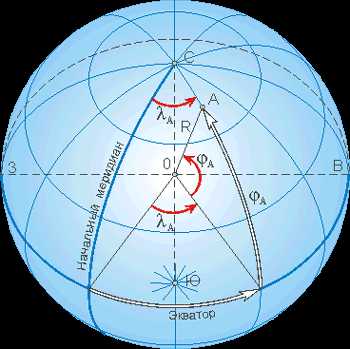
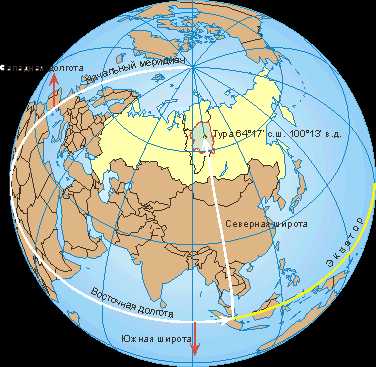
Определение расстояний на поверхности Земли


Определение расстояний на поверхности Земли

Размеры и форма Земли
Форма Земли отличается от шара и имеет несколько сплющенную форму, близкую к сфероиду (эллипсоиду вращения), но истинная фигура Земли отличается и от сфероида, и от трехосного эллипсоида и не может быть представлена ни одной из известных математических фигур.
Поэтому, говоря о фигуре Земли, имеют в виду не физическую форму земной поверхности, с океанами и материками, с их возвышенностями и впадинами, а так называемую поверхность геоида.

Поверхность, нормалями к которой в любой из ее точек являются отвесные линии, называется уровенной поверхностью, или поверхностью равновесия. Уровенных поверхностей, как внутри Земли, так и охватывающих земную поверхность, или пересекающихся с ней, можно провести бесчисленное множество.
Та поверхность равновесия, которая совпадает в открытом океане с поверхностью покоящейся свободной воды, называется геоидом.

Для решения многих задач навигации и составления карт мелкого масштаба Землю принимают за сферу (шар).
Положение точки па земной сфере определяется сферическими координатами: сферической широтой и сферической долготой (в картографии применяют термин «географические координаты«).
Сферическая широта точки А — угол φА между плоскостью экватора и направлением R на данную точку из центра земной сферы.
Сферическая долгота точки А — угол λА, заключенный между плоскостью нулевого (Гринвичского) меридиана и плоскостью меридиана данной точки.

Средний радиус Земли R = 6371210 м.
Экваториальный радиус Земли RЭ = 6378,245 м.
Полярный радиус Земли RП = 6356,830 м.
Длина дуги меридиана (дуги экватора, дуги окружности большого круга) в 1°, 1′ и 1″ равна соответственно:
111 197 м (111,2 км), 1852 м (1,852 км) и 30,9 м.

 

 

Законы сферической тригонометрии позволяют рассчитывать расстояния между точками, расположенными на сфере.
Кратчайшее расстояние между двумя точками на земной поверхности (если принять ее за сферу) определяется зависимостью:

cos(d) = sin(φА)·sin(φB) + cos(φА)·cos(φB)·cos(λА − λB),

где φА и φB — широты, λА, λB — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара.
Расстояние между пунктами, измеряемое в километрах, определяется по формуле:

L = d·R,

где R = 6371 км — средний радиус земного шара.

 

Таблица расстояний (с точностью 1 км), рассчитанными по этим формулам,
для пунктов Эвенкийского автономного округа (Эвенкийского муниципального района):

 

уточнения внесены 25.03.2010 Тура Байкит Ванавара
Красноярск 1007 662 738
Агата 426    
Географический центр РФ, Виви 364    
Ессей 467    
Кислокан 201    
Нидым 21    
Ногинск 439    
Тембенчи 99    
Тура   350 450
Тутончаны 313    
Учами 186    
Чиринда 363    
Эконда 293    
Юкта  293    
Байкит  350   352
Бурный   197  
Кузьмовка   236  
Куюмба   82  
Мирюга   220  
Ошарово   177  
Полигус   101  
Суломай   274  
Суринда   114  
Таимба   203  
Усть-Камо    121  
Ванавара 450 352  
Кербо     242
Муторай     147
Оскоба     100
Стрелка-Чуня     159
Тунгусский метеорит (эпицентр)     64
Чемдальск     102

Для расчета расстояния между пунктами, расположенными в разных полушариях (северное-южное, восточное-западное), знаки (±) у соответствующих параметров (широт или долгот) должны быть разными.

Пример: (см. таблицу ниже)
для вычисления расстояния между Турой и Сиднеем (Австралия) применяем формулу:
cos(d) = sin(φА)·sin(−φB) + cos(φА)·cos(−φB)·cos(λА − λB) = −0,27462.

d = 1,848988
Расстояние L = d·R = 11 779,9 км.

для вычисления расстояния между Турой и Нью-Йорком (США) применяем формулу:
cos(d) = sin(φА)·sin(φB) + cos(φА)·cos(φB)·cos(λА + λB) = 0,259532.

d = 1,308259

Расстояние L = d·R = 8 334,92 км.

В таблице расстояния определены с точностью 1 км.

φ (градус)

λ (градус)

φ (радиан)

λ (радиан)

расстояние до Туры (км)

Тура
Tura (Russia)

64,28 с.ш.

100,22 в.д.

1,121387

1,748224

— 

Нью-Йорк (США)
New-York (USA)

40,71 с.ш.

74,01 з.д.

0,710163

1,291063

8 335

Сидней (Австралия)
Sydney (Australia)

33,874 ю.ш.

151,213 в.д.

0,590913

2,637827

11 780

Координаты географических пунктов ЭАО смотрите здесь

страница обновлена 25.03.10

osiktakan.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *