Посчитать среднее арифметическое онлайн – Среднее арифметическое | Формулы и расчеты онлайн

Как посчитать среднее значение 🚩 Найти среднее арифметическое всех целых чисел от 1 до 1000 🚩 Математика

22 июля 2011

Автор КакПросто!

В математике и статистике среднее арифметическое (или просто среднее) набора чисел — это сумма всех чисел в этом наборе, поделённая на их количество. Среднее арифметическое является наиболее общим и самым распространённым понятием средней величины.

Вам понадобится

• Знания по математике.

Инструкция

Пусть дан набор из четырех чисел. Необходимо найти среднее значение этого набора. Для этого сначала найдем сумму всех этих чисел. Допустим эти числа 1, 3, 8, 7. Их сумма равна S = 1 + 3 + 8 + 7 = 19. Набор чисел должен состоять из чисел одного знака, в противном случае смысл в вычислении среднего значения теряется.

Среднее значение набора чисел равно сумме чисел S, деленной на количество этих чисел. То есть получается, что среднее значение равно: 19/4 = 4.75.

Для набора числе также можно найти не только среднее арифметическое, но и среднее геометрическое. Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Среднее геометрическое G ищется по формуле: корень N-ой степени из произведения набора чисел, где N — количество числе в наборе. Рассмотрим тот же набор чисел: 1, 3, 8, 7. Найдем их среднее геометрическое. Для этого посчитаем произведение: 1*3*8*7 = 168. Теперь из числа 168 необходимо извлечь корень 4-ой степени: G = (168)^1/4 = 3.61. Таким образом среднее геометрическое набора чисел равно 3.61.

Обратите внимание

Среднее значение не может быть больше самого большого числа в наборе и меньше самого маленького.

Полезный совет

В математической статистике среднее значение величины называется математическим ожиданием.

Источники:

• как вычислить среднее значение
• Найти среднее арифметическое всех целых чисел от 1 до 1000
• [Turbo Pascal] Нахождение среднего геометрического

Ситуация, когда интернет «ползает», словно улитка, — далеко не редкость. И это происходит несмотря на все количество цифр в рекламном буклете вашего провайдера. Обещанная скорость превышает десятки мегабайт в секунду, но на деле нет даже десятой части от обещанного. Если вы хотите измерить настоящую, а не рекламную скорость вашего соединения, то эта статья вам поможет.

Инструкция

Вот несколько ссылок, пройдя по которым, вы можете измерить скорость своего соединения: speed.yoip.ru; 2ip.ru; www.softholm.com; spchat.ru; www.testinternet.ru; www.and-rey.ru. Также необходимо помнить, что для того, чтобы получить наиболее точный и правильный результат тестирования вам нужно отключить все программы, которые могут использовать интернет в момент проведения тестирования. Это могут быть любые интернет-качалки, интернет-радио или телевидение.

Для измерения «моментальной» скорости вашего соединения с интернетом вам нужно перейти по любой ссылке, приведенной выше и нажать кнопку «Измерить скорость».

В течение нескольких минут вам необходимо воздержаться от использования интернета. Это необходимо для того, чтобы браузер, который вы используете для просмотра интернет-страниц, не влиял на скорость соединения.

В таблице, которая появится после завершения тестирования, вы увидите скорость вашего соединения с интернетом.

Видео по теме

Обратите внимание

Необходимо помнить, что тест для измерения скорости показывает не среднюю скорость загрузки пакета и не максимальную скорость, с которой может работать ваш интернет, а именно скорость передачи в данный момент времени. На результат теста оказывает влияние размера пакета передаваемых данных. Здесь действует правило: чем больший объем пакета, тем более точные результаты тестирования.

Полезный совет

Измерение скорости осуществляется путем расчета времени передачи какого-либо объема данных с сервера. Объем данных для передачи имеет определенное значение. Если рассчитанная скорость не соответствует ожидаемой или обещанной провайдером, тогда попробуйте повторить тестирование спустя некоторое время. Вполне возможно, что канал вашего провайдера сильно перегружен.

Среднее арифметическое, которое иногда называют просто средним, – одно из важных понятий в математике и статистике. Среднее арифметическое любого набора величин находится при помощи двух последовательных операций, производимых при помощи калькулятора.

Вам понадобится

Инструкция

Для начала сложите все числа из того набора, для которого нужно найти среднее арифметическое. Например, вам дана последовательность из пяти чисел: 8, 17, 22, 14 и 29. В этом случае первым шагом в расчете среднего арифметического будет нахождение суммы этих чисел: 8 + 17 + 22 + 14 + 29 = 90.

Теперь, когда сумма найдена, разделите ее на количество суммированных чисел. В нашем наборе было 5 чисел, поэтому мы разделим 90 на 5. 90 : 5 = 18. Полученное число и будет являться средним арифметическим исходного набора чисел.

Видео по теме

Обратите внимание

Среднее арифметическое призвано описывать центральную тенденцию, однако, иногда этому мешает влияние «больших отклонений». Например, среднее арифметическое для набора чисел 2, 1, 1, 2, 1, 11 будет равняться трем, тогда как большинство элементов ряда (пять из шести) явно ниже этого значения.

Источники:

• Онлайн-калькулятор, рассчитывающий среднее арифметическое

Числовая характеристика множества функций или чисел, заключенная между максимальным и минимальным значениями, называется средним значением. В математике под этим определением можно понимать среднее значение функции, среднее взвешенное, среднее хронологическое. В теории вероятностей и статистике — это непараметрические средние, такие как мода, медиана и среднее значение случайной величины. Для каждого из этих понятий существует свой алгоритм расчета.

Вам понадобится

• Учебники по высшей математике, теории вероятности, статистике

Инструкция

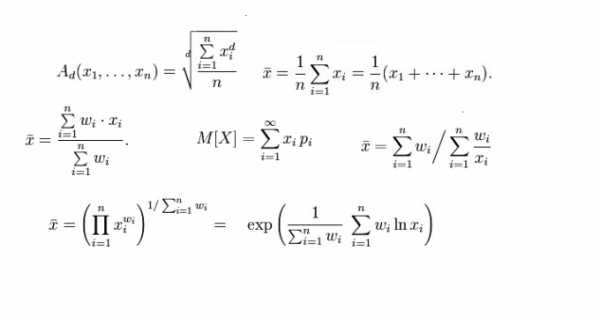
Итак, в математике наиболее распространен и востребован расчет среднего степенного значения функции по Колмогорову. Частными случаями Колмогоровских средних являются среднее арифметическое, среднее квадратичное, среднее гармоническое, среднее геометрическое. Для расчета среднего арифметического значения (или простого среднего), просуммируйте весь ряд чисел и поделите на их количество. Вычислите квадратный корень из среднего арифметического квадратов данных чисел, и вы получите среднее квадратичное значение. Среднее гармоническое и среднее геометрическое также несложно вычислить, путем подстановки ряда данных в формулы Среднее взвешенное значение вычисляется, когда мы имеем дело с линейными комбинациями. Тут тоже существуют различные алгоритмы. Чаще всего используют среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное. Эти величины вы можете вычислить, воспользовавшись следующими формулами:

Хронологическое среднее используется для вычисления среднего значения абсолютных величин, меняющихся в определенном временном интервале. Для вычисления этого значения используйте данную формулу:

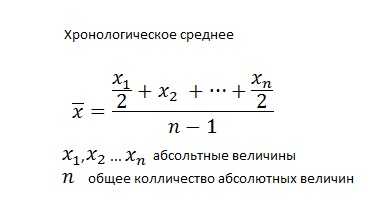
В статистике наиболее часто встречаются такие понятия как мода и медиана. Они являются непараметрическими средними. Напомним что мода — это наиболее часто встречающееся число в данном ряде, а медиана — некоторое значение признака, которое будет делить весь ряд выборки на две равные части «верхние» и «нижние».

В теории вероятности среднее значение случайной величины не что иное как математическое ожидание. Если у вас дискретное распределение, то математическое ожидание вычисляется по формуле (1), а если непрерывное, но по формуле (2)

Источники:

• среднее взвешенное значение

Средние величины играют огромную роль в нашей жизни. Они применяются повсюду, начиная от беспристрастной статистики и экономической теории и заканчивая подсчетом балов в КВН.

Вам понадобится

Инструкция

Средняя величина — это показатель однородной совокупности, который нивелирует индивидуальные различия значений статистических величин, тем самым давая обобщающую характеристику варьирующего признака. Средняя величина показывает характеристику всей совокупности в целом, а не ее отдельных величин. Средняя величина несет в себе то общее, что присуще всем элементам совокупности. Для применения средних величин должны соблюдаться два условия. Первое условие – однородность совокупности. Второе условие – достаточно большой объем совокупности, для которой рассчитывается средняя. Средняя арифметическая — самая простая и часто используемая величина. Формула для нахождения ее имеет следующий вид:

Xсред. = ∑x/n

Где x — само значение величин, а n — общее количество значений величин.

Бывают случаи, когда использование средней арифметической некорректно для решения поставленной задачи, тогда используются другие средние величины.

Средняя геометрическая в отличии от средней арифметической применяется при определении средних относительных изменений. Геометрическая средняя является более точным результатом осреднения в задачах на вычисление значения X равноудаленного как от минимального, так и от максимального значения величины совокупности.

Формула имеет вид:

X= √(n&x1∙x2∙… ∙Xn)

Среднее квадратичное используется в тех случаях, когда значения совокупности могут быть как положительными величинами, так и отрицательными. Применяется при расчете средних отклонений и измерении вариации значений величины X.

Формула имеет вид:

X= √((x1^2+x2^2+⋯+xn^2)/n)

Видео по теме

Среднее арифметическое — важное понятие, используемое во многих разделах математики и ее приложениях: статистике, теории вероятностей, экономике и.т.д. Среднее арифметическое можно определить как общее понятие средней величины.

Инструкция

Среднее арифметическое набора чисел определяется как их сумма, деленная на их количество. То есть сумма всех чисел набора делится на количество чисел в этом наборе.Наиболее простой случай — найти среднее арифметическое двух чисел x1 и x2. Тогда их среднее арифметическое X = (x1+x2)/2. Например, X = (6+2)/2 = 4 — среднее арифметическое чисел 6 и 2. Общая формула для нахождения среднего арифметического n чисел будет выглядеть так: X = (x1+x2+…+xn)/n. Ее можно также записать в виде: X = (1/n)?xi, где суммирование ведется по индексу i от i = 1 до i = n.К примеру, среднее арифметическое трех чисел X = (x1+x2+x3)/3, пяти чисел — (x1+x2+x3+x4+x5)/5.

Интерес представляет ситуация, когда набор чисел представляет собой члены арифметической прогрессии. Как известно, члены арифметической прогрессии равны a1+(n-1)d, где d — шаг прогрессии, а n — номер члена прогрессии.Пусть a1, a1+d, a1+2d,…, a1+(n-1)d — члены арифметической прогрессии. Их среднее арифметическое равно S = (a1+a1+d+a1+2d+…+a1+(n-1)d)/n = (na1+d+2d+…+(n-1)d)/n = a1+(d+2d+…+(n-2)d+(n-1)d)/n = a1+(d+2d+…+dn-d+dn-2d)/n = a1+(n*d*(n-1)/2)/n = a1+dn/2 = (2a1+d(n-1))/2 = (a1+an)/2. Таким образом среднее арифметическое членов арифметической прогрессии равно среднему арифметическому его первого и последнего членов.

Также справедливо свойство, что каждый член арифметической прогрессии равен среднему арифметическому предыдущего и последующего члена прогрессии: an = (a(n-1)+a(n+1))/2, где a(n-1), an, a(n+1) — идущие друг за другом члены последовательности.

Видео по теме

Обратите внимание

Для нахождения среднего арифметического нескольких чисел следует сложить их между собой. После этого полученную сумму следует разделить на количество слагаемых. Чтобы стало более понятно, давайте вместе разберемся, как найти среднее арифметическое чисел, на примере: 78, 115, 121 и 224.  Среднее арифметическое нескольких чисел: найти с помощью Excel.

Полезный совет

Вычисленное нами значение называется средним арифметическим или просто средним. Определение. Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.  Не только среднее арифметическое показывает, где на числовой прямой располагаются числа какого-либо набора. Другим показателем является медиана — число, которое разделяет этот набор на две части, одинаковые по численности. Поясним на примерах, как найти медианы разных наборов чисел.

Источники:

• как найти среднее арифметическое двух чисел

Среднее значение — это одна из характеристик набора чисел. Представляет собой число, которое не может выходить за пределы диапазона, определяемого наибольшим и наименьшим значениями в этом наборе чисел. Среднее арифметическое значение — наиболее часто используемая разновидность средних.

Инструкция

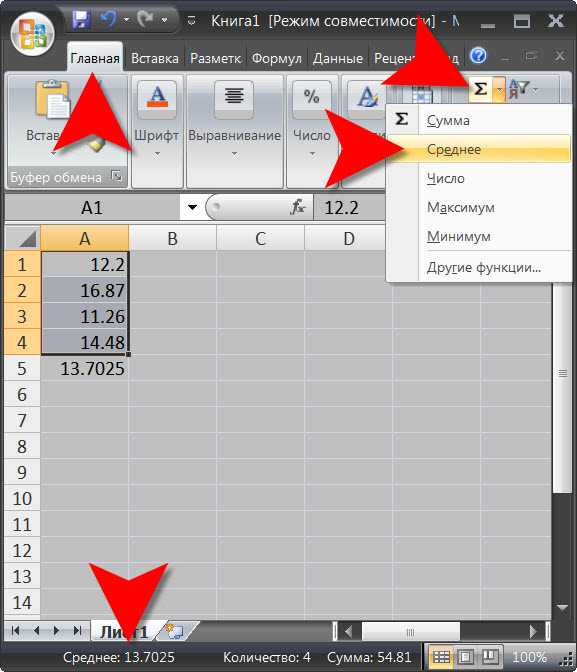
Сложите все числа множества и разделите их на количество слагаемых, чтобы получить среднее арифметическое значение. В зависимости от конкретных условий вычисления иногда бывает проще делить каждое из чисел на количество значений множества и суммировать результат. Используйте, например, входящий в состава ОС Windows калькулятор, если вычислить среднее арифметическое значение в уме не представляется возможным. Открыть его можно с помощью диалога запуска программ. Для этого нажмите «горячие клавиши» WIN + R или щелкните кнопку «Пуск» и выберите в главном меню команду «Выполнить». Затем напечатайте в поле ввода calc и нажмите на клавиатуре Enter либо щелкните кнопку «OK». Это же можно сделать через главное меню — раскройте его, перейдите в раздел «Все программы» и в секции «Стандартные» и выберите строку «Калькулятор». Введите последовательно все числа множества, нажимая на клавиатуре после каждого из них (кроме последнего) клавишу «Плюс» или щелкая соответствующую кнопку в интерфейсе калькулятора. Вводить числа тоже можно как с клавиатуры, так и щелкая соответствующие кнопки интерфейса. Нажмите клавишу с косой чертой (слэш) или щелкните этот значок в интерфейсе калькулятора после ввода последнего значения множества и напечатайте количество чисел в последовательности. Затем нажмите знак равенства, и калькулятор рассчитает и покажет среднее арифметическое значение.

Можно для этой же цели использовать табличный редактор Microsoft Excel. В этом случае запустите редактор и введите в соседние ячейки все значения последовательности чисел. Если после ввода каждого числа вы будете нажимать Enter или клавишу со стрелкой вниз или вправо, то редактор сам будет перемещать фокус ввода в соседнюю ячейку.

Выделите все введенные значения и в левом нижнем углу окна редактора (в строке состояния) увидите среднеарифметическое значение для выделенных ячеек.

Щелкните следующую за последним введенным числом ячейку, если вам не достаточно только увидеть среднее арифметическое значение. Раскройте выпадающий список с изображением греческой буквы сигма (Σ) в группе команд «Редактирование» на вкладке «Главная». Выберите в нем строку «Среднее» и редактор вставит нужную формулу для вычисления среднеарифметического значения в выделенную ячейку. Нажмите клавишу Enter, и значение будет рассчитано.

Вычислить среднюю скорость нетрудно. Для этого необходимо просто разделить длину пройденного пути на время. Однако на практике и при решении задач иногда возникают дополнительные вопросы. Например, что считать пройденным путем? Показания спидометра или реальное смещение объекта? Что считать временем в пути, если объект половину времени никуда не двигался? Без учета всех этих нюансов невозможно правильно вычислить среднюю скорость.

Вам понадобится

• калькулятор или компьютер, спидометр

Инструкция

Для вычисления средней скорости равномерного движения объекта, просто измерьте его скорость в любой точке пути. Так как скорость движения постоянна, то она и будет средней скоростью.
Еще проще эта зависимость выглядит в виде формулы:Vср=V, где
Vср – средняя скорость, а
V – скорость равномерного движения.

Чтобы вычислить среднюю скорость равноускоренного движения, найдите среднее арифметическое начальной и конечной скорости. Для этого найдите сумму этих скоростей и разделите на два. Полученное число и будет средней скоростью объекта.
Нагляднее это выглядит в виде следующей формулы:Vср = (Vкон + Vнач) / 2, где
Vср – средняя скорость,
Vкон – конечная скорость,
Vнач – начальная скорость.

Если задана величина ускорения и начальная скорость, а конечная скорость неизвестна, то преобразуйте вышеприведенную формулу следующим образом:
Так как при равноускоренном движении Vкон = Vнач + a*t, где а – ускорение объекта, а t – время, то имеем:Vср = (Vкон + Vнач) / 2 = (Vнач + a*t + Vнач) / 2 = Vнач + a*t / 2

Если же, наоборот, известны конечная скорость и ускорение тела, но начальная скорость не задана, то преобразуйте формулу к следующему виду:Vср = (Vкон + Vнач) / 2 = (Vкон + Vкон — a*t) / 2 = Vкон — a*t / 2

Если заданы длина пройденного телом пути, а также время, которое понадобилось на прохождение этого расстояния, то просто разделите этот путь на затраченное время. То есть используйте общую формулу:Vср = S / t, где S – общая длина пройденного пути.Время, затраченное на прохождение пути учитывается независимо от того, двигался объект непрерывно или останавливался. Если в условиях задачи специально не указано, какую именно среднюю скорость необходимо вычислить, то подразумевается средняя путевая скорость.
Чтобы вычислить среднюю путевую скорость, берется общая длина пройденного пути, т.е. его траектория. Если во время движения объект возвращался в пройденные точки пути, то это расстояние также учитывается. Так, например, для автомобиля длина пути, необходимая для вычисления средней путевой скорости, будет соответствовать показаниям спидометра (разности показаний).

Если необходимо вычислить среднюю скорость перемещения (смещения), то под пройденным путем подразумевается то расстояние, на которое тело действительно переместилось.
Так как перемещение всегда происходит в определенном направлении, то смещение (S) величина векторная, т.е. характеризуется как направлением, так и абсолютной величиной. Следовательно, и значение средней скорости смещения будет величиной векторной. В связи с этим, при решении подобных задач обязательно узнайте: какую именно скорость требуется вычислить. Среднюю путевую скорость, числовое значение средней скорости смещения или вектор средней скорости смещения.
В частности, если тело в процессе движения возвращается в исходную точку, то считается, что его средняя скорость смещения равна нулю.

С точки зрения математики средним числом может быть среднее степенное, квадратичное, гармоническое, взвешенное, логарифмическое и т.д. Однако на практике среднестатистическому человеку чаще всего приходится вычислять простую среднюю арифметическую величину какого-то набора значений. В общем виде такое среднее число можно определить как число, заключенное между наибольшим и наименьшим числами заданной последовательности.

Инструкция

Складывайте все числа исходной последовательности, а затем делите их на общее количество чисел, чтобы получить среднее арифметическое значение. Если задача носит прикладной характер, то полученный результат, возможно, следует округлять, чтобы не получить ответ в виде «полутора землекопа».

Если такое вычисление носит разовый характер, а чисел в исходной последовательности не много, то для практического расчета среднего значения можно воспользоваться калькулятором, встроенным в поисковую систему Google или Nigma. Сформулируйте и введите необходимое математическое действие в поле поискового запроса этой системы. Например, если надо найти среднее число голов, пропущенных командой ЦСКА в последних пяти играх, то введите такой запрос: «(0+1+2+1+1)/5». Результат поисковая система покажет без нажатия вами кнопки отправки запроса.

Если последовательность чисел не так мала, то лучше воспользоваться табличным редактором — например, Microsoft Office Excel. Запустив редактор, вы сразу получите в свое распоряжение таблицу для заполнения значениями исходной последовательности чисел. Сделать это можно вводя числа вручную, но если есть возможность скопировать и вставить числовую последовательность в текстовом формате, то это будет намного удобнее. В этом случае желательно с помощью любого текстового редактора перед копированием заменить все разделители между значениями последовательности на знаки перевода строки — тогда после вставки в Excel значения выстроятся в колонку. Если вместо окончания строки использовать знак табуляции, то они выстроятся в строку.

Выделите колонку (или строку), содержащую введенные значения, щелкнув ее заголовок. Среднее арифметическое значение можно будет увидеть ниже таблицы — в строке состояния.

Если только узнать это значение не достаточно, то используйте формулу для вычисления среднего. Для этого щелкните ячейку, в которой хотите увидеть результат, и раскройте выпадающий список на кнопке с пиктограммой греческой буквы сигма Σ в секции «Редактирование». Выберите в списке пункт «Среднее», а затем выделите заполненный диапазон ячеек таблицы и нажмите клавишу Enter. Excel рассчитает и отобразит среднее значение.

Источники:

• как рассчитать в excel

Среднее значение разных явлений интересует математиков, специалистов по статистике, бизнесменов и даже — спортивных обозревателей. В частности, на футбольных сайтах размещают информацию о среднем возрасте игроков в каждой команде. Такие данные получают вычислением среднего арифметического.

Инструкция

Определите начальные данные задачи. Пусть пять школьников съели на перемене по несколько конфет. Надо выяснить, сколько в среднем сладостей съел каждый ребенок. У первого было пять конфет, у второго — три, у третьего — восемь, у четвертого — семь, у пятого — две.

Найдите сумму всех чисел. В рассматриваемом примере надо вычислить, сколько конфет было съедено всеми школьниками. Сумма = 5 + 3 + 8 + 7 + 2 = 25 конфет.

Разделите результат второго шага на количество слагаемых. Среднее арифметическое = 25 / 5 = 5 конфет.

Для закрепления материала решите еще одну задачу. В понедельник в магазин канцелярских товаров зашли 112 человек, во вторник — 123 человека, в среду — 98, в четверг — 150, в пятницу — 114, в субботу — 187, в воскресенье — 210. Надо найти среднюю посещаемость магазина в течение дня.

Как и во втором шаге, просуммируйте все числа. Сумма = 112 + 123 + 98 + 150 + 114 + 187 + 210 = 994 человека. Столько посетителей было в магазине в течение одной недели.

Разделите результат пятого шага на число слагаемых, т.е. на количество учитываемых дней. Среднее арифметическое = 994 / 7 = 142 человека. Становится ясно, что в среднем в магазин приходит 142 человека в день.

Для тренировки соберите начальные данные и вычислите среднюю температуру в вашей местности за последний месяц.

Обратите внимание

Не всегда есть смысл находить среднее арифметическое. Например, вряд ли кого-то заинтересует информация о среднем росте животных. Сравните рост жирафа и мыши — между ними слишком большая разница. Поэтому вычисление среднего арифметического не имеет смысла. Думайте о практической пользе, прежде чем решать какую-либо задачу.

Полезный совет

На практике чаще будет встречаться среднее арифметическое в виде дробного числа. На шестом шаге могло получиться значение 142,8 человека в день и т.д. В таком случае может быть уместно приблизительное значение. Решение задачи будет звучать так: в среднем в магазин приходит примерно 143 человека в день.

Усреднение позволяет находить общие тенденции, понимать возможные затраты, исходя из предыдущего опыта расходов или рассчитывать бюджет на поездку. Нахождение среднего арифметического значения необходимо в науке, бизнесе и быту. Как же вычислить искомую величину?

Инструкция

Для нахождения среднего арифметического значения нужно сложить все компоненты и полученную сумму разделить на количество компонент суммы. Данную операцию можно представить формулой: среднее значение = (a(1) + a(2) + … + a(n-1) + a(n)) / n, где n — номер последнего члена суммы по порядку (количество слагаемых).

Для нахождения среднего значения члена арифметической прогрессии необходимо сложить первый член последовательности с последним и разделить полученную сумму пополам. Запись выражения математическими символами: среднее значения прогрессии = (a(1) + a(n)) / 2.

Формулы для арифметической прогрессии были разработаны великим немецким математиком Гауссом. Он же в детстве нашел способ вычисления суммы всей прогрессии с шагом 1 (ряда натуральных чисел) без отдельного сложения ее членов. Для этого юный Карл сложил первый член прогрессии с последним и умножил сумму на половинное число членов последовательности. Задача нахождения среднего арифметического значения часто встречается в программировании. Для ее простого решения нужно воспользоваться шаговым циклом (с ходом в единицу, называемым инкрементом). В большинстве языков программирования (С#, Java, Pascal, PHP) этот цикл имеет название for.

До входа в цикл объявите переменные S (сумма) и sred (среднее арифметическое). Присвойте им нулевое значение (этот процесс называется инициализацией). Входите в цикл. К сумме S прибавьте все новые члены последовательности. Так формируется полная арифметическая сумма.

После цикла выполните действие: sred = S / n. Заметьте, тип переменной S должен быть целочисленным (при целочисленных слагаемых), а sred — вещественным, так как в результате деления может получиться дробное число. Так вы получите среднее арифметическое значение в программировании.

Видео по теме

Источники:

• как находить среднее арифметическое

www.kakprosto.ru

Среднее арифметическое, размах, мода и медиана числового ряда

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Для ряда a₁,a₁,..,a_n среднее арифметическое вычисляется по формуле:

\begin{align} & \overline{a}=\frac{a_1+a_2+…+a_n}{n}\\ \end{align}

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

\begin{align} & \overline{a}=\frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\\ \end{align}

---

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

---

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

---

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

calcs.su

Вычисление среднего значения ряда чисел

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

Допустим, вам нужно найти среднее количество дней для выполнения задач разными сотрудниками. Кроме того, вы хотите вычислить среднюю температуру на определенный день в течение 10-годичного периода времени. Вычисление среднего значения для группы чисел можно выполнить несколькими способами.

Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения:

• Среднее значение    Это среднее арифметическое, которое вычисляется путем добавления группы чисел и деления их на количество этих чисел. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.

• Медиана     Средний номер группы чисел. Половина чисел содержит значения, превышающие медиану, а половина чисел содержат значения меньше медианы. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.

• Мода    Наиболее часто встречающееся число в группе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. В отклоненном распределении группы чисел они могут быть разными.

Выполните указанные ниже действия.

1. Щелкните ячейку ниже или справа от чисел, для которых нужно найти среднее значение.

2. На вкладке Главная в группе Редактирование

   щелкните стрелку рядом с кнопкой Автосумма , выберите пункт Среднееи нажмите клавишу ВВОД.

Для выполнения этой задачи используется функция СРЗНАЧ . Скопируйте таблицу, расположенную ниже, на пустой лист.

Формула	Описание (результат)
= СРЗНАЧ (A2: A7)	Вычисляет среднее значение всех чисел в приведенном выше списке (9,5)
= СРЗНАЧ (A2: A4; A7)	Вычисление среднего значения первых трех значений и последнего числа в списке (7,5)
= СРЗНАЧЕСЛИ (a2: A7; «<>0»)	Усредняет числа в списке за исключением тех, которые содержат ноль, например ячейку A6 (11,4).

Для выполнения этой задачи используйте функции СУММПРОИЗВ и Sum . в ВСИС примере рассчитываются средние цены, оплаченные за единицу в трех покупках, где каждая из них предназначена для разных единиц товара на разных единицах.

Скопируйте таблицу, расположенную ниже, на пустой лист.

A B Цена за единицу Количество единиц 20 500 24 750 35 200 Формула Описание (результат) = СУММПРОИЗВ (A2: A4; B2: B4)/СУМ (B2: B4) Делит общие затраты на все три заказа на общее количество заказанных единиц (24,66).

Для выполнения этой задачи используйте функции

СРЗНАЧ и Если . Скопируйте приведенную ниже таблицу и имейте в виду, что этот пример проще понять при копировании на пустой лист.

Формула	Описание (результат)
= СРЗНАЧЕСЛИ (a2: A7; «<>0»)	Усредняет числа в списке за исключением тех, которые содержат ноль, например ячейку A6 (11,4).

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

См. также

СРЗНАЧ

СРЗНАЧЕСЛИ

СУММ

СУММПРОИЗВ

support.office.com