Разложить элементарную функцию f x на заданном интервале в ряд фурье – .

Содержание

4.7. Разложение в ряд Фурье непериодических функций, заданных на конечном промежутке

Пусть непериодическая функция f(x) задана на некотором отрезке [a,b] и пусть она на этом отрезке непрерывна или имеет конечное число точек разрыва первого рода, и отрезок [a,b] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна. Покажем, что данную функцию в точках непрерывности можно представить в виде суммы ряда Фурье.

Рассмотрим функцию f*(x) с периодом Т = 2l≥b-а, удовлетворяющую условиям Дирихле на отрезке [—l,l] и совпадающую с данной функцией на отрезке [a,b] (рисунок 8).

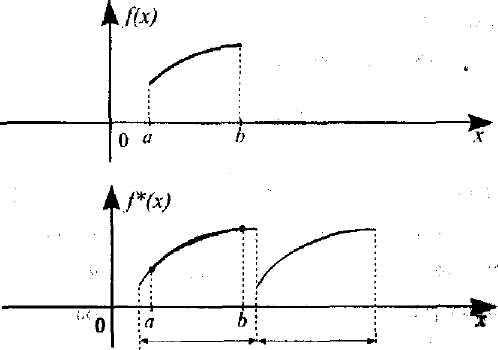
Рисунок 8

Найдем разложение функции f^* (х) в ряд Фурье. Сумма этого ряда во всех точках непрерывности совпадает с функцией f^* (х). Так как на отрезке [a,b] функция f(x) совпадает с функцией f^* (х), то сумма ряда во всех точках отрезка [a,b], кроме точек разрыва, совпадает с заданной функцией, таким образом, мы разложили в ряд Фурье функцию f(x) на отрезке [a,b]

Если функция f(x) задана на отрезке [0,l] и непрерывна или кусочно-непрерывна на этом отрезке, то можно найти разложение функции в ряд косинусов или синусов. Для этого достаточно доопределить функцию на отрезке [

—l,0] так, чтобы ее значения в точках отрезка [—l,0] находились из условия f(-x) = f(x) или f(-x)=-f(x). В этом случае говорят, что функцию доопределяем четным или нечетным образом. При этом коэффициенты ряда Фурье находятся по упрощенным формулам для четных или нечетных функций.

Пример 33

Разложить в ряд Фурье функцию напряжения на сетке лампы: .

Решение.

Построим график данной функции на отрезке [0,π]. Рассмотрим, вспомогательную функцию, которая на отрезке [0,π] совпадает с данной. Для этого, продолжив заданную функцию четным образом на отрезке [-π,0], будем рассматривать периодическую функцию U^* (ωt)

с периодом Т = 2π (рисунок 9),

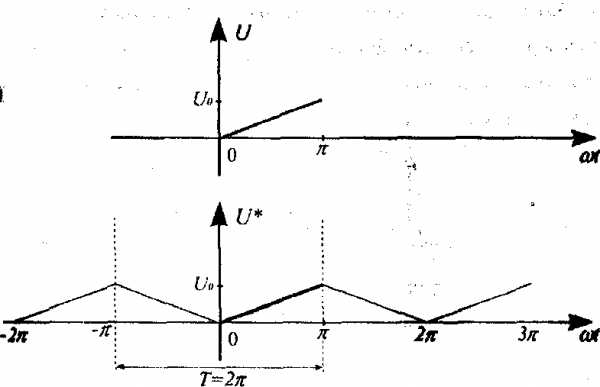
Рисунок 9

Функция U^* (ωt) является четной, значит, b_п=0. Полагая ωt=х, найдем a_O, а_n:

Заметим, что при интегрировании использовали формулу интегрирования по частям:

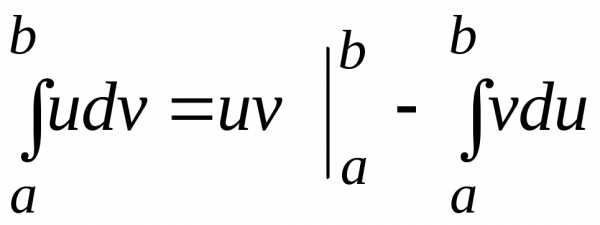
Возвращаясь к исходной переменной 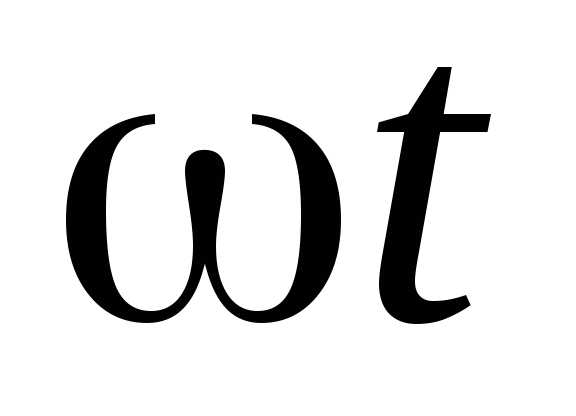, запишем ряд Фурье

Полученный ряд сходится на всей числовой оси к функции U^* (ωt), так как функция непрерывна на всей числовой оси. А поскольку данная функция U(ωt) совпадает с U^* (ωt) при ωt [0, π], то справедливо разложение

Замечание. В индивидуальном задании требуется найти разложение в ряд Фурье функции, заданной графически. Чтобы вычислить коэффициенты Фурье, нужно перейти от графического способа задания функции к аналитическому.

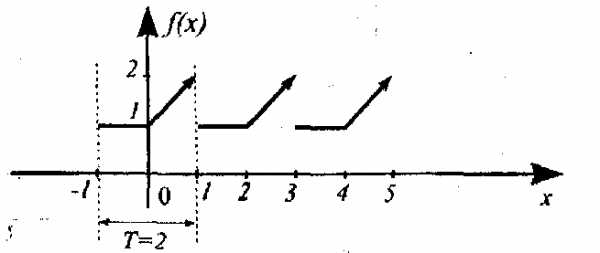
Рисунок 10

Например, если функция f(x) задана графически (рисунок 10), то на отрезке [-1,1] график состоит из части горизонтальной прямой

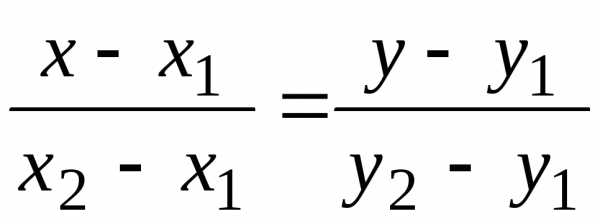у =1 при х[-1,0) и части наклонной прямой, проходящей через точки (0,1) и (1,2). Из аналитической геометрии известно, что если прямая проходит через точки (х₁, у₁) и (х₂, у₂), то ее уравнение имеет вид

Уравнение наклонной прямой, проходящей через точки (0,1) и (1,2):

Итак, на отрезке [-1,1] аналитическое задание функции

Заметим, что данная функция f(x) является периодической с периодом Т=2, т.е. функция удовлетворяет условию f(x + 2)= f(x).

studfiles.net

3.4. Ряд Фурье для четных и нечетных функций

В некоторых случаях формулы (4) для вычисления коэффициентов Фурье могут быть упрощены. Это имеет место для четных и нечетных функций. Следует учесть, что если f(x) – четная на промежутке [-a, a], то

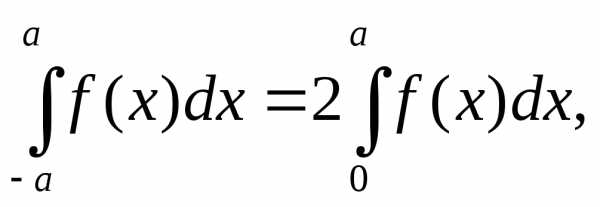
если же f(x) – нечетная, то

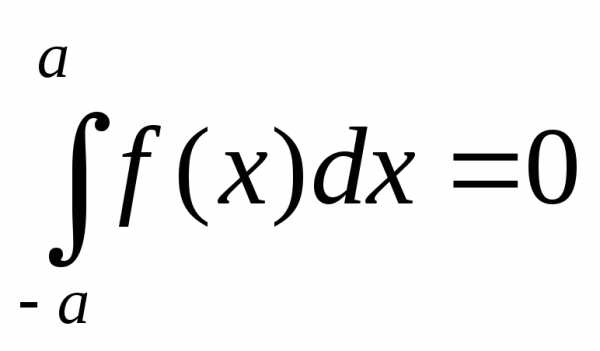Допустим теперь, что нужно разложить в ряд Фурье четную функцию f

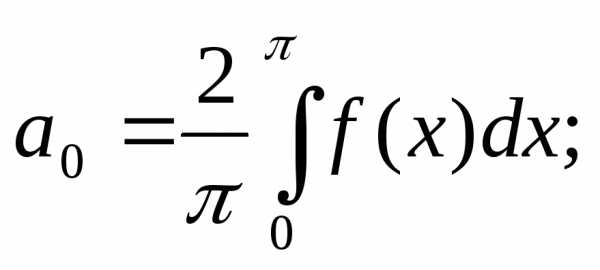
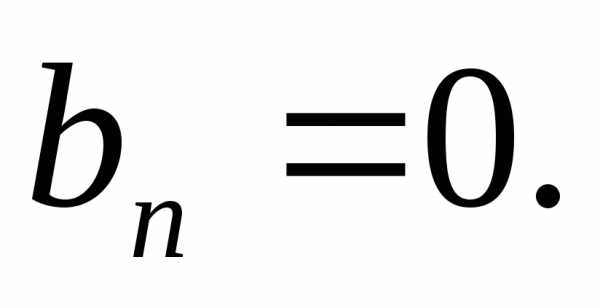(x). На основании свойств четных и нечетных функций, а также формул (4), получили

(5)

Соответственно этому ряд Фурье для четной функции имеет вид:

. (6)

По аналогии для нечетной функции f(x) получим:

. (7)

Ряд Фурье для нечетной функции имеет вид:

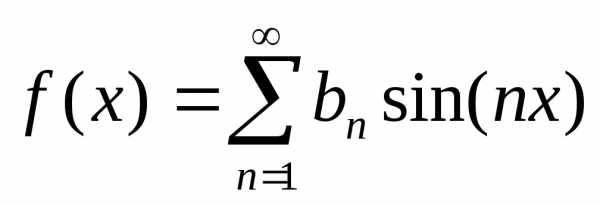. (8)

Таким образом, четная функция раскладывается в ряд только по косинусам, а нечетная функция – только по синусам кратных дуг.

Разложение в ряд Фурье функции с периодом 2l

Часто приходится раскладывать в тригонометрический ряд функции, период которых отличен от . Этот случай легко сводится к изученному ранее с помощью замены переменной.

Для функции f(x), имеющей период 2l, коэффициенты Фурье вычисляются по формулам:

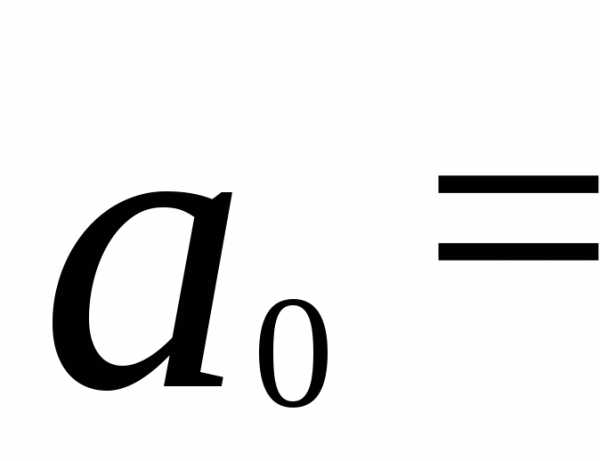
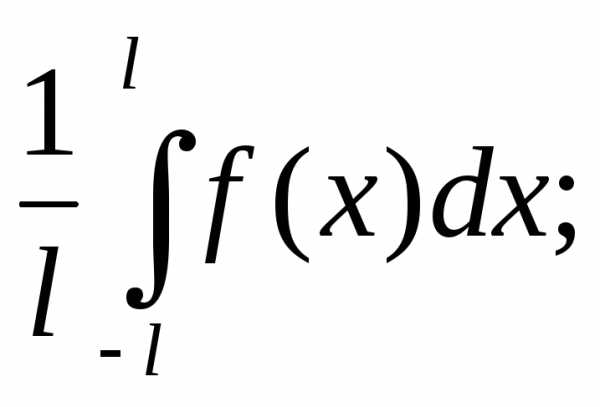(9)

Ряд для функции f(x) имеет вид:

(10)

Пример 1.

Разложить в ряд Фурье функцию периода 2l

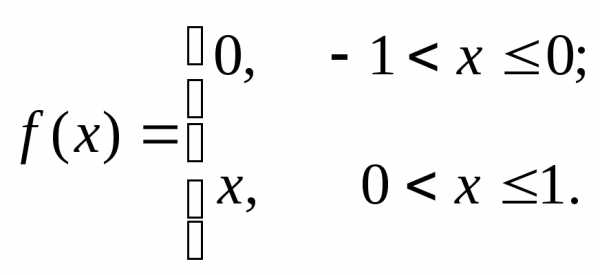
=2, заданную на отрезке [-1;1] равенством

Решение. Найдем коэффициенты Фурье, используя формулы (9).

По формуле (10) записываем искомый рад Фурье:

Формулы (9) и (10) для коэффициентов Фурье и ряда Фурье четных и нечетных функций с периодом 2l преобразуются следующим образом.

Для четной функции:

, ,,

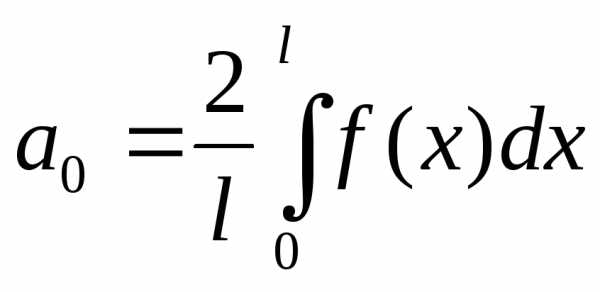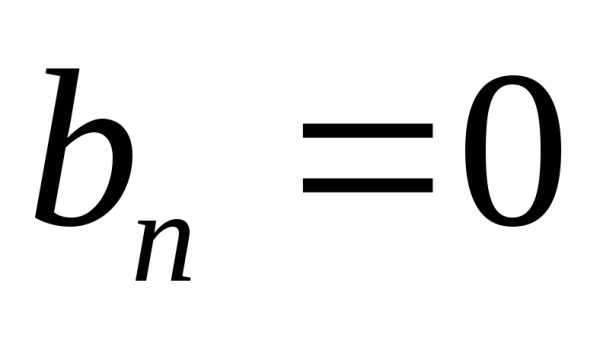. (11)

Для нечетной функции:

, ,

. (12)

Разложение в ряд Фурье непериодических функций

Пусть f(x) – непериодическая функция, заданная на всей числовой оси. Если необходимо разложить её в ряд Фурье на промежутке [-l;l], то вводят вспомогательную функцию с периодом2l, значения которой совпадают со значениями f(x) на промежутке [0;l]. Если функция 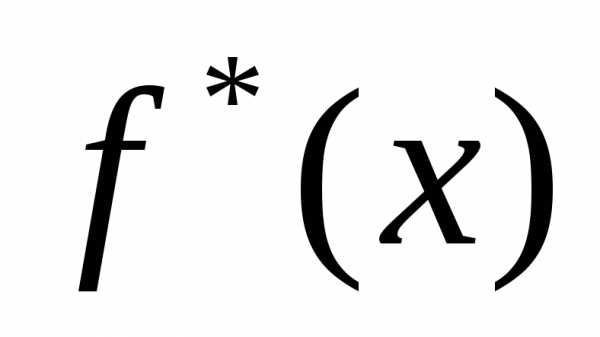удовлетворяет условиям Дирихле, то её можно представить соответствующим рядом Фурье.

Иногда приходится иметь дело с функциями, заданными только на промежутке [0;l]. В этом случае мы можем сначала продолжить функцию на интервал (-l;0), а затем продолжить её на всю числовую ось периодически с периодом 2l

. Чаще всего функцию продолжают четным или нечетным образом. Таким образом можно получить бесчисленное множество рядов Фурье для функции f(x), заданной на промежутке [0;l].

Пример 1.

Разложить в ряд по синусам функцию f(x)=1, заданную на промежутке (0;l].

Решение. Для разложения функции в ряд по синусам надо сначала её продолжить на промежуток [-1;0] нечетным образом, а затем полученную функцию продолжить периодически на всю числовую ось. Тогда график функции будет иметь вид:

Коэффициенты ряда вычисляются по формулам (12). Здесь надо принять l=1, f(x)=1. Тогда:

Итак:

, ,,,,, …

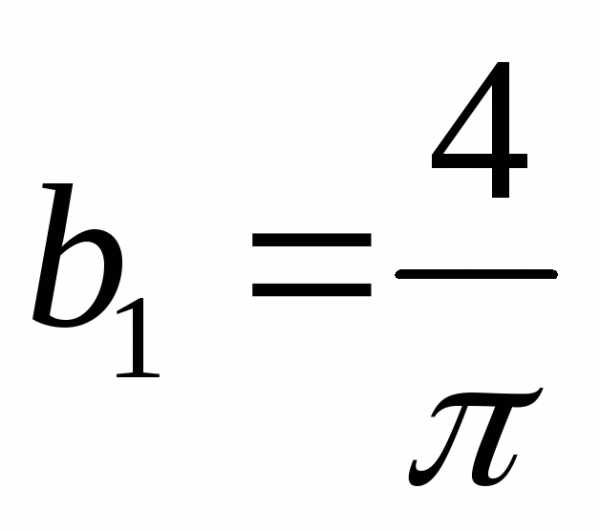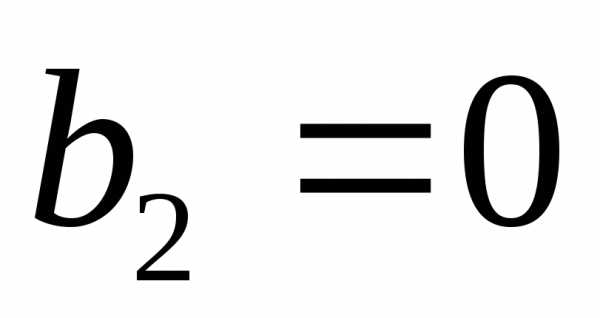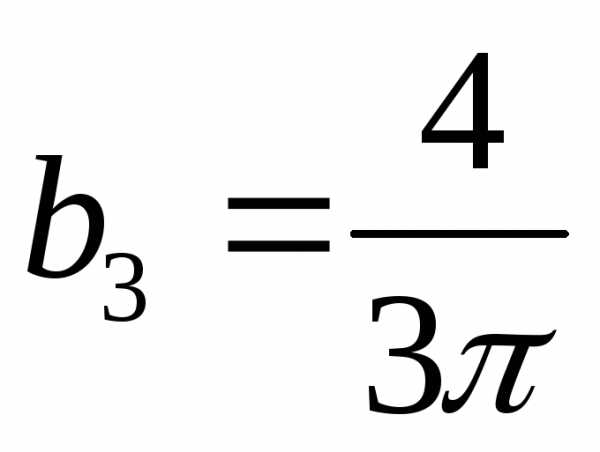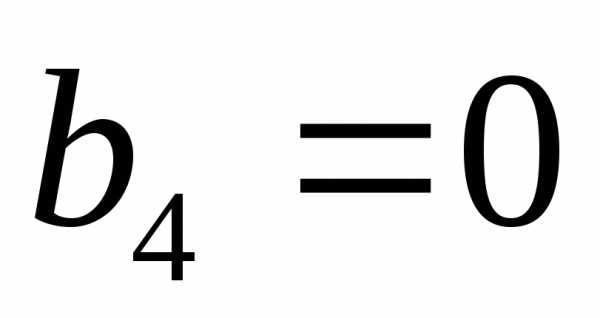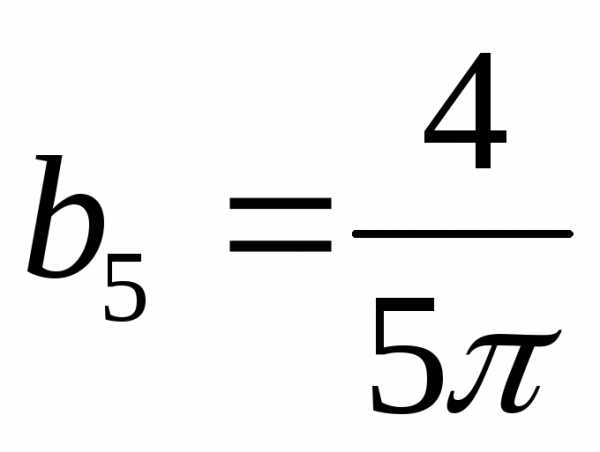Ряд Фурье для данной функции имеет вид:

studfiles.net

Разложить в ряд Фурье функцию f (x), заданную на интервале (0; π), продолжив (доопределив) ее чётным и нечетным образом. Построить графики для каждого продолжения.

Разложить в ряд Фурье функцию f (x), заданную на интервале (0; π), продолжив (доопределив) ее чётным и нечетным образом. Построить графики для каждого продолжения.

1.	f ( x ) = e ^x	2.	f ( x )= x²	3.	f ( x )= x²
4.	f ( x ) = ch x	5.	f ( x ) = e^{– x}	6.	f ( x ) = (x – 1)²
7.	f( x ) = 3^{– x / 2}	8.	f ( x ) = sh 2x	9.	f ( x ) = e^{2 x}
10.	f ( x ) = ( x – 2 ) ²	11.	f (x)= 4 ^{x / 3}	12.	f ( x ) = ch x /2
13.	f ( x )= e^{4 x}	14.	f ( x ) = (x + 1)²	15.	f ( x ) = 5^{– x}
16.	f ( x ) = sh 3 x	17.	f ( x ) = e^{– x / 4}	18.	f ( x ) =( 2 x – 1) ²
19.	f ( x ) = 6 ^{x / 4}	20.	f ( x ) = ch 4 x	21.	f ( x ) = e ^{– 3 x}
22.	f ( x ) = x ² + 1	23.	f ( x ) = 7^{– x / 7}	24.	f ( x ) = sh x /5
25.	f ( x ) = e^{– 2 x / 3}	26.	f ( x ) = ( x – π ) ²	27.	f ( x ) = 10 ^{– x}
28.	f ( x ) = ch x / π	29.	f ( x ) = e^{4 x / 3}	30.	f (x) = ( x – 5 )²

Задание 6.14.

Разложить в ряд Фурье в указанном интервале периодическую функцию f (x) с периодом .

Задание 6.15.

Воспользовавшись разложением функции f(x) в ряд Фурье в указанном интервале, найти сумму данного числового ряда.

Дата добавления: 2015-08-17; просмотров: 268 | Нарушение авторских прав

Задание 6.6. | Задание 6.7. | Разложить в ряд Маклорена или в ряд Тейлора функцию f(x) в окрестности указанной точки x . Указать область сходимости полученного ряда. |

mybiblioteka.su — 2015-2019 год. (0.004 сек.)

mybiblioteka.su

4.7. Разложение в ряд Фурье непериодических функций, заданных на конечном промежутке

3.4. Ряд Фурье для четных и нечетных функций

Разложение в ряд Фурье функции с периодом 2l

Разложение в ряд Фурье непериодических функций

Разложить в ряд Фурье функцию f (x), заданную на интервале (0; π), продолжив (доопределив) ее чётным и нечетным образом. Построить графики для каждого продолжения.

Добавить комментарий Отменить ответ