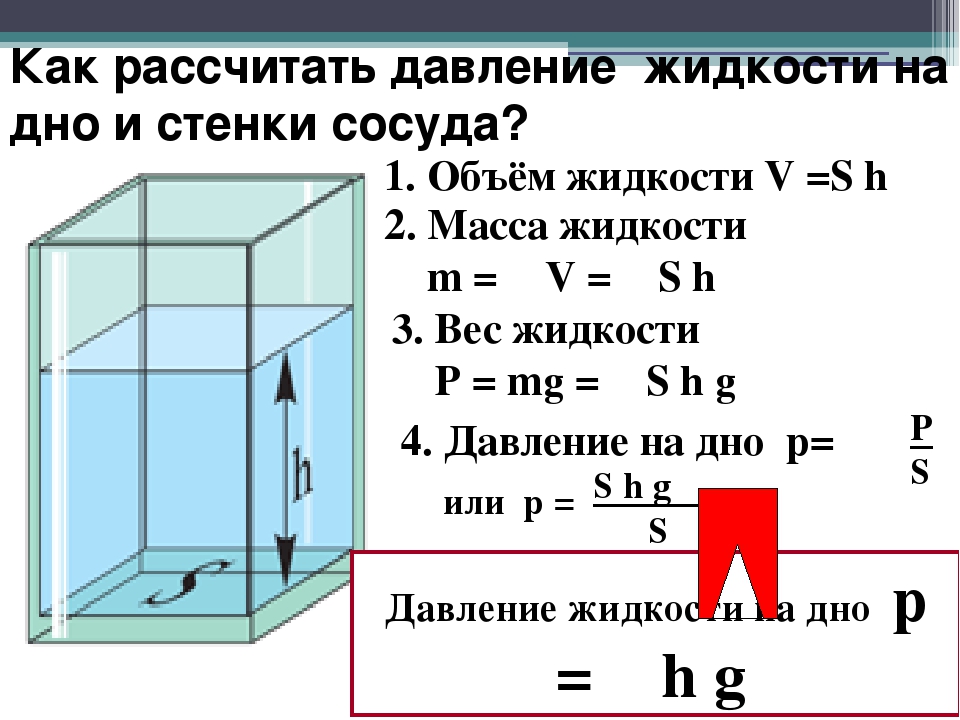
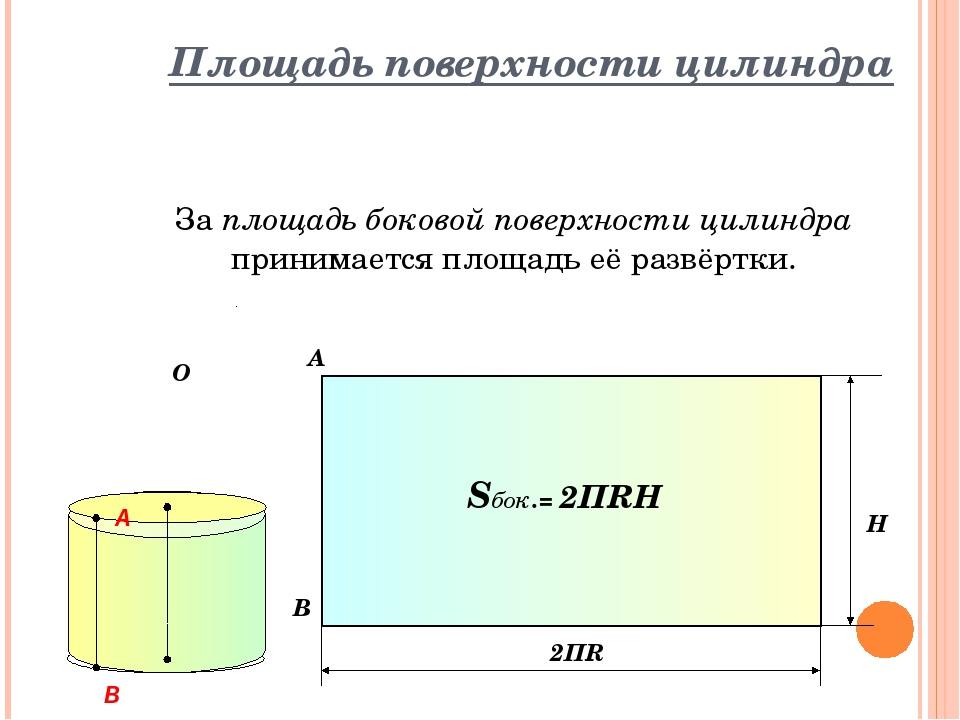
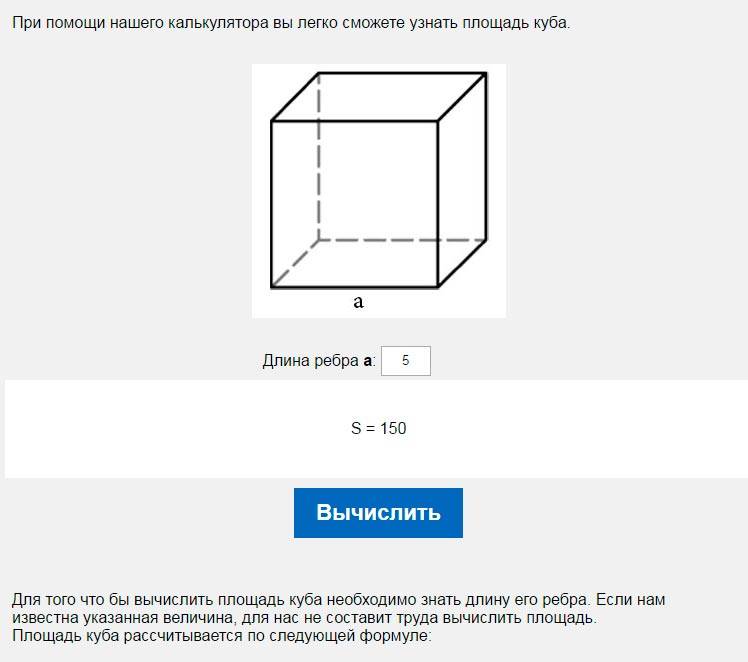
как найти площадь зная высоту и объем?
Сынып оқушыларына жүргізілген «Ең суйiктi спорт түріңіз қандай?» сауалнамасының көрсеткіші кестедекөрсетілген.а) Сыныпта қанша оқушы бар?b) Кестеде бе … рілген мәліметтерді қолданып, бағанды диаграмма тұрғызыңыз.Спорт түріОқушы ТаңдауыТеннис 3Баскетбол 8Жүзу 4Футбол 16Бокс 5
[20.05, 06:53] Сауле Бегиндиковна.: 4.Запиши краткую запись и реши задачу. На праздник для украшения купили 3пачки шаров по 43 тенге и 6 лен … т по 25 тенге. На сколько тенге больше заплатили за ленты, чем за шары?[20.05, 06:54] Сауле Бегиндиковна.: 5. Реши задачу.Площадь прямоугольника 120 см², а длина 40см. Найди ширину и периметр прямоугольника.
б) Продавец продал 13 кг, 15 кг, 14 кг, 18 кг, 11 кг, 12 кг, 10 кг, 21 кг, 12 кг груш за 9дней соответственно. Найдите размах, среднее арифметическое,
… моду и медиануполученного ряда.Решите задачи:а) Объём прямоугольного параллелепипеда равен V см2, стороны его основания равны 3см и 12 см, а высота һ см.
Сколько будет 0+3•6+40-20
4G12:03 Oвариант. Выполни задания на вычисления статистических числовых характеристиш..а) Верно ли утверждение:Напишите «Да», если утверждение верно, … «Нет» — утверждение ложно.Сегодня, 11:01Да/НетУтверждение1) Температура воздуха утром составляла 3°С, днем — 15°С, вечером8°C. Среднее арифметическое температуры за день составляет15°С.2) В классе 4 ученика имеют рост 1,4 м; 7 учеников — 1,5 м; 5 человек1,3 м. В ряду данных 1 мода -1,5 м.3) В ряду 1,3; 2,9; 5,8; 7,6; 9,5 медиана является число 5,84) В магазине осталось три арбуза весом 7,9 кг, 12,1 кг и 5,8 кг.Размах веса арбузов составляет 4,2 кг.
4. Kesmalarni belgilash uchun ularning ikki chetigaA, B, C, D harflardan biri qoʻyiladi.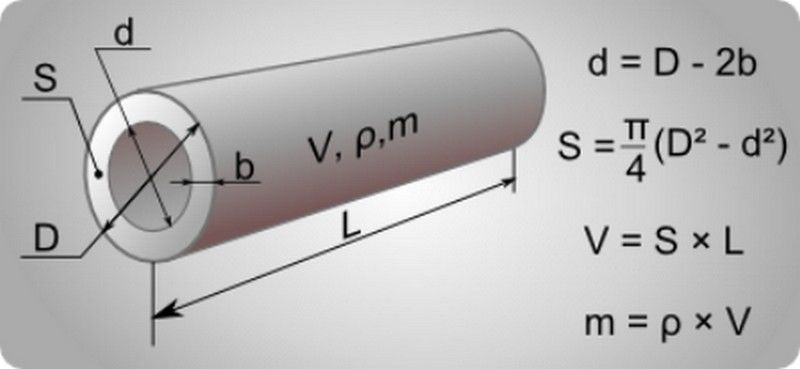 Bu harflardanfoydalanib ikkita bir xil harf qoʻyilmagan necht
… akesma yasash mumkin?hoʻlgan nredmetlarni toping:
Bu harflardanfoydalanib ikkita bir xil harf qoʻyilmagan necht
… akesma yasash mumkin?hoʻlgan nredmetlarni toping:
В таблице представлены результаты учеников принимавших участие в художественной выставке. a) Сколько учеников принимало участие в выставке? b) Построй … те столбчатую диаграмму по данным из таблицы. Число картин нарисованных карандашом 0 1 2 3 4 5 6 Количество учащихся 2 3 7 11 8 9 5
путешественники шли пешком 3 часа. Затемостановились на привал на 50 минут. Послеэтого они прошли ещё 7 часов. Сколько всеговремени путешественники бы … ли в пути?
действие 94 секунды X2 равно сколько-то минут сколько это секунд второе 950 лет разделить на 5 равно
j4266 29 : 38 2033. Ifodalarni yozing:a) Koʻylak narxi x soʻm, shim esa undan 4 martaqimmat. Shim va ko’ylak birgalikda necha soʻm?b) Qovoq massasi b
… kg, handalakniki esa undan2 kg yengil. Ularning birgalikdagi massasini toping.d) Hovuzga k litr, sisternaga esa undan 9 martakam suv sigʻadi.
Как посчитать объем цилиндра — онлайн калькулятор
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.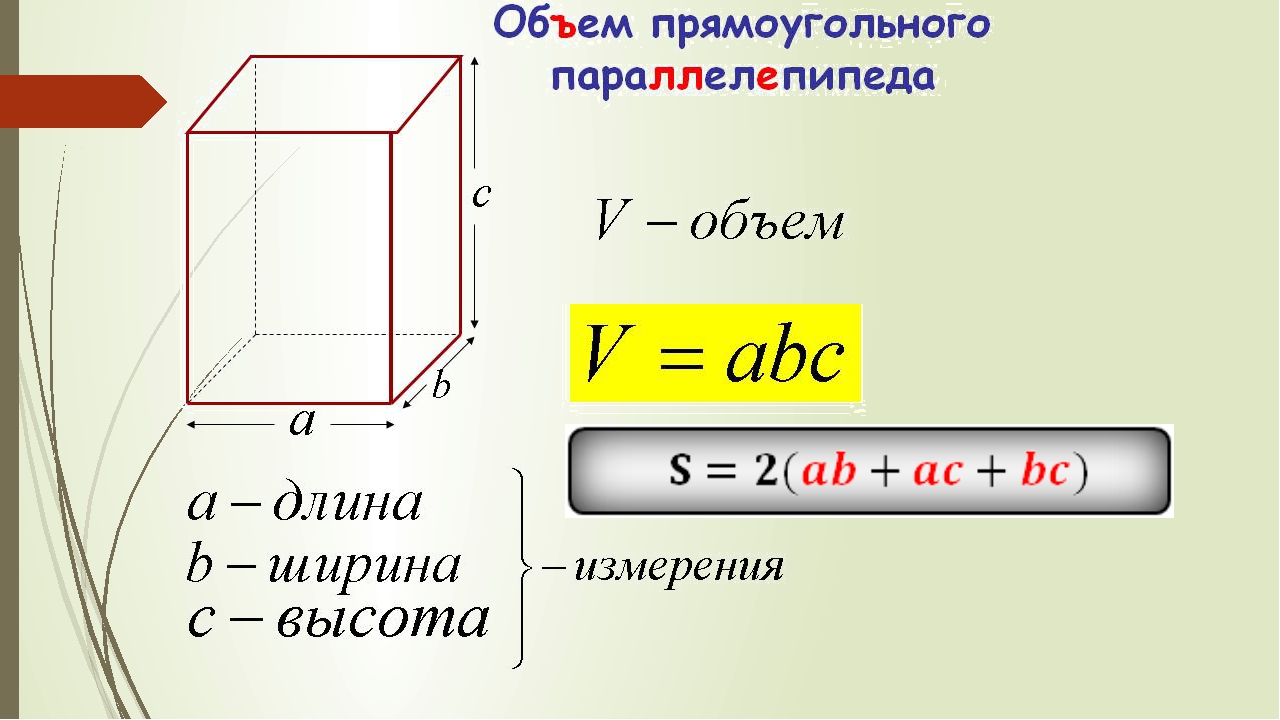 14156 ⋅ 32 = 100.53 см3
14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания S
o и высоту hЧему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
V = So⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см
Зная площадь боковой поверхности S
b и высоту hЧему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
V = Sb2/4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3. 14⋅ 5 = 900/62.8 = 14.33 см3
14⋅ 5 = 900/62.8 = 14.33 см3
См. также
Рассчитать объем щебня по площади: таблицы и формулы
В этой статье подробно описано, как рассчитать объем щебня по площади. Чтобы вычислить его, нужно перемножить насыпную плотность нерудного материала, длину и ширину участка, который предстоит засыпать, а также толщину щебневого слоя.
Важные характеристики щебня
Насыпная плотность – масса 1 куб. м щебня в неуплотненном состоянии. Она указана в сертификате соответствия и различна для разных фракций и видов материала. Например, известняк — самый легкий из-за слоистой и пористой структуры, а гранит — наиболее тяжелый ввиду высокой плотности. Если нет возможности ознакомиться с сертификатами, ориентируйтесь на примерные показатели в соответствии с ГОСТ 8267-93, ГОСТ 8269.0-97.
Таблица 1. Насыпная плотность щебня разных видов
| Щебень | Размер фракции,мм | Насыпная плотность,кг/м3 |
|---|---|---|
| Гранитный | 20 – 40 | 1370 – 1470 |
| 40 – 70 | 1380 – 1450 | |
| 70 – 250 | 1400 | |
| Известняковый | 10 – 20 | 1250 |
| 20 – 40 | 1280 | |
| 40 – 70 | 1330 | |
| Гравийный | 0 – 5 | 1600 |
| 5 – 20 | 1430 | |
| 20 – 40 | 1400 | |
| 40 – 100 | 1650 | |
| >160 | 1730 | |
| Шлаковый | независимо от размера частиц | 800 |
Перед тем как рассчитать, сколько нужно щебня на площадь, проанализируйте сопутствующие факторы. Основной из них – коэффициент уплотнения. Эта безразмерная величина характеризует, насколько объем материала уменьшится при трамбовке катком или в ходе естественного уплотнения при перевозке. ГОСТ 8267-93 не требует обязательного указания этого параметра в сопроводительных документах, поэтому ориентируйтесь на условия СНиП 3.06.03-85:
Основной из них – коэффициент уплотнения. Эта безразмерная величина характеризует, насколько объем материала уменьшится при трамбовке катком или в ходе естественного уплотнения при перевозке. ГОСТ 8267-93 не требует обязательного указания этого параметра в сопроводительных документах, поэтому ориентируйтесь на условия СНиП 3.06.03-85:
- при транспортировке в грузовой машине коэффициент равен 1,1;
- при трамбовке высокопрочных марок гранитной, гравийной щебенки– около 1,3;
Показатель актуален для насыпных материалов с размером фракций 40 – 70 и 70 – 120 мм. Для других видов его обычно не применяют, поскольку в дорожно-строительных работах мелкую щебенку используют для расклинцовки (заполнения пустот), а не для обустройства оснований. Однако из нее делают фундаментную подушку, а для этих целей подходит щебенка 20 – 40 мм. Если нужно произвести расчет щебня для фундамента, также применяйте коэффициент 1,3.
Пример расчета для фундамента
Рассчитать щебень на фундамент предельно просто. В первую очередь вычисляют объем щебневой подушки по формуле:
V= Sh= abh, где:
S – площадь, а h – высота,
a – длина, b – ширина, h – высота.
Поскольку мы рассчитываем объем щебня по площади, она нам уже известна. Ее следует умножить на толщину подушки (рекомендованное значение – от 20 до 30 см). Если размеры монолитного фундамента равны 6х10 м, а толщина щебеночного слоя – 25 см, рассчитаем объем:
6 х 10 х 0,25 = 15 куб. м
Для фундаментной подушки традиционно используют нерудные материалы с показателями морозостойкости не менее F300, прочные и стойкие к воздействию влаги. Обычно это гранит или гравий. Но первый существенно дороже, а также обладает природной радиоактивностью, поэтому строить жилые дома с его применением следует очень осторожно (например, нельзя использовать его при возведении стен, перекрытий).
Насыпная плотность гравийного щебня 20 – 40 мм – около 1400 кг/куб. м, а коэффициент уплотнения в данном случае – 1,3. Зная эти параметры, произведем несложный расчет:
1,4 т х 15 куб. м х 1,3 = 27,3 т.
Мы получили общий вес нерудных материалов для засыпки 60 кв. м площади слоем в 25 см. Чтобы рассчитать необходимый объем, делим полученную величину на насыпную плотность материала:
27,3 т : 1,4 т/куб. м. = 19,5 куб. м
Расчет щебня на дорогу
Пользуясь приведенными формулами, несложно понять, как рассчитать количество щебня на дорогу. Просто подставьте необходимые значения:
V = S пл.покрытия х h толщина слоя
Полученный объем перемножьте с насыпной плотностью щебенки (обычно используют гранитную 70 – 120 мм) и коэффициентом 1,3 по формуле:
m = V х уд. плотность х коэфф. уплотнения
Затем разделите массу на удельную плотность и получите объем щебня, который нужно приобрести для проведения строительных работ.
Доставка нерудных материалов по ЦФО
Позвоните нам!
или оставьте заявку
Как посчитать длину стен, зная площадь комнаты
Статья будет полезна тем, кто столкнулся с необходимостью рассчитать планировку комнат в новостройке. Имеющийся на руках план всегда содержит информацию о площадях помещений квартиры, но не всегда в нем есть информация о длинах стен, перегородок, дверных и оконных проемов и т.д. Мы расскажем о том, как восполнить этот недостаток, воспользовавшись незатейливыми математическими расчетами, которые будут понятны даже семикласснику.
Предположим, у нас есть план квартиры, такой как показан на рисунке ниже. Этот план нам потребуется в электронном виде – в виде картинки, которую мы сможем открыть графическим редактором (например, в формате .jpeg или .png).
Если у Вас план только на бумаге, то можно его ровно без перекосов сфотографировать и сохранить в компьютер или загрузить с сайта застройщика, если такая возможность имеется.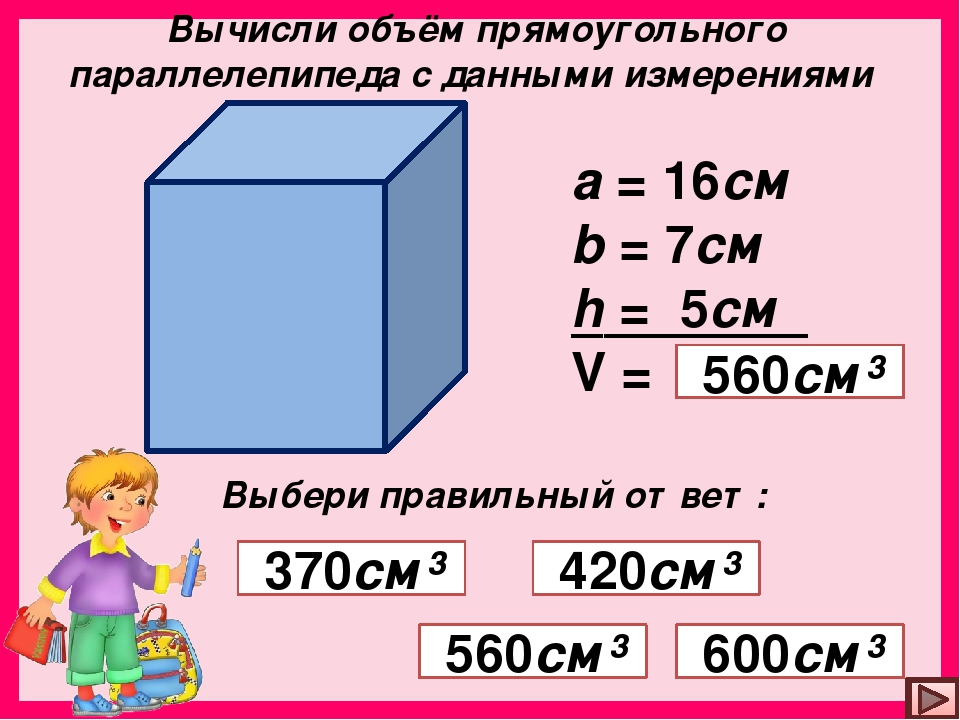
В нем нам нужно выбрать любую комнату строго прямоугольной формы (или квадратной). В нашем примере выберем кухню, площадь которой нам известна, и составляет 15,13 квадратных метров.
Условно обозначим длину одной стороны прямоугольника буквой «a», длину другой «b», как принято в школьном курсе геометрии.
Площадь прямоугольника, как мы помним определяется произведением его сторон:
С помощью встроенного графического редактора Paint или другого, например, PickPick открываем наше изображение с планом квартиры. Затем с помощью инструмента «Выделение» вычисляем длину и ширину нашего прямоугольника в пикселях, как показано на рисунке ниже.
Полученные значения запишем, обозначив их, например, как «a» со штрихом и «b» со штрихом, для длины и ширины комнаты соответственно.
Более точной единицей измерения для полученных значений будет не «пиксель», а скорее сторона пикселя, поскольку пиксель представляет собой квадрат определенной площади и для измерения длин не очень подходит.
Подсчитаем площадь комнаты в пикселях:
Далее, введем коэффициент, который будет показывать насколько отличается длина стороны пикселя нашего изображения от длины квадратного метра. Обозначим этот коэффициент буквой «k».
Искомые значения длины и ширины комнаты, будут найдены по формуле:
Остается выяснить чему равен коэффициент. Для этого составим простое уравнение, из которого элементарно находим значение коэффициента, как корень из соотношения площадей в пикселях и в квадратных метрах.
Подставляем значение найденного коэффициента в формулы для нахождения длины и ширины комнаты и получаем искомые величины.
Зная коэффициент, мы можем получить длину в метрах для любого объекта в имеющемся плане. Нужно только узнать длину этого объекта в пикселях и умножить полученное значение на коэффициент.
Обращаю внимание, что значение вычисленного коэффициента подходит только для данного конкретного изображения, из которого этот коэффициент вычислялся. Если возьмете другое изображение, то коэффициент придется считать заново.
Если возьмете другое изображение, то коэффициент придется считать заново.
Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объемСодержание статьи
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.

- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнатыНайденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формыПокажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формыВ этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигурЕще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на планТак как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв. м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнатыДля некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
| Радиус: | ||
| Высота: | ||
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Формула объема цилиндра: , где R – радиус оснований, h – высота цилиндра | ||
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах.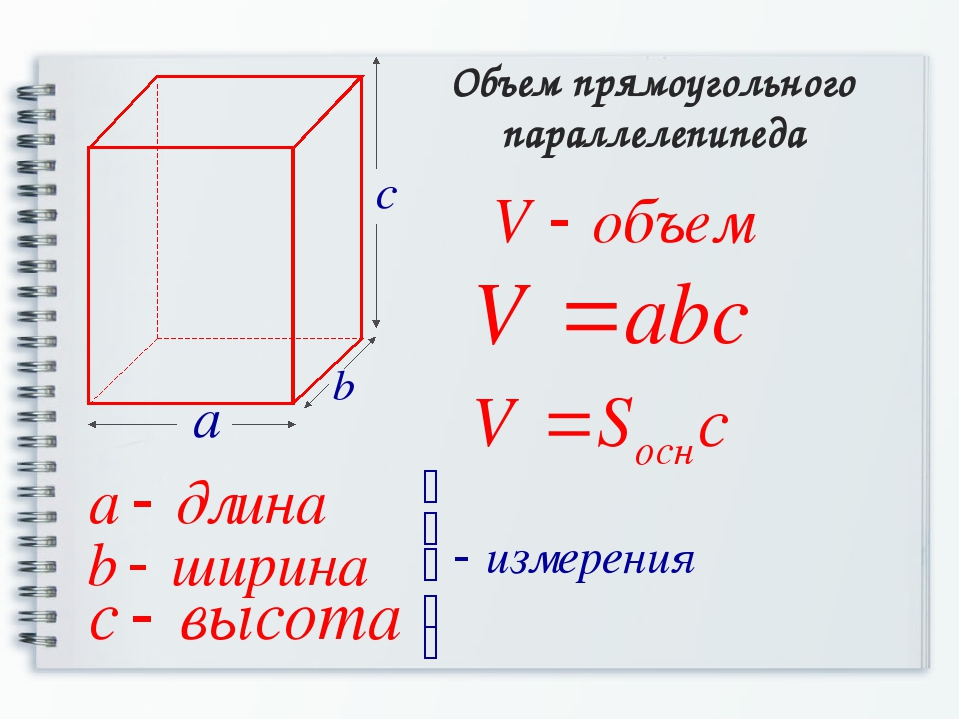 Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м3 >;
зная равенство: 1 м3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности.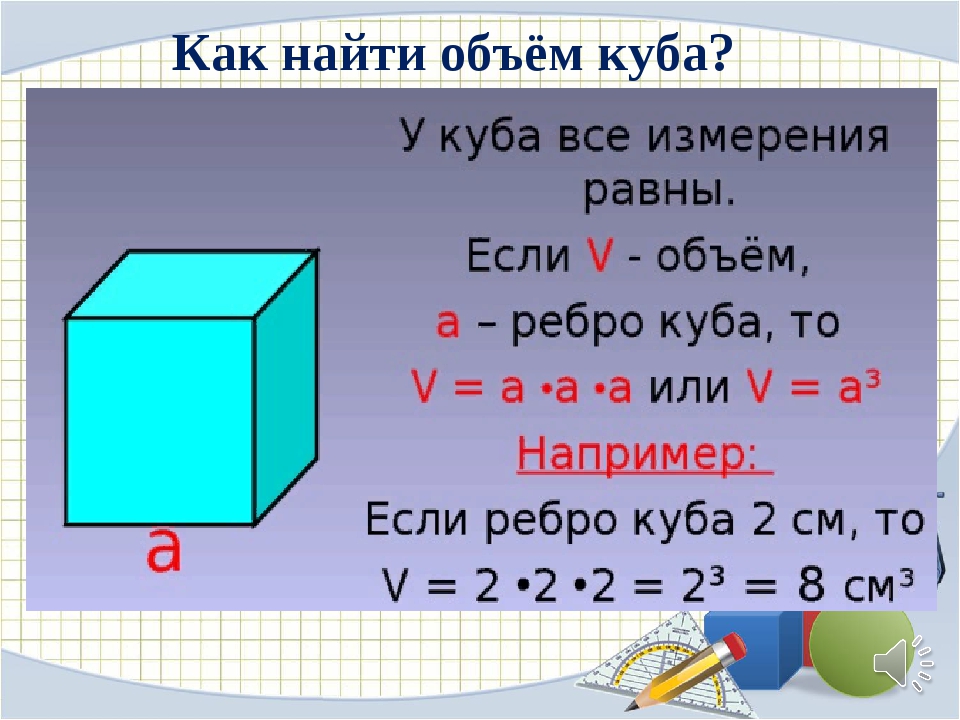 Данные отрезки называются образующими цилиндра.
Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
[ LARGE V = S cdot H ]
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.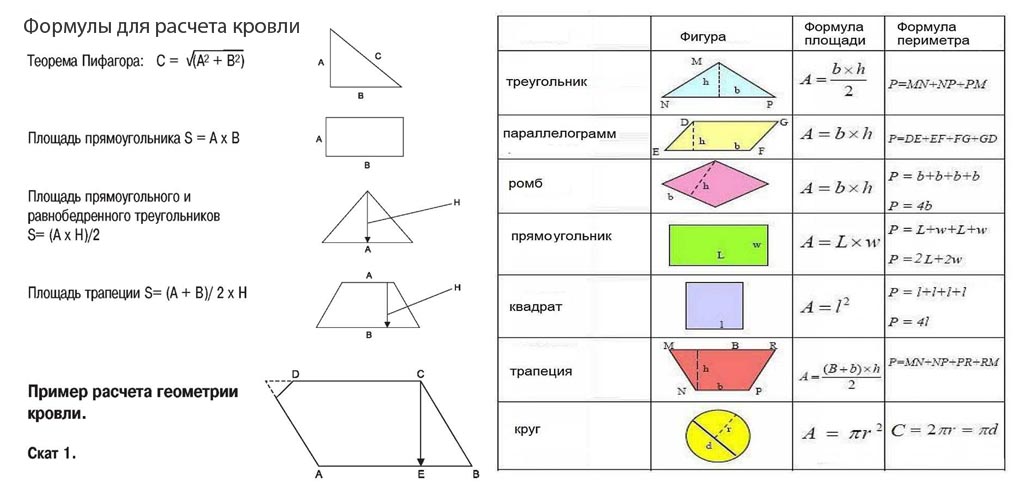
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Формула расчета объема цилиндра
Объем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр.
Найти объем цилиндра
Выберите известные величины:Введите данные:
Вводить можно числа или дроби (-2.4, 5/7, …).
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://mnogoformul.ru/obem-cilindra
- https://poschitat.online/obem-cilindra
- https://MicroExcel.ru/obyom-tsilindra/
- https://www.calc.ru/obyem-tsilindra.html
- https://gofro-karton.com/blog/rasschitat_obem_korobki/
- https://tara-tovara.
 ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/ - https://doza.pro/art/math/geometry/cylinder
- https://calcsbox.com/post/formula-obema-cilindra.html
- https://kalkulyator-nds.com/obem-cilindra-kalkulyator
- https://ru.onlinemschool.com/math/assistance/figures_volume/cylinder/
Как рассчитать объем бетона? 👷 Евробетон
При составлении строительных смет производится расчет материалов. Их стоимость и расход позволяют определить общую цену застройки, а также сэкономить на возведении несущей конструкции. Зная объем бетонной смеси для каждого типа фундаментов, владелец застройки сможет правильно подобрать основание для своего дома.
Расчет объема бетона для свайного фундамента
Столбчатый фундамент – несущая конструкция, для возведения которой используют винтовые сваи и бетонную заливку. Независимо от типа сечения, расход материалов рассчитывается по формуле:
V= S*H, где:
- V – размер лунки;
- S – площадь ее основания;
- H – высота лунки.

Площадь фундамента свайной лунки – это:
S=п*R2, где:
- п – 3.14;
- R – радиус лунки/половина диаметра.
Для свай квадратного сечения расчет аналогичен.
В случаях, когда сваи не вбиваются в землю, а устанавливаются в бетонные короба, их кубатура также учитывается.
Формула для ленточного фундамента
Ленточный фундамент – это железобетонная контурная конструкция в основании постройки. Ее параметры соответствуют расположению несущих стен, а глубина зависит от этажности и типа грунта. Для расчета простого ленточного монолита используется следующая формула:
V = S * L, где:
- V – вычисляемые габариты фундамента;
- S – площадь основания;
- L – общая длина фундаментной ленты.
Площадь (S) вычисляют путем сложения ширины ленты (a) и ее высоты (b):
S=a*b
Для увеличения несущей способности конструкции строители часто устанавливают под внутренними стенами и перегородками железобетонные тумбы.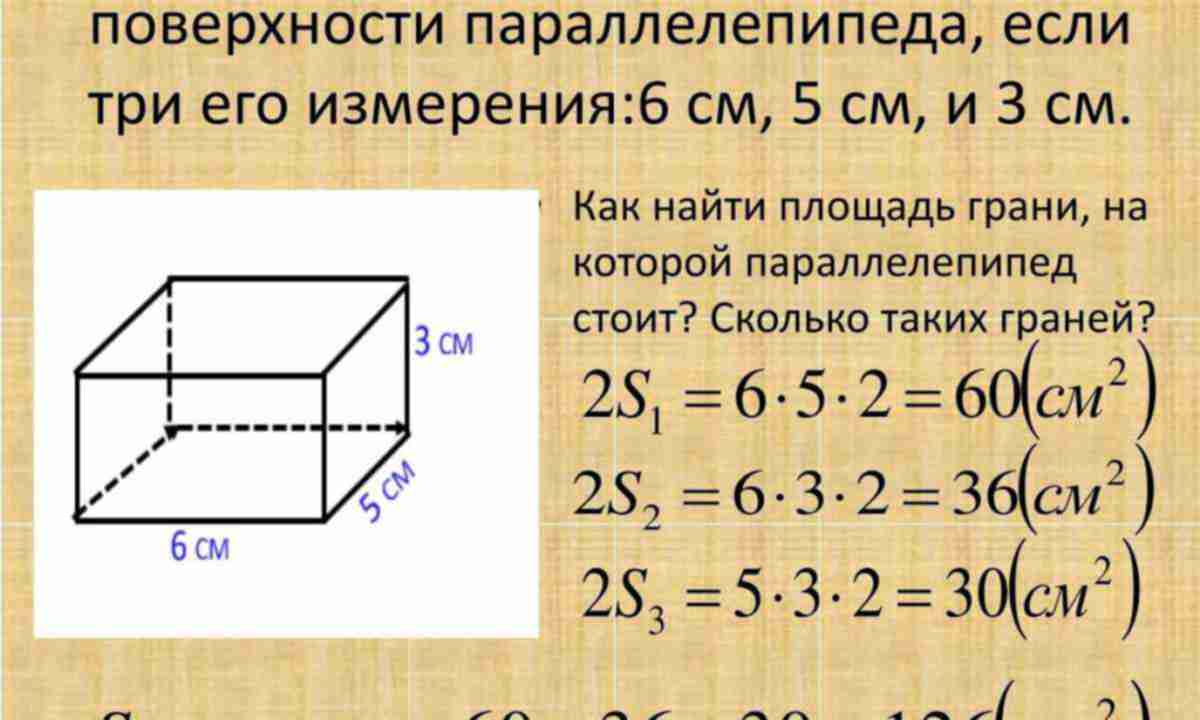 Их объем находят с помощью стандартной формулы:
Их объем находят с помощью стандартной формулы:
V=a*b*c, где:
- V – кубатура тумбы;
- a – ширина;
- b – высота;
- c – длина.
В соответствии со строительными нормами ленточные монолиты комплектуют системой вентиляции. Параметры вентиляционных колодцев вычисляют отдельно:
V=πR2h, где:
- V – размер колодца;
- π – число Пи;
- R2 – квадрат радиуса колодца;
- h – его глубина.
Радиус колодца – это половина его диаметра.
Общая кубатура сложного ленточного фундамента определяется путем сложения объемов всех частей конструкции:
Vобщ.= Vвнеш. к. + x(Vтумб) – x(Vколод), где:
- V общ – общий V конструкции;
- V внеш.к. – V внешнего контура;
- V тумб – V каждой тумбы;
- x – число тумб и вентиляционных отверстий;
- V колод –Vкаждого вентиляционного отверстия (колодца).

Расчет производится в метрах.
Вычисление размера плиты
Плита – монолитная заливка, площадь которой совпадает с площадью постройки. При возведении плитных фундаментов используются ребра жесткости. Они также учитываются в расчетах кубатуры.
Общая формула для монолита включает площадь (S) и толщину(H) плиты:
V=S*H, либо V=a*b*h, где:
- a – ширина основание;
- b – его длина;
- h – высота.
Она пригодна для вычисления кубатуры стен (за вычетом параметров оконных и дверных проемов), железобетонных перекрытий, бассейнов, подвалов, плитных оснований.
Объем ребер жесткости вычисляется по формуле для усеченной пирамиды:
- V – объем ребра жесткости;
- H – высота ребра;
- S1 – площадь нижнего основания;
- S2 – площадь верхнего основания.

Чтобы посчитать общие габариты плиты, известные объемы слагают.
Заливка пола
Стяжка пола – выравнивание поверхности с помощью бетонной смеси перед началом отделочных работ. Толщина стяжки варьируется от 4 до 10 см в зависимости от кривизны и дефектов пола. При относительно ровной поверхности расчет бетона производится по стандартной схеме.
В помещениях с неровными полами строители определяют объем заливки по усредненной высоте. При измерении стен, в комнате определяют точки минимальной(Hmin) и максимальной(Hmax) высоты. К величине перепада добавляют высоту стандартной заливки (4 см) и делят пополам:
Получив усредненную высоту пола, строители рассчитывают объем бетонной заливки по стандартной формуле.
Для получения точных расчетов принято использовать строительные калькуляторы. Зная параметры будущей конструкции, можно вычислить ее габариты и требуемое количество бетона.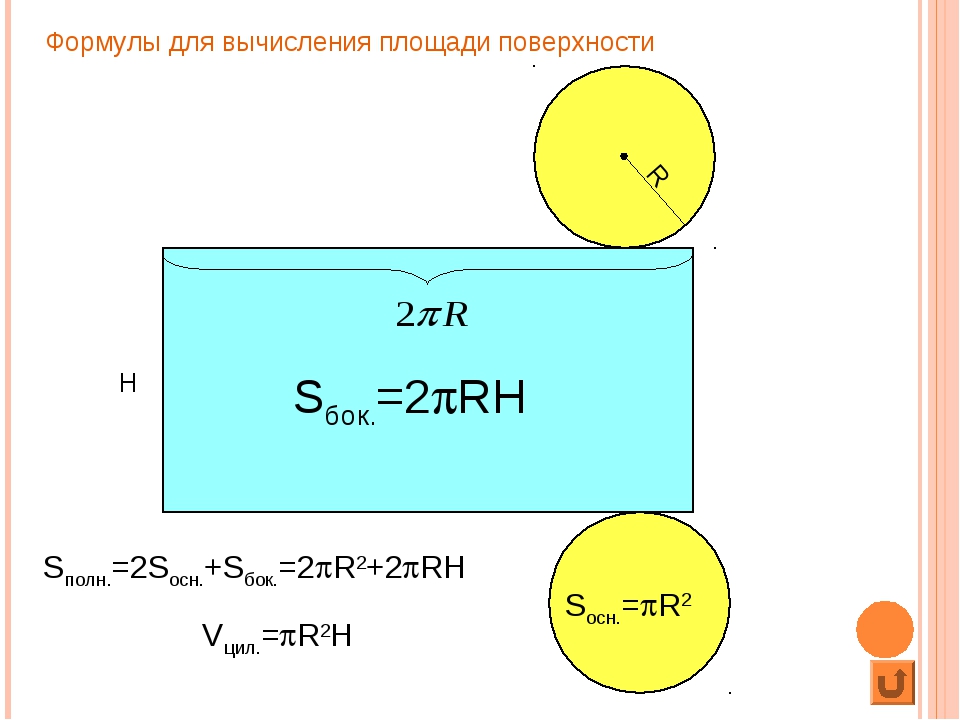 Армирующие элементы составляют от 5 до 10% от общих границ основания и не учитываются при расчетах. Традиционно данная погрешность нивелируется монтажными потерями при заливке материала.
Армирующие элементы составляют от 5 до 10% от общих границ основания и не учитываются при расчетах. Традиционно данная погрешность нивелируется монтажными потерями при заливке материала.
Смотрите также
Объем куба | Формула и как найти (видео)
Объем куба
Объем куба — это то, сколько места занимает куб в трех измерениях. Вы можете найти объем любого куба с одним заданным измерением, используя формулу объема куба :
.Объем куба всегда измеряется в кубических единицах, производных от линейных единиц, заданных или используемых для измерения длины стороны.
Содержание
- Объем куба
- Что такое куб?
- Формула объема куба
- Как найти объем куба
- Объем куба Примеры
Что такое куб?
Куб — это трехмерное тело с шестью равными квадратными гранями, пересекающимися под прямым углом, восемью вершинами и двенадцатью сторонами равной длины. Куб — одно из пяти Платоновых Тел, его также называют шестигранником.
Куб — одно из пяти Платоновых Тел, его также называют шестигранником.
Каковы размеры куба?
Куб — это трехмерный объект, поэтому куб имеет три измерения:
- Длина — Обычно считается большим из «плоских» размеров.
- Ширина — Обычно считается меньшим из «плоских» размеров.
- Высота или глубина — Измерение, которое привносит форму в наш трехмерный мир
Обратите внимание, у нас есть два способа описать третье измерение:
- Высота — Используйте этот термин, когда объект возвышается перед вами, как высокое здание.
- Глубина — Используйте этот термин, если объект падает под вами, как дыра в земле.
Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба.
Формула объема куба
Объем формулы куба — это объем, равный длине, умноженной на ширину, умноженной на высоту.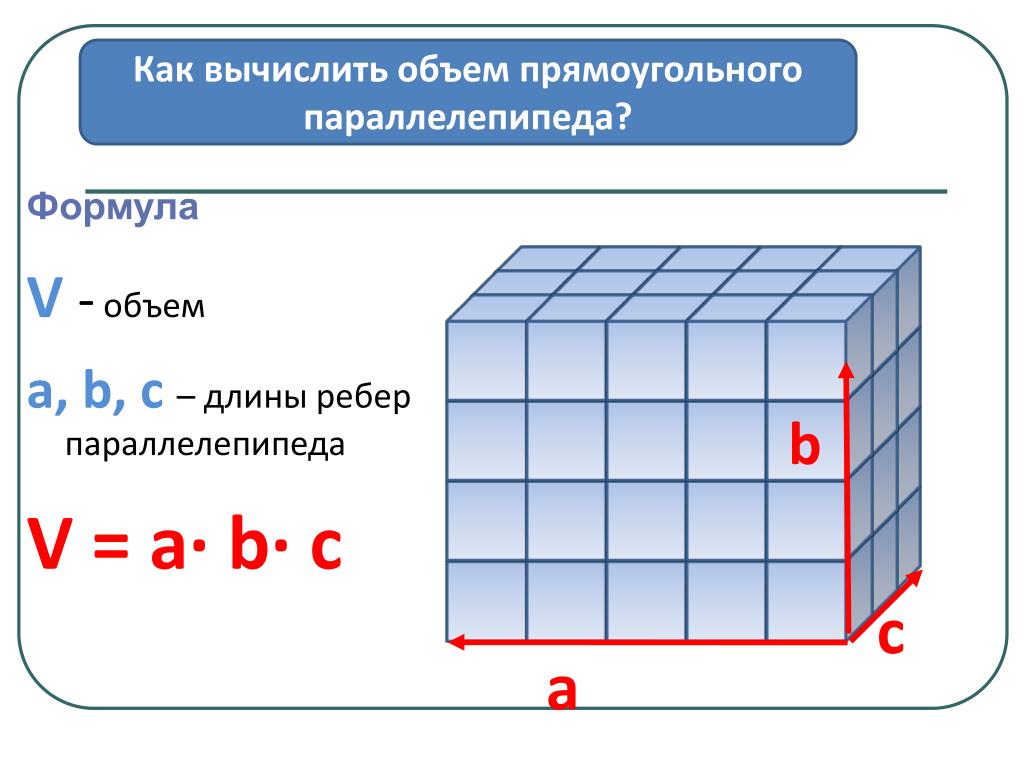
Это уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и кубоидов.
Поскольку все три значения — l, w и h — одинаковы в кубе, простейший объем формулы куба:
В этом объеме уравнения куба s = длина любого ребра.
Объем всегда измеряется в кубических единицах на основе предоставленных вам линейных единиц. Если вам говорят, что край куба составляет 3 метра, объем измеряется в кубических метрах или м3 (кубических метрах).
Как найти объем куба
Чтобы найти объем куба, вам нужно знать только длину любого ребра.
Если вам дана длина одной стороны, вы можете найти объем куба, подставив его в любую из формул объема для куба:
- V = д × ш × в
- В = s3
Чтобы измерить пространство, занимаемое кубом, нужно знать длину любого ребра, потому что все стороны куба равны по длине.
Как определить длину, ширину и высоту по объему
Что делать, если вам дан объем куба и попросят найти размеры куба?
Если вам дан объем куба и попросят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема:
Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах.
Что делать, если у нас есть куб, и нам говорят, что его объем составляет 729 кубических метров. Чтобы найти длину ребра куба:
с = 729 м33
s = 9 метров
Как рассчитать объем с использованием площади
Вот еще одна проблема. Что, если вам скажут площадь одной грани куба? Можете ли вы использовать эту информацию, чтобы найти объем?
Да, площадь одного лица равна длине лица, умноженной на ширину.Как только вы найдете ширину или длину, вы можете применить формулу объема:
- Найдите квадратный корень из заданного измерения площади; это даст вам длину любой стороны s.

- Используйте формулу объема V = s3, чтобы найти площадь
Как рассчитать площадь поверхности куба, используя объем
Если вам дан объем куба, вы можете преобразовать его в длину одной стороны. Затем вы можете использовать длину стороны для расчета общей площади поверхности.
Используйте длину ребра, чтобы вычислить площадь поверхности одной стороны, затем умножьте эту площадь на 6. Это даст вам общую площадь поверхности куба с учетом объема.
Что, если вам скажут, что общая площадь поверхности всего куба? Вы можете найти объем?
Да, общая площадь поверхности складывается из площади всех шести совпадающих граней. Найдите область одного лица, а затем выполните шаги, описанные выше, чтобы найти объем:
- Разделите заданную общую площадь поверхности на шесть, чтобы получить площадь одной грани
- Найдите квадратный корень из площади одной грани, чтобы получить длину любой стороны, s
- Используйте формулу объема, V = s3
Примеры объема куба
Если у вас есть трехмерное твердое тело с шестью гранями, стороны которого обозначены как 4 ‘, 6’ и 8 ‘. Это куб?
Это куб?
Нет, это прямоугольная призма, потому что этикетки, которые превосходят рисунок, имеют разную длину!
Что, если бы стороны нашего твердого тела были 4 ‘, 4’ и 4 ‘; это куб?
Это куб, потому что на этикетках указано, что ширина, длина и высота одинаковы.
Каков объем куба выше?
Вы записали V = 43?
Вы рассчитали V = 64 кубических фута, или фут3?
Давайте посмотрим на другой пример куба с длиной стороны 12 ярдов.Каков его объем?
В = с3
В = 123
V = 1728 кубических ярдов (ярд3)
А как насчет куба с одной гранью площадью 25 см. Каков объем куба?
Во-первых, какова длина любого ребра или стороны куба?
Подумайте: каков квадратный корень из 25? Ответ 5, значит:
s = 25 см
s = 5 см
Теперь, когда у вас есть длина стороны, вы можете рассчитать объем:
В = с3
В = 53
V = 125 кубических сантиметров, или
см3 Общая площадь куба составляет 7 776 квадратных дюймов (дюйм2). Каков объем куба?
Каков объем куба?
Помните, что общая площадь поверхности — это площадь всех шести квадратных граней. Разделите общую площадь поверхности на 6, извлеките из этого квадратный корень и воспользуйтесь формулой объема:
7776 дюймов26 = 1296 дюймов2
1296 дюймов2 = 36 дюймов
Теперь мы можем рассчитать объем куба:
В = 363
V = 46,656 кубических дюймов или 3 дюйм3
Следующий урок:
Что такое площадь поверхности
Общие сведения о площади поверхности и объеме
Наставник: Итак, если мы знаем, что можем найти площадь двумерной фигуры, вы думаете, что это можно ли найти площадь трехмерной фигуры? На самом деле, кто мне скажет, что за три размерная фигура есть?
Студент: Трехмерная фигура похожа на шар или куб — она не плоская.
Наставник: Верно. Теперь, может ли кто-нибудь сказать что-нибудь о том, что может означать обнаружение области такая цифра?
Студент: Когда вы говорите «найди местность», вы имеете в виду внешнее или внутреннее?
Наставник: Ну, это зависит от обстоятельств. На самом деле не существует такой вещи, как поиск «площади» куба. Вместо,
у нас есть термины «объем» и «площадь поверхности». Давайте сначала поговорим об объеме. Когда ты сказал
«Найди площадь» квадрата, ты имеешь в виду внешнюю сторону, или внутренности включены?
На самом деле не существует такой вещи, как поиск «площади» куба. Вместо,
у нас есть термины «объем» и «площадь поверхности». Давайте сначала поговорим об объеме. Когда ты сказал
«Найди площадь» квадрата, ты имеешь в виду внешнюю сторону, или внутренности включены?
Студент: Мы просто смотрим на место, которое он занимает на бумаге; мы предполагаем, что края квадрата имеют ширина нуля.
Наставник: Именно! А теперь представьте, сколько места занимает куб в трех измерениях. Мы назовем это мерой объема куба.
Студент: Как вы измеряете громкость?
Наставник: Так же, как вы измеряете и умножаете длину и ширину прямоугольника, чтобы найти его площадь, вы умножьте длину, ширину и высоту трехмерного объекта, например куба, чтобы найти его объем. В умножение трех переменных дает ему три измерения, таким образом, объем, а не просто область.Как вы думаете, какие единицы измерения объема?
Студент: Ну, если есть три члена, все в дюймах, тогда это будут дюймы * дюймы * дюймы,
что в дюймах в кубе.
Наставник: Чем это отличается от единиц, когда вы находите область?
Студент: Ну, площадь «возведена в квадрат», потому что вы просто умножаете дюймы на дюймы.
Наставник: Совершенно верно! Площадь «квадрат», а объем «куб».Как вы думаете, как это связано с их имея в виду?
Учащийся: Вы находите площадь квадрата или других двухмерных объектов, но обнаруживаете объем трехмерные объекты вроде кубиков!
Наставник: Хорошо, теперь мы знаем, как измерить, сколько места занимает объект. Но как насчет вне объекта, как вы упомянули ранее? Как вы думаете, что такое «площадь поверхности»?
Студент: Похоже, это были бы только внешние стороны — область, которая находится на поверхности, которую я могу трогать.
Наставник: Очень хорошо сказано! Площадь поверхности — это площадь поверхности трехмерной формы. Как вы бы посчитали что-нибудь подобное?
Студент: Это кажется слишком простым, но не мог бы я просто найти область каждого двухмерного лица, затем сложите области?
Наставник: Совершенно верно! Это так просто. Почти все трехмерные объекты, с которыми вы будете иметь дело, являются
состоящие из двухмерных граней, которые представляют собой просто квадраты, треугольники и т. д., и те, которые
изогнутые, как сферы, будут иметь свои особые формулы для площади поверхности.Конечно,
единицы для этого легко найти, не так ли?
Почти все трехмерные объекты, с которыми вы будете иметь дело, являются
состоящие из двухмерных граней, которые представляют собой просто квадраты, треугольники и т. д., и те, которые
изогнутые, как сферы, будут иметь свои особые формулы для площади поверхности.Конечно,
единицы для этого легко найти, не так ли?
Студент: Да, это просто стандартные единицы площади — единицы * единицы или единицы в квадрате.
Наставник: Понятно! Теперь вы готовы попытаться решить некоторые проблемы, связанные с площадью поверхности и объем.
математических формул для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм.Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур. Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь поверхности и объем сферы
Д. РасселТрехмерный круг известен как сфера. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ). Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. РасселКонус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь поверхности и объем цилиндра
Д. РасселВы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. РасселПрямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для этого вам нужно знать длину ( л ), высоту ( х ) и ширину ( х ). С кубом все три будут одинаковыми.
С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (левый) + 2 (левый) + 2 (белый)
- Объем = л. С.
Площадь и объем пирамиды
Д. РасселС пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно просто.
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 b 2 h
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д. Рассел
РасселПри переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину формы ( l ). Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих вычислений.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (бч) л
Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле используется высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = объявления
Площадь сектора круга
Д. Рассел Площадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах).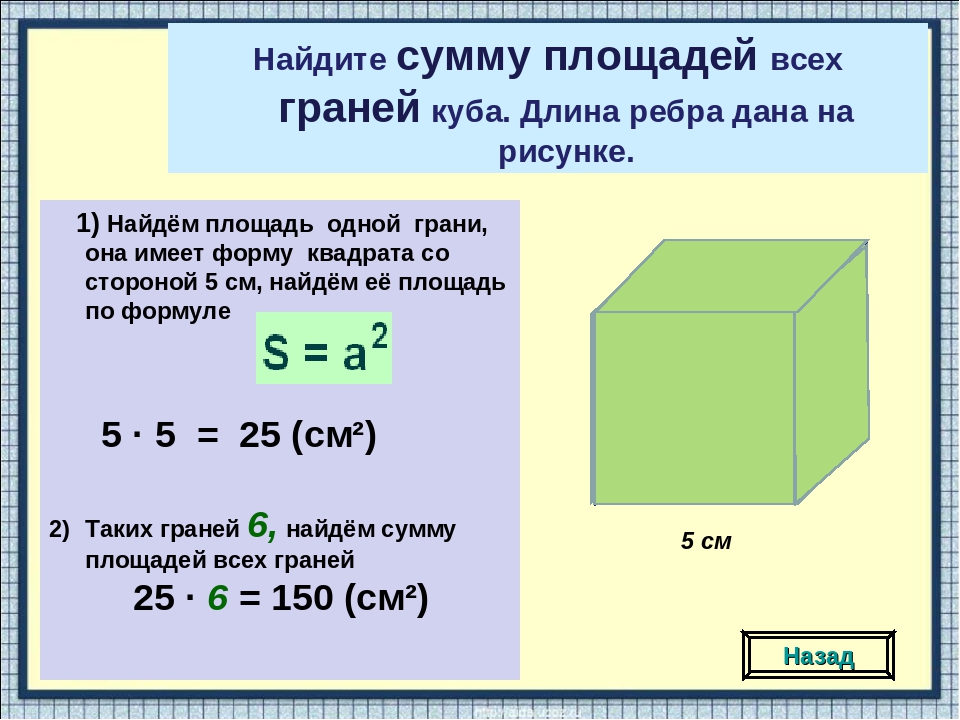 Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. РасселЭллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Полу-ось ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете увидеть эту формулу, записанную с r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам необходимо знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, который имеет одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ), это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были соединены как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник — это тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).
- Периметр = 2h + 2w
- Площадь = в x ш
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать только длину одной стороны ( с ), чтобы найти ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
Площадь поверхности и объем пирамид, призм, цилиндров и конусов (Геометрия, Площадь) — Mathplanet
Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела.Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.
Объем — это мера того, сколько фигура может вместить, и измеряется в кубических единицах. Объем говорит нам кое-что о вместимости фигуры.
Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть как прямоугольные, так и треугольные призмы.
Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем твердое тело, как картонную коробку, и расплющиваем его, чтобы найти все включенные геометрические формы.
Чтобы найти объем призмы (не имеет значения, прямоугольная она или треугольная), мы умножаем площадь основания, называемую площадью основания B, на высоту h.
$$ V = B \ cdot h $$
Цилиндр — это труба, состоящая из двух параллельных конгруэнтных окружностей и прямоугольника, основанием которого является окружность окружности.{2} \ cdot h $$
Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех- или четырехсторонней поверхности соответственно в основании. Когда мы вычисляем площадь поверхности пирамиды ниже, мы берем сумму площадей четырех треугольников и базового квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.
Объем пирамиды составляет одну треть объема призмы.
$$ V = \ frac {1} {3} \ cdot B \ cdot h $$
Основание конуса — круг, и это легко увидеть.{3}
$Видеоурок
Найдите площадь поверхности цилиндра радиуса 4 и высоты 8
Найдите объем конуса высотой 5 и радиусом 3
Узнайте о коробке
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторинг триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, What are the Retirement, Saving forSale price, CalculatingSc Scientific Notation, ConvertingSc Scientific Notation, DividingScaught Notation, MultiplyShapes, RectangleSimplifying, Thinking the ProductsSimplifying, Digimplifying, Something about aimplifer , Правые треугольники, Ветер, Рисунок
Как определить площадь поверхности и объем пирамид?
Как найти площадь поверхности пирамиды
Площадь поверхности фигуры 3D3D3D говорит нам о площадях всех разных сторон фигуры, суммированных вместе.В этой главе мы узнаем о площади поверхности и объемах пирамид. Есть много разных пирамид, таких как квадратная пирамида или прямоугольная пирамида. Итак, как нам найти площадь поверхности пирамиды? На самом деле есть формулы, которые помогут вам это найти.
Формула площади поверхности
Для обычной правой пирамиды, у которой все грани одинаковые, площадь поверхности = сумме всех площадей граней пирамиды.
Для квадратной пирамиды вам нужно вычислить площадь треугольника, используя: 12bs \ frac {1} {2} bs21 bs (для каждого треугольника, с которым вы работаете), затем найти площадь база.{2} SA = 2bs + b2
По сути, для обеих этих формул вы просто находите все площади с разных сторон пирамиды, а затем складываете их вместе, чтобы получить общую площадь поверхности. Вы можете представить сетку трехмерной формы разложенной, и вам необходимо рассчитать каждую из секций площади сетки отдельно.
как найти объем пирамиды
Объем показывает, сколько места занимает объект. Для пирамиды вы можете использовать приведенную ниже формулу, которая поможет вам найти ответ.
Формула для объема
Объем пирамиды = 13 \ frac {1} {3} 31 x (площадь основания) x hhh
Примеры задач
Вопрос:
Найдите площадь поверхности и объем
площадь и объем поверхностиРаствор:
Сначала ищем площадь поверхности (SA). Нам нужно будет найти площадь основания и четырех треугольных сторон. Для треугольных сторон нам не хватает высоты треугольника.{3} В = 24м3
Вопрос 2:
Найдите площадь поверхности и объем
Площадь и объем данного контейнераРаствор:
Мы начнем с поиска площади поверхности (SA). Перед этим нам нужно преобразовать неравные единицы и собрать необходимую информацию, которая нам не дана на графике.
Во-первых, нам нужны все числа в сантиметрах. Итак,
30 мм = 3 см 30 мм = 3 см 30 мм = 3 см
Затем нам нужно найти высоту треугольных сторон.{3} V = 2,24см3
Вы можете дополнительно исследовать объем треугольной пирамиды с помощью этого онлайн-калькулятора объема. Если вы готовы двигаться дальше, узнайте о площади поверхности и объеме других фигур и попробуйте решить несколько задач с объемными словами.
Оптимизация: использование расчетов для определения максимальной площади или объема
Оптимизация, или поиск максимумов или минимумов функции, является одним из первых приложений производной, которые вы изучите в математическом анализе в колледже.
В этом видео мы рассмотрим пример, в котором мы находим размеры загона (загона для животных), который максимизирует его площадь, с учетом ограничений по его периметру.Другие типы задач оптимизации, которые обычно возникают в расчетах:
- Увеличение объема коробки или другого контейнера
- Минимизация стоимости или площади поверхности контейнера
- Минимизация расстояния между точкой и кривой
- Минимизация времени производства
- Максимизация дохода или прибыли
В этом видео рассматриваются основные этапы выявления проблем оптимизации с ограничениями, создания уравнений и использования вычислений для решения оптимальных точек.


 м.
м. м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.
 2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту: 14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3 Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.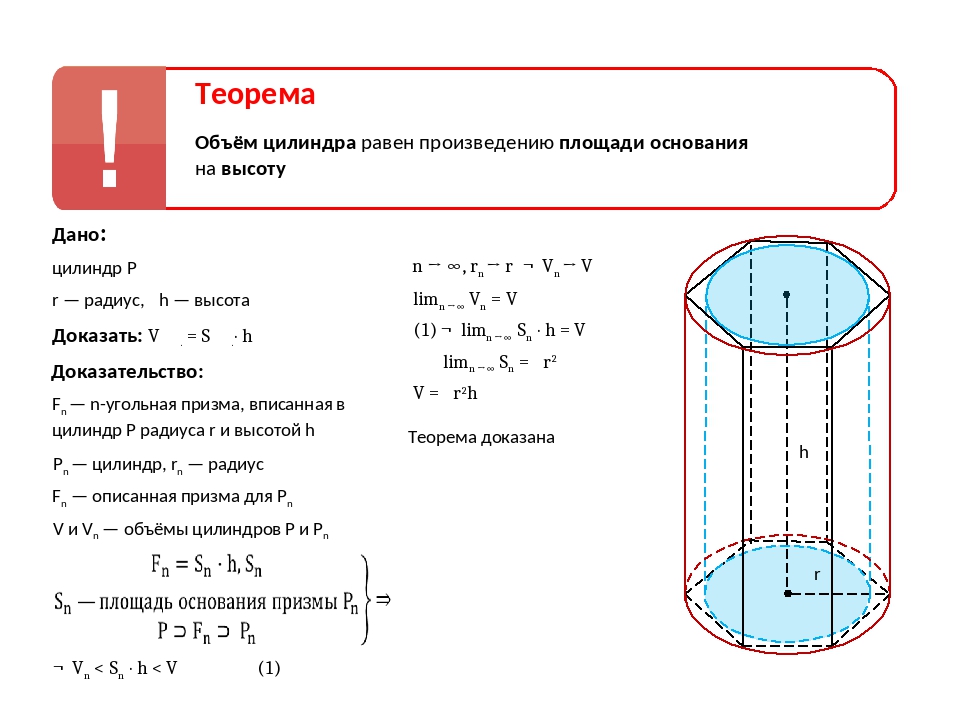

 ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/