Разность пятой степени | Формулы с примерами
1. 35 — 25 = (3 — 2) • (34 + 33 • 2 + 32 • 22 + 3 • 23 + 24) =
(3 — 2) • (81 + 27 • 2 + 9 • 4 + 3 • 8 + 16) =
1 • (81 + 54 + 36 + 24 + 16) =
1 • 211 = 211 ;
a = 35 ;
b = 25 ;
2. 45 — 35 = (4 — 3) • (44 + 43 • 3 + 42 • 32 + 4 • 33
(4 — 3) • (256 + 64 • 3 + 16 • 9 + 4 • 27 + 81) =
1 • (256 + 192 + 144 + 108 + 81) =
1 • 781 = 781 ;
a = 45 ;
b = 35 ;
3. 55 — 25 = (5 — 2) • (54 + 53 • 2 + 52 • 22 + 5 • 23 + 24) =
(5 — 2) • (625 + 125 • 2 + 25 • 4 + 5 • 8 + 16) =
3 • (625 + 250 + 100 + 40 + 16) =
3 • 1 031 = 3 093 ;
a = 55 ;
b = 25 ;
formula-xyz.ru
Многочлены | Формулы с примерами
Многочлен это?
Многочлен — это алгебраическая сумма одночленов.
Члены многочлена — это одночлены, составляющие многочлен.
Двучлен — многочлен, состоящий из двух членов.
Пример|
Двухчлен:
x + 15; 5a2b4 — a. |
Трехчлен — многочлен, состоящий из трех членов и т.д.
Пример|
Трехчлены:
7,4b2c + b — 6; x + y2 — xk. |
! Одночлен является частным случаем многочлена.
Стандартный вид многочлена
1. Приведены подобные.
Пример2. Все члены записаны в стандартном виде.
ПримерСтепень многочлена
Степень многочлена — наибольшая степень одночлена, входящего в многочлен.
Многочлен второй степени.
ПримерМногочлен третьей степени.
Примерformula-xyz.ru
Формулы разности и суммы степеней
В программу углубленного изучения математики входят две формулы, обобщающие общеизвестные, хрестоматийные формулы разности квадратов и кубов, а также суммы кубов.
Для любого натурального числа n:
$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}\times b+ a^{n-3}\times b^2+\ldots+ a^{2}\times b^{n-3}+ a\times b^{n-2}+b^{n-1}$
$a^{2k+1}+b^{2k+1}=(a+b)(a^{2k}-a^{2k-1}\times b+ a^{2k-2}\times b^2-\ldots -a^{2}\times b^{2k-2}- a\times b^{2k-1}+b^{2k}$
Они также входят в программу профильного курса математики. И мы уже видели, насколько полезными являются эти формулы для решения задач на делимость и остатки для натуральных и целых чисел.
Доказательство этих формул несложно, хотя и связано с техническими, достаточно простыми выкладками. Для формулы разности степеней оно получается на основе обязательной для всех формулы суммы геометрической прогрессии: достаточно лишь заметить, что в формуле разности степеней второй множитель в правой части является суммой n членов геометрической прогрессии с первым членом $b_{1}=a^{n-1}$ и знаменателем $q=\frac b a$. Поэтому он равен:
так что $(b-a)S=b^n-a^n$, а это и есть доказываемая формула.
А для доказательства формулы суммы нечетных степеней можно в доказанную формулу подставить -b вместо b и взять n=2к+1.
Применения этих формул к делимости целых и натуральных чисел основываются на их следствиях:
разность степеней двух натуральных или целых чисел с одинаковыми показателями делится на разность оснований;
сумма степеней двух натуральных или целых чисел с одинаковыми нечетными показателями делится на сумму оснований.
Помимо практических приложений, эти формулы полезны и для теории. С их помощью можно доказать в общем виде признаки делимости на 3 и на 9, которые в младших классах были «доказаны» на примерах, т.е., строго говоря, оставлены без доказательства.
В самом деле, натуральное число с с цифрами $a_{0},a_{1},a_{2},\ldots,a_{k-1},a_k$ в виде суммы разрядных слагаемых представляется как
$c=a_0\times10^k+a_1\times10^{k-1}+ a_2\times10^{k-2}+\ldots+ a_{k-1}\times10+a_k$
и, вычитая из с сумму его цифр
$s=a_{0}+a_{1}+a_{2}+\ldots+a_{k-1}+a_k$ получаем число
$c-s= a_0(10^k-1)+a_1(10^{k-1}-1)+ a_2(10^{k-2}-1)+\ldots+a_{k-1}(10-1)$
а поскольку всякое число вида $10^n-1$ записывается с помощью одних девяток, то c-s делится на 9, так что число и сумма его цифр при делении на 9 дают одинаковые остатки, и в частности, делятся или не делятся на 9 одновременно. То же самое рассуждение годится и для числа 3.
Заметим, что с использованием сравнений доказательство проводится в одну строчку: так как $10\equiv1 (\mod {9})$, то
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Одночлены | Формулы с примерами
Одночлен это?
Одночленом — называется произведение чисел, переменных и их натуральных степеней.
Пример| Одночлены: |
| Не одночлены: |
Стандартный вид одночлена
Стандартным видом одночлена называется произведение, составленное из числового множителя и степеней различных переменных.
Числовой множитель называется коэффициентом одночлена, его записывают перед буквенными сомножителями.
! Коэффициент равный 1 не записывается.
! При коэффициенте равному -1, записывается только «-» перед буквенными множителями.
Степень одночлена
Степенью одночлена называется сумма показателей степеней его буквенных множителей (переменных).
Пример| Степень одночлена 6x2y2c равна 2 + 2 + 1 = 5. |
| -1,4a2b5c3 — одночлен 10-ой степени, поскольку 2 + 5 + 3 = 10. |
! Если одночлен является нулевым числом, то его степень считается равной нулю.
Пример| 13; -2,3; 7; ?9 — Одночлены нулевой степени. |
! Одночлены, отличающиеся только числовыми коэффициентами, называются подобными.
Пример|
2ab и 3ab;
2x2 и -5x2; -9 и 6. |
formula-xyz.ru
§5.2. Конечные разности. Обобщенная степень.
Пусть задана функция 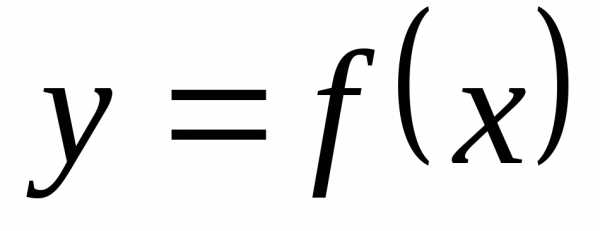 .
Обозначим через
.
Обозначим через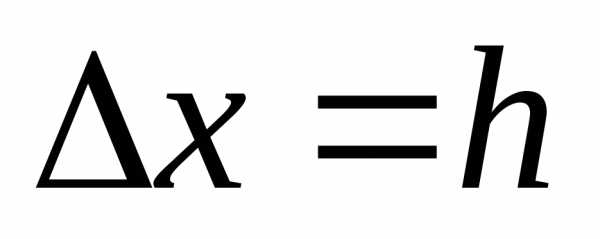 фиксированную величину приращения
аргумента (шаг). Тогда выражение
фиксированную величину приращения
аргумента (шаг). Тогда выражение
(5.3)
называется первой конечной разностью
функции 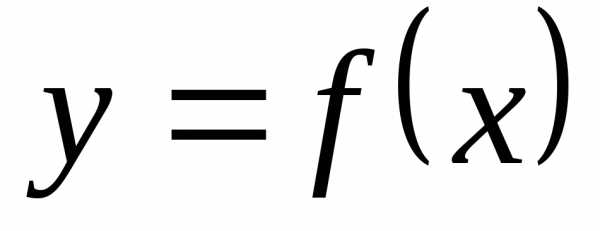 .
Аналогично определяются конечные
разности высших порядков
.
Аналогично определяются конечные
разности высших порядков
Например:
(5.4)
Символ  (дельта) можно рассматривать как оператор,
ставящий в соответствие функции
(дельта) можно рассматривать как оператор,
ставящий в соответствие функции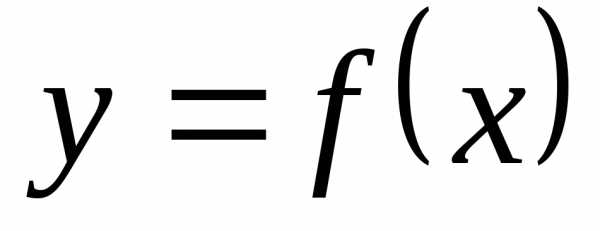 функцию.
функцию.
Легко проверить основные свойства
оператора  :
:
1) ;
2) ;
3)
,
где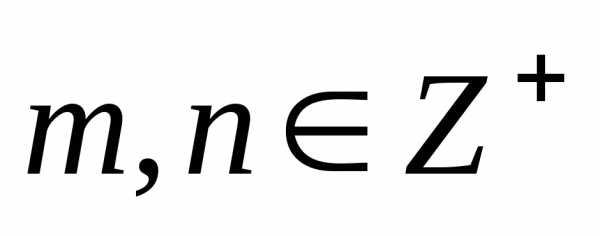 (целые неотрицательные числа), причем
(целые неотрицательные числа), причем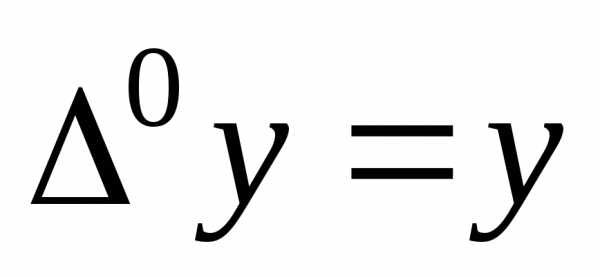 .
.
Из формулы (5.3) имеем:
.
Отсюда, рассматривая  как символический множитель, получим:
как символический множитель, получим:
. (5.5)
Из формулы (5.4):
; (5.6)
и т.д. Окончательно получим:
. (5.7)
В дальнейшем нам понадобится понятие обобщенной степени.
Определение.
Обобщенной 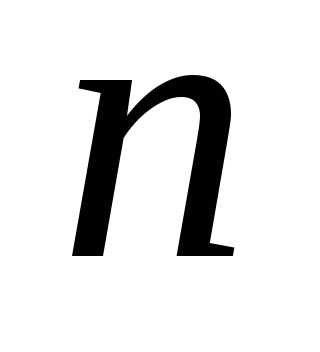 -степенью
числа
-степенью
числа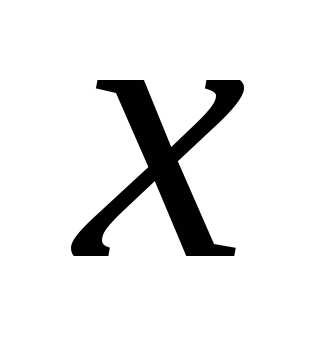 называется произведение
называется произведение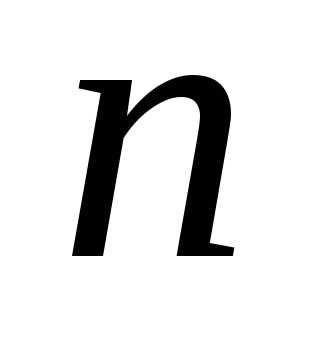 сомножителей, первый из которых равен
сомножителей, первый из которых равен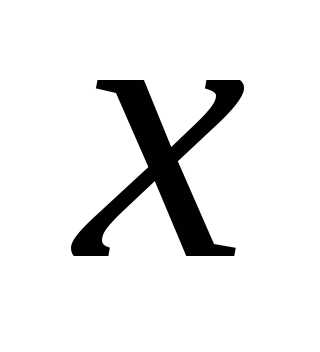 ,
а каждый следующий на
,
а каждый следующий на меньше предыдущего:
меньше предыдущего:
, (5.8)
где
.
Полагают, что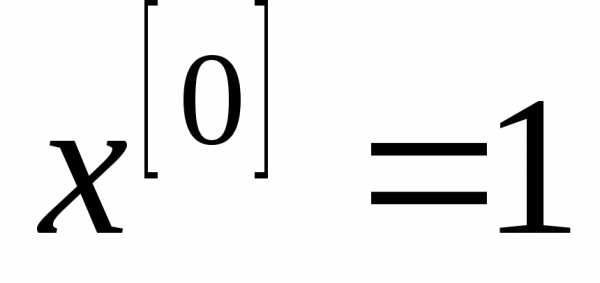 .
При
.
При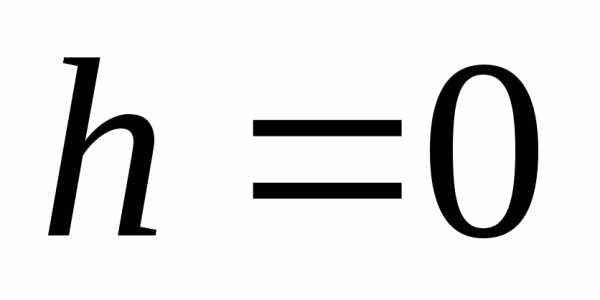 обобщенная степень совпадает с обычной:
обобщенная степень совпадает с обычной: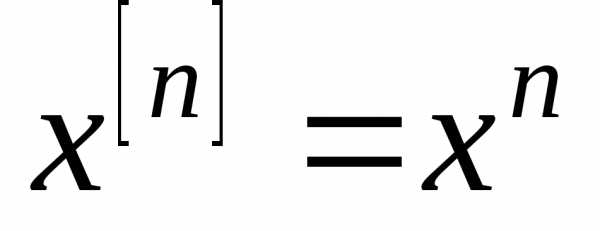 .
.
Вычислим конечные разности для обобщенной
степени, полагая 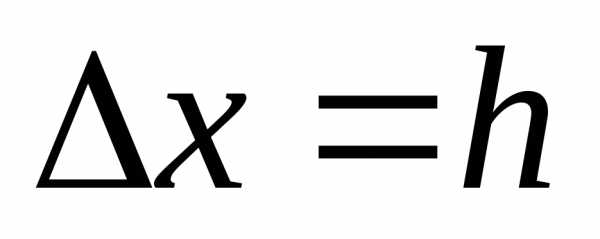 .
Для первой конечной разности имеем:
.
Для первой конечной разности имеем:
то есть
. (5.9)
Для второй конечной разности:
,
то есть
. (5.10)
Аналогично,
,
и так далее.
Окончательно будем иметь:
, (5.11)
,
если 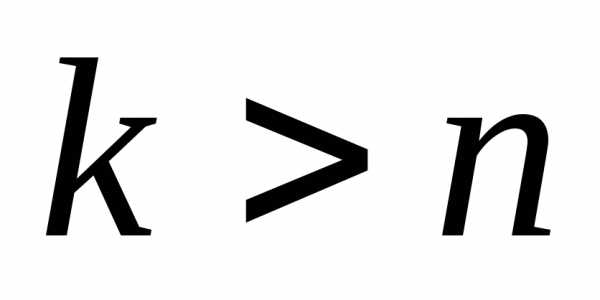 . (5.12)
. (5.12)
§5.3. Первая интерполяционная формула Ньютона.
Пусть для функции заданы значения
заданы значения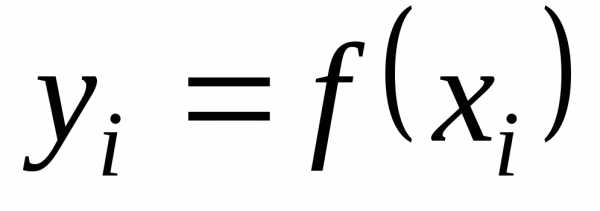 для равноотстоящих значений независимой
переменной,
где
для равноотстоящих значений независимой
переменной,
где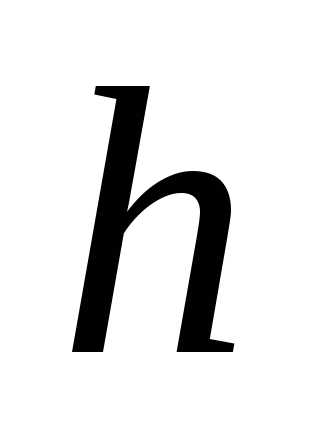 — шаг интерполяции. Требуется подобрать
полином
— шаг интерполяции. Требуется подобрать
полином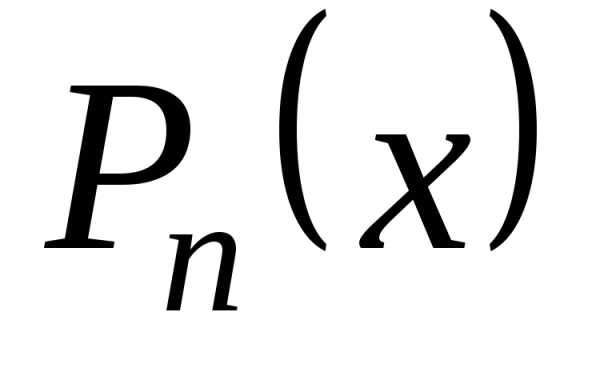 степени не выше
степени не выше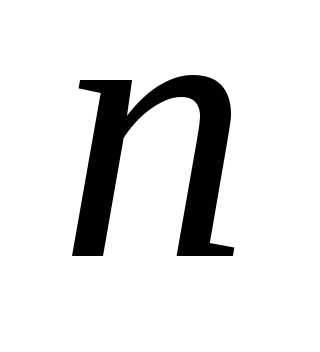 ,
принимающий в точках
,
принимающий в точках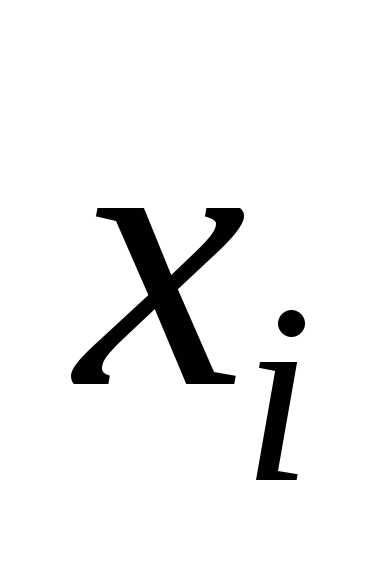 значения
значения. (5.13)
Условия (5.13) эквивалентны тому, что
. (5.14)
Будем искать полином в виде
. (5.15)
Используя понятие обобщенной степени, запишем выражение (5.15) в виде:
. (5.16)
Чтобы
полином был определен, нужно найти
коэффициенты 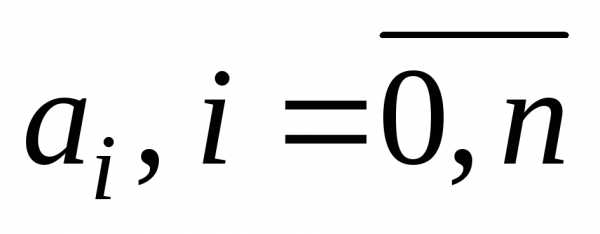
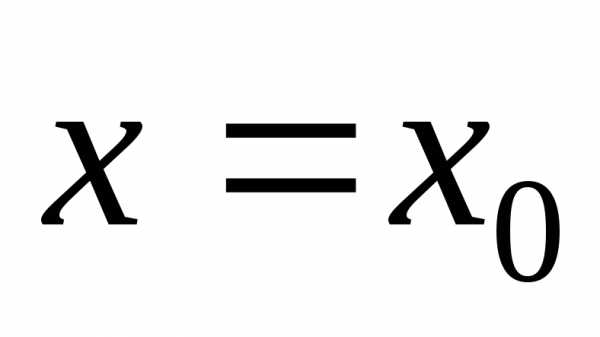 в выражении (5.16), получим
в выражении (5.16), получим. (5.17)
Чтобы
найти коэффициент 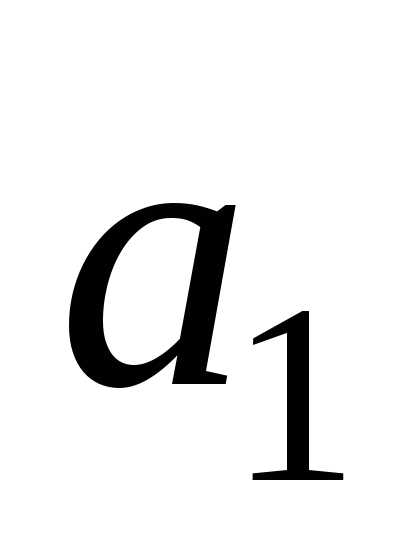 ,
составим первую конечную разность:
,
составим первую конечную разность:
.
Полагая 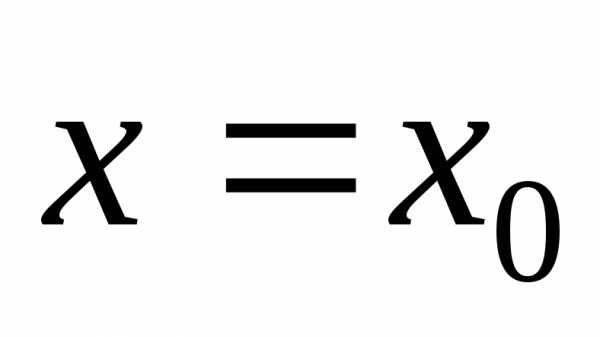 ,
получим:
,
получим:
,
откуда
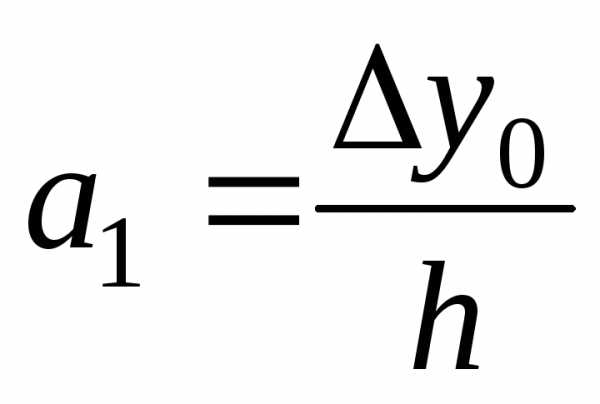 .
(5.18)
.
(5.18)
Для
определения коэффициента 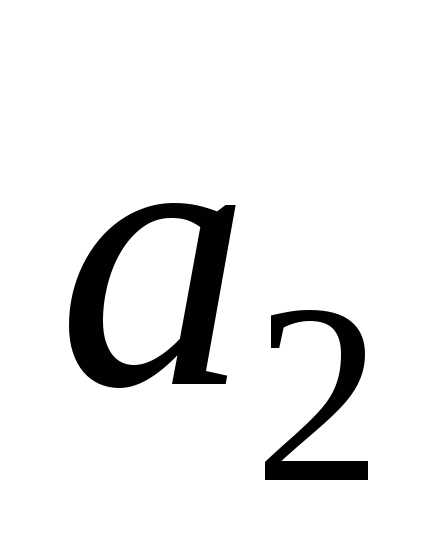 составим вторую конечную разность:
составим вторую конечную разность:
.
Положив 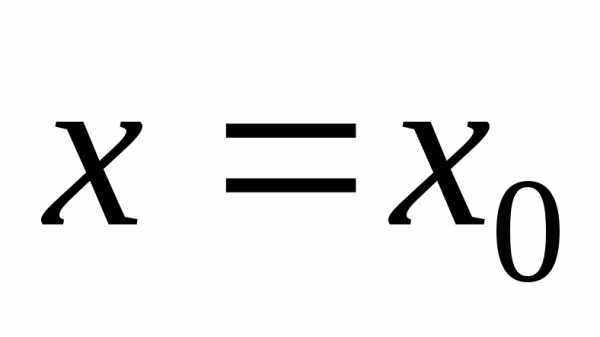 ,
получим:
,
получим:
,
откуда
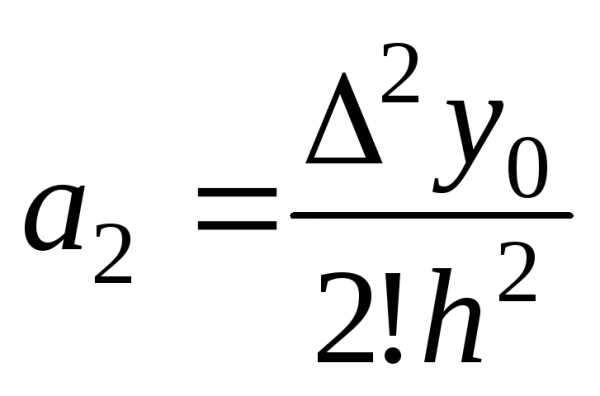
Продолжая процесс, получим:
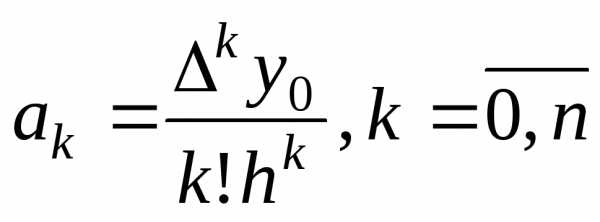 ,
(5.20)
,
(5.20)
причем .
Подставляя
найденные значения коэффициентов 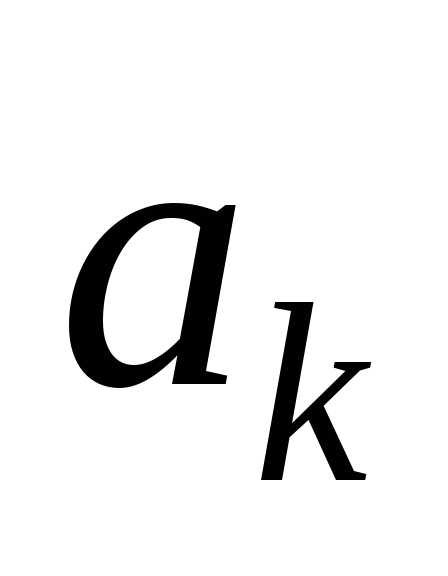 в выражение (5.16), получим интерполяционный
полином Ньютона:
в выражение (5.16), получим интерполяционный
полином Ньютона:
. (5.21)
Этот
полином полностью удовлетворяет
требованиям поставленной задачи.
Действительно, степень полинома 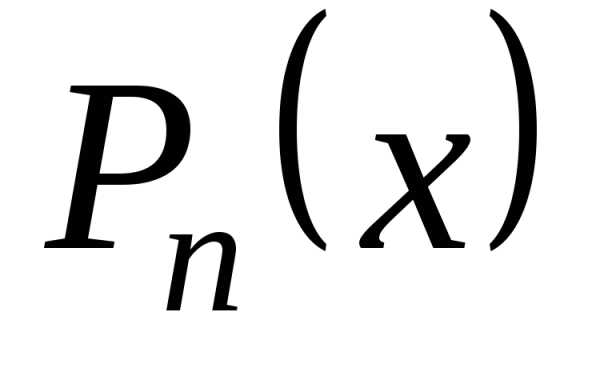 не выше
не выше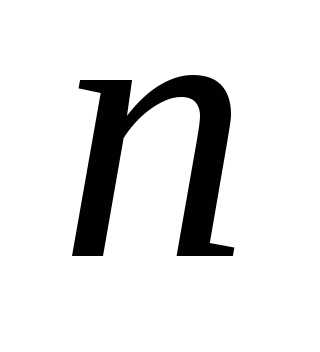 ;;
;;
Для практического использования первую интерполяционную формулу Ньютона записывают в несколько преобразованном виде. Для этого введем новую переменную
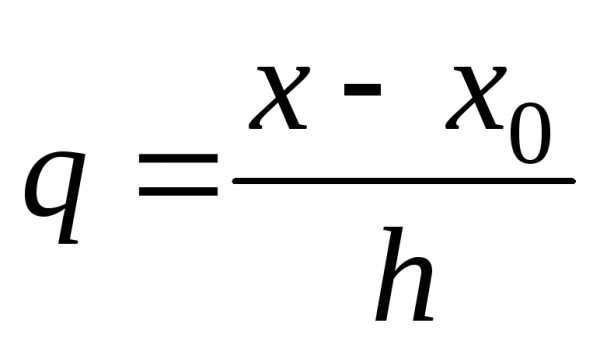
Тогда
(5.23)
Подставляя (5.23) в (5.21), получим окончательный вид первой интерполяционной формулы Ньютона:
. (5.24)
Если
в формуле (5.24) положить 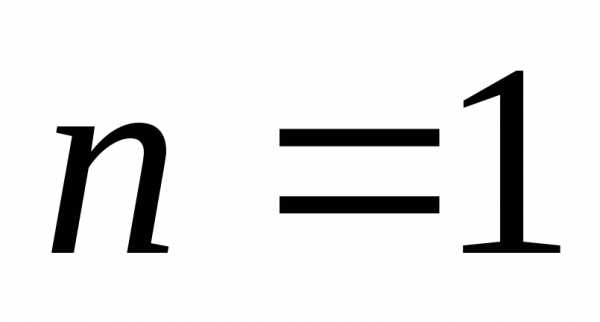 ,
то получим формулу линейного
интерполирования:
,
то получим формулу линейного
интерполирования:
. (5.25)
При  получим формулу параболического или
квадратичного интерполирования:
получим формулу параболического или
квадратичного интерполирования:
. (5.26)
Первую
интерполяционную формулу Ньютона
используют для интерполирования функции
в окрестности начальной точки 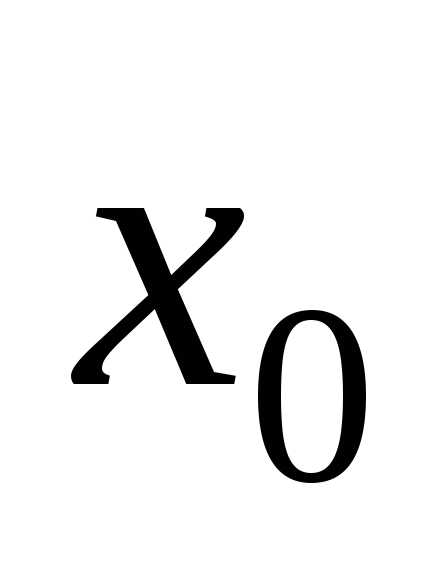 ,
где
,
где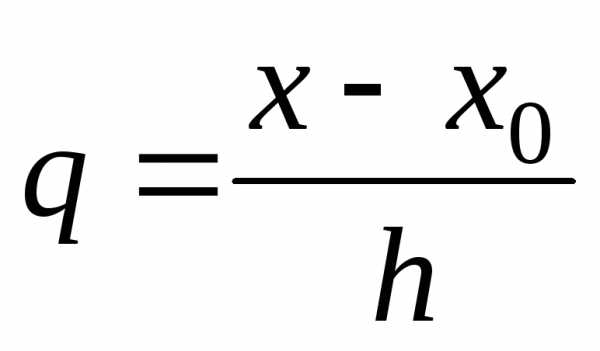 мало по абсолютной величине и представляет
собой число шагов, необходимых для
достижения точки
мало по абсолютной величине и представляет
собой число шагов, необходимых для
достижения точки
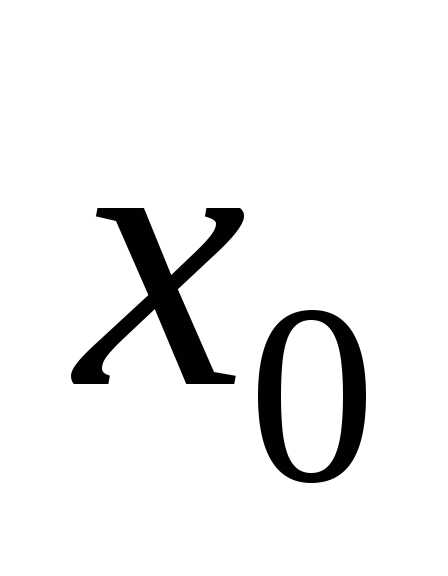 .
.Остаточный член первой интерполяционной формулы Ньютона:
, (5.27)
где  — некоторое промежуточное значение
между узлами интерполированияи рассматриваемой точкой
— некоторое промежуточное значение
между узлами интерполированияи рассматриваемой точкой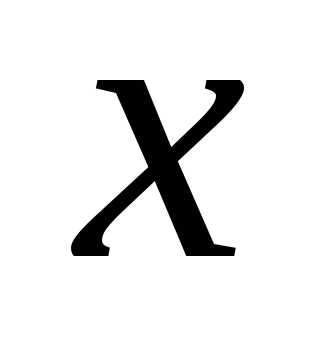 .
.
Учитывая, что , приближенно можно положить:
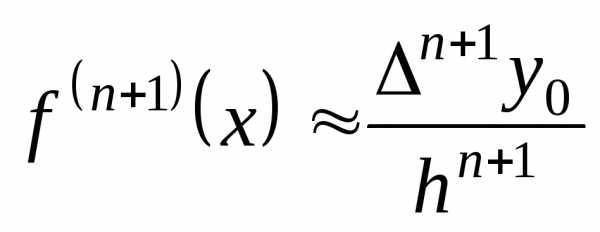 .
.
В этом случае соотношение (5.27) примет вид:
. (5.28)
studfiles.net
Степень с натуральным показателем | Формулы с примерами
Определение степени с натуральным показателем
Определение
где a — действительное число,
n — натурально число.
Читается как: «a в степени n» или
«n-ная степень a»
Калькулятор степени с натуральным показателем
Примеры и свойства
Свойство a в степени 1 равно a.a1 = a
Пример 11 = 1; 101 = 1; 1251 = 125.
Свойство Нуль в степени n равен нулю.0n = 0
Пример 10 = 0; 100 = 0; 4320 = 0.
Свойство Если a является положительным числом, то a возведенное в степеньn будет числом положительным.
Если a > 0, то an > 0
Пример 12> 0; 124 > 0; 332 > 0.
Свойство Если a является числом отрицательным, и его степень — четное число,то a в степени n будет число положительное.
Если a и n — четное, то an > 0
Пример (- 2)4 > 0; (- 33)6 > 0; (- 1,3)44 > 0.
Свойство Если a является числом отрицательным, и его степень — нечетное,то a в степени n будет число отрицательное.
Если a и n — нечетное, то an
Формулы по алфавиту:
© 2019 Все права защищеныПри использовании материалов данного сайта обязательно указывать ссылку на источник
formula-xyz.ru
