Физика. Волькенштейн В.С. Задача № 19.31
- Физика. Волькенштейн В.С.
- Физика атома и атомного ядра
- Квантовая природа света и волновые свойства частиц
- 19.31
Условие задачи 19.31:
Рентгеновские лучи с длиной волны λ0=20 пм испытывают комптоновское рассеяние под углом φ=90°. Найти изменение Δλ длины волны рентгеновских лучей при рассеянии, а также энергию We и импульс электрона отдачи.
Решение задачи:
СДЕЛАЙТЕ РЕПОСТ

Решение задачи 19.31
Предыдущая задача:
19.30 Рентгеновские лучи с длиной волны λ0=20 пм испытывают комптоновское рассеяние под углом φ=90°. Найти изменение Δλ длины волны рентгеновских лучей при рассеянии, а также энергию We и импульс электрона отдачи.Следующая задача:
19.32 Рентгеновские лучи с длиной волны λ0=20 пм испытывают комптоновское рассеяние под углом φ=90°. Найти изменение Δλ длины волны рентгеновских лучей при рассеянии, а также энергию We и импульс электрона отдачи. С другими задачами из решебника по физике Волькенштейна вы можете ознакомиться в соответствующем разделе решебника Физика. Волькенштейн В.С. studassistent.ru03 семестр / Разное / Пример курсача / Задача 2
Задача №2
В результате комптоновского рассеяния рентгеновских лучей с длиной волны λ=10 пм под некоторым углом θ к первоначальному пучку комптоновское смещение оказалось равным ∆λ=2,4 пм. Найти угол θ и величину энергии, переданной при этом электронам отдачи.
Дано: Решение
∆λ=2,4 пм
=2,4∙10-12 м
Решение
λ=10 пм
=1∙10-11 м
а) θ — ?
б)E — ?
Изменение длины волны рассеянного излучения в длинноволновую сторону спектра называется комптоновским смещением
(2.1)
где и — соответственно, длины волн до и после рассеяния;
— комптоновское смещение (2.2)
где 
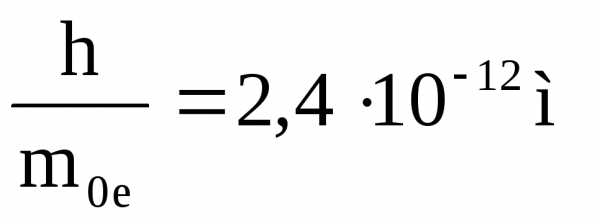 —
комптоновская длина волны
—
комптоновская длина волны
θ — угол рассеяния.
Из 2.2 найдем θ
;

б) По определению кинетическая энергия частицы в релятивистской механике
(2.3)
Используя закон сохранения энергии
(2.4)
таким образом получаем
(2.5)
Так как
 и
и 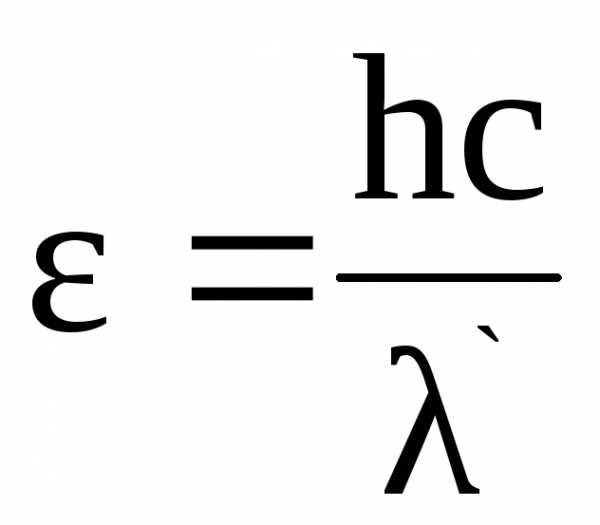 (2.6)
(2.6)
то подставив (2.6) в (2.5) получим
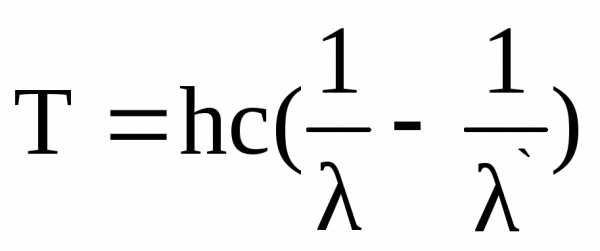
где
Подставим данные задачи
Ответ: а) θ = 90º
б) Е = 24 кэВ
13
studfiles.net
А6. В одном из опытов П.Н.Лебедева при падении света угол поворота крестовины, подвешенной
Решение (продолжение).
Теперь условие равновесия вертушки можно переписать так:
M -M ynp =0,
4( F1 — F2 ) L=kj.
Найдём силы давления F1 иF2:
F1 =p1S=(1+r1 ) Wc S=2Wc S. F2 =p2S=(1+r2 ) Wc S= Wc S.
F1 -F2 =2Wc S -Wc S =Wc S.
Подставим полученное выражение в условие равновесия:
А6. В одном из опытов П.Н.Лебедева при падении света угол поворота крестовины, подвешенной на упругой нити, был равенα = 10´. Найти световое давление и мощность падающего света. Диаметр кружкаd = 5 мм, расстояние от центра кружка до оси вращенияr = 9,2 мм, постоянная момента крученияk =
2,2·10-11 Н·м/рад.
|
| 4( F1- F2) | Решение (продолжение). | ||||||
|
| L =kj. | |||||||
|
|
|
|
| W | ||||
|
|
|
| F1- F2 | = c S. | ||||
|
|
|
| 4W SL=kj. | |||||
W =1 DE |
| c |
|
|
|
|
| ||
— | энергия, передаваемая единице площади поверхности тела | ||||||||
| S | Dt |
| излучением в единицу времени. | |||||
N =DE — |
| мощность излучения. | |||||||
| Dt |
|
| W = | 1 | DE = | N |
| |
|
|
|
|
|
| ||||
|
|
|
|
|
|
| |||
|
|
|
|
|
| S Dt S | |||

А6. В одном из опытов П.Н.Лебедева при падении света угол поворота крестовины, подвешенной на упругой нити, был равенα = 10´. Найти световое давление и мощность падающего света. Диаметр кружкаd = 5 мм, расстояние от центра кружка до оси вращенияr = 9,2 мм, постоянная момента крученияk =
2,2·10-11 Н·м/рад.
Решение (продолжение).
4Wc SL=kj. W =S1 DDEt =NS
4 cSN SL=kj.
Отсюда мощность излучения
N =ck4Lj.
| ckj | 3×108 ×2, 2×10- | 11 ×10×3,142 |
| — 4 | ( Bm). | |
N = |
| = | 4×9, 2×10- 3 | ×60×180 | »5,2×10 |
| |
4L |
| ||||||

А7. Найти световое давление на стенки электрической100-ваттнойлампы. Колба представляет собой сферический сосуд радиусомr = 5 см. Стенки лампы отражают 40% и пропускают 60% падающего на них света. Считать, что вся потребляемая мощность идёт на излучение.
Дано: |
|
|
|
|
|
|
| Решение. |
|
| ||
Давление | света на некоторую поверхность определяется | |||||||||||
ρ = 0,4 | ||||||||||||
формулой |
|
|
|
|
| |||||||
r = 5 cм |
| ( | 1+r | ) |
| |||||||
|
|
|
|
|
|
| c | |||||
N = 100 Вт |
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| P = |
| W . | |||
P — ? | W | = |
| 1 DE | — | энергия, | передаваемая единице площади | |||||
|
| S |
| Dt | поверхности тела излучением в единицу | |||||||
|
|
|
|
| времени. |
|
|
| ||||
Будем считать, что излучение, испускаемое лампой, распространяется вдоль радиусов сферической колбы лампы.
Энергия, излучаемая лампой D = D
E N t.
Площадь поверхности сферической колбы лампы
S =4pr2.
Подставим выражения для энергии излучения, площади поверхности сферы в формулу для давления света.
А7. Найти световое давление на стенки электрической100-ваттнойлампы. Колба представляет собой сферический сосуд радиусомr = 5 см. Стенки лампы отражают 40% и пропускают 60% падающего на них света. Считать, что вся потребляемая мощность идёт на излучение.
|
|
|
|
|
| Решение (продолжение). |
|
|
|
|
|
| |||||||||||||
P = 1+r | ) | W . | W = | 1 |
| DE | . DE =NDt. | S =4pr2. | |||||||||||||||||
S | Dt | ||||||||||||||||||||||||
( | c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
P = 1+r | ) | W | = | 1+r | 1 |
|
| DE = | ( | 1+r | ) | 1 |
| NDt | . | ||||||||||
c |
|
|
|
|
|
|
| ||||||||||||||||||
( |
|
| ( |
|
|
| ) ScDt |
|
|
| 4pr2cDt | ||||||||||||||
|
|
|
|
|
| P = 1+r |
|
|
| N | . |
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| ) 4pr2c |
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
| ( |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
P = 1+0, 4 |
|
|
|
|
|
|
| 100 |
|
|
| »15×10- 6 (Па). | |||||||||||||
) 4×3,14×25×10- 4 ××3 108 | |||||||||||||||||||||||||
| ( |
|
|
|
|
|
|
|
|
| |||||||||||||||
А8. Какова была длина волныλ0 рентгеновского излучения, если при
комптоновском рассеянии этого излучения графитом под углом θ = 60º длина волны рассеянного излучения оказалась равнойλ = 25,4 пм?
Дано: θ = 60º
λ = 25,4 пм
λ0 — ?
l 0 =l — L(
Решение.
Увеличение длины волны рассеянных фотонов при неупругом рассеянии на электронах (эффекте Комптона) определяется формулой: Dl =l — l 0 =L (1- cosJ ) ,
L =2ph | = | h | =2, 42×10- 12 | |
mc | ||||
mc |
|
| ||
l 0 =l | — L (1- cosJ ). | |||
1- cosJ ) =(25, 4 — 2, 42×(1- 0,5))×10- 12 » 24, 2×10- 12(м).

А9. Рентгеновские лучи с длиной волныλ = 20 пм испытывают комптоновское рассеяние под угломθ = 90º. Найти изменениеΔλ длины волны рентгеновских лучей при рассеянии, а также энергиюE и импульсp электрона отдачи.
Дано:
λ = 20 пм
θ = 90º
Δλ — ? p — ? E — ?
Решение.
Увеличение длины волны рассеянных фотонов при неупругом рассеянии на электронах (эффекте Комптона) определяется
формулой: | Dl=l | — l 0 =L(1- cosJ | ) , | ||
| |||||
| L =2ph = | h | =2, 42×10- 12(м). | ||
|
| ||||
| mc |
| mc |
| |
Dl =L(1- cosJ ) =2, 42×10- 12 (1- 0) | =2, 42×10- 12 (м). | ||||
В результате столкновения с фотоном электрон приобретает некоторую кинетическую энергию E и некоторый импульсp.
Кинетическую энергию электрона найдём из закона сохранения энергии. Закон сохранения энергии:

А9. Рентгеновские лучи с длиной волныλ = 20 пм испытывают комптоновское рассеяние под угломθ = 90º. Найти изменениеΔλ длины волны рентгеновских лучей при рассеянии, а также энергиюE и импульсp электрона отдачи.
|
|
| Решение (продолжение). |
|
|
| l ¢ l | ||||||||||||||
|
| c | h | c=h +1 |
|
| 1 |
|
|
|
| ||||||||||
|
|
|
| w |
|
| w¢E. |
|
|
|
|
| — |
| |||||||
E w w¢ |
|
|
|
|
|
|
|
| hc | æ |
| — |
|
| ö=hc | . | |||||
|
|
| — h |
|
|
|
|
|
|
|
| ||||||||||
=h — h = h | l |
| = |
| ç |
|
|
|
|
| ÷ |
| l l ¢ | ||||||||
| — |
| l ¢ |
|
| èl | D | l ¢ø |
| ||||||||||||
E =hc |
| l ¢ l |
| =hc |
|
|
|
| l |
|
|
|
| = |
|
| |||||
|
| l l ¢ | l | ( | l |
|
| l |
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| +D ) |
|
|
| |||||
=6,63×10- 34 ××3 108 ×2, 4×10- 12 =10,6×10- 16 (Дж) = 6,66 кэВ. 20×10- 12 ×22, 4×10- 12
Для определения импульса электрона воспользуемся релятивистской формулой для полной энергии.
А9. Рентгеновские лучи с длиной волныλ = 20 пм испытывают комптоновское рассеяние под угломθ = 90º. Найти изменениеΔλ длины волны рентгеновских лучей при рассеянии, а также энергиюE и импульсp электрона отдачи.
Решение (продолжение).
E +mc2 =c p2 +m2c2 .
E2+2Emc2+m2c4=c2p2+m2c4.
E2+2Emc2=c2p2.
Ec22 +2Em =p2.
p =Ec22 +2Em.

А10. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеянияθ = 90º. Найти энергиюE и импульсp рассеянного фотона.
Дано: |
|
|
|
|
|
|
| Решение. |
|
|
|
|
| ||||||
Eф = Eэ. | Согласно закону сохранения энергии при комптоновском рассеянии | ||||||||||||||||||
θ = 90º |
| E |
|
| m c2 |
| E¢ |
|
| E m c2 , |
| ||||||||
|
|
|
|
|
|
|
| ||||||||||||
E — ? |
|
| ph + | 0 | = | ph | + el | + | 0 |
| |||||||||
где Eph – энергия налетающего фотона,E´ph | – энергия рассеянного | ||||||||||||||||||
p — ? | |||||||||||||||||||
| фотона, Eel – кинетическая энергия электрона. |
| |||||||||||||||||
Согласно условию задачи |
| E¢ |
| E . | Поэтому | E | 2E¢. | ||||||||||||
|
|
|
| ph | = el |
|
|
|
|
|
|
| ph = | ph | |||||
|
|
|
|
|
| h | c |
| =2h | c | . |
|
|
|
| ||||
|
|
|
|
|
| l 0 |
|
|
|
|
| ||||||||
| 1 | 2 |
|
|
|
|
| l | l |
|
|
| |||||||
|
|
|
| = |
| , |
|
| l | 0 = |
| . |
|
|
| ||||
|
| l 0 |
| l |
|
|
|
|
| ||||||||||
|
|
|
|
| 2 |
|
|
| |||||||||||
Увеличение длины волны рассеянных фотонов при неупругом рассеянии на электронах (эффекте Комптона) определяется формулой:
Dl =l -l 0 =L(1- cosJ ) ,где L =2mcph =mch =2, 42×10- 12 (м).
studfiles.net
Физика. Рымкевич А.П. Задача № 1169
- Физика. Рымкевич А.П.
- Световые кванты. Действия света
- Фотоэлектрический эффект. Фотон. Давление света
- 1169
Условие задачи 1169:
Рентгеновские лучи с длиной волны 20 пм рассеиваются под углом 90°. Найти импульс электронов отдачи
Решение задачи:
СДЕЛАЙТЕ РЕПОСТ

Решение задачи 1169
Предыдущая задача:
1168 Рентгеновские лучи с длиной волны 20 пм рассеиваются под углом 90°. Найти импульс электронов отдачиСледующая задача:
1170 Рентгеновские лучи с длиной волны 20 пм рассеиваются под углом 90°. Найти импульс электронов отдачи С другими задачами из решебника по физике Рымкевича А.П. 10-11 класс вы можете ознакомиться в соответствующем разделе решебника Физика. Рымкевич А.П.studassistent.ru
