Решение алгебраических – —

ax^2k + bx^2k–1 + cx^2k–2 + dx^2k–3 + … + dx³ + cx² – bx + a = 0, которое называется возвратным (или симметрическим) уравнением степени 2k второго рода. Решается подстановкой

Пример 5. Решить уравнение 8x⁴ – 42x³ + 29x² + 42x + 8 = 0.

Ответ:

Возвратное уравнение нечетной степени имеет корень – 1. Это объясняется тем, что уравнение имеет четное число членов, которые при замене

Пример 6. Решить уравнение 24x⁵ + 74x⁴ – 123x³ – 123x² + 74x + 24 = 0.

Имеем возвратное уравнение 5-й степени. Один из его корней – 1. После деления на x + 1, получим

24x⁴ + 50x³ – 173x² + 50x + 24 = 0

Ответ:

если , то

По биному Ньютона

Замечание 2. Определить по внешнему виду, что уравнение является возвратным не всегда просто, особенно, если . Поэтому в уравнении степени 2n производим почленное деление на xⁿ и, если при этом получается сумма выражений вида , где n = 0, 1, 2 … m, то дальнейшее решение ясно.

Приложение

19.03.2007

xn--i1abbnckbmcl9fb.xn--p1ai

алгебраическое решение — это… Что такое алгебраическое решение?

• алгебраическое расширение
• алгебраическое свойство

Смотреть что такое «алгебраическое решение» в других словарях:

• решение — сущ., с., употр. часто Морфология: (нет) чего? решения, чему? решению, (вижу) что? решение, чем? решением, о чём? о решении; мн. что? решения, (нет) чего? решений, чему? решениям, (вижу) что? решения, чем? решениями, о чём? о решениях 1. Решением …   Толковый словарь Дмитриева

• АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ — уравнение вида где многочлен n й степени от одного или нескольких переменных . А. у. с одним неизвестным наз. уравнение вида: Здесь п целое неотрицательное число, наз. коэффициентами уравнения и являются данными, хназ. неизвестным и является… …   Математическая энциклопедия

• Алгебраическое уравнение —         уравнение, получающееся при приравнивании двух алгебраических выражений (См. Алгебраическое выражение). А. у. с одним неизвестным называется дробным, если неизвестное входит в знаменатель, и иррациональным, если неизвестное входит под… …   Большая советская энциклопедия

• Решение уравнения — Уравнение равенство вида или , где f и g функции (в общем случае векторные) одного или нескольких аргументов, а также задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут… …   Википедия

• решение — я; ср. 1. к Решить решать (кроме 6 зн.). Участвовать в решении чьей л. судьбы. Перенести срок решения вопроса. Оригинальное инженерное р. здания. Алгебраическое р. задачи. 2. Обдуманное намерение сделать что л., заключение, вывод из чего л.… …   Энциклопедический словарь

• решение — я; ср. 1) к решить решать Участвовать в решении чьей л. судьбы. Перенести срок решения вопроса. Оригинальное инженерное реше/ние здания. Алгебраическое реше/ние задачи. 2) Обдуманное намерение сделать что л., заключение, вывод из чего л …   Словарь многих выражений

• Кольцо алгебраическое — Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных …   Большая советская энциклопедия

• Алгебра —          Общие сведения          Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… …   Большая советская энциклопедия

• Вертикальные углы — Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая  из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух …   Википедия

• АЛГЕБРАИЧЕСКИЙ — АЛГЕБРАИЧЕСКИЙ, алгебраическая, алгебраическое. прил. к алгебра. Алгебраическая задача. Алгебраическое решение. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

• Якоби Карл Густав Яков — (Jacobi, 1804 1851) один из знаменитых германских математиков прошлого столетия, родился в Потсдаме. Первоначальное обучение получил под руководством своего дяди по матери, затем учился в тамошней гимназии и 16 ти лет от роду поступил в… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

dic.academic.ru

Алгебраическое решение — Большая Энциклопедия Нефти и Газа, статья, страница 1

Алгебраическое решение

Cтраница 1

Алгебраические решения получаются не иначе, как через уравнения.  [1]

Алгебраические решения могут быть найдены следующим образом.  [2]

Алгебраическое решение, а также решение тепловых и материальных балансов по высоте колонны и по ее частям представляют собой наиболее общий подход к расчету процесса ректификации. Для полного решения полученных уравнений данных обычно недостаточно. Поэтому программы такого типа решаются методом проб и ошибок.  [3]

Алгебраическое решение этой системы затруднительно.  [4]

Алгебраическое решение геометрических задач заключается в следующем. По условию задачи составляются уравнения ( неравенства), связывающие известные и неизвестные элементы фигур. Затем определяются те элементы или отношения между ними, которые требуется найти.  [5]

Алгебраическое решение системы узловых и контурных уравнений магнитной цепи обычными способами невозможно, так как эта система нелинейная. Поэтому в практике применяют графические и графоаналитические методы расчета разветвленных магнитных цепей.  [6]

Вместо алгебраического решения характеристического уравнения ( 1) можно использовать графический способ, известный под названием круга Мора, позволяющий находить компоненты тензора второго ранга в пространстве двух измерений и в произвольной системе ортогональных осей координат ( напряжения или деформации в точке, моменты инерции площадей плоских фигур, кривизны нормальных сечений поверхности и пр. Круг Мора дает графическую интерпретацию линейного преобразования любой симметричной матрицы или квадратичной формы второго ранга при повороте осей и, в частности, может служить для решения векового уравнения второй степени.  [7]

Здесь приводится алгебраическое решение эпиграммы о Диофанте.  [8]

Рассмотрим примеры обобщенных алгебраических решений.  [9]

Теоремы об алгебраических решениях и соответствии особенностей сводят задачу описания динамики абелевой области к задаче решения системы уравнений на параметры абелевых областей фиксированной степени.  [10]

В этом относительно простом случае алгебраическое решение все же можно получить, но обычно при большем числе компонентов и большем числе уравнений такой метод, как правило, непригоден.  [11]

Этот ступенчатый графический прием равнозначен повторяющемуся алгебраическому решению соответствующего кинетического уравнения. Простота построения наглядно изображает картину изменения концентраций по ходу каскада.  [13]

Приведенный алгоритм, основанный на алгебраическом решении системы уравнений ( 2 — VI), обладает достаточно быстрой сходимостью. Однако он довольно громоздок и трудоемок в программировании и отладке.  [14]

К самостоятельным достижениям Леонардо Фибоначчи относится приближенное алгебраическое решение кубического уравнения.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Решения алгебраических задач — Решения алгебраических задач на ЕГЭ по математике

Доступные файлы (1):

1.rtf

Применение метода тригонометрической подстановки при решении задач

Решение уравнений

Иррациональные уравнения

Рациональные уравнения

Показательные уравнения

Решение систем

Доказательство неравенств

Задачи на нахождение наибольшего и наименьшего значений

функции

Решение задач с параметрами
Метод замены переменной при решении задач

Переход к новым обозначениям, замена неизвестных – существенный прием и метод, который применяется при решении самых различных задач как элементарной, так и высшей математики. Очень важно, чтобы этот прием и метод был прочно усвоен и освоен в школе, так как идея замены переменной является сквозной и в том или ином виде фигурирует практически во всех разделах школьной математики.

Существуют два подхода к определению метода замены переменной. Если уравнение удалось преобразовать к виду , то нужно ввести новую переменную , решить уравнение , а затем рассмотреть совокупность уравнений

где – корни уравнения . Чтобы при замене не потерять корней, достаточно убедиться, что каждому значению из рассматриваемой области соответствует хотя бы одно значение , удовлетворяющее равенству .

В отличие от описанного выше метод равносильной замены требует нахождения множества значений переменной . В данном случае накладывается требование: каждому значению из рассматриваемой области соответствует ровно одно значение переменной , удовлетворяющее равенству . Такой подход ведет к сохранению области определения исходного уравнения и не требует перехода к совокупности.

Подобные замены порой существенно упрощают решение. Замена переменных и переход к новым обозначениям облегчают выкладки и делают громоздкое алгебраическое выражение компактным и обозримым. Вот почему следует приучать школьников при решении задач не торопиться начинать преобразования: пусть они сначала посмотрят, нельзя ли записать уравнение проще, введя новую переменную. При этом не стоит забывать, что, во-первых, далеко не всегда замена бывает столь уж необходима. Во-вторых, если приходится прибегать к замене неизвестной, то стоит сразу подобрать ее так, чтобы она вбирала в себя по возможности большее количество неприятных деталей, затрудняющих решение.

^

1. 
   Иррациональные уравнения
   

Пример 1. Решите уравнение

[12].

Решение с помощью тригонометрической подстановки

Так как , то . Поэтому можно положить . Уравнение примет вид

.

Положим , где , тогда

.

.

.

Ответ: .

Алгебраическое решение

.

Так как , то . Значит, , поэтому можно раскрыть модуль

.

Ответ: .

Решение уравнения алгебраическим способом требует хорошего навыка проведения тождественных преобразований и грамотного обращения с равносильными переходами. Но в общем оба приема решения равноценны.

Пример 2. Решите уравнение

[14].

^

Область определения уравнения задается неравенством , что равносильно условию , тогда . Поэтому можно положить . Уравнение примет вид

.

Так как , то . Раскроем внутренний модуль

.

Положим , тогда

.

Условию удовлетворяют два значения и .

.

.

Ответ: .

^

.

Возведем в квадрат уравнение первой системы совокупности, получим

.

Пусть , тогда . Уравнение перепишется в виде

.

Проверкой устанавливаем, что – корень, тогда делением многочлена на двучлен получаем разложение правой части уравнения на множители

.

От переменной перейдем к переменной , получим

.

Условию удовлетворяют два значения

.

Подставив эти значения в исходное уравнение, получаем, что – корень.

Решая аналогично уравнение второй системы исходной совокупности, находим, что тоже корень.

Ответ: .

Если в предыдущем примере алгебраическое решение и решение с помощью тригонометрической подстановки были равноценны, то в данном случае решение подстановкой выгоднее. При решении уравнения средствами алгебры приходится решать совокупность из двух уравнений, то есть дважды возводить в квадрат. После этого неравносильного преобразования получаются два уравнения четвертой степени с иррациональными коэффициентами, избавиться от которых помогает замена. Еще одна трудность – проверка найденных решений подстановкой в исходное уравнение.

Пример 3. Решите уравнение

[31].

^

Так как , то . Заметим, что отрицательное значение неизвестного не может быть решением задачи. Действительно, преобразуем исходное уравнение к виду

.

Множитель в скобках в левой части уравнения положительный, правая часть уравнения тоже положительная, поэтому множитель в левой части уравнения не может быть отрицательным. Вот почему , тогда , поэтому можно положить Исходное уравнение перепишется в виде

.

Так как , то и . Уравнение примет вид

.

Пусть . Перейдем от уравнения к равносильной системе

.

Числа и являются корнями квадратного уравнения

.

.

Ответ: .

Алгебраическое решение

Возведем обе части уравнения в квадрат

.

Введем замену , тогда уравнение запишется в виде

.

Второй корень является лишним, поэтому рассмотрим уравнение

.

Так как , то .

Ответ: .

В данном случае алгебраическое решение в техническом плане проще, но рассмотреть приведенное решение с помощью тригонометрической подстановки следует обязательно. Это связано, во-первых, с нестандартностью самой подстановки, которая разрушает стереотип, что применение тригонометрической подстановки возможно лишь, когда . Оказывается, если тригонометрическая подстановка тоже находит применение. Во-вторых, представляет определенную трудность решение тригонометрического уравнения , которое сводится введением замены к системе уравнений. В определенном смысле эту замену тоже можно считать нестандартной, а знакомство с ней позволяет обогатить арсенал приемов и методов решения тригонометрических уравнений.

Пример 4. Решить уравнение

[4].

Решение с помощью тригонометрической подстановки

Так как переменная может принимать любые действительные значения, положим . Тогда

,

,так как .

Исходное уравнение с учетом проведенных преобразований примет вид

.

Так как , поделим обе части уравнения на , получим

.

Пусть , тогда . Уравнение примет вид

.

.

Учитывая подстановку , получим совокупность из двух уравнений

.

Решим каждое уравнение совокупности по отдельности.

1) .

.

не может быть значением синуса, так как для любых значений аргумента.

.

Откуда

.

Так как и правая часть исходного уравнения положительна, то . Из чего следует, что .

2) .

.

Это уравнение корней не имеет, так как .

Итак, исходное уравнение имеет единственный корень

.

Ответ: .

^

Данное уравнение легко «превратить» в рациональное уравнение восьмой степени возведением обеих частей исходного уравнения в квадрат. Поиск корней получившегося рационального уравнения затруднен, и необходимо обладать высокой степенью изобретательности, чтобы справиться с задачей. Поэтому целесообразно знать иной способ решения, менее традиционный. Например, подстановку , предложенную И. Ф. Шарыгиным [57].

Положим , тогда

Преобразуем правую часть уравнения :

.

С учетом преобразований уравнение примет вид

.

Введем замену , тогда

.

Второй корень является лишним, поэтому , а .

Ответ: .

Если заранее не известна идея решения уравнения , то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени , найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения , если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.

Подчеркнем, что применение тригонометрической подстановки для решения задач должно быть осознанным и оправданным. Использовать подстановку целесообразно в тех случаях, когда решение другим способом сложнее или вовсе невозможно. Приведем еще один пример, который, в отличие от предыдущего, проще и быстрее решается стандартным способом.

Пример 5. Решить уравнение

[51].

^

Так как переменная может принимать любые действительные значения, можно положить . Уравнение примет вид

.

В силу того, что , можно раскрыть модуль

.

Так как , то .

Ответ: .

Алгебраическое решение

Проверкой убеждаемся, что – корень.

Ответ: .

^

Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.

При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.

Пример 1. Сколько корней имеет уравнение

[37].

Решение этой задачи любым методом начинается одинаково. Докажем, что все корни данного уравнения принадлежат промежутку . Действительно, если

.

Но тогда в исходном уравнении слева стоит произведение больше восьми, а справа единица, что невозможно.

^

Положим . Тогда каждому корню исходного уравнения будет соответствовать ровно один корень , где . Наоборот, каждому корню уравнения соответствует ровно один корень исходного уравнения. Таким образом, задача может быть переформулирована так: сколько корней на промежутке имеет уравнение

.

Так как и , то можно взять . Заметим, что если — корень данного уравнения, то и тоже корень. Вот почему достаточно рассмотреть , то есть отыскать только положительные решения. С учетом выше изложенного исходное уравнение перепишется в виде

.

Так как , то можно обе части равенства умножить на , получим

.

Ответ: шесть корней.

Алгебраическое решение

Так как выражение от правой части равенства четное и и , выясним вопрос о наличии корней на промежутке . Проверкой устанавливаем, что – корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции и . Так как

и функция непрерывна на числовой прямой, то найдутся такие значения и , что . Поэтому на промежутке уравнение имеет три корня, а на всей числовой прямой – шесть корней.

Ответ: 6 корней.

В данном случае можно решать любым способом, но если количество корней на небольшом промежутке достаточно велико, вычисления могут оказаться громоздкими, и сам метод неэффективным. В этом случае на помощь приходит метод тригонометрической подстановки. Надо заметить, что решить вопрос о количестве корней можно с помощью производной, но в данном случае такое решение мало эффективно, так как затруднительно найти нули производной.

Пример 2. Решить уравнение

.

Если для выше приведенных задач не удается найти нетрадиционный путь решения, то все равно остается вероятность справиться с задачей с помощью стандартных школьных рассуждений, правда, затратив при этом гораздо больше времени. Эта задача лишает такого выбора, так как ее решение другим способом не представляется возможным.

^

Поделим все члены уравнения на 2. Уравнение примет вид

.

Докажем, что все корни данного уравнения по модулю не превосходят единицы. Пусть , тогда . Получили, что при левая часть уравнения по модулю больше единицы, а правая – меньше единицы, что невозможно.

Положим . Уравнение примет вид

.

Условию удовлетворяют три значения

.

Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения.

Ответ: .

^

Приведем пример задания, решить которое без введения тригонометрической подстановки не представляется возможным.

Пример 1. Решить уравнение .

Пусть , тогда уравнение перепишется в виде

.

Введем замену , получим

.

Это уравнение мы уже решали¹. Его корни

.

Два последних значения меньше нуля, поэтому нам подходит только . Перейдем к переменной , а затем к переменной

.

Ответ: .

gendocs.ru

Решение систем линейных алгебраических уравнений общего вида.

В общем случае число уравнений системы pне совпадает с числом неизвестных переменныхn:

Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.

Далее нам потребуется понятие минора матрицы и ранга матрицы, которые даны в статье ранг матрицы: определение, методы нахождения, примеры, решения.

Теорема Кронекера – Капелли.

Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли: для того, чтобы система изpуравнений сnнеизвестными (pможет быть равноn) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть,Rank(A)=Rank(T).

Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.

Пример.

Выясните, имеет ли система линейных уравнений решения.

Решение.

Найдем ранг основной матрицы системы . Воспользуемся методом окаймляющих миноров. Минор второго порядкаотличен от нуля. Переберем окаймляющие его миноры третьего порядка:

Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.

В свою очередь ранг расширенной матрицы равен трем, так как минор третьего порядкаотличен от нуля.

Таким образом, Rang(A) < Rang(T), следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.

Ответ:

система решений не имеет.

Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.

А как же находить решение СЛАУ, если установлена ее совместность?

Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.

Минор наивысшего порядка матрицы А, отличный от нуля, называетсябазисным.

Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы Абазисных миноров может быть несколько, один базисный минор есть всегда.

Для примера рассмотрим матрицу .

Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.

Базисными являются следующие миноры второго порядка, так как они отличны от нуля

Миноры базисными не являются, так как равны нулю.

Теорема о ранге матрицы.

Если ранг матрицы порядка pнаnравенr, то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.

Что нам дает теорема о ранге матрицы?

Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).

В итоге, после отбрасывания излишних уравнений системы, возможны два случая.

1. Если число уравнений rв полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.

Пример.

Решите систему линейных алгебраических уравнений .

Решение.

Ранг основной матрицы системы равен двум, так как минор второго порядкаотличен от нуля. Ранг расширенной матрицытакже равен двум, так как единственный минор третьего порядка равен нулюа рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так какRank(A)=Rank(T)=2.

В качестве базисного минора возьмем . Его образуют коэффициенты первого и второго уравнений:

Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:

Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:

Ответ:

x₁ = 1, x₂ = 2.

2. Если число уравнений rв полученной СЛАУ меньше числа неизвестных переменныхn, то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.

Неизвестные переменные (их rштук), оставшиеся в левых частях уравнений, называютсяосновными.

Неизвестные переменные (их n — rштук), которые оказались в правых частях, называютсясвободными.

Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом rосновных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.

Разберем на примере.

Пример.

Решите систему линейных алгебраических уравнений .

Решение.

Найдем ранг основной матрицы системы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмемa_{1 1} = 1. Начнем поиск ненулевого минора второго порядка, окаймляющего данный минор:

Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:

Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.

Найденный ненулевой минор третьего порядка возьмем в качестве базисного.

Для наглядности покажем элементы, образующие базисный минор:

Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с противоположными знаками в правые части:

Придадим свободным неизвестным переменным x₂иx₅произвольные значения, то есть, примем, где- произвольные числа. При этом СЛАУ примет вид

Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:

Следовательно, .

В ответе не забываем указать свободные неизвестные переменные.

Ответ:

, где — произвольные числа.

Подведем итог.

Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.

Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.

Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.

Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.

К началу страницы

studfiles.net

Специальные методы решения алгебраических уравнений. Решения уравнений высших степеней

Одесское территориальное отделение

Малой академии наук Украины

Секция математики

Специальные методы решения алгебраических уравнений.

Решения уравнений высших степеней

Автор: Касьян Наталья

Ученица 10-М класса

Одесской школы №20

Руководитель:

Касьян Л. Ю.

Научный руководитель

Одесса 2003

Содержание:

1.Определение алгебраического уравнения.

2.История развития науки о решении алгебраических уравнений.

3.Специальные методы решения алгебраических уравнений.

4.Вывод.

5.Список литературы.

Известный немецкий математик Курант писал: «На протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики входило необходимой составной частью в интеллектуальный инвентарь каждого образованного человека». И среди этих знаний было умение решать уравнения.

Уравнение — аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых значения функций равны, — решениями, или корнями, уравнения. О таких значениях неизвестных говорят, что они удовлетворяют данному уравнению.

Совокупность решений данного уравнения зависит от области М значений, допускаемых для неизвестных. Уравнение может не иметь решений в М, тогда оно называется неразрешимым в области М. Если уравнение разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Например, уравнение x⁴ – 4 = 0 неразрешимо в области рациональных чисел, но имеет два решения: x1 = , x2 = — в области действительных чисел и четыре решения: x1 = = , x2 = — , x3 = i, x4 = —i ‑ в области комплексных чисел. Уравнение sinx= = 0 имеет бесконечное множество решений: xk= k, k = 0, 1, 2, …, в области действительных чисел.

Если уравнение имеет решениями все числа области М, то оно называется тождеством в области М.

Два уравнения называются равносильными, если каждое решение одного уравнения является решением другого, и наоборот, причём оба уравнения рассматриваются в одной и той же области.

Процесс разыскания решений уравнения заключается обычно в замене уравнения равносильным. Замена уравнения равносильным основана на применении четырёх аксиом:

1. Если равные величины увеличить на одно и тоже число, то результаты будут равны.

2. Если из равных величин вычесть одно и тоже число, то результаты будут равны.

3. Если равные величины умножить на одно и тоже число, то результаты будут равны.

4. Если равные величины разделить на одно и тоже число, то результаты будут равны.

В некоторых случаях приходится заменять данное уравнение другим, для которого совокупность корней шире, чем у данного уравнения. Поэтому, если при решении уравнения делались действия, могущие привести к появлению посторонних корней, то все полученные корни преобразованного уравнения проверяют подстановкой в исходное уравнение.

Наиболее полно изучены алгебраические уравнения. Их решение было одной из важнейших задач алгебры в 16-17 вв. Уравнения вида = 0, где — многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида

= a0xⁱyⁱ … v^k + a1x¹y^m … vⁿ + asx^py^q … v^r,

где x, y, …, v– переменные, а i, j, …, r– показатели степеней(целые неотрицательные числа). Многочлен от одной переменной записывается так:

= a0xⁿ + a1x^n-1 + … + an-1x + aⁿ.

Например, 3x⁴ – x³ + 2x² + 4x – 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида = 0. Если a00, то n называется степенью уравнения. Например, 2x + 3 = 0 – уравнение первой степени. Уравнения второй степени называются линейными. Уравнение второй степени называются квадратными, а уравнения третьей степени – кубическими. Аналогичные названия имеют и уравнения более высоких степеней.

Решение линейного уравненияax + b = 0 записывается в виде x = — .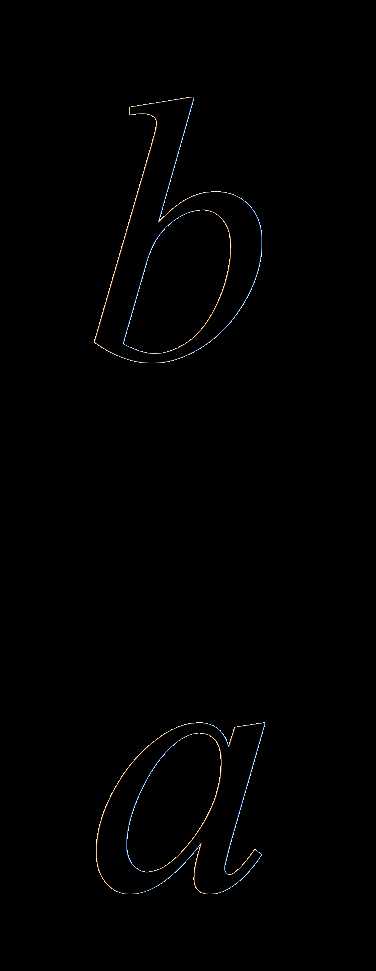

Решения общего квадратного уравнения ax² + bx + c = 0 можно получить с помощью формулы

x=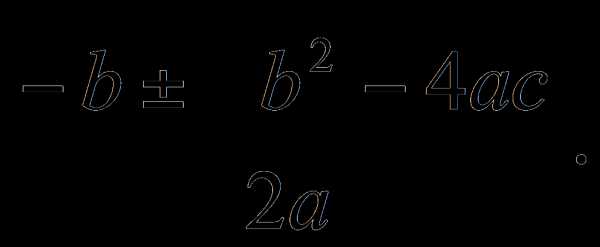

Таким образом, существуют два решения, которые в частном случае могут совпадать.

Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений только третьей и четвёртой степеней. Но и эти формулы сложны и далеко не всегда помогают легко найти корни. Что касается уравнений пятой степени или выше, то для них, как доказал Н. Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удаётся легко решить, факторизуя их левую часть, то есть разлагая её на множители.

Например, уравнение x³ + 1 = 0 можно записать в виде (x + 1)(x² – x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:

x + 1 = 0,

x² – x + 1 = 0.

Таким образом, корни равны x = -1, 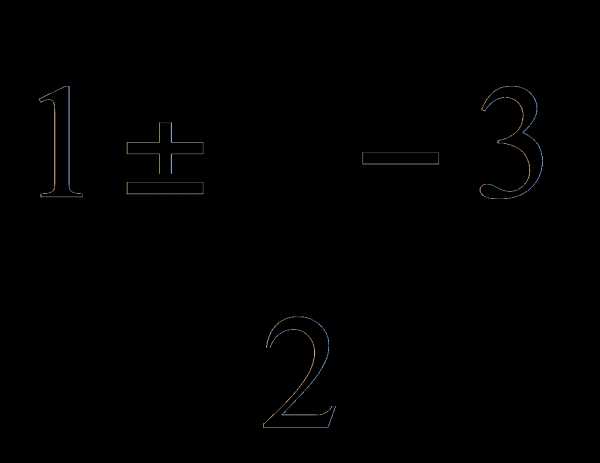, то есть всего три корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твёрдая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.

Уже в древности люди осознали, как важно научиться решать алгебраические уравнения.

К ним сводятся очень многие и очень разнообразные вопросы практики и естествознания (конечно, здесь можно сразу предполагать, что a0 0, так как иначе степень уравнения на самом деле не n, а меньше). Многим, разумеется, приходила в голову заманчивая мысль найти для любо степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах. Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не нашёл! Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n=3 и n=4. История их открытий и даже авторства найденных формул достаточно темны по сей день, и мы не будем здесь выяснять сложные отношения между Ферро, Кардана, Тартальей и Феррари, а изложим лучше математическую суть дела.

Рассмотрим сначала уравнение

а0x³+ a1x²+ a2x + a3 = 0.

Легко проверить, что если мы положим x = y — 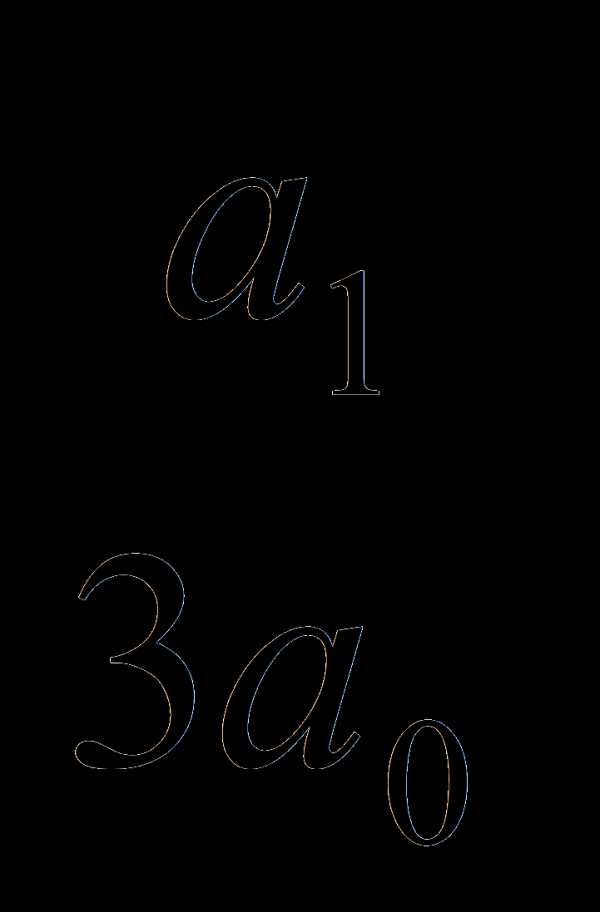, где y – новое неизвестное, то дело сведется к решению уравнения

y³+ py + q = 0,

гдеp,q– новые коэффициенты. Счастливая догадка итальянцев состояла в том , чтобы искать y в виде суммы y = u + v,гдеu,v – два новых неизвестных. Для них уравнение перепишется – после небольшой перегруппировки слагаемых – так:

u³ + v³ + (3uv + p)(u + v0) + q = 0

Так как неизвестных теперь два, на них можно наложить еще какое- нибудь условие – лучше всего

3uv + q = 0,

тогда исходное уравнение примет совсем простой вид

u³ + v³ + q = 0.

Это означает, что сумма кубов u³, v³ должна равняться – q, а их произведение — . Следовательно, сами u³, v³ должны быть корнями квадратного уравнения

t² + qt – = 0,

а для него формула уже известна. В итоге получается формула

y = +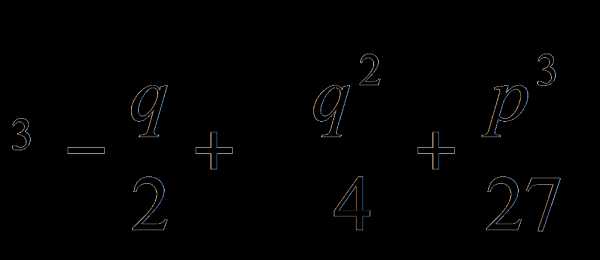

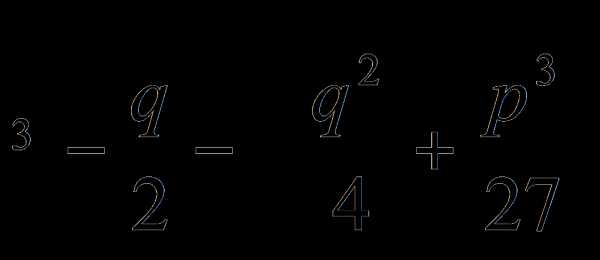
причем из девяти пар значений входящих в нее кубических радикалов надо брать только пары, дающие в произведении –p/3, как вытекает из нашего рассуждения. Исторически за этой формулой закрепилось название формулы Карнадо, хотя вопрос о ее авторстве так до конца и не выяснен.

Для n = 4 формулу открыл Феррари, она выглядит сложнее, но тоже использует только четыре арифметических действия и извлечение радикалов. Вот набросок вывода формулы Феррари. Прежде всего, подобно предыдущему, положим

x = y — , тогда дело сведется к решению уравнения вида

y⁴ + pq² + qy + r = 0.

Дополнив y⁴ до (y² + z)², т.е. прибавив и вычтя в левой части 2zy² + z², где z – вспомогательное неизвестное, получим

(y² + z)² — .

Подберем теперь z так, чтобы квадратный трёхчлен в квадратных скобках оказался полным квадратом. Для этого нужно, чтобы его дискриминант равнялся нулю, т.е. чтобы было

q² — 4(2z – p)(z² – r) = 0.

Можем ли мы решить это уравнение относительно z? Да, можем, так как оно кубическое. Пусть z0 – какой-нибудь его корень (даваемый формулой Кардано) тогда исходное уравнение перепишется в виде

y1 = , y2 = ,

y3 = y4 =

При этом знаки перед радикалами выбирают так, чтобы выполнялось равенство

В 1770-71 гг. знаменитый французкий математик Лагранж (1736-1819) публикует в Мемуарах Берлинской Академии свой мемуар «Мысли над решением алгебраических уравнений», в котором делает критический пересмотр всех решений уравнений 3-й и 4-й степеней, данных его предшественникам.

Исследования Лагранжа дали для последующих алгебраистов весьма удобный аппарат. Кроме того, они указали путь, по которому следовало искать доказательства невозможности общего решения уравнений в радикалах.

Дальнейшим этапом в выяснении проблемы решения уравнений в радикалах послужили работы Руффини (P.Ruffini, 1765-1822) и Абеля (N.-H. Abel, 1802-1829). Руффини (1799) предложил доказательство неразрешимости в радикалах уравнении 5-й степени, коэффициенты которого являются независимыми. Однако его доказательство окончилось неудачей.

Нужен был принципиально новый подход. На этот раз он не заставил себя долго ждать – уже в 1824 году молодой (и в возрасте 27 лет умерший) норвежский математик Нильс Генрик Абель, опираясь на идеи Лагранжа, связанные с перестановками корней уравнения, доказал, что требуемых формул, которые решали бы в радикалах уравнение решали бы в радикалах уравнение общего вида, при n5 действительно не существует. Теорема Абеля дала отрицательны ответ только для уравнений общего вида, т.е. с буквенными коэффициентами а0, а1, …, аn, но, разумеется, многие конкретные уравнения сколь угодно высокой степени вполне могут решаться в радикалах (пример: уравнение x⁹⁰ + 5x⁴⁵ + 7 = 0). Поэтому сразу же встал вопрос о полном решении задачи – нахождении критерия разрешимости уравнений в радикалах, т.е. необходимого и достаточного условия, которое по коэффициентам а0, а1, …, аn любого заданного уравнения позволяло бы судить, решается уравнение в радикалах или нет.

Вопрос о разрешимости уравнений в радикалах был окончательно разобран, во всяком случае, принципиально, в работах Галуа (EvaristeGalois, 1811-1832). За свою короткую жизнь Галуа успел создать теорию, которая до сих пор стоит в фокусе математической мысли. Рассматривая численные уравнения, он установил понятие их группы, т.е. совокупности таких подстановок между их корнями, которые не нарушают рациональных соотношений между ними. Эта группа определяет для каждого уравнения алгебраическую структуру его корней. В частности, уравнение разрешимо в радикалах тогда и только тогда, если его группа принадлежит к числу так называемых разрешимых групп. Таким образом вопрос о разрешимости каждого данного уравнения в радикалах может быть решен при помощи конечного числа действий.

Обратимся теперь к исходному объекту исследования – уравнению

а0xⁿ + a1x^n-1 + … + an = 0,

где а0, а1, …, аn – заданные числа. Еще Гаусс в конце 18 века доказал «основную теорему алгебры», гласящую, что при любых а0, а1, …, аn данное уравнение имеет в поле комплексных чисел n корней, точнее, стоящий в его левой части многочлен может быть разложен на линейные множители

= а0,

где а1 …аn– некоторые комплексные числа (называемые корнями уравнения). Задача состоит в том, чтобы узнать, существуют ли формулы, выражающие корни а1, …, аnчерез коэффициенты а0, а1, …, аnc помощью четырех арифметических действий и извлечения радикалов?

Эварист Галуа доказал, что общее уравнение степени n неразрешимо в радикалах. Шестьдесят страниц, написанных накануне роковой дуэли, явились одним из истоков современной теории групп – основного и наиболее развитого раздела алгебры, изучающего в общем виде глубокую закономерность реального мира – симметрию.

Рассмотрим на примерах некоторые способы решения алгебраических уравнений степени n.

Пример 1. Решить уравнение

.

Разложим левую часть уравнения на множители

Переносим в левую часть и раскладываем полученный многочлен на множители

,

тогда

2x + 2 = 0 или –3x² – 6x + 24 = 0. Решая эти уравнения, получаем корни

x1 = -1, x2 = -4, x3 = 2.

Разложение на множители позволило свести решение кубического уравнения к решению квадратного и линейного уравнений.

Пример 2. Решить уравнение

Разделим обе части уравнения на ( = 0 не является решением уравнения)

,

тогда

.

Пусть тогда 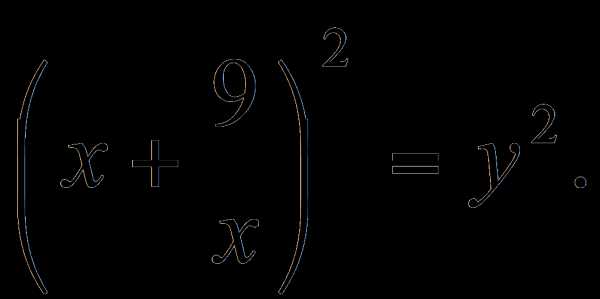Получим уравнение

По теореме Виета корни уравнения: Значит,

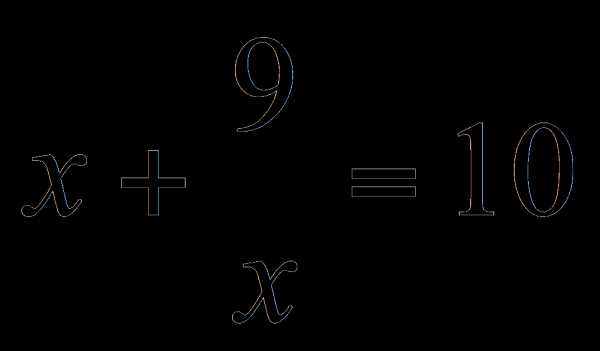или .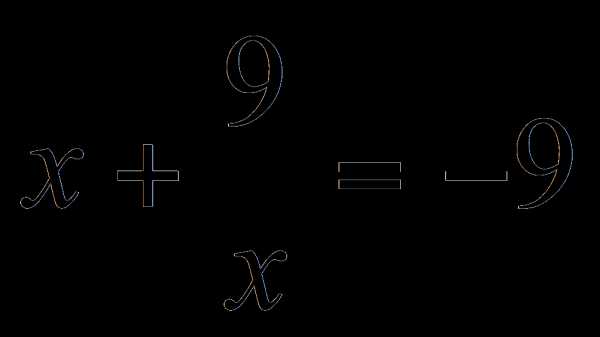

Решая эти уравнения, находим корни

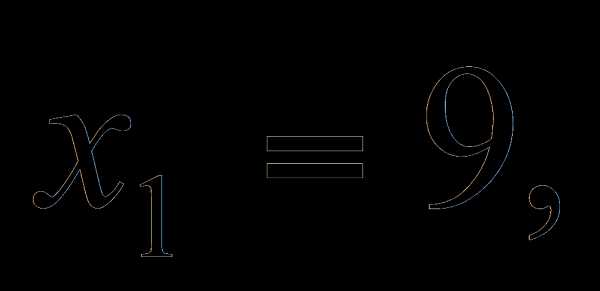
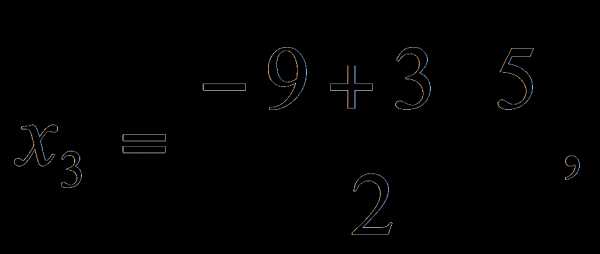
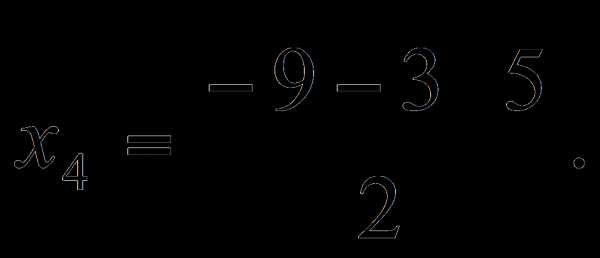
Введение замены позволяет понизить степень уравнения и свести его к решению квадратного уравнения.

Пример 3. Решить уравнение

Заменим это уравнение равносильным ему прибавлением и вычитанием одного и того же выражения .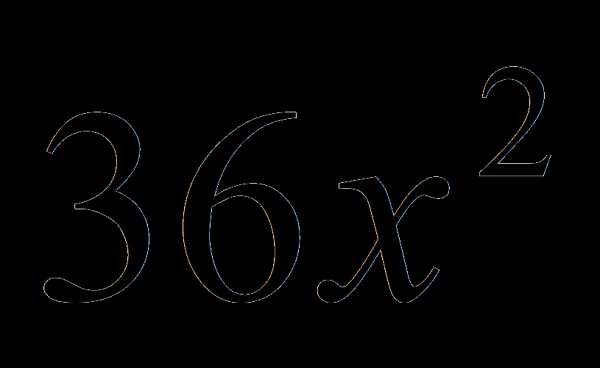

,

Разложим числитель на множители

.

для любого . Сокращая дробь, получим равносильное уравнение

,

корнями которого являются

Это уравнение можно решить другим способом, выполнив деление многочлена на многочлен

Получим Таким образом, выполняя деление многочлена на многочлен можно понизить степень уравнения.

Пример 4. Решить уравнение

Разделив обе части уравнения на (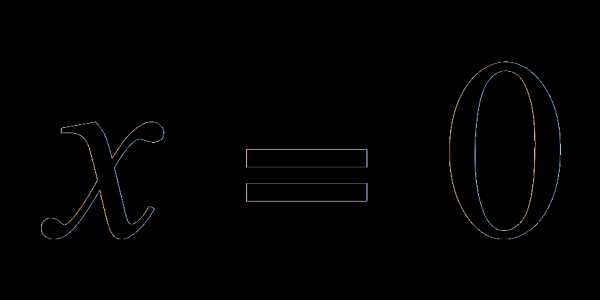 не является решением данного уравнения).

.

Полагая , получим уравнение

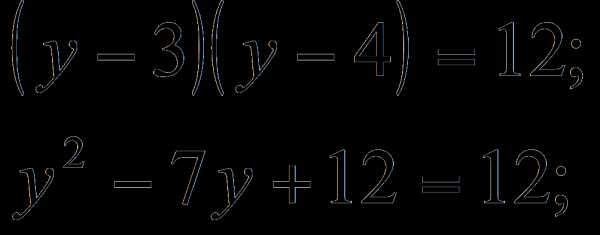
корнями которого являются .

Значит, или 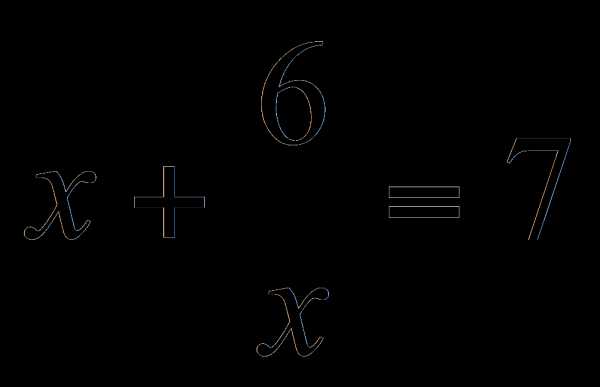. Первое уравнение не имеет решений на множестве R, а корни второго .

Данный пример показывает, что деление обеих частей уравнения на одно и то же выражение с последующим введением замены позволяет понизить степень уравнения.

Пример 5. Решить уравнение

Областью допустимых значений данного уравнения являются все числа, удовлетворяющие условию

Тогда,

Пусть 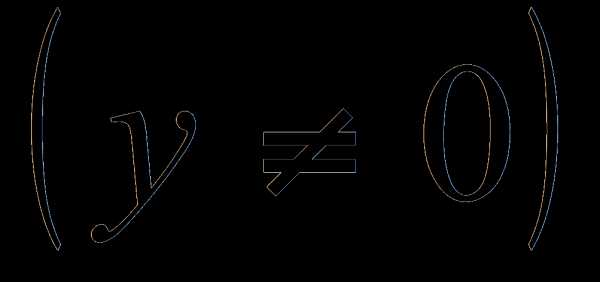, получим уравнение

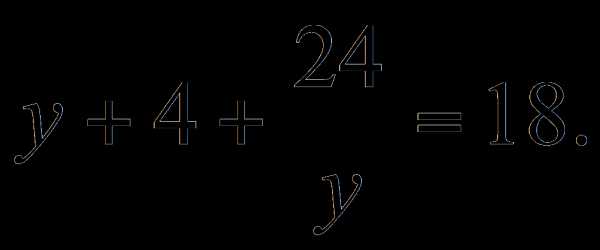
Решая данное дробно-рациональное уравнение, получим корни

Значит,

или

Решениями уравнений являются

Пример 6. Решить уравнение

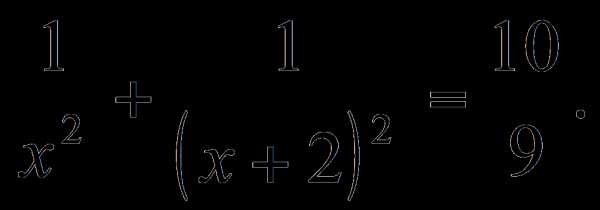
ОДЗ: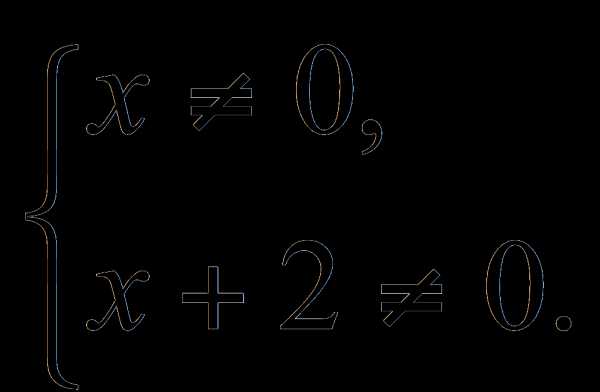

Пусть , тогда Получим уравнение

Выполняя преобразования, данное уравнение приводится к виду

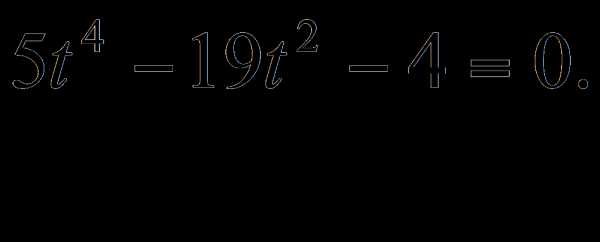
Корни этого уравнения следовательно,

Рассмотренные примеры показывают основные способы решения алгебраических уравнений степени n: разложение многочлена на множители, деление на одно и тоже выражение, введение новой переменной. Все указанные способы позволяют понизить степень уравнения и свести решение данного уравнения к решению квадратного или линейного уравнения.

Истоки алгебры восходят к глубокой древности. Уже около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно – второй степени. С помощью таких уравнения решались разнообразные задачи землемерия, архитектуры и военного дела. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется алгеброй и теорией чисел. Универсальной формулы для нахождения корней алгебраического уравнения n – ой степени нет . В данной работе на конкретных примерах рассмотрели различные способы понижения степени уравнения .

Список использованной литературы:

1.Математическая энциклопедия , том 5 .

2.Тумаркин Л.А. “ История математики “, М., 1975.

3.Кизнер Ф.И. “Основные понятия математики”, М., 1987

4.Смонов А.Я. “Конкурсные задачи по математике”, М., 1991

Контрольная: И.С. Конев Достойное место в плеяде отличившихся земляков занимает известный полководец Великой Отечественной войны дважды Герой Советского Союза Маршал Советского Союза Иван Степанович Конев.

Реферат Программа Mathematics Едва исчезли со страниц журналов восторженные от­зывы на новую версию математического пакета Maple V 4.0 компании Maple Waterloo, как компания Wolfram Research представила не менее интересный продукт — Mathematica 3.0. Она разработана компанией Wolfram Research Inc , ос­нованной известным математиком и физиком Стефаном Вольфрамом, одним из создателей теории сложных систем.

Курсовая: Критерии устойчивости линейных систем В реальной цепи, охваченной обратной связью, всегда имеются реактивные элементы, накапливающие энергию. Даже в усилителе на резисторах имеются такие элементы в виде паразитных емкостей схемы и электронных приборов, переходные конденсаторы, индуктивности проводов и так далее.

Реферат История открытия комплексных чисел “Помимо и даже против воли того или другого математика, мнимые числа снова и снова появляются на выкладках, и лишь постепенно по мере того как обнаруживается польза от их употребления, они получают более и более широкое распространение” Ф. Клейн. ревнегреческие математики считали “настоящими” только натуральные числа.

Курсовая: Метод конечных разностей или метод сеток. Решение бигармонического уравнения методом Зейделя Значительнаое число задач физики и техники приводят к дифференциальным уравнениям в частных прозводных (уравнения математической физики). Установившиеся процессы различной физической природы описываются уравнениями эллиптического типа. Точные решения краевых задач для эллиптических уравнений удаётся получить лишь в частных случаях. Поэтому эти задачи решают в основном приближённо.

Курсовая: Решение систем линейных алгебраических уравнений методом Гаусса и Зейделя Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ.

Курсовая: Разложение рациональной дроби на простейшие. Этот вопрос уже много раз изучен и рассмотрен. Казалось бы, что может быть проще для современного математика, чем разложить рациональную дробь на простейшие, разве что элементарные алгебраические операции. Однако, применение этого метода существенно облегчает жизнь – не будь метода – некоторые задачи было бы очень проблематично решить, а некоторые вообще не решались.

Конспект: Виды квадратных уравнений и способы их решения Обобщить способы решения квадратных уравнений в ходе подготовки к контрольной работе. Активизировать повторение материала в ходе учебного процесса, развивать математические способности учащихся. Вступительное слово учителя: Ребята! Квадратное уравнение – это фундамент, на котором построено огромное здание алгебры. Квадратные уравнения применяются начиная с 8-го класса и до окончания вуза.

nreferat.ru